Our Group organises 3000+ Global Conferenceseries Events every year across USA, Europe & Asia with support from 1000 more scientific Societies and Publishes 700+ Open Access Journals which contains over 50000 eminent personalities, reputed scientists as editorial board members.
Open Access Journals gaining more Readers and Citations
700 Journals and 15,000,000 Readers Each Journal is getting 25,000+ Readers
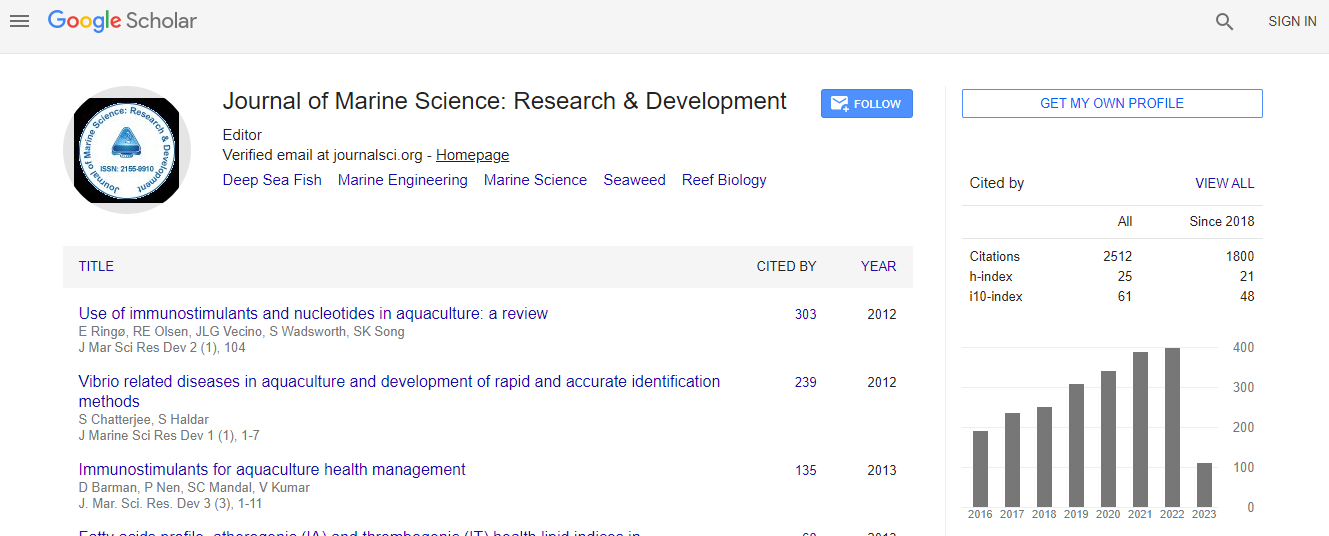
Google Scholar citation report
Citations : 3189
Indexed In
- CAS Source Index (CASSI)
- Index Copernicus
- Google Scholar
- Sherpa Romeo
- Open J Gate
- Genamics JournalSeek
- Academic Keys
- ResearchBible
- Ulrich's Periodicals Directory
- Electronic Journals Library
- RefSeek
- Directory of Research Journal Indexing (DRJI)
- Hamdard University
- EBSCO A-Z
- OCLC- WorldCat
- Scholarsteer
- SWB online catalog
- Virtual Library of Biology (vifabio)
- Publons
Useful Links
Recommended Journals
Related Subjects
Share This Page
Numerical modeling of tsunami propagation with improved dispersion effects
International Conference on Oceanography & Natural Disasters
Taemin Ha, Jaeseol Shim and Jaeseon Yoo
Posters: J Marine Sci Res Dev

 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi