| Research Article |
Open Access |
|
| Rajeev Singh Kushwaha* and Mohan Singh Kushwaha |
| Department of Applied Mathematics, Institute of Technology, Banaras Hindu University, Varanasi-221005, India |
| *Corresponding author: |
Rajeev Singh Kushwaha
Department of Applied Mathematics
Institute of Technology
Banaras Hindu University
Varanasi-221005, India
E-mail: rajeev.apm@itbhu.ac.in |
|
| |
| Received July 15, 2012; Published October 01, 2012 |
| |
| Citation: Kushwaha RS, Kushwaha MS (2012) Adomian Decomposition Method for a Moving Boundary Problem with Variable Latent Heat. 1:401. doi:10.4172/scientificreports.401 |
| |
| Copyright: © 2012 Kushwaha RS, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. |
| |
| Abstract |
| |
| In this article, an approximate analytical solution of a moving boundary problem with variable latent heat by Adomian decomposition method is presented. The results of sediment height and shoreline movement are compared with a published analytical solution and are in good agreement. A brief sensitivity analysis is also performed. |
| |
| Keywords |
| |
| Moving boundary problem; Adomian decomposition method; Sediment transport; Shoreline problem |
| |
| Nomenclature |
| |
| x - space variable, [m]; t - time; b - height of the earth’s crust (basement) above datum, [m]; z(t) - ocean level above datum, [m]; s(t) - shoreline position, [m]; u(t) - position of intersection between offshore sediment wedge and basement, [m]; q - prescribed sediment line flux [m3m-1t-1]; ν - diffusion coefficient, [m2t-1]; Greek letters; h - height of sediment above datum, [m]; a - slope of off-shore sediment wedge; β - slope of basement; g - a constant (=ab/(a-b)) |
| |
| Introduction |
| |
| A problem related to the shoreline movement in a sedimentary ocean basin due to a sediment line flux, tectonic subsidence of the earth’s crust, and sea level change, is a moving boundary problem with variable latent heat. In 2000, Swenson et al. [1] presented a mathematical model for movement of shoreline in a sedimentary basin (shoreline model) by utilizing an analogy with one-phase melting problem. Voller et al. [2] presented an analytical solution for a Stefan problem with variable latent heat (a limit case of the shoreline model) which is based on a similarity variable. Capart et al. [3] discussed some mathematical solutions for several sedimentary problems featuring semi-infinite alluvial channels evolving under diffusional sediment transport. Later, Voller et al. [4] used enthalpy method to solve a novel moving boundary problem related to shoreline movement in a sedimentary basin. In 2009, Rajeev et al. [5] presented a numerical method for a moving boundary problem with variable latent heat. Recently, Rajeev [6] successfully applied homotopy perturbation method to solve a Stefan problem with variable latent heat and the results are compared with the results of Voller et al. [2]. |
| |
| Exact solutions of moving boundary problems are difficult to obtain except for some special cases [7,8]. The difficulties arise due to its nonlinearity nature and unknown boundary on moving interface. Hence, many approximate analytical methods have been used to solve the moving boundary problems. The approximate analytical approach taken in this article is Adomian decomposition method (ADM) developed by Adomian [9,10]. In the literature, many researchers [11-13] applied this method to solve various types of non-linear problems. Das and Rajeev [14] used variational iteration method and Adomian decomposition method to solve time-fractional diffusion equation with a moving boundary condition which is related to the diffusional release of a solute from a polymer matrix in which the initial loading is higher/lower than the solubility. |
| |
| The objective of this article is to find an approximate analytical solution of a moving boundary problem with variable latent heat by using Adomian decomposition method. The obtained results of sediment height and shoreline movement are compared with the existing analytical solution given by Voller et al. [2]. The dependence of shoreline movement on sediment line flux and constant γ is also discussed. |
| |
| Mathematical Model |
| |
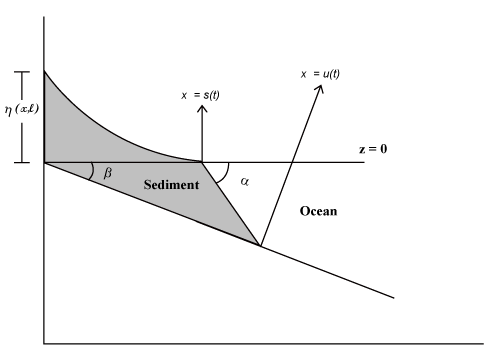
| In this section, we consider a mathematical model of Voller et al. [2] which is a limit case of the shoreline model given by Swenson et al. [1]. The limit case of shoreline model involves a shoreline problem with a fixed line flux, a constant ocean level (z=0), no tectonic subsidence of the earth’s crust, and a constant sloping basement α>β. This scenario is a reasonable approximation for some modern continental margins. A schematic cross section of such a basin indicating the variables is revealed in figure 1 [2,6]. The governing equation and posed conditions are as follow: |
| |
|
|
Figure 1: A schematic cross section of a basin with no tectonic subsidence and sea level change. |
|
| |
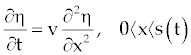 (1) (1) |
| |
| With initial and boundary conditions |
| |
 (2) (2) |
| |
and  (3) (3) |
| |
Where  is height of sediment above datum, υ is a diffusion coefficient, q(t) is prescribed sediment line flux and s(t) is the moving interface. is height of sediment above datum, υ is a diffusion coefficient, q(t) is prescribed sediment line flux and s(t) is the moving interface. |
| |
| The additional conditions on the moving interface are |
| |
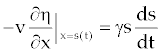 (4) (4) |
| |
| And s(0)=0 (5) |
| |
Where 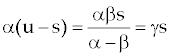 which is latent heat term that is function of space and λ is a constant. which is latent heat term that is function of space and λ is a constant. |
| |
| Solution of the Problem by ADM |
| |
| We first write the equation (1) in an operator form |
| |
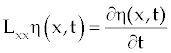 (6) (6) |
| |
Where 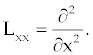 |
| |
| Assuming that the inverse operator Lxx-1 exists and |
| |
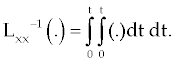 |
| |
| Applying the inverse operator Lxx-1 on both side of the equation (6) |
| |
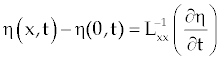 (7) (7) |
| |
| Choosing the initial approximations of η(x,t) and s(t) as given in [14] |
| |
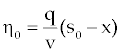 |
| |
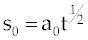 |
| |
Where 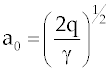 |
| |
| According to the Adomian decomposition method [9-11], decomposing the unknown function η(x,t) as follows: |
| |
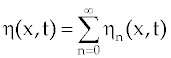 (8) (8) |
| |
Where the components  are defined as are defined as |
| |
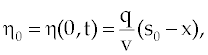 |
| |
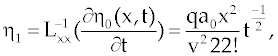 |
| |
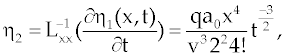 |
| |
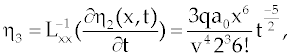 |
| |
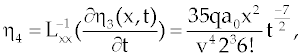 |
| |
| |
| According to the Adomian decomposition method [9-11], decomposing the unknown |
| |
Thus, 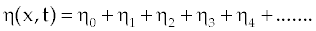 |
| |
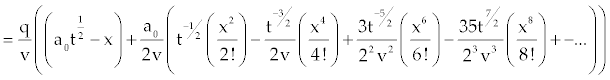 |
| (9) |
| which give height of the sediment above the datum. |
| |
| Now, using (9) and writing the interface condition (4) in operator form |
| |
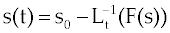 (10) (10) |
| |
Where initial approximation 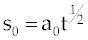 |
| |
and 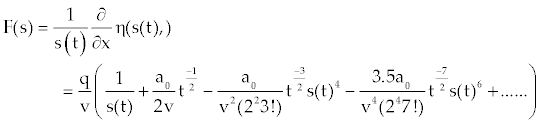 |
| |
| Accordingly [9], decomposing s(t) as |
| |
 (11) (11) |
| |
| Using (10) and (11), we have |
| |
 (12) (12) |
| |
| Where An are so-called Adomian polynomials for non-linear terms and defined as |
| |
 (13) (13) |
| |
and so on. The components of  , can be completely determined as , can be completely determined as |
| |
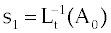 |
| |
Where 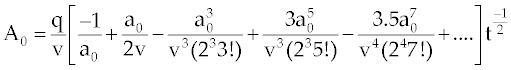 |
| |
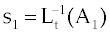 |
| |
| Where |
| |
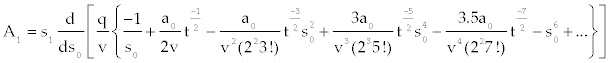 |
| |
| and so on. Therefore, approximate analytical solution of s(t) is given by |
| |
| s(t)=s0+s1+s2+…………. |
| |
| Numerical Comparison and Discussion |
| |
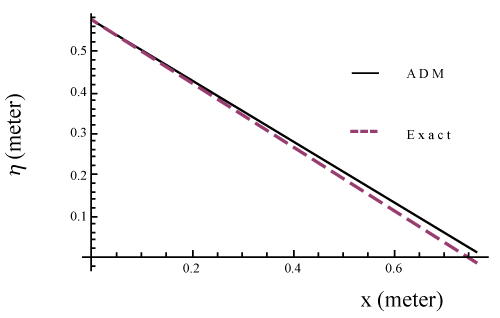
| In this section, all the numerical results for height of sediment h (x, t) and shoreline position s(t) are calculated for the fixed value of slope of basement (β=1.5), slope of offshore sediment (α=1.7) and diffusion coefficient (v=2.0m 2t -1) by using MATHEMATICA software . For accuracy, the approximate solutions by ADM are compared with the existing results of Voller et al. [2] and depicted through figures 2-5. It is observed that |
| |
|
|
Figure 2: Plot of η(x, t) vs. x for q=0.5 m3m-1t-1. |
|
| |
 (14) (14) |
| |
 (15) (15) |
| |
| where λ is the root of the following equation |
| |
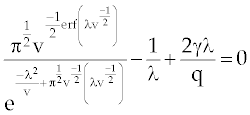 (16) (16) |
| |
| are exact solutions to the equations (1)-(5). |
| |
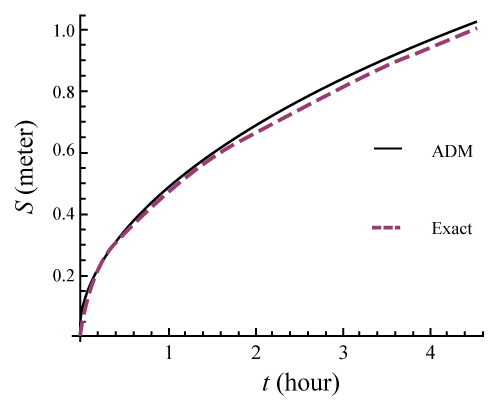
| Figures 2 and 3 represent the dependence of height of sediment h (x,t) on x at v=2.0m2t-1 for q=0.5 and q=1.5, respectively. Figures 4 and 5 describe the movement of shoreline position at v=2.0m2t-1 for q=0.5 and q=1.5, respectively. From the figures 2-5, it is observed that the approximate solutions obtained by ADM are sufficiently accurate with the exact results of Voller et al. [2]. |
| |
|
|
Figure 3: Plot of η(x, t) vs. x for z=1.5 m3m-1t-1. |
|
| |
|
|
Figure 4: Plot of s(t) vs. t for q=0.5 m3m-1t-1. |
|
| |
|
|
Figure 5: Plot of s(t) vs. t for q=1.5 m3m-1t-1. |
|
| |
| It can be seen from figure 6 that for the fixed values of a=1.7, b=1.5, v=2.0 m2t-1, the movement of the shoreline position increases towards sea side as the sediment line flux q increases (q = 0.5, 1.0, 2.0). This result is in good agreement with the result of Rajeev et al [5]. |
| |
|
|
Figure 6: Plot of s(t) vs. t for v=2.0 m2t-1. |
|
| |
| It is observed from figure 7 that for the fixed values of a=1.7, b=1.5, v=2.0 m2t-1, if the value of g increases, the shoreline movement deceases. In this case, sediments will be deposited towards the land side which causes the increase in thickness of the sediments and there will be least shifting of the contact point towards the land side. Due to this, the sedimentation process becomes slower. |
| |
|
|
Figure 7: Plot of s(t) vs. t for q=0.5 and v=20. |
|
| |
| Conclusion |
| |
| The Adomian decomposition method is successfully applied to find explicit expressions of height of sediment and shoreline position of a moving boundary problem with variable latent heat. From present study, it is observed that sedimentation process and shoreline movement become faster as the value of sediment line flux increases. But, sedimentation process as well as shoreline movement become slower, if the values of g increases. It is seen that ADM is a powerful and sufficiently accurate method for finding the solution of nonlinear problems of scientific and engineering. Moreover, this is an efficient and straight forward technique for solving moving boundary problems. The author believes that the procedure as described in the present study will be beneficial to researcher working in this field. |
| |
| |
| References |
| |
- Swenson JB, Voller VR, Paola C, Parker G, Marr JG (2000) Fluvio-deltaic Sedimentation: A generalized Stefan Problem. Eur J Appl Math 11: 433-452.
- Voller VR, Swenson JB, Paola C (2004) An Analytic Solution for a Stefan Problem with Variable Latent Heat. Int J Heat Mass Transf 47: 5387-5390.
- Capart H, Bellal M, Young DL (2007) Self-similar Evolution of Semi-infinite Alluvial Channels with Moving Boundaries. J Sediment Res 77: 13-22.
- Voller VR, Swenson JB, Kim W, Paola C (2006) An Enthalpy Method for Moving Boundary Problems on the Earth’s Surface. Int J Numerical Methods for Heat & Fluid Flow 16: 641-654.
- Rajeev, Rai KN, Das S (2009) Numerical Solution of a Moving-Boundary Problem with Variable Latent Heat. Int J Heat Mass Transf 52: 1913-1917.
- Rajeev (2012) Homotopy Perturbation Method for a Stefan Problem with Variable Latent Heat. Thermal Science.
- Crank J (1987) Free and Moving Boundary Problem. Oxford University Press, USA.
- Carslaw HS, Jaeger JC (1986) Conduction of Heat in Solids. Clarendon Press, Oxford University, USA.
- Adomian G (1988) A Review of the Decomposition Method in Applied Mathematics. J Math Anal Appl 135: 501-544.
- Adomian G (1993) Solving Frontier Problems of Physics: The Decomposition Method. Springer Publication, USA.
- Adomian G (1998) Solutions of Nonlinear PDE. Appl Math Lett 11: 121-123.
- Wazwaz AM (2000) The Decomposition Method for Solving the Diffusion Equation Subject to the Classification of Mass. Int J Appl Math 3: 25-34.
- Wazwaz AM (2007) A Comparison between the Variational Iteration Method and Adomian Decomposition Method. J Comput Appl Math 207: 129-136.
- Das S, Rajeev (2010) Solution of Fractional Diffusion Equation with a Moving Boundary Condition by Variational Iteration Method and Adomian Decomposition Method. Zeitschrift für Naturforschung 65a: 793-799.
|
| |
| |
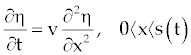 (1)
(1) (2)
(2)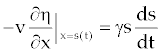 (4)
(4)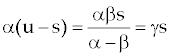 which is latent heat term that is function of space and λ is a constant.
which is latent heat term that is function of space and λ is a constant.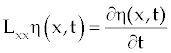 (6)
(6)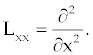
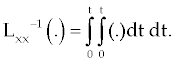
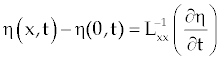 (7)
(7)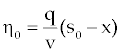
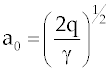
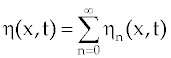 (8)
(8)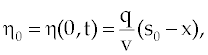
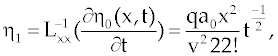
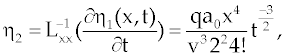
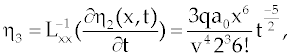
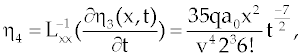
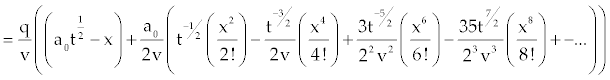
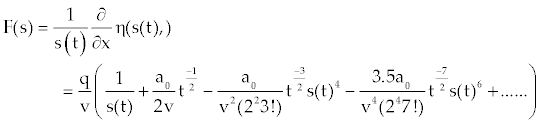
 (11)
(11) (12)
(12) (13)
(13)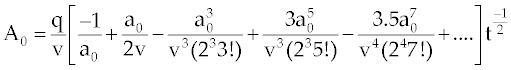
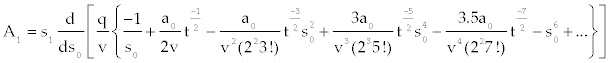
 (14)
(14)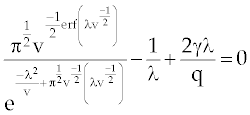 (16)
(16)