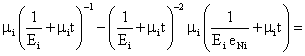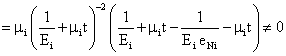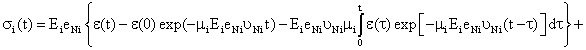| Research Article |
Open Access |
|
| ÃÅÃÂ Ramazanov1*, ÃÅS Aslanov2 |
| 1Baku State University, Baku, Azerbaijan |
| 2Azerbaijan Technical University, Baku, Azerbaijan |
| *Corresponding authors: |
M.A. Ramazanov
Baku State University, Baku, Azerbaijan
E-mail: mamed_r50@mail.ru |
|
| |
| Received March 16, 2012; Published July 30, 2012 |
| |
| Citation: Ramazanov MA, Aslanov ?S (2012) Synthesis of the Maxwell Model Based on Nanoparticles. 1: 233. doi:10.4172/scientificreports.233 |
| |
| Copyright: © 2012 Ramazanov MA, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. |
| |
| Abstract |
| |
| The paper studies the viscoelastic fluid described by the synthesized Maxwell model. Assuming the interaction of atoms of the body with embedded nanoparticles leads to a change in model parameters. It is shown that with the addition of nanoparticles with a specific property, it can change the value of the deformation points of a viscoelastic fluid. |
| |
| Keywords |
| |
| Viscoelastic fluid; The Maxwell model; Nanoparticle; Value of the deformation points. |
| |
| Introduction |
| |
| The establishment of efficient technologies based on nanotechnology in areas such as military equipment, the oil industry, automotive industry, shipbuilding, construction, aviation, etc. is highly appreciated. These technologies are connected with increasing of oil recovery factor of deposits with highly viscous oil. The solution of the problem leads to increasing of volume of hardly extracted oil. There are a lot of researches on this direction. |
| |
| Among them is the technology based on application of nanoparticles [1-5]. As it was noted in [2], the efficiency of suggested technology is connected with change of physical mechanical properties of oil containing systems. Taking into account that such systems are described by viscous elastic or viscous plastic models, there is a problem of describing of models with taking into consideration the interactions on atomic or molecular level. For describing such system without taking into account of nanoparticles was suggested the model of viscous elastic body, that is studied in detail in [7]. For studying of nanoparticles influence it is reasonable to upgrade the existing models of viscous elastic bodies, by bringing in the parameters, characterized the properties of nanosized particles. The building of the models of viscous elastic fluids, containing nanoparticles is the one of urgent problems of nanotechnology. |
| |
| At the present work is considered the generalized model of viscous elastic fluids [4,7]. It is based on generalization of simple Maxwell model. |
| |
| Setting of the problem |
| |
| Let us consider the generalized model of viscous elastic fluids that is known as generalized model of Maxwell (Figure 1). It consists of n parallel jointed simple Maxwell models. The simple Maxwell model consists of successively jointed viscous and elastic elements (Figure 1). |
| |
|
|
Figure 1: Generalized Maxwell model |
|
| |
As it was mentioned above the generalized Maxwell model consists of parallel jointed i -numbered Maxwell models. The simple i - numbered Maxwell model is described by successively jointed i - numbered elastic element, for which the following correlation is acceptable σ1i = Ei ε1i and i - numbered elastic element for which the following correlation is acceptable 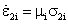 |
| |
| There are following designations: index «1» and «2» correlate to elastic and viscous elements of i - numbered model conformably, σ1i, σ2i and ε1i , ε2i strain and deformation of each above mentioned elements, Ei - elasticity modulus, μi - viscosity coefficient of corresponded i - numbered element of simple Maxwell model. The dot demonstrates the derivative on time t. |
| |
Let us accept, σ1i = σ2i and designate it σi, i.õ. σ1i = σ2i ≡ σi at consecutive joint in i - numbered simple Maxwell model. Then for generalized model where σ - strain, applied to body, n - number of simple models (Figure 1). Then the deformation of i - numbered Maxwell model is defined by correlation where σ - strain, applied to body, n - number of simple models (Figure 1). Then the deformation of i - numbered Maxwell model is defined by correlation |
| |
| ε1i + ε2i = εi (1) |
| |
| Where εi - general deformation of i - numbered Maxwell model (Figure 1). Correlation (1) follows from condition of consecutive joint of elastic and viscous elements. It should be noted that parallel joint of elastic and viscous elements the deformation of generalized model is general for all these elements, i.õ. εi = ε.. |
| |
| Then accepting Ei = const, μi = const, ε is: |
| |
 (2) (2) |
| |
| This equation is solved at following initial condition: |
| |
 (3) (3) |
| |
| It means that in start moment the viscous element ‘does not work. |
| |
| The decision of equation (2) is presented as follow: |
| |
 (4) (4) |
| |
| Or integrating by parts |
| |
 (5) (5) |
| |
| Where C0i - the constant of integrating. |
| |
| Then the decision of equation (2), satisfied to initial condition (3), is as follow: |
| |
 (6) (6) |
| |
| Based on accepted equation and dependence σ from σi we get: |
| |
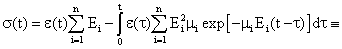  (7) (7) |
| |
| óôõ E0 - generalized modulus of elasticity, Ãâ(t-τ) - generalized nuclei of fluidity. |
| |
| This expression is used to find dependence of ε and σ. Usually these correlations describe the behavior of viscous elastic “liquid” environments [7]. Some nanotechnological approaches in oil extraction suggest supercharging nanoparticles in oil layer. It leads to change of oil characteristics and consequently to change of parameters describing viscous elastic fluids Assume that structure of initial model does not change by adding nanoparticles i.e. the initial model is generalizing of Maxwell model but with other parameters. Let us define the characteristics of this model. The analysis of the results reveals that adding of nanoparticles leads to change of both elastic and viscous characteristics of the model [4,5]. For its definition let us build the model that makes possible to describe these changes with some approximation. |
| |
| To solve the problem |
| |
| Assume that elastic element of Maxwell model can be presented as one-dimensional “chain” of atoms, interacting with each other. Such representation is characteristic for polymer molecules. |
| |
| Let us assume that each embedded nanoparticle takes interstitial place between atoms (though it is possible embedding of more than one nanoparticles). By this the structure of elastic element does not change: it remains as a rectilinear “chain”. It followed from the assumption of preservation of Maxwell model by the adition of nanoparticles. Let us assume that particles interact only with neighboring particles. Then without taking into account of nanoparticles it is follow: |
| |
 ; ; |
| |
where Fi(a) - force of atomic interaction, a - bond length between atoms after deformation, a0 - before deformation, - elasticity coefficient, Rx - characteristic size of the square of diametrical section of atom exposed to force, prim – shows the derivative on coordinate, σi and εi - strain and deformation in each of above mentioned elements. - elasticity coefficient, Rx - characteristic size of the square of diametrical section of atom exposed to force, prim – shows the derivative on coordinate, σi and εi - strain and deformation in each of above mentioned elements. |
| |
| Then we get the following correlations: |
| |
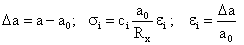 |
| |
| In case with the consideration of nanoparticle: |
| |
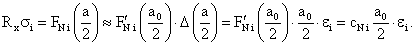 |
| |
| The correlation of elasticity of the “chain” with consideration of nanoparticles. |
| |
 (8) (8) |
| |
| Where «i» and «N» - means that this quantity relates to i - numbered model of Maxwell and nanoparticle. It is assumed that nanoparticle is placed between atoms, in the middle of the “chain”. It should be noted that this location is energetically more profitable. |
| |
| The viscous element of i - numbered Maxwell model is presented like cylinder, filled by viscous fluid, pressed by piston. Let us assume that nanoparticles are in viscous fluid, it leads to preserving a kind of Maxwell model element. In this case the influence of nanoparticles is analogous to the influence of solid particles in the viscous fluid. The influence of nanoparticles can appear in different ways: increasing friction force on cylinder walls, change of characteristic properties of fluids, combination of these effects. Besides this, it is possible the absence of influence. The choice of effect depends on interrelation of physical chemical properties of fluid and nanoparticles as well as interaction condition. All the above mentioned influences of nanoparticles for considered model can be came to change of viscosity coefficient, i.e. the quantity μN i should be introduced. Proceeding from physic effect it follows μN i ≤ μ i. Indeed let us consider the first variant. Assume that introduction of nanoparticles in the fluid leads to increasing of friction force of fluid. At tension of the piston with same force the speed of movement decrease due to the friction, i.e. |
| |
 . . |
| |
| The reduced inequality is as folows. |
| |
| Then based on correlation (1), definite equation of Maxwell model with consideration of nanoparticles is: |
| |
 (9) (9) |
| |
| There are the next designations: |
| |
 ; ; ; ; 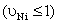 . . |
| |
| The solving of equation (9) by analogues with (4) is: |
| |
 (10) (10) |
| |
| or |
| |
|
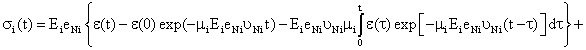
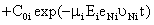
|
| |
| Because the essence of initial condition does not change, then equation (10), satisfied to initial condition (3), is as follows: |
| |
 (11) (11) |
| |
| Taking into consideration that common strain σ is equal to the sum of strains σi, basing on (11), we get: |
| |
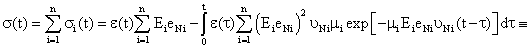
 (12) (12) |
| |
| |
| Where E0N - generalized elasticity modulus,ÃâN (t-τ) - generalized nuclei of fluidity with consideration of nanoparticles. |
| |
| At the constant on time tension load, i.õ. in case σi (t) = const = σi (0) > 0 expression (11) is transformed as: |
| |
 (13) (13) |
| |
| Based on obtained equation and dependence of σ(0) from σi (0), we get: |
| |
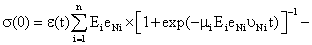
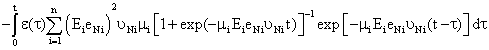 |
| |
| So, the generalized Maxwell model has been shown that the presence of nanoparticles in constituent elements leads to change of model parameters. The character of these changes and its values is described in the frame of assuming of nanoparticles interactions with elastic element atoms and viscous fluid. |
| |
| Let us analyze the influence of nanoparticles in the simple case, when υN i = μi (υN i = 1). Then definition equation is as follow: |
| |
 (14) (14) |
| |
| Define the relation of deformations, before and after introduction of nanoparticles. It is equal |
| |
 (15) (15) |
| |
| The limit values of deformation relations is as follow |
| |
 ; ; . . |
| |
| The stationary dot of relation is defined from the solving the following equation: |
| |
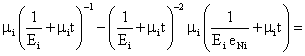 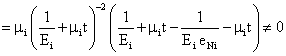 |
| |
| It is not difficult to show that the root of this equation does not exist, i.õ. the relation of deformations is monotonous function. And at eN i > 1, this function monotonously increases, and at eN i < 1 - monotonously decreases. |
| |
| So if the elastic bonds of nanoparticles satisfy to following inequality eN i < 1, i.õ. cN i < 2ci, then addition of nanoparticles in viscous elastic fluid leads to increasing of deformation. In controversial case, i.õ. if cN i > 2ci, then addition of nanoparticles leads to decreasing of deformation. So, for the model of viscous elastic fluid of Maxwell, it is possible to change the value of deformation by the addition of definite nanoparticles, i.õ. to change the properties of the model. |
| |
| Conclusion |
| |
| The work is about the generalization of the model of theory of viscous elasticity with consideration of nanoparticles. Considering that the view of model is preserved, for generalized Maxwell model is reduced the essential correlations. For this model is shown the influence of nanoparticles on mechanical properties. |
| |
| |
| References |
| |
- Ramazanov ÃÅÃÂ, Ali-zade RÃÂ, Agakishieva PB (2010) Structure and magnetic
properties of nanocomposites on the basis PE+Fe3O4 ø PVDF+ Fe3O4. Digest
Journal of Nanomaterials and Biostructures 5: 727-733.
- Magerramov AM, Ramazanov MA, Mustafaeva Akh (2010) Structure and
Properties of Nanocomposites based on Zinc Sulfide and Poly(Vinylidene
Fluoride). Russian Journal of Applied Chemistry 83: 1324-1327.
- Alizadeh AN (2010) Reports of National Academy of Sciences of Azerbaijan.
66: 5-34.
- Ramazanov MA, Aslanov MS (2011) VI International Symposium: "Fullerenes
and Nanostructures in Condensed Matter".
- Ramazanov MA, Aslanov MS (2010) Proceedings of I International Scientific
Conference "Nanotechnology and its application in engineering", Baku,
December 15-16.
- Pomogailo AD, Rosenberg AS, Uflyand IE (2000) Metal Nanoparticles in
Polymers. Moscow.
- Christensen RM (1974) Introduction to the theory of viscoelasticity.
|
| |
| |
 (4)
(4)  (5)
(5)  (6)
(6)  (10)
(10) (11)
(11) (13)
(13)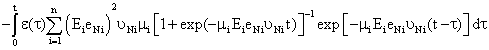
 (14)
(14) (15)
(15)  ;
;