Topological Phenomenology of Space Architecture as Roots of Infinity

Magyar P^*

Department of Architecture, Kansas State University, USA

*Corresponding Author:

Magyar P
Department of Architecture
Kansas State University, USA
Tel: 1785-532-6011
E-mail: pmagyar@ksu.edu

Received Date: July 08, 2015 Accepted Date: July 19, 2015 Published Date: July 29, 2015

Citation: Magyar P (2015) Topological Phenomenology of Space Architecture as Roots of Infinity. J Archit Eng Tech 4:148. doi:10.4172/2168-9717.1000148

Copyright: © 2015 Magyar P. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Visit for more related articles at Journal of Architectural Engineering Technology

Introduction

Ideas mature, but interestingly enough, they never get old! It is also notable, how are they born. In my case, two elements brought them forward: one question, and an admirably unique surrounding. Let me begin with the latter one. In the beginning of my so-called mid-career, I had the great opportunity, to live, practice and teach in Africa! For almost four years, we lived in Zaria, an ancient Nigerian town, with a modern university outside its medieval walls. It is impossible to list all the enlightening influences one encounters in a strange, yet deep rooted culture! Worthy of at least another article, the muslim socio-religious ideas, the abundance of the reddish laterite-mud, and the inherent human ability to build, produced an incredibly homogeneous physical and ideological environment. Addressing here only the physical one, it was almost dream-like uniformity between the ground, the walls and roofs of the self-built villages! So no wonder, when in the process of designing a modern, but traditional house to the city of Ife, another old town, to the question, what is the condition of spatial continuity, the subconsciously preprogrammed answer was: surface continuity! This obvious recognition of an element, visually dominantly present everywhere, fermented further meditations on that subject and the idea of the "Spaceprint" was born.

Returning to the subject of this article, Phenomenology comes from the Greek 'phainomenon'=that which appears, and 'logos'=study. "(It) is the philosophical study of the structures of experience and consciousness" – according to Wikipedia.

We will stop here, and I will explain the willful marriage, what I forced 'topology' and 'phenomenology' into. Jean Piaget, the late Swiss philosopher and clinical psychiatrist, after hundreds of actual tests with children of very young age, in his book: The Child's Perception of Space, made the statement, that our psyche, our consciousness, is organized by topological principles. Also, Maurice Merleu Ponty, one of the father of phenomenology, wrote this in his book, "The Primacy of Perception": "if we are seeking to form an idea of, or to understand the essence of, a spatial figure...we must first perceive it. Then we will imagine all the aspects contained in the figure as changed. That which cannot be varied without the object itself disappearing is the essence." This is a very important, maybe unintentionally topological statement. So, good bye phenomenology, hello topology Paul Valery, in “Eupalinos ou l’Architecte” wrote: "Music and Architecture force us, to transcend in thought that which they would seem, in reality, to imply; they rest in the middle of this world like monuments of another world; or like scattered instances of structure and time which are not products of human beings, but of basic forms and laws."

Doing a competition for ‘A House for Johann Sebastian Bach”, I made the following assumption: Music can be perceived as a "knot" on the infinite line of time, while architecture is a "spatial-loop (-system) " on the infinite surface of the Earth, which separates space and nonspace.

So, the "knotters" and the "loopers" are doing very similar service to mankind: to bring forth, what is un-hearable and in-visible for most everybody, except for those, whose existence is rewarded and burdened with this self-imposed duty [1].

Again, knots and loops are very much in the language of topology, so let us see, what they mean for our investigation. Topology is the youngest but fast-developing and one of the most important aspects of Mathematics and Geometry. In my studies, at this time, I apply only one simplified branch of topology, the visual topology. These kind of topological transformations do not conserve the proportions, measurements, and directions; only the continuity and neighborhood relations of the surface are to be un-changed. "Rubber-sheet-geometry", because it deals with that property that an object retains under deformation, specifically bending, stretching and squeezing, but not breaking or tearing. Since topology by its nature is not scale-specific, topological transformations can be applied from micro to macro scale (e.g. industrial design, urban design).

We can then continue with the following assertions: If we free the boundary conditions from the measurable (metric) restrictions while applying topological transformations to them, we produce the "Topologically Equivalent Model" and we can call it "General Spaceprint" (the "essence" of M. Merleau-Ponty). Every "Particular Spaceprint" is reducible to one "General Spaceprint" but from one "General Spaceprint" unlimited number of "Particular Spaceprints" can be generated. Based on Jean Piaget's research, I forward the hypothesis: there might exist a correlation between a so called Biologically Coded Formal Preference and the similarity of the General and Particular Spaceprints, which similarity I call "Topological Isomorphy”

According to general practice in architecture, intentionally or unintentionally, the shapes of the “Spaceprints” are conceived and articulated by design, and realized through construction. Therefore architecture as a design process is the planning of, and as a product is the execution of, appropriate changes in the surfaces or “Spaceprints” [2].

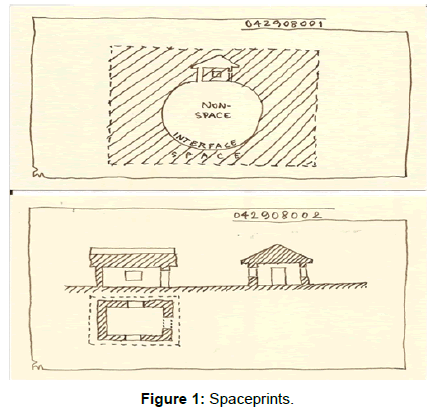
Let us now look at the drawings. On our diagrams, the upper surface represent the stretched, flattened surface of the Earth, including the similarly handled external surfaces of buildings. The “tubes” stand for the openings (windows, doors), connecting the internal surfaces of the rooms (in this case the “bubbles”) with the ‘infinite’, or at least immeasurable Earth-face, and the different rooms with each-other. Observations and applications of this method for long years, led to the following simplified, drawn-manifesto (Figure 1).

Figure 1: Spaceprints.

- Architecture deals with two essential domains: space and nonspace.

- Space contains non-space [3].

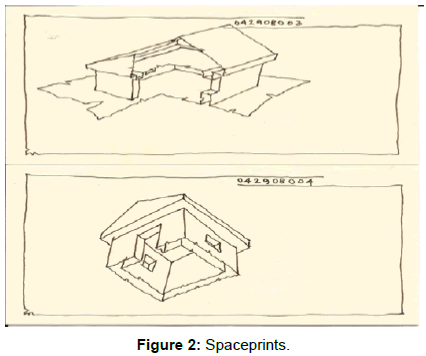
-The interface of these domains is named "Spaceprint", it simultaneously describes the localized shapes of both space and nonspace. - The condition of spatial continuity is surface continuity (Figure 2).

Figure 2: Spaceprints.

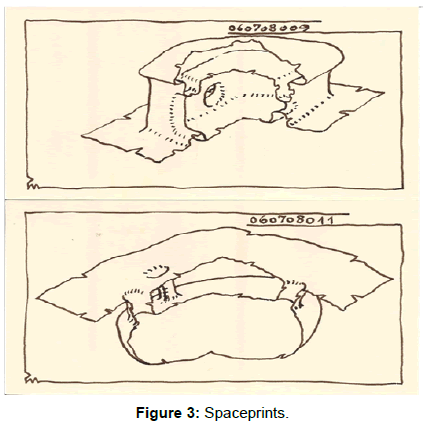
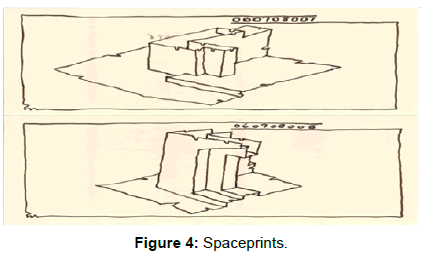
- Common behavior in the practice of architecture, that we are talking about space, yet non-space is drawn (Figures 3 and 4).

Figure 3: Spaceprints.

Figure 4: Spaceprints.

- "Particular Spaceprints" could describe the shapes of an object and as well as of space.

-Intentionally or unintentionally, these spaceprints are imagined in architectural design, and materialized in building construction.

- In construction, one distinguishes surface providers and surface holders.

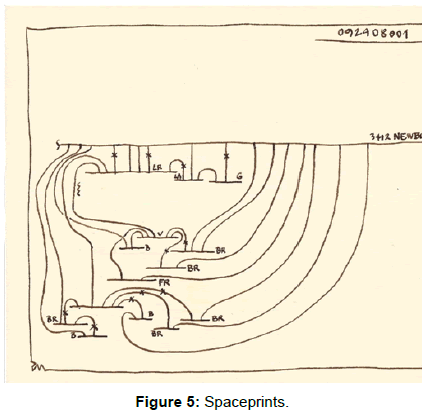
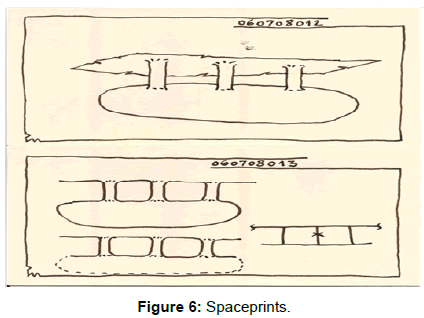
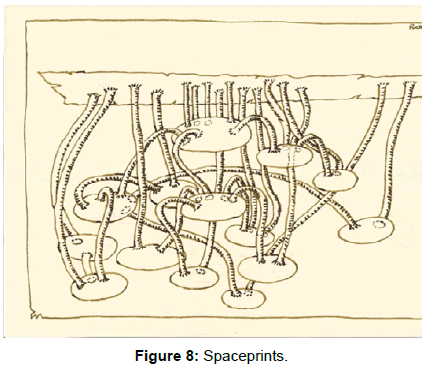
-Traditional materials are bifunctional, while new structures show distinct separation of these two functions (Figures 5-8).

Figure 5: Spaceprints.

Figure 6: Spaceprints.

Figure 7: Spaceprints.

Figure 8: Spaceprints.

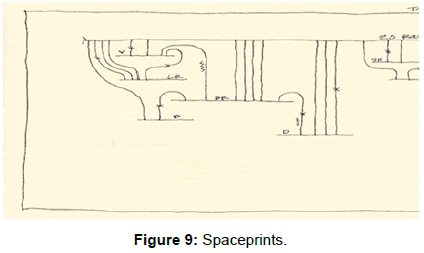
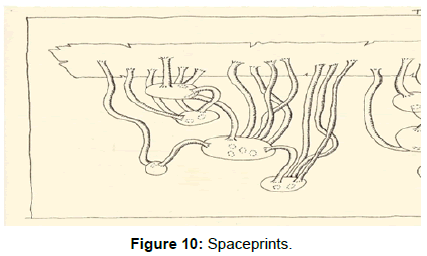
-"Spaceprint Fragments" describe surface strategies; changes in the surface usually denote changes in the structures and/or materials (Figures 9 and 10).

Figure 9: Spaceprints.

Figure 10: Spaceprints.

- Applying to the "Particular Spaceprints" the rules of topology, where metric properties (measurements, directions, proportions) are not preserved, only the neighborhood relationships, we can create the "General Spaceprints".

- Every "Particular Spaceprint" can be transformed to only one "General Spaceprint", but this latter could be reversed to numberless versions of the former.

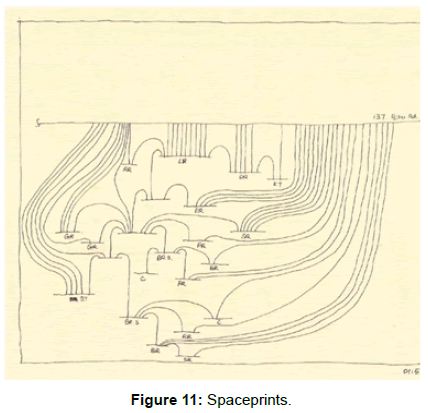
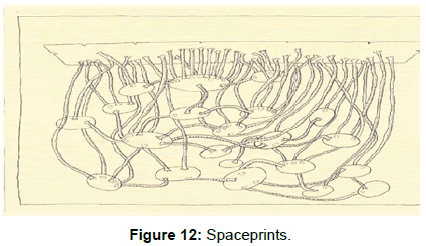
- Topological transformations are often called 'rubber-sheet- geometry', hence the rounded shapes and tube-like openings. These latter representing the doors, windows and other openings, seamlessly connect internal surfaces with the external ones (Figures 11 and 12).

Figure 11: Spaceprints.

Figure 12: Spaceprints.

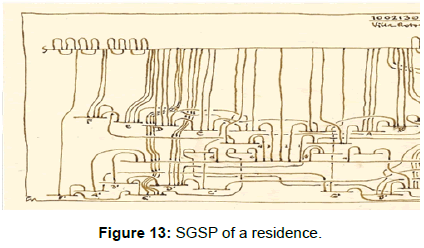
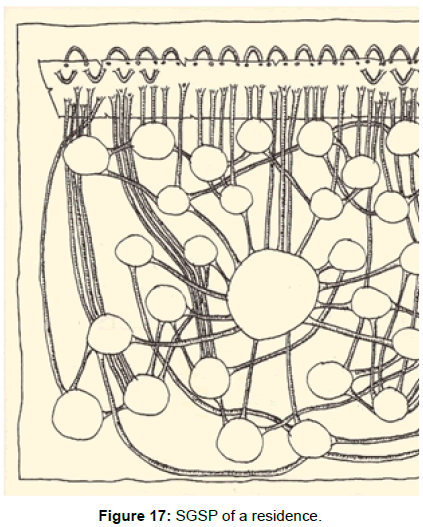
-Applying the infinite pliability of these imaginary surfaces, the "General Spaceprints" can be transformed and the result is the "Simplified General Spaceprint" or SGSP (Figure 13).

Figure 13: SGSP of a residence.

(If I may indulge in the patience of my readers, let me recommend them to visit the following You Tube video: http://www.youtube.com/ watch?v=JhxyTozjHE).

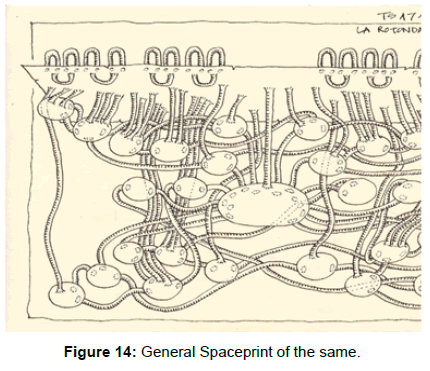
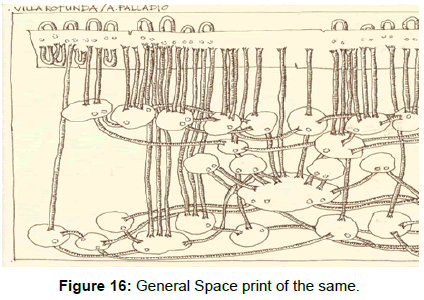
This reduction method resulted a relatively simple tool, which denotes spatial structure, and as such, could be applied in analytical and comparative studies of space in architecture. As a shorthand depiction, they could be used as a programming tool, (in a SGSP format) or in the ‘bubbles and tubes’ version, they can reveal spatial relationships of any building. These characteristics enable this process, to be applied for the establishment of spatial typologies (Figures 14-16).

Figure 14: General Spaceprint of the same.

Figure 15: SGSP of a residence.

Figure 16: General Space print of the same.

The following drawings are but the first batch of a collection of Simplified General

Spaceprints and General Spaceprints

They are the intermediary elements, through which my investigation method relates to the subject of this particular issue of OZ: complexity.

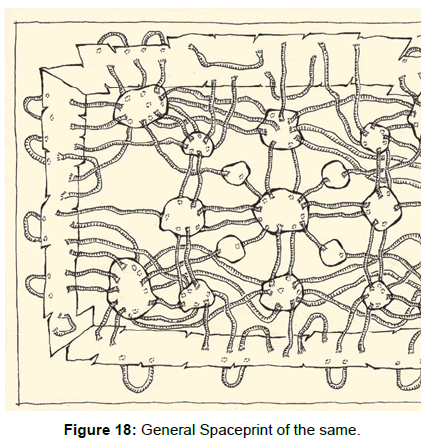
The visual boundaries – internal or external – allow us to perceive only partial relationships of spatial connectivity! They graciously reduce complexity to visually easily digestible sights. Simplicity is still a governing principle, when the shaping of individual spaces, or even the external appearance of a building is concerned (Figures 16-18).

Figure 17: SGSP of a residence.

Figure 18: General Spaceprint of the same.

However, under this seemingly simple space-perceptions, the incredible complex spatial structure is hidden, and so far, the Spaceprint method might be the only one, which is able to reveal the complex system of spatial loops, which are present even in a seemingly simple building. The following drawings are excerpts from the works of some of the students in my “Spaceprint Seminar”, when they had to map out their respective residencies, in both of the Simplified General Spaceprint, or in the General Spaceprint forms. As a final test of their analytical abilities, based on my SGSP drawing, they had to visualize and draw the General Spaceprint of Antonio Palladio’s well-known Villa La Rotonda. This centrally symmetrical building was chosen due to its seemingly simple and repetitious spatial system, only to be surprised by the inherent complexity of the spatial structure. If at the earlier shown examples one didn’t recognize the obvious visual symbolism between these General Spaceprints, now it is inevitable to not to see them as root-systems, the Roots of Infinity=√∞ (Figures 18 and 19).

Figure 19: SGSP of Palladio’s Rotonda.

This interpretation of Architecture reveals omnipresent, but newly formulated aspects for the enrichment and ritualization of our spatial perception. With the application of the theoretical tools of reduction and topological transformation, the infinite expansion of space, at least cognitively, can be comprehended. Myriad attempts were made to discover a believable and shared symbolism [4].

Architecture since the lost secrets of the renaissance

The obvious but lost symbol is its cosmic scale! The perception of the presence of gravity and spatial infinity is also very rarely happens. One can easily imagine, that in the case of even one, or many, high-rise buildings, how complex, and literally, deep-rooted this connection, and symbolic representation of anchoring infinity could become. We can talk about low-, medium -, high-, super- and hyper-intensity degrees, and the number of mangrove-like “roots” in the cities (= “root -fields”) Once understood, that even the simplest building has an intimate, and mostly hidden relationship to infinity, architects suddenly became the new priests and shamans of our society, because they do, what their awed predecessors were doing: speak to and with Cosmos!.

Acknowledgement

The author would like to express his appreciation to Wesley Gross and Elias Logan, the editors of OZ 36, for their constructive comments and assistance! Also I am indebted to the students, credited at the list of figures, for their permission to use the drawings, and for those also, whose work didn’t get into the journal, but worked diligently and with great curiosity towards the topic. Professor Ray Streeter’s photo of the Villa La Rotonda lent a beautiful aura to this issue of OZ!

References

1. Valery P (1960) Eupalinosoul’Architecte. Gallimard, Paris, France.
2. Piaget J (1956) The Child’s perception of Space. North Western University Press, Chicago.
3. Edie JM (1964)The  Primacy  of  Perception.NorthWestern University Press, Chicago.
4. Magyar P (1999) Thought Palaces.Architectura&NaturaPress, Amsterdam NL.