The Role of a BCC Alloy for Hydrogen Storage
Received: 07-Apr-2017 / Accepted Date: 28-Apr-2018 / Published Date: 05-May-2018
Abstract
Hydrogen storage alloys for electrochemical application have been extensively studied for many years. We have presented a review of recent research activities on metal hydride alloys for nickel metal hydride battery and also provided an overview of the use of metal hydrides in other electrochemical applications. AB5 and AB2 alloys are very well established systems. In order to potentially dominate the future electric vehicle and stationary applications, self-discharge, low-temperature performance, and cycle stability become more important to study, and the trend of recent research reflects the efforts on improving the aforementioned properties. The most abundant element in the universe, have greatest potential as substitution energy source with following advantages. Renewable energy source and Non-polluting and forms a bi product as water.
Keywords: Metal hydride; Hydrogen storage alloy; Fossil fuels cell
Introduction
Hydrogen storage alloys are important for a few electrochemical applications, especially in the energy storage area. The basic of electrochemical use of the hydrogen storage alloy can be described as follows: when hydrogen enters the lattice of most transition metals, interstitial metal hydride (MH) is formed. At present 70% of the world energy demand is met by the fossil fuels, because of their availability and convenience for use [1-4]. Until 2000 coal and nuclear fuel partially replace the petroleum products. If leading steps are taken to reduce the cost for these processes, the use of solar energy will increase. To use solar energy as a major source it is highly desirable to store it in a concentrated form that can be easily transported. Main topics of research in this field are hydrogen production, storage and transmission, vehicles and hydrogen combustion, chemical and metallurgical usage, overall system, environmental and material aspects and industrial aspects. Heat storage and heat pumping generations of hydrogen by electrolysis and thermolysis of water. Tritium generation, separation and storage in nuclear fission and fusion reactor [5-7].
In this dissertation, the theoretically estimated diffusion parameters of hydrogen isotopes, hydrogen and deuterium in the BCC metal α-Fe have been presented. A lattice dynamical approach using green function techniques and scattering matrix formation is adapted to work out the displacements of hydrogen isotopes and host crystal atoms. Using these displacement values, reaction coordinates are calculated [8-11].
Materials and Methods
In the lattice dynamical approach of the estimation of diffusion parameters, the first step is to calculate the phonon frequency spectrum of the host metal lattice, since these values in addition to their corresponding Eigen vectors are involved in the calculation of the displacements of defect space atoms [12,13]. This chapter explains the theoretical model used for the study of lattice dynamics of α-Fe. The theoretical model based on Basic theory of lattice dynamics and Construction of the dynamical matrix, Wave vectors Calculations, Lattice Green’s Function and, Diffusion Parameters [14,15].
As the unit cell of the monatomic bcc lattice consists of single atom, the dynamical Matrix ‘D’ is of order 3 × 3. The various elements of this
Matrix are shown below:
D (1, 1)=[F+2A1 cos2πqx+2B1 (cos 2πqy+cos 2πqz)]/Mass
D (2, 2)=[F+2A1 cos 2πqy+2B1 (cos 2πqx+cos 2πqz)]/Mass
D (3, 3)=[F+2A1 cos 2πqz+2B1 (cos 2πqx+cos 2πqz)]/Mass
D (1, 2)=D (2, 1)=((4/3) (A–B) [cos πqz sin πqx sin πqy]/Mass
D (1, 3)=D (3, 1)=(4/3) (A–B) [cos πqy sin πqz sin πqx]/Mass
D (2, 3)=D (3, 2)=(4/3) (A–B) [cosπqx sinπqy sin πqz]/Mass
Where Force constant is:
F=(8/3) (A+2B)-(2/3) (A+2B) [cosπ (qx+qy+qz)+cosπ (qx+qy+qz) +cosπ (qx-qy+qz)+cosπ (-qx+qy+qz)]
The force constant parameters A and B represent the first neighbour interactions; A1 and B1 represent the second neighbour interaction qx, qy and qz are the x, y and z components of the wave vector and ‘Mass' is the mass of the metal atom. Diagonalization of this dynamical matrix yields the Eigen values and their corresponding Eigen vectors. To get the full frequency spectrum, the matrix diagonalization is carried out for the 73 representative wave vector points of the bcc lattice. These wave vector points with the associated statistical weights (SW) are tabulated in Table 1.
| Parameters | For a-Fe |
|---|---|
| A | 7.51807 |
| B | -0.3968 |
| A1 | 0.76704 |
| B1 | -0.13793 |
Table 1: Force constant parameters in units of 104 dynes/cm.
These parameters are arranged in Table 2 with these parameters a very good fit to the experimental dispersion relations have been obtained.
| Parameters | H in a-Fe | 2H in a-Fe |
|---|---|---|
| A1 | 5.0497 | 4.97132 |
| B1 | 8.0696 | 7.92966 |
| C1 | -3.01126 | -2.95834 |
| A | -0.18086 | 1.11095 |
| B | -12.41611 | -12.32251 |
| A3 | -8.06521 | -8.06521 |
| B3 | 0.64645 | 0.64645 |
Table 2: The force constant parameters involved in the calculation of the matrix elements.
Diffusion parameters
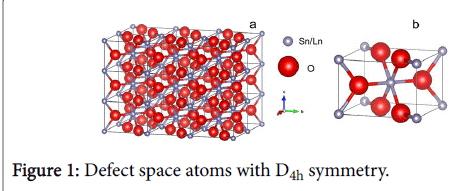
When interstitial atom is in the 0 position, there are two nearest neighbour metal atoms at (001) r0 and r0 and four next nearest neighbours at r0, where r0 is half the lattice constant. Thus the defect space consists of seven atoms as shown in Figure 1.
The displacements of six metal atoms in the defect space are calculated using the equation:
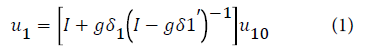
The interstitial Green’s function matrix γ is of order 3 × 3 which is defined as:
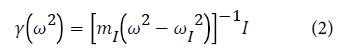
The displacement of the interstitial hydrogen atom is calculated using the equation:
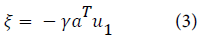
The elements of the δ1 matrix consist only of the change in force constant values and are calculated using Morse potential. The matrix consists of force constant parameters representing metal-hydrogen interaction:
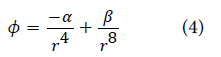
The force constant parameters involved in the calculation of the matrix elements δl and a are shown in Table 2.
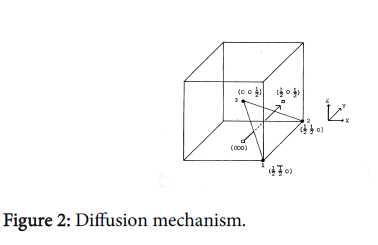
When hydrogen tries to jump from 0-0, as shown in Figure 2 there are atoms in a plane at r0,(110) r0 and (001) r0 to obstruct the jumping atom. The reaction coordinates for this jump are calculated using the equation:
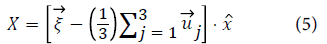
Results and Discussion
Mean square displacements of defect space atoms
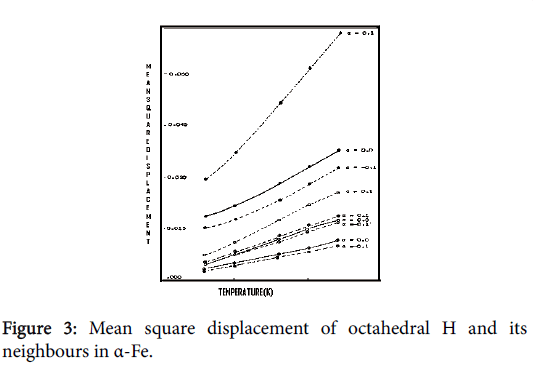
At low concentration, there is a random distribution of H/2H in the interstitial positions of the bcc metal lattice, without disturbing the original lattice structure. Thus there are seven atoms in the defect space. This sub-section reports our calculated MSD values of defect space atoms in the presence of H and 2H in α-Fe. The algorithm employed for the calculation has been discussed in chapter 2. Since H prefers octahedral position in α-Fe, calculation has been carried out for this position only. The Temperature range of our calculation is 300-1200 K. MSD values of defect space atoms for H/2H interstitials in α-Fe are shown in Figures 3 and 4. The continuous line is for α=0.0, the upper dotted line is for α=0.1 and the lower dotted line is for α=-0.1. For these systems of our study, neither experimental or theoretical results are available at present except the x-ray diffraction measurement on the host crystal values of 0.08, 0.090 and 0.095 Å2 respectively for the temperatures 800, 1000 and 1200 K. From Figures 3 and 4, it is clear that our results of MSD of the defect space metal atoms are smaller than the above experimental values. It has been observed that the changes in MSD values with relaxation for defect space metal atoms are small. But for H/2H, there is much change in MSD values with relaxation. This may be due to the low mass of H/2H comparing to that of metal atoms.
Diffusion parameters
A comparison of these results with that of H in α-Fe has been made in Table 3.
| (1/T)*103K-1 | H in a-Fe | 2H in a-Fe | DH/D2H |
|---|---|---|---|
| 1.25 | 3.94 | 2.26 | 1.74 |
| 1 | 5.77 | 3.86 | 1.49 |
| 0.83 | 7.45 | 5.51 | 1.35 |
Table 3: A comparison of these results with that of H in a-Fe.
From Table 3 it is clear that the results of 2H in α-Fe are less than that of H in α-Fe as expected. The rations DH/D2H with temperature are also given in the same Table 3. It is clear that this value of DH/D2H approaches the classical value of √2 at higher temperatures as expected. This indicates that our results are of correct order.
Conclusion
Hydrogen storage alloys for electrochemical application have been extensively studied for many years. We have presented a review of recent research activities on metal hydride alloys for nickel metal hydride battery and also provided an overview of the use of metal hydrides in other electrochemical applications. AB1 and AB2 alloys are very well established systems. In order to potentially dominate the future electric vehicle and stationary applications, self-discharge, lowtemperature performance, and cycle stability become more important to study, and the trend of recent research reflects the efforts on improving the aforementioned properties. Laves phase-related BCC solid solution has high capacity; enhancing its stability is currently the most essential topic. The most abundant element in the universe, have greatest potential as substitution energy source with following advantages. Renewable energy source and non-polluting and forms a bi product as water.
References
- Schmitt R (1976) Process for manufacturing a negative accumulator electrode for the reversible storage and restitution of hydrogen. US Patent 3: 726A.
- Willems JG (1984) Metal hydride electrodes stability of LaNi5-related compounds. Philips J Res 39: 1-94.
- Anani A, Visintin A, Petrov K, Srinivasan S, Reilly JJ, et al. (1994) Alloys for hydrogen storage in nickel/hydrogen and nickel/metal hydride batteries. J Power Sources 47: 261-275.
- Kleperis J, Wójcik G, Czerwinski A, Skowronski J, Kopczyk M, et al. (2001) Electrochemical behavior of metal hydride. J Solid State Electrochem 5: 229-249.
- Feng F, Geng M, Northwood DO (2001) Electrochemical behaviour of intermetallic-based metal hydrides used in Ni/metal hydride (MH) batteries: A review. Int J Hydrog Energy 26: 725-734.
- Hong K (2001) The development of hydrogen storage electrode alloys for nickel hydride batteries. J Power Sources 96: 85-89.
- Wessells C, Ruffo R, Huggins RA, Cui Y (2010) Investigations of the electrochemical stability of aqueous electrolytes for lithium battery applications. Electrochem Solid-State Lett 13: A59-A61.
- Nakayama H, Nobuhara K, Kon M, Matsunaga T (2010) Electrochemical properties of metal hydrides as anode for rechargeable lithium ion batteries. Electrochem Soc 6: 4574-4608.
- Dong H, Kiros Y, Noréus D (2010) An air-metal hydride battery using MmNi3.6Mn0.4Al0.3Co0.7 in the anode and a perovskite in the cathode. Int J Hydrog Energy 35: 4336-4341.
- Mizutani M, Morimitsu M (2010) Development of a metal hydride/air secondary battery with multiple electrodes. Electrochem Soc 28: 545-549.
- Osada N, Morimitsu, M (2010) Cycling performance of metal hydride-air rechargeable battery. Electrochem Soc 218: 194.
- Weng G, Li CV, Chan K (2013) High efficiency vanadium-metal hydride hybrid flow battery: Importance in ion transport and membrane selectivity. Electrochem Soc 223: 242.
- Weng G, Li CV, Chan K (2013) Study of the electrochemical behaviour of high voltage vanadium-metal hydride hybrid flow battery. Electrochem Soc 223: 484.
- Weng G, Li CV, Chan K (2012) Exploring the role of ionic interfaces of the high voltage lead acid-metal hydride hybrid battery. Electrochem Soc 372: 372.
- Purushothama BK, Wainright JS (2012) Analysis of pressure variations in a low-pressure nickel-hydrogen battery. J Power Sources 206: 421-428.
Citation: Pari C, Mohan N (2018) The Role of a BCC Alloy for Hydrogen Storage. J Mater Sci Nanomater 2: 106.
Copyright: © 2018 Pari C, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Share This Article
Recommended Journals
Open Access Journals
Article Usage
- Total views: 3607
- [From(publication date): 0-2018 - Apr 01, 2025]
- Breakdown by view type
- HTML page views: 2839
- PDF downloads: 768