The Importance of Uncertainty in the Noise Pollution Measurements

Department of Industrial Engineering (DIIn), University of Salerno, via Giovanni Paolo II, 132, Fisciano (SA), Italy

*Corresponding Author:

Alessandro Ruggiero
Department of Industrial Engineering (DIIn)
University of Salerno, via Giovanni Paolo II
132, Fisciano (SA), Italy
E-mail: ruggiero@unisa.it

Received date: October 17, 2016; Accepted date: October 25, 2016; Published date: November 01, 2016

Citation: Ruggiero A (2016) The Importance of Uncertainty in the Noise Pollution Measurements. Environ Pollut Climate Change 1:102.

Copyright: © 2016 Ruggiero A. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Visit for more related articles at Environment Pollution and Climate Change

Abstract

The commentary aims to discuss the importance of uncertainties determination in the measurement of noise pollution focusing the attention on the variability of the measure and as a source of uncertainty and offers an overview of the actual research results trends.

Keywords

Noise control; Noise pollution measurements; Measurement uncertainty.

Introduction

Currently in all part of the world there is a considerable interest in the problem of noise pollution reduction for the high numbers of people affected by this phenomenon. A number of studies demonstrate that high levels of sound pressure can damage people’s health in a variety of ways, making initiatives to control noise a study of key importance to society [1-3].

Generally the limits of acceptable environmental noise levels are based on the Equivalent Continuous Sound Level (weighed A), L_eq,Α [dBA], that is a measure of sound pressure level (SPL) over a measurement time t₂-t₁:

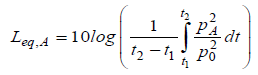
in which p_A is the acquired sound pressure (varying in time) weighed in frequency by using the A-curve, and p_rif is the sound pressure reference value (20 μPa).

In the major parts of the cases these values are measured by level meters following ISO standards (i.e., ISO 1996-1:2016, ISO 1996- 2:2007) or legislative impositions to obtain synthetic quantities to be compared with the imposing limits: it is important to underline that any comparison between a measured value and a threshold level permitted in law (or in technical standard) is a complex subject. This is because it is well known that this is not trivial the comparison between two fixed numerical values, since a measurement is only an estimation (or approximation) of the measurand value. In the comparison, it is essential to take into account the uncertainties associated with the measurement, as reported for international technical standards [4], because uncertainties are a quantitative indication of the reliability of the result, according with ISO IEC Guide 98-4, Uncertainty of measurement–Part 4 [5].

In recent years there has been remarkable interest amongst the researchers in the field of acoustics about the quantification of environmental noise measurement uncertainties [6-8]. In particular, there has been deep examination of possible sources of uncertainties principally due to the characteristics of measurement instrumentation, the variability of the measurement conditions, and the instrumentation calibration [9].

An example of application of the Guide to the Expression of Uncertainly in Measurement (GUM), which involves instrumentation technical specifications of the technical standards on electro-acoustics, is the uncertainty estimation of a class 1 sound level meter. With reference to a generic stationary outdoor noise source, it was estimated [10] that the value that takes into account the inherent uncertainties contributions, weather conditions (temperature, humidity, pressure), linearity, frequency corrections (A-curve), microphone isotropy, but which does not take into account the positioning of the measuring instrument, is about 0.49 dB. The global uncertainty u, assuming that its components are uncorrelated, can be calculated as:

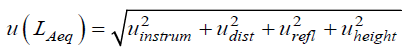
where:

u_instrum is the uncertainty associated to the measurement instrumentation [dB];

u_dist is the standard uncertainty associated to the distance between source and receiver [dB];

urefl is the standard uncertainty associated to the distance of microphone from reflective walls [dB];

uheight is the standard uncertainty associated to the height of the microphone above the ground [dB];

However, to provide an satisfactory estimation of the total uncertainty associated with the measurement of the equivalent level of environmental noise, the intrinsic variability of the measurand cannot be ignored [11].

Actual Research Trends

In the last years the interest of the scientific community toward the determination of uncertainty due to the intrinsic variability of the measurand was increased. Some authors, such as Paviotti and Kephalopoulos in [12], performed investigations on the noise measurement uncertainty, focusing on road traffic acquired data and estimating long-term environmental noise indicators. The main assumption of the analysis is the Gaussian distribution for the measured data. Further, others authors such as, WszoÅ?ek and KÅ?aczyÅ?ski [6] explored the subject examining real statistical distributions of traffic noise SPL registered in several reference points, verifying that the distributions of the (short period) acoustic levels were not strictly related to any known statistical distribution. Then, considering that it is very difficult to postulate any probability distribution of the long-term environmental noise indicators, Batko and Stepien in [13] proposed the application of bootstrap methods, having they a wide applicability in many cases, while in [14] a non-classical model of interval estimation based on the kernel density estimator was proposed.

Considering that the environmental noise is composed of many independent acoustical signals generated from different acoustic sources and that often they are affected by special events that are not characteristic of the acoustic environment under observation [11], new techniques were proposed in [1]. They are based on the “outlier” detection rules for obtaining a “purified” representative noise signal and then on the consecutive application of computer code, developed by using algorithms based on bootstrap methods [7]. This allows to treats acoustical dataset with no restrictions in terms of time behaviour and sound pressure levels statistical properties. With the resampling procedures, the distributions can be considered as approximations of the true distributions of the measurand and thus a good approximation of the distribution of relevant statistics, such as the mean value and the standard deviation. This method, at the moment, was proved to be successfully applicable to the case of traffic noise measurement [7,15] that represents one of the most relevant noise source in the life environment and will be in the next future tested on different dataset representative of different acoustic climates.

Conclusion

At present, acoustic measurement uncertainty determination is very important in noise pollution assessments especially in order to quantify the probability of the success of a decision when a comparison between a measured level and a legislative (or technical) limit value is needed.

Focusing the attention of the uncertainty due to the measurand variability, in the last years many researches were conducted, allowing to conclude that the right direction could be toward the analysis of several measured dataset regarding different noise sources by using bootstrap methods joined with outlier detections rules.

The author believe that this approach can have widespread application and, thanks to the streamlined structure can be easily integrated into applied noise measurement instrumentation in order to provide real-time information on the measurand uncertainty value due to its variability.

References

1. Ising H, Kruppa B (2004) Health effects caused by noise: Evidence in the literature from the past 25 years. Noise Health 6: 5-13.
2. Passchier-Vermeer W, Passchier WF (2000) Noise exposure and public health. Environ health perspect 108: 123-131.
3.  Ruggiero A, Quartieri J, Guarnaccia C, Hloch S (2015) Noise pollution analysis of wind turbines in rural areas. IJER 9: 1277-1286.
4. Ruggiero A, Quartieri J, Guarnaccia C, Hloch S (2015) Noise pollution analysis of wind turbines in rural areas. IJER 9: 1277-1286.
5. ISO IEC Guide 98-4, Uncertainty of measurement âÂ?Â? Part 4: Role of measurement uncertainty in conformity assessment ASME B89.7.3.1-2001, Guidelines to Decision Rules in Determining Conformance to Specifications.
6. JCGM 100 (2008) Evaluation of measurement data âÂ?Â? Guide to the expression of uncertainty in measurement.
7. Wszolek T, Klaczynski M (2006) E?ect of tra?c noise statistical distribution on LAeq, T measurement uncertainty. Archives of Acoustics 31: 311âÂ?Â?318.
8. Liguori C, Paolillo A, Ruggiero A, Russo D (2016) LâÂ?Â?incertezza nelle misure di rumore ambientale. Tutto misure 1: 21-24.
9. UNI Progetto U20.00.135.1:2008, Acustica âÂ?Â? Valutazione dellâÂ?Â?incertezza nelle misurazioni e nei calcoli di acustica âÂ?Â? Parte 1: Concetti generali.
10. Garai M (2008) Espressione dellâÂ?Â?incertezza in acustica applicata: stato dellâÂ?Â?arte e prospettive. Convegno Nazionale AIA, Milano, p: 35.
11. Ruggiero A, Russo D, Sommella P (2016) Determining environmental noise measurement uncertainty in the context of the Italian legislative framework. Measurement 93: 74-79.
12. Liguori C, Paolillo A, Ruggiero A, Russo D (2015) Towards the evaluation of the measurement uncertainty of environmental acoustic noise. Proceedings of 2015 IEEE International Instrumentation and measurement Technology Conference.
13. Paviotti M, Kephalopoulos S (2008) Expected mean in an environmental noise measurement and its related uncertainty. J Acoust Soc Am 123: 3148.
14. Batko W, Stepien B (2010) Application of the bootstrap estimator for uncertainty analysis of the long-term noise indicators. Acta Physica Polonica A 118: 11-16.
15. Stepien B (2016) Confidence intervals for the long-term noise indicators using the kernel density estimator. Archives of Acoustics 41: 517-525.