Small-Signal Stability Analysis with Wind Power Penetration in the INPS Network
Received: 05-Aug-2020 / Accepted Date: 16-Sep-2020 / Published Date: 28-Sep-2020
Abstract
The electric power system continuously faces the problem of low frequency oscillatory stability due to lightly loaded synchronous generators connected to weak grid, variable loads and overloaded tie lines. This paper examines the problem of power system oscillation in the Integrated Nepal Power System (INPS). Furthermore, the potential effect of integration of wind turbine generation is also studied. The points for wind power injection are chosen suitably. The eigenvalue analysis is then run to identify the critical modes of oscillation as well as the participation factor which helps to identify the potential problematic area in INPS with respect to small-signal stability. Moreover, the transient stability is analyzed with the help of time domain analysis. Our study results depict that the integration of doubly fed induction generator (DFIG) has both beneficial and detrimental effects in INPS. All the simulation results are analyzed and validated using the Power System Analysis Toolbox (PSAT).
Keywords: Small-signal stability; Synchronous generator; Wind power penetration; Integrated Nepal power system (INPS)
Introduction
Growing environmental concerns and efforts to reduce dependency on traditional fossil fuels are promoting the development of alternative energy resources worldwide. In the context of Nepal, distributed generation is also getting huge attention as a alternative for conventional form of generation. Among the various renewable resources, wind power has the most promising technical and economic prospects [1]. However, with the proliferation of wind power generation, the influence of it on power system dynamics and stability should not be underestimated. In fact, the dynamic behavior of a power system is largely determined by the behavior and interaction of the generators connecting to the power system. A few studies on analysis and control of small signal stability of power system can be found in [1-4]. The implications of wind power on practical power systems around the globe has been studied by many researchers [5-7]. This includes revisiting damping performance of the grid in the presence of wind power.
Connecting the wind farm into power system will affect the stability characteristics of the local grid. Over the years, more and more scholars have begun to pay attention to the stability of power system with high share wind power. It is recognized that the wind turbine itself will not participate in electromechanical oscillations or bring new oscillating modes, but the wind power output can affect the damping of the power system [1-7]. The effect of DFIG-based wind turbine on the power system small signal stability is analyzed in [8-10], which is the most widely used wind turbine type. The study of small signal stability using PSAT is achieved by some researchers in [11,12].
Critical challenge for Nepal and the hydro industry is the continuing reduction of water resources due to climate change. The unpredictable but steadily declining hydrology has revealed a severe vulnerability in the ability of the hydro sector to meet the claims of electrifying the nation and this challenge is becoming increasingly insurmountable. To make an appreciable reduction in the dependency on Hydro power by the use of PV systems and wind energy, a large number of PV generators and wind turbines have to be embedded in the network. However, large scale installation of renewable sources will give rise to potential power system problems as seen in above mentioned papers. This includes voltage stability problem, protective device coordination problems, unintentional islanding, and angle stability problem. However, a control and monitoring system across the network would have to be highly reliable. Power system stability is one of the major aspects that need to be identified especially small signal stability since the oscillations caused by this type of stability have resulted many incidents.
Thus, by taking problems highlighted in the above paragraphs, the main contributions of this paper are:
• Detailed analysis of power system oscillations in the INPS using eigenvalue analysis.
• Study of effect of DFIG wind penetration on low frequency oscillatory stability in the INPS network
Small Signal Stability
Small signal stability is the ability of the power system to maintain synchronism under small disturbances [13]. Such disturbances occur continually on the system because of small variations in loads and generations. There may be two cases of instability: Steady increase in rotor angle due to lack of synchronizing torque or rotor oscillates of increasing amplitude due to lack of sufficient damping torque. The nature of system response to small disturbances depends on a number of factors including the initial operating, the transmission system strength and the type of generation excitation controls used.
In modern power system, insufficient damping of oscillations creates the problem of small-signal stability. The stability of the following types of oscillations is of concern [13,14].
1. Local modes or machine modes are associated with the swinging of units at a generating station with respect to the rest of the power system. The oscillations are localized at one station or a small part of the power system in local mode. The frequency ranges of these modes is from 0.8 Hz to 2.5 Hz.
2. If many machines in one part of the system are swinging against machines in other part, then that is inter area mode. These are caused by two or more groups of closely coupled machines being interconnected by weak ties. The frequency of these modes’ ranges from 0.1 Hz to 0.8 Hz.
3. Control modes are associated with the generating units and other controls. Poorly tuned exciter, speed governors, HVDC converters and static VAR compensators are the usual cause of instability of these modes.
4. Modes associated with the turbine-generator shaft system rotational components is Torsional modes. Interactions of the shaft oscillations with excitation controls, speed governors, HVDC controls and series-capacitor-compensated lines result in the instability of torsional modes.
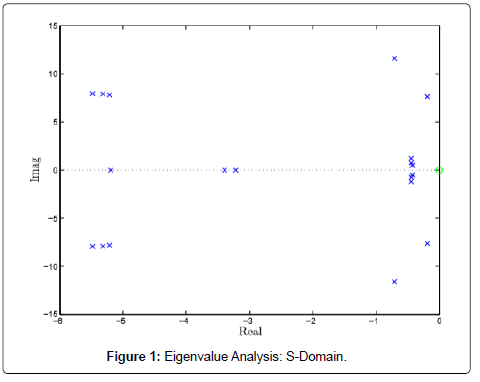
The automatic voltage regulator action enhances a positive synchronizing torque for a high value of external system reactance and high generator output, but may produce a negative damping torque component. Such effect is more pronounced as the exciter response increases. Although a high response exciter is beneficial in increasing synchronizing torque but in doing so, it introduces a negative damping. Thus, there is conflicting requirement with regard to exciter response. So, a compromise is to be made and this can be achieved by setting the exciter response so that it results in sufficient synchronizing and damping torque component for the desired range of system operating conditions. This may not be always possible. Sometimes high synchronizing torque may be required for the transient stability performance which can be achieved by high response exciter. With a very high external system reactance even with low exciter response, the net damping torque coefficient may be negative Figure 1.
Eigenvalue and Stability
The time dependent characteristics of a mode corresponding to an Eigenvalue λ_i is given by e^(λ_i t). So the stability of the system is determined by the eigenvalues as:
a) A real Eigenvalue corresponds to a non-oscillatory mode. A negative real eigenvalue represents a decaying mode. The larger its magnitude, the faster the decay. A positive real eigenvalue represents aperiodic instability.
b) Complex eigenvalues occur in conjugate pairs, and each pair corresponds to an oscillatory mode.
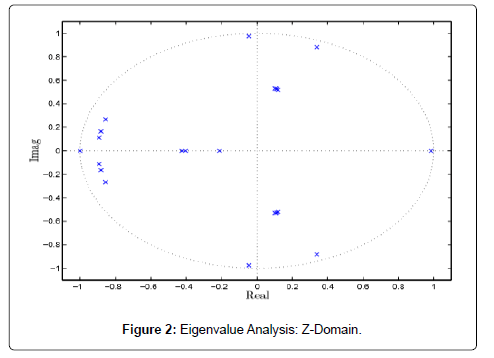
Using PSAT, eigenvalues can be computed either in S-domain and Z-domain. In S-domain, the system is stable if the real part of eigenvalues is less than zero, while in Z-domain, if all the eigenvalues are inside the unit circle, then the system is assumed stable, which makes ease the visualization of very stiff system Figure 2.
During this Study, Eigenvalues are computed in S-Domain.
Simulation Model
INPS is taken to study small-signal stability with wind power generation. Total generations and load at the west of Butwal is connected as one generator and load at Butwal. Similarly, Eastern Region generations and loads are connected at Lahan. Some underconstruction generating projects which are completing soon like Tamakoshi, Upper Sanjen, Upper Trisuli etc. are included within the network. Transmission voltages and load voltages of 132 KV and 66 KV are only considered. Scenario without Wind Integration is assumed as a base case. Pi (π) model of transmission line is considered. Tamakoshi Hydropower (456 MW) is taken as a slack bus. Small Generating stations less than 2 MW are ignored in load flow. All the generators are considered to supply full load capacity during peak load time. Dynamic and economic analysis of Power flow is not considered. Wind turbine generator used is variable speed Doubly Fed Induction Generator.
In Nepal, six wind buffer zone is identified [15]. Among those points, wind power is penetrated at three point of common coupling (PCC) during this analysis. Those points are Pokhara (for Kagbeni and Thini), Hetauda (for Phakhel nad Voleni Makawanpur) and Panchkhal (for Ramechhap and Sindhuli).
To make the study more practical, relatively small amount of wind power is integrated in the system. Among the total load estimated 1400 MW load in INPS system, around 2%, 4% and 6% i.e. 10 MW,20 MW and 30 MW of wind power is penetrated at each point. Most critical Eigenvalues, their participation factor, generator rotor angle oscillation after interruption and Wind power variation at different operating scenario are presented below.
Results and Discussions
Base case
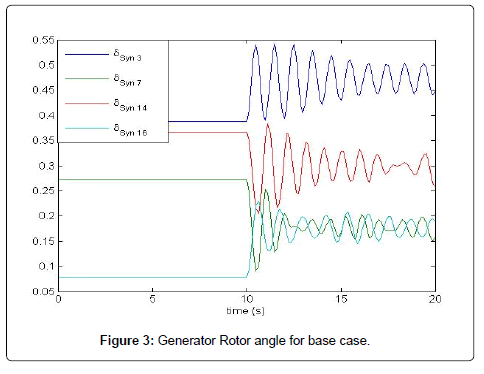
As the network consists of large number of generators and loads connected through weak transmission lines, there are numbers of critical eigenvalues. It can be seen from the result that all the eigenvalues has negative real parts which signifies that the system is primarily smallsignal stable. Among those eigenvalues, the most three critical values, their most associated states, frequency and damping factors are shown in Table 1. The mode type can be identified by analysis the participation factor (Figure 3).
| Real part | Imaginary part | Frequency(Hz) | Damping Factor | Most Associated states | Mode Type |
|---|---|---|---|---|---|
| -0.00027 | ± 7.85 | 1.24 | 0.0034% | Δδ1, Δω1 | Inter-area |
| -0.00792 | ± 7.618 | 1.21 | 0.10% | Δδ5, Δω5 | Local |
| -0.00417 | ± 7.72 | 1.228 | 0.054% | Δδ8, Δω8 | Local |
Table 1: Critical Eigenvalues of INPS Base case.
From Table 2, it is seen that the most critical Eigenvalue is associated with Δδ1, Δω1 (i.e. generator of Sanjen) and Δδ16, Δω16 (generator of Modikhola). Generators in central region can be assumed as one area and generators from western region can be another area Table 3. In most of the cases, single generator or generators within a single oscillates against the rest of the network. There are only few cases when generators from different area oscillates against each other Table 4. After installing PSS at Modikhola and Sanjen, then the eigenvalue with most associated states of (Δδ1, Δω1) and (Δδ16, Δω16) becomes -0.248 ± 7.055 i.e. damping becomes 3.5%from 0.00044% and -0.19284 ± 7.63 i.e. damping 2.53% (Figure 4).
| Critical Eigen Values | Δδ1, Δω1 | Δδ5, Δω5 | Δδ7, Δω7 | Δδ8, Δω8 | Δδ9, Δω9 | Δδ16, Δω16 | Mode |
|---|---|---|---|---|---|---|---|
| -0.00027 ± 7.85 | 26.40% | - | - | - | - | 22.75% | Inter-area |
| -0.00792 ± 7.618 | - | 21.47% | - | 3.8% | 21.04% | - | Local |
| -0.00417 ±7.72 | - | - | 3.2% | 28.5% | 16.44% | 7.7% | Local |
Table 2: Participation factor of INPS-Base case.
| Real part | Imaginary part | Frequency (Hz) | Damping Factor | Most Associated states | Mode Type |
|---|---|---|---|---|---|
| -0.00017 | ±7.851 | 1.24 | 0.0022% | Δδ16, Δω16 | Inter-area |
| -0.00276 | ±7.684 | 1.22 | 0.035% | Δδ8, Δω8 | Local |
| -0.00401 | ±7.589 | 1.2 | 0.052% | Δδ9, Δω9 | Local |
Table 3: Critical eigenvalues for case I.
| Critical Eigen Values | Δδ1, Δω1 | Δδ5, Δω5 | Δδ8, Δω8 | Δδ9, Δω9 | Δδ16, Δω16 | Mode |
|---|---|---|---|---|---|---|
| -0.00017 ± 7.851 | 21.36% | - | - | - | 27.76% | Inter-area |
| -0.00276 ± 7.684 | - | - | 43.4% | 4.1% | - | Local |
| -0.00401 ±7.589 | - | 7.3% | - | 39.37% | - | Local |
Table 4: Participation factor of eigenvalues for case I.
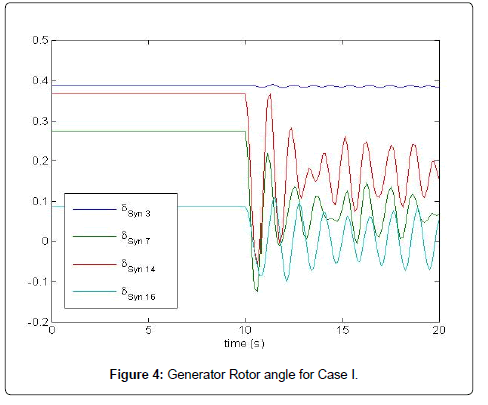
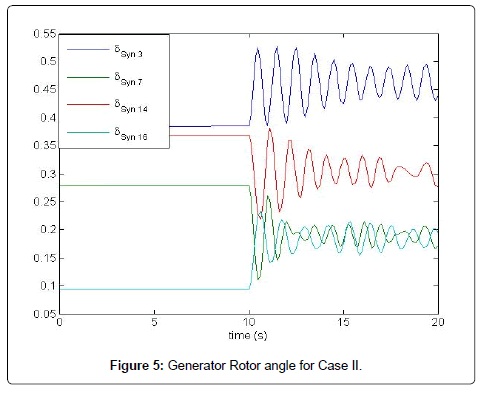
For the Time Domain Analysis, one of the most congested line Marshyandi to Suichatar is disconnected at 10 s. The generator rotor angle and voltage oscillations at different buses decay to steady state confirming the result obtained from the eigenvalue analysis Table 5. In the graph, rotor angle of Trisuli, Indrawati, Kulekhani II and Marshyandi are taken as reference from different area respectively (Figure 5).
| Real part | Imaginary part | Frequency (Hz) | Damping Factor | Most Associated states | Mode Type |
|---|---|---|---|---|---|
| -0.00004 | ± 7.85 | 1.24 | 0.00051% | Δδ16, Δω16 | Inter-area |
| -0.00272 | ± 7.63 | 1.21 | 0.035% | Δδ8, Δω8 | Local |
| -0.00402 | ± 7.536 | 1.19 | 0.053% | Δδ9, Δω9 | Local |
Table 5: Critical eigenvalues of case II.
Damping performance with wind penetration
Case-I Wind Penetration around 2%
Case-II Wind Penetration around 4%
Case-III Wind Penetration around 6%
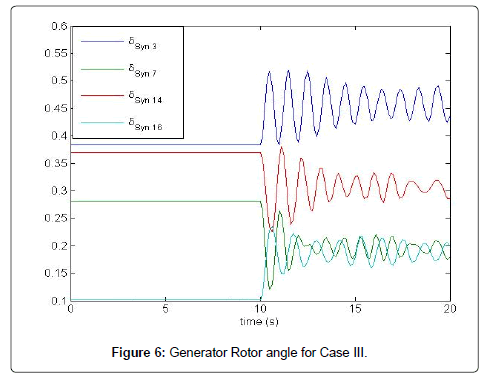
The results presented above provide some crucial insights into the impact of wind turbine generation in the INPS. The most associated state for the most critical electromechanical mode in base case is the differential angle and speed of G1. As the DFIG is connected to the network, then the differential angle and speed of G16 becomes more sensitive for critical eigenvalue. On the other hand, the mode (i.e. -0.1236 ± 7.15518) having Δδ1 and Δω1 as most associated state with 2% wind penetration has 1.72% damping (that was 0.0034% in base case) Table 6. So, it can be said that when DFIG power is injected in one system, it can alter the line flows in stressed line so that angular difference is also altered. As the damping factor is highly dependent on angular difference, the damping factor may increase or decrease (Figure 6).
| Critical Eigen Values | Δδ1, Δω1 | Δδ5, Δω5 | Δδ8, Δω8 | Δδ9, Δω9 | Δδ16, Δω16 | Mode |
|---|---|---|---|---|---|---|
| -0.00004 ± 7.85 | 23.01% | - | - | - | 26.78% | Inter-area |
| -0.00272 ± 7.63 | - | - | 44.84% | 2.88% | - | Local |
| -0.00402 ± 7.536 | - | 11.34% | - | 37.06% | - | Local |
Table 6: Participation factor of critical eigenvalues for case II.
Similar conclusion can be drawn from other eigenvalues also. Thus, it can be inferred from the results that the DFIG penetration can have both detrimental and beneficial effects on large power system from low frequency oscillation perspective. As the wind power penetration increases, due to isolation effect of converter, their control system and different connections of generators and grid, the damping of most critical eigenvalue of large network may reduce Table 7.
| Real part | Imaginary part | Frequency (Hz) | Damping Factor | Most Associated states | Mode Type |
|---|---|---|---|---|---|
| -0.00003 | ± 7.85 | 1.24 | 0.00038% | Δδ16, Δω16 | Inter-area |
| -0.00287 | ± 7.587 | 1.2 | 0.037% | Δδ8, Δω8 | Local |
| -0.00432 | ± 7.4852 | 1.19 | 0.057% | Δδ9, Δω9 | Local |
Table 7: Critical eigenvalues of case III.
From the analysis of possibility of low frequency oscillation in INPS network, one important conclusion can be drawn. It gives the idea of most sensitive generators to the small signal instability. The analysis shows that the state parameters of Chilime, Sunkoshi, Marshyandi, Devighat etc. are more associated with the critical eigenvalues. Upgrading the congested transmission line may be the solution of such problems. Without upgrading the congested transmission line, PSS can be integrated to those generators to increase the stability margin. After installation of PSS in those generators in the networks with 6% wind, the most critical eigenvalue becomes -0.00485 ± 7.485 i.e. damping of 0.065% whereas the damping at same condition without PSS was 0.00038% Table 8.
| Critical Eigen Values | Δδ1, Δω1 | Δδ5, Δω5 | Δδ8, Δω8 | Δδ9, Δω9 | Δδ16, Δω16 | Mode |
|---|---|---|---|---|---|---|
| -0.00004 ± 7.85 | 23.61% | - | - | - | 26.30% | Inter-area |
| -0.00287 ± 7.587 | - | - | 45.6% | 1.2% | - | Local |
| -0.00432 ± 7.4852 | - | 19.83% | - | 29.87% | - | Local |
Table 8: Participation factor of critical eigenvalues for case III.
Conclusion
This study identifies the most critical areas which are prone to small-signal instability both with and without integration of wind generation in the INPS. Our study shows that most of the generators within Bhotekoshi region or within Trisuli-Rasuwa region or Kaligandaki-Pokhara regions shows the local oscillatory behavior and some generators in Sanjen and Modi khola or Trisuli and Gandak shows the interarea oscillatory behavior. Furthermore, our results also depict that the most critical generators with respect to dynamic stability are Sanjen, Sunkoshi, Modikhol, Devighat, Bhotekoshi etc. The damping ratio of eigenvalue associated with generators in Sanjen and Modikhola is a mere 0.0034%. However, the installation of PSS at those critical generators have found to greatly enhances the system damping. Lastly, the integration of DFIG WTGs in the INPS has found to have both beneficial and detrimental effect on the system small-signal stability.
References
- Sun Y, Wang L, Li G, Lin J (2010) A review on analysis and control of small signal stability of power systems with large scale integration of wind power. International Conference on Power System Technology 1-6.
- Wang ZW, Shen C, Liu F (2016) Probabilistic Analysis of Small Signal Stability for Power Systems with High Penetration of Wind Generation. IEEE Transactions on Sustainable Energy 7: 1182-1193.
- Shim JW, Verbic G, Hur K, Hill DJ (2014) Impact analysis of variable generation on small signal stability. 2014 Australasian Universities Power Engineering Conference (AUPEC), 1-6.
- Iswadi H, Morrow DJ, Best RJ (2014) Small Signal Stability Performance of Power System during High Penetration of Wind Generation. 49th International Universities Power Engineering Conference (UPEC), 1-6.
- Modi N, Saha TK, Anderson T (2013) Damping performance of the large scale Queensland transmission network with significant wind penetration. Applied Energy 111: 225-233.
- Byrne RH, Concepcion RJ, Neely J, Wilches-Bernal F, Elliott RT, et al. (2016) Small signal stability of the western North American power grid with high penetrations of renewable generation. 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC) 1784-1789.
- Vowles DJ, Samarasinghe C, Gibbard MJ, Ancell G (2008) Effect of wind generation on small-signal stability-A New Zealand Example. 2008 IEEE Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the 21st Century, 1-8.
- Jia Y, Li Y, Li W (2018) Study on effect of DFIG on small signal stability of power system with high share wind power. 2017 China International Electrical and Energy Conference (CIEEC) 787-791.
- Gautam D, Vittal V, Harbour T (2009) Impact of Increased Penetration of DFIG-Based Wind Turbine Generators on Transient and Small Signal Stability of Power Systems. IEEE Transfer Power System 24: 1426-1434.
- Mehta B, Bhatt P, Pandya V (2014) Small signal stability analysis of power systems with DFIG based wind power penetration. Science Direct Transaction on Electrical Power and Energy Systems 58: 64-74.
- Liu B, Guo H, Gu G (2015) Research on small-signal stability of power system connected with different wind turbines based on PSAT. 2014 17th International Conference on Electrical Machines and Systems (ICEMS) 2: 1330-1333.
- Gurung S, Naetiladdanon S, Sangswang A (2013) Study of Small Signal Stability using PSAT. IJEE Transaction in 2013.
- Kundur P (1994) Power System Stability And Control. McGraw-Hill Inc., New York, USA.
- Kundur P, Paserba J, Ajjarapu V, Andersson G, Bose A, et al. (2004) Definition and Classification of Power System Stability. IEEE Transactions on Power Systems 1401.
- Alternative Energy Promotion Centre (AEPC) (2008) Solar and Wind Energy Resource Assessment in Nepal (SWERA). AEPC, Lalitpur.
Citation: Pandey RP, Gurung S (2020) Small-Signal Stability Analysis with Wind Power Penetration in the INPS Network . Innov Ener Res 9: 238
Copyright: © 2020 Pandey RP, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Usage
- Total views: 2748
- [From(publication date): 0-2020 - Nov 06, 2025]
- Breakdown by view type
- HTML page views: 1924
- PDF downloads: 824