Research Article Open Access
Removal of Lead from Aqueous Solution on Activated Carbon and Modified Activated Carbon Prepared from Dried Water Hyacinth Plant
El-Wakil AM, Abou El-Maaty WM* and Awad FSChemistry Department, Faculty of Science, Mansoura University, Mansoura, Egypt
- *Corresponding Author:
- Dr. Weam Mahmoud Abou El-Maaty
Lecturer of Analytical Chemistry, Faculty of Science
P.O.Box: 35516, Mansoura University, Egypt
Tel: (+2) 01002582722–01099806635
Fax: (050) 2224132–2246254
E-mail: dr.weam_elmaaty@yahoo.com
Received date: February 21, 2014; Accepted date: March 28, 2014; Published date: March 31, 2014
Citation: El-Wakil AM, Abou El-Maaty WM, Awad FS (2014) Removal of Lead from Aqueous Solution on Activated Carbon and Modified Activated Carbon Prepared from Dried Water Hyacinth Plant. J Anal Bioanal Tech 5:187. doi: 10.4172/2155-9872.1000187
Copyright: © 2014 El-Wakil AM, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Analytical & Bioanalytical Techniques
Abstract
In this work, the potential of activated carbon stems and leaves (ACS, ACL) prepared from dried water hyacinth stems and leaves (DS, DL) by chemical activation with phosphoric acid (1:3) and modified activated carbon stems and leaves (MACS, MACL) with nitric acid (1:1) for the removal of lead from aqueous solution was investigated. Carbon samples were produced with a reasonable yield about 75% and have a remarkable surface area (57.46, 71.83, 864.52, 493.78, 381.22, and 265.22 m2/g for DS, DL, ACS, and ACL, MACS and MACL, respectively and well developed pore structure. Batch adsorption experiments were conducted to study the effect of various operating parameters, pH of the solution (1 to 6), initial concentration of lead ions (50 to 400 mg /l), contact time (2-250 min), and temperature (298-323 K). It is obvious that the maximum adsorption of lead at pH 5 is in the order: MACS (175.63 mg/g) > MACL (164.56 mg/g) > DS (90.50 mg/g) > DL (66.60 mg/g) > ACS (36.00 mg/g) > ACL (33.40 mg/g). This may be attributed to the increase in the number of active sites on the modified activated carbon. The equilibrium data were analyzed using Langmuir and Freundlich isotherms. The results showed that the experimental data were fitted well by the Langmuir model. Kinetic results revealed that the adsorption process obeyed a pseudo-second order model and intra-particle diffusion was the rate controlling step. The thermodynamic studies revealed that the adsorption was spontaneous and endothermic process. Desorption of about 90% of the sorbed lead from carbon was achieved using about 0.6 M HCl.
Keywords
Water hyacinth; Activated carbon; Modified activated carbon; Lead; Adsorption
Introduction
The removal of heavy metal contaminants from aqueous solutions is one of the most important environmental concerns because metals are bio refractory, and are toxic to many life forms. Various sources of heavy metals in water are battery manufacturing, basic steel, paper, pulp, metal plating, leather tanning, agrochemicals, petrochemicals, and chemical manufacturing, mining and fertilizer industries. Among the heavy metals, lead is one of the most toxic elements, even at low concentrations. It affects the central nervous system, kidney, liver, and gastrointestinal system, and it may directly or indirectly cause diseases such as anemia, encephalopathy, hepatitis, and the nephritic syndrome [1]. Because of the above factors, there is a necessity to remove these metals from wastewater in order to prevent contamination of natural water bodies by effluents containing toxic metals. The common methods for removing metal ions from water and wastewater include chemical precipitation, oxidation, reduction, reverse osmosis, membrane filtration and adsorption. Among the above methods, the promising process for the removal of metal ions from water and wastewater is adsorption, because the employed adsorbent can be regenerated by suitable desorption process and it is highly effective and economical [2].
Activated carbon is one of the most popular adsorbents for the removal of metal ions from aqueous solutions. Currently, activated carbon is widely used as an adsorbent in wastewater treatments. It has highly developed porosity, a large internal surface area, and relatively high mechanical strength. Despite its widespread use in industries, activated carbon remains an expensive material. Therefore, it is necessary to investigate and develop low-cost effective carbons that can be applied to water pollution control. The properties such as surface charge, type of surface functional groups, specific surface area, and pore-size distribution affect the adsorption capabilities of metal ions on activated carbon. All above mentioned physical and chemical properties of activated carbon depend on the precursor materials and activation methods used [3].
In this article, the possibility of using dried water hyacinth, Carbonized (stems, leaves) and modified Activated Carbon (stems and leaves) as efficient adsorbents for removal of Pb2+ from aqueous solution will be investigated. The effects of pH, initial Pb2+ concentration, and temperature and contact time on adsorption capacities were also examined. Experimental data were analyzed using first order kinetics, pseudo-second order kinetics and intra-particle diffusion model. Also, equilibrium isotherm data were analyzed according to Langmuir and Freundlich equations.
Experimental
Materials and reagents
Stock solution of Lead containing 1 mg lead cm-3 was prepared by dissolving 1.5984 g of Pb(NO3)2 (supplied by BDH) in distilled water and this solution was is completed up to the mark of 1 L measuring flask. Lead solutions of lower concentrations were prepared by further dilution with distilled water. PAR(2-pyridyl azo resorcinol) solution 0.1% (w/v) prepared by dissolving 0.1 g of solid substance in least amount of distilled water then transfers to 100 ml measuring flask and complete to the mark using distilled water. All other chemicals used were of analytical grades.
Preparation of adsorbents
Preparation of dried water hyacinth (DS and DL): The plant water hyacinth was collected from Canal extended from river Nile in Mansoura, Egypt. The roots of the plant were removed while the leaves and stems were washed with water then with distilled water and were soaked in 0.25 M EDTA at pH 10 overnight for removing any metal ions adsorbed on the plant (stems and leaves) and washed with distilled water for several times and dried in oven at 110°C for 48 h then dried stems (DS) and leaves (DL) were ground and stored in desiccators till used in adsorptionexperiments.
Preparation of chemically activated carbon stems (ACS) and leaves (ACL): The dried phase was impregnatedinto 3 times its wt. with concentrated H3PO4 at room temperature for 2 days. then dried in oven at 110°C for 48 h then placed in a muffle oven (in a stainless steel reactor) where the samples were heated gradually in absence of air at a rate of heating=10 K/min up to 550-600°C and then maintained at this temperature for 3 h. After cooling to room temperature, the activated carbon obtained was washed thoroughly with distilled water until the pH of the supernatant become steady at about (pH=6). After that, the samples were dried at 110°C for 24 h. Finally, the Activated carbon prepared from stem (ACS) and leaves (ACL) were ground and stored in desiccators till used in adsorption experiments.
Modification of the activated carbon stems (MACS) and leaves (MACL): The activated carbon (ACS and ACL) were modified by surface oxidation with concentrated nitric acid (1:1 dilution from 67% concentrated HNO3). The modification procedure was as follows. A known volume of 1:1 diluted nitric acid was heated at 110°C. The appropriate amount of ACS or ACL was added to the boiling nitric acid solution at a ratio of 1 g AC to 5 ml nitric acid solution. It was treated for 3 h to increase the formation of functional groups, such as carboxylic acids. The residual material was washed with distilled water until the pH of the supernatantbecome steady at about (pH=6). The modified activated carbon by using nitric acid was then dried at 120°C for 24 h and then were ground and stored in desiccators till used in adsorption experiments.
Batch adsorption experiments
Adsorption isotherms were studied by adding 0.025 g of DS, DL, ACS, ACL, MACS and MACL into 25 ml solutions with initial concentrations of Pb (II) ranging from 5 to 400 mg/L. The initial pH values of the solution were 5. After the suspensions were shaken for 2 h, the remaining concentrations of Pb (II) was analyzed by measuring the absorption of the respective PAR (2-pyridyl azo resorcinol) complex (PAR–Pb) at 520 nm employing a modification of the method proposed by Dagnall et al. [4]. Specifically, 10 ml of buffer solution (borate buffer pH=10) was added to metal solution followed by addition of 1 ml PAR (0.1 g/100 ml), then complete to 25 ml using distilled water. The amounts of Pb2+ removed by sorbents qe and percent extracted %E can be calculated using the following equations:
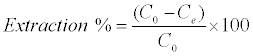 (1)
(1)
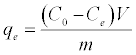 (2)
(2)
Where qe is the amount of Pb2+ adsorbed (mg/g). Co and Ce are the initial and equilibrium liquid-phase concentrations of Pb2+ (mg/g), respectively. V is the volume of the solution (L), and m is the weight of the sorbent used (g).
To study the effects of pH on Pb (II) adsorption, 0.025 g of the adsorbent were dispersed into 25 ml solutions containing 250 mg/L of Pb(II). The initial pH values of the solutions were adjusted from 1.5 to 6 using 0.01 M HNO3 and 0.01 M NaOH.
Kinetic experiments were performed by using different flasks containing around 0.2 g of adsorbent in 200-ml solutions containing 200 mg/L of Pb2+. At desired time intervals, 1 ml of aliquots were taken from the suspension and the concentration of Pb2+ is determined spectrophotometrically as described above.
Result and Discussion
Characterization of prepared samples
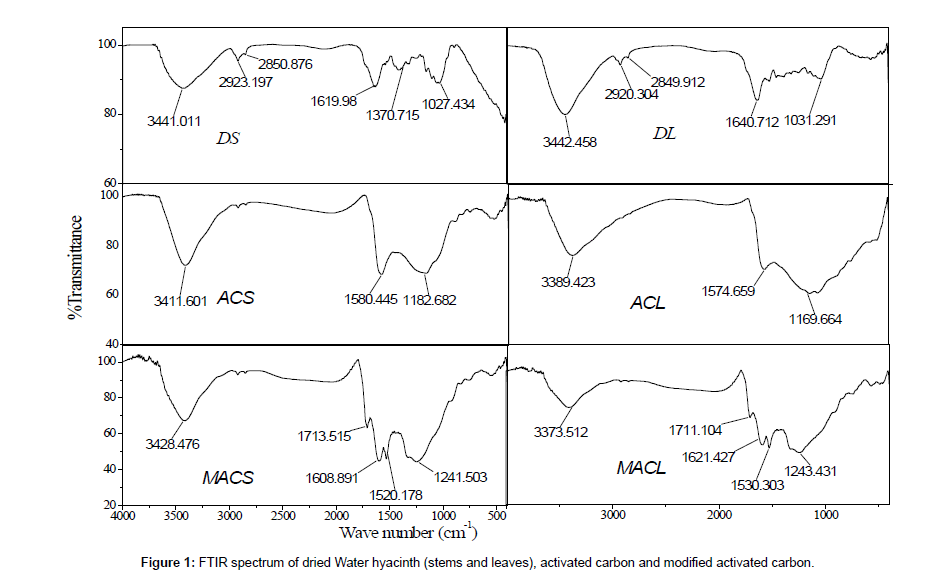
Physic-chemical characterization of MACS, MACL, ACS, ACL, DS and DL were determined as follow: moisture contentdetermined using oven drying method, point of zero charge (pHpzc), surface area was determined from the application of Brunauer Emmett and Teller (BET) equation to the adsorption-desorption isotherm of N2 at 77k [5], as shown in (Table 1). The morphology of MACS, MACL, ACS, ACL, DS and DL examined by electron microscopy is shown in Figure 2. Examination of SEM micrographs obtained clearly indicate the porous structure of different adsorbents at magnification of 1500x, 3500x and 1000x for (DS and DL), (ACS and ACL) and (MACS and MACL), respectively. The FT-IR spectra for similar samples are shown in Figure 1. All samples show wide band at about (3373-3442 cm-1) due to O-H stretching mode of hexagonal group and adsorbed water. The shoulders observed at (2849-2932 cm-1) due to aliphatic (C-H) and appear for all samples [6].The bands near 1600 cm-1 is due to C=C stretching vibration in aromatic ring and is observed for all samples. The bands at (1711-1713 cm-1) for MACL and MACS are due to stretching vibration of carboxyl groups on the edges of layer plane [7]. The weak bands appearing at 1580, 1574, 1240, 1520, 1608, 1243, 1530 and 1621 cm-1 are due to formation of highly conjugated (C=O stretching, C-O stretching in carboxylic groups and carboxylate moieties.) [8].
| Samples | Moisture content % | Surface pH | Surface Area m2/g | Total pore volume | pH PZC |
|---|---|---|---|---|---|
| DS | 6.71 | 5.95 | 57.46 | 0.01 | 4.95 |
| DL | 5.1 | 6.13 | 71.83 | 0.03 | 4.80 |
| ACS | 3.88 | 4.50 | 864.52 | 0.52 | 4.05 |
| ACL | 2.64 | 4.10 | 493.78 | 0.31 | 4.05 |
| MACS | 9.13 | 3.60 | 381.22 | 0.43 | 3.38 |
| MACL | 7.89 | 4.00 | 365.22 | 0.29 | 3.36 |
Table 1: Characteristics of the dried Water hyacinth (stems and leaves), activated carbon and modified activated carbon (stems and leaves).
Adsorption parameters
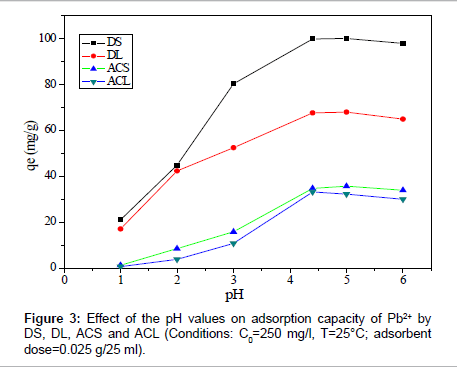
Effect of pH: To optimize the pH for maximum removal efficiency and to avoid the precipitation of Pb (II), a sorption experiment was conducted in the initial pH range from 2 to 6, as shown in Figure 3. The amount adsorbed by DS increased from 21.04 to 102.50 mg/g, for sample DL from 17.10 to 68.04 mg/g, for sample ACS from 1.30 to 35.80 mg/g and for sample ACL from 0.6 to 32.30 mg/g at pH=1 and 5, respectively. At low pH, the surface of the adsorbent was surrounded by hydronium ions that compete with metal ions, which prevented the metal ions from approaching the binding sites on the adsorbent. The increase in metal removal as pH increases can be explained on the basis of a decrease in competition between hydronium ions and metal species for the surface sites. At pH=5.0, the adsorption capacity of (DS, DL, ACS and ACL) almost reaches the maximum value. Because the speciation diagram of lead shows that at pH>6.0 the species such as [Pb(OH)]+, [Pb3(OH)4]+, and [Pb(OH)2] will be produced [9]. In order to guarantee to truly examine the adsorptionproperty of carbon samples as well as to avoid precipitation of Pb(II) ions, all the following experiments were conducted at pH=5.0.
Effect of initial concentration on the uptake of pb2+
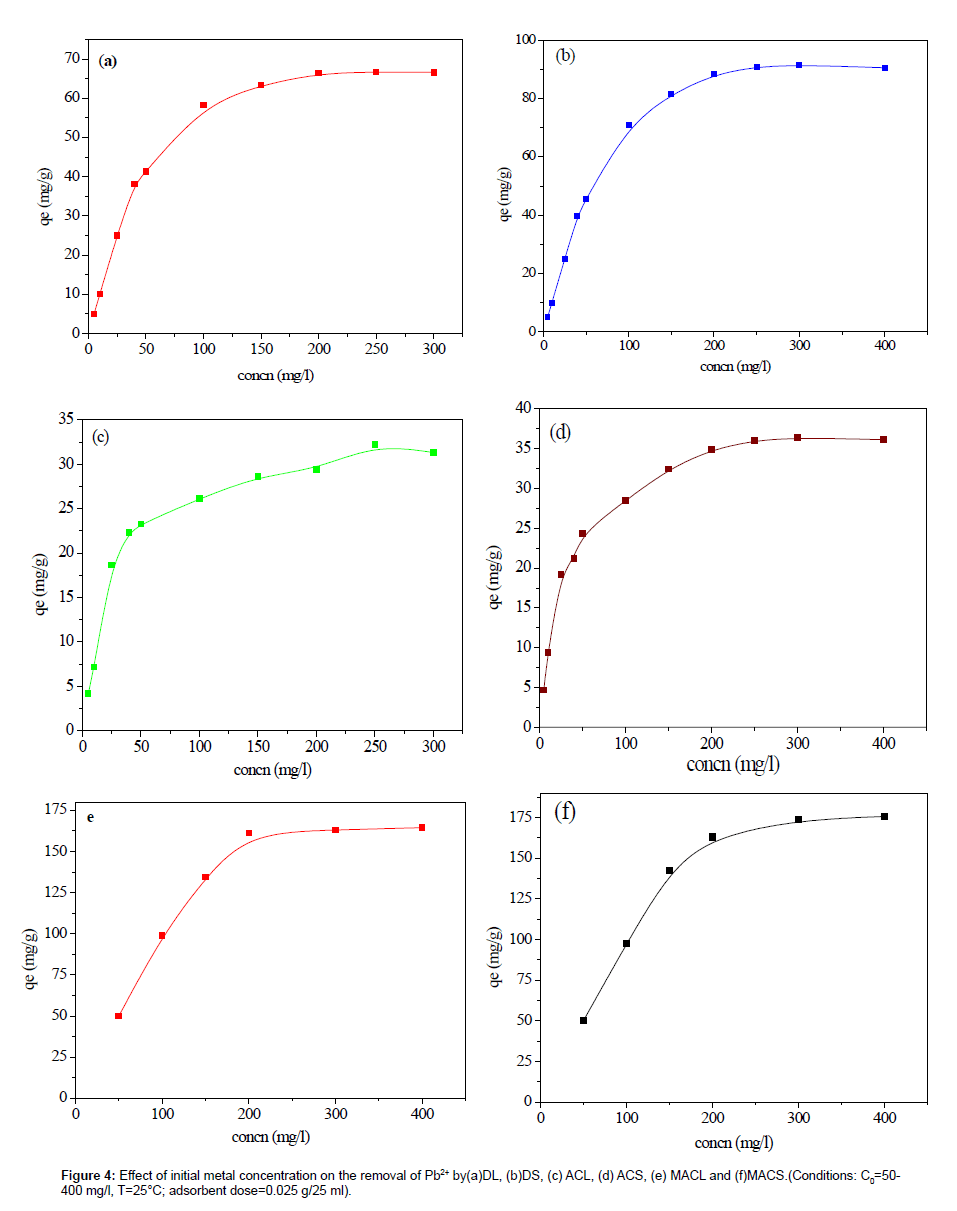
The effect of initial concentration on adsorption was investigated, as illustrated in Figure 4 and 5. It is revealed that, as the initial concentration increased, the adsorption capacities increased. The initial concentration may provide the driving force to overcome the resistance of the mass transfer of Pb(II) between liquid and solid phases [10]. The initial concentration was higher, and then the driving force was higher, and therefore the adsorption capacity would be higher.
Effect of temperature on adsorption
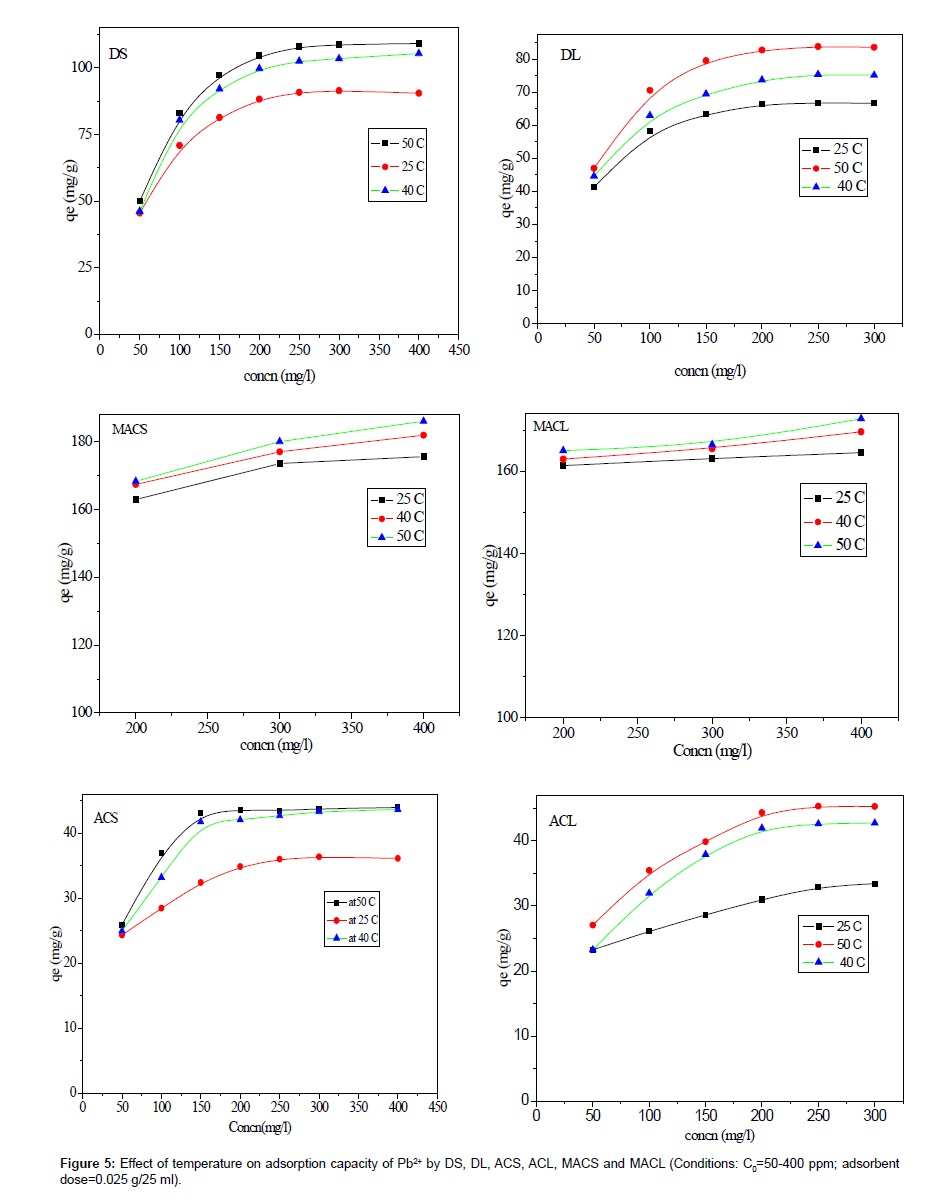
The effect of solution temperature on Pb+2 removal was studied at three different temperatures: 298 K, 313 K and 323 K using DS, DL, ACS, ACL, MACS and MACL. The results are presented in Table 2, and it is obvious from the table that increasing the temperature significantly affected the amount of Pb2+ adsorbed from solution by different adsorbents. The enhancement in the adsorption capacity might be due to the chemical interaction between adsorbate and adsorbent sites or the increased rate of intra particle diffusion of Pb2+ molecules into the pores of the adsorbents as a result of decreasing solution viscosityat higher temperatures and the number of adsorption sites generated because of some internal bonds near the edge of surface active sites of sorbent [11,12].
| Samples | Qe(mg g-1) | ||
| 298 K | 313 K | 323 K | |
| DS | 90.50 | 105.37 | 109.17 |
| DL | 66.60 | 75.14 | 83.54 |
| ACS | 36.00 | 43.00 | 44.00 |
| ACL | 33.40 | 42.72 | 45.25 |
| MACS | 175.63 | 181.96 | 186.07 |
| MACL | 164.56 | 169.62 | 172.79 |
Table 2: Effect of temperature on maximum adsorption capacities of Pb2+ be DS, DL, ACS, ACL, MACS and MACL.
Effect of contact time on adsorption
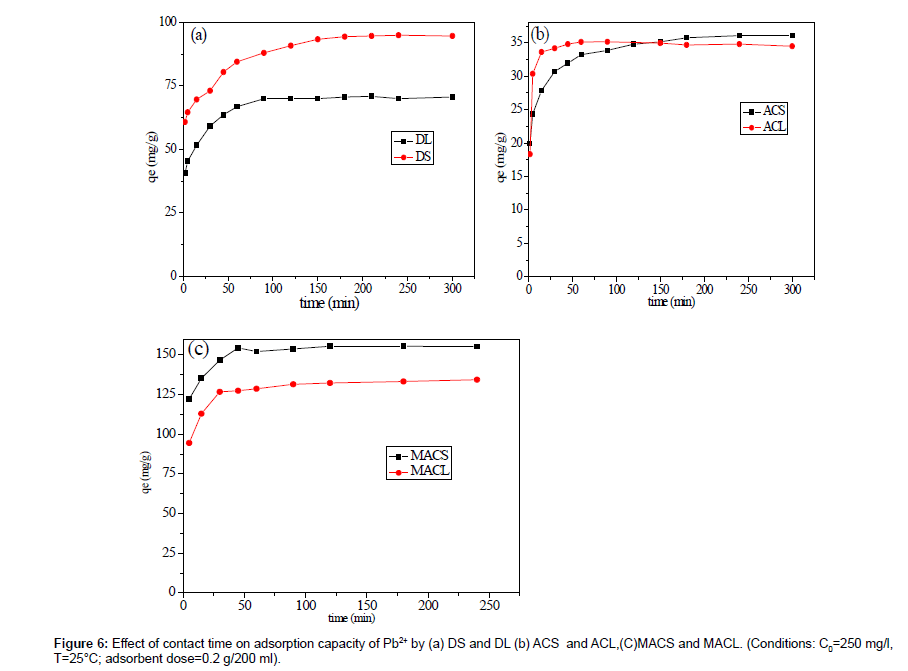
Figure 6 shows the effect of contact time on the percent removal of Pb2+ by (a) DS and DL, (b) ACS and ACL, (C) MACS and MACL at 25°C using a sorbent concentration of 1 g/L at pH 5. The initial concentration of Pb2+ was 200 ppm. It is obvious that, the adsorption amount of Pb(II) rapidly increased at the beginning of adsorption; more than 65% of the adsorption capacities of corresponding adsorbents for Pb2+ occurred within 5 min for DS and DL and more than 88% occurred within 5 min for ACS and ACL and about 90% occurred within 15 min for MACS and MACL. Pb2+ uptake almost remained constant after 60 min for MACS, MACL, ACS and ACL and after 90 min for DS and DL so 90 min could be considered the equilibrium time of the Pb (II) adsorption. The fast adsorptionat the initial stage may be due to the higher driving force making fast transfer of metal ions to the surface of adsorbent particles and the availability of the uncovered surface area and the active sites on the adsorbent.
Effect of adsorbent dosage
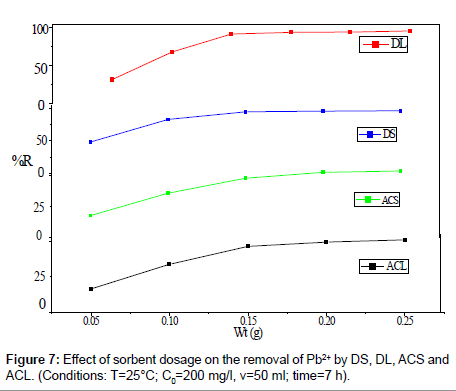
The effect of amount of DS, DL, ACS and ACL on the removal percentage of Pb2+ was shown in Figure 7. It could be clearly seen that, an increase in sorbent dose is in favor of Pb2+ removal. When the sorbent dose increases from 0.05 to 0.25 g, the percent Pb2+ removal by DS, DL, ACS and ACL increase from 48.40% to 96.36 %, from 31.01% to 95.63% , from 17.9 % to 53.95% and from 16.46% to 50.95%, respectively. Increase in adsorption with adsorbent dosage can be attributed to increased adsorbent surface area and availability of more adsorption sites.
Adsorption isotherms
Adsorption is usually described through isotherms, that is, the amount of adsorbate on the adsorbent as a function of its pressure (if gas) or concentration (if liquid) at constant temperature. Adsorptionisotherm is important to describe how adsorbates interact with adsorbents and so it is important in optimizing the use of adsorbents. Two common isotherm equations namely, Langmuir and Freundlich models were tested [13-15].
The Langmuir isotherm assumes a surface with homogeneous binding sites equivalent sorption energies, and no interaction between adsorbed species. Its mathematical form is written as:
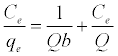 (3)
(3)
Where qe is the amount adsorbed at equilibrium (mg g-1), Ce is the equilibrium concentration of the lead (mg L-1), constant b is related to the energy of adsorption (Lmg-1), Q is the Langmuir monolayer adsorption capacity (mg g-1). The essential characteristics of the Langmuir equation can be expressed in terms of a dimensionless separation factor RL.
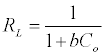 (4)
(4)
C0 is the highest initial solute concentration, b is Langmuir adsorption constant (L/mg), RL indicates the type of isotherm to be reversible (RL=0), Favorable (0<RL>1), Linear (RL=1) or unfavorable (RL>1) [16].
The Freundlich isotherm is an empirical equation based on an exponential distribution of adsorption sites and energies. It is represented as:
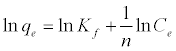 (5)
(5)
Where qe is the amount adsorbed at equilibrium (mg g-1), Ce is the equilibrium concentration of lead (mg L-1), Kf is roughly an indicator of the adsorption capacity, and 1/n is the adsorption intensity. A linear plot of ln qe versus ln Ce confirms the validity of the Freundlich model.
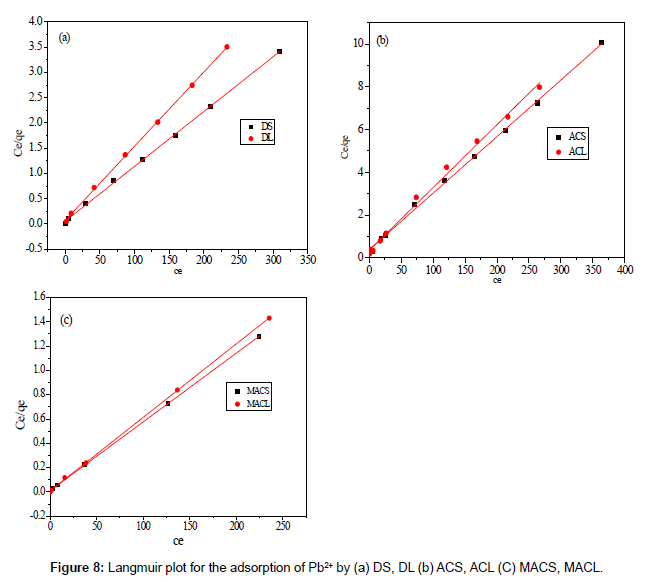
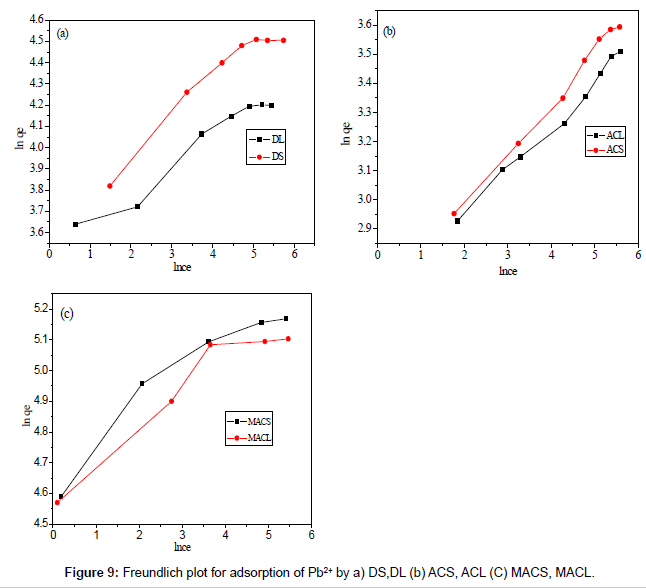
Figures 8 and 9 show the linear plot of Langmuir and Freundlich isotherms for adsorption of Pb2+ on DS, DL, ACS, ACL, MACS and MACL. The model parameters obtained by applying Langmuir and Freundlich models to the experimental data are given in Tables 3 and 4. It can be found that the regression coefficients R2 obtained from Langmuir model are closer to 1 than that of the Freundlich model, suggesting that the Langmuir isotherm fits better with the adsorption of Pb2+ on DS, DL, ACS, ACL, MACS and MACL. In addition, the qmax values for the adsorption of Pb2+ onto the different adsorbents calculated from the Langmuir model are all the same as the experimental data. Also, RL values obtained are in the range of (0.000-0.086), thereby confirming that the adsorption is a favorable process. It can be concluded that the monolayer Langmuir adsorption isotherm is more suitable to explain the adsorption of Pb2+ onto different adsorbents.
| Adsorbents | Langmuir parameters | ||||
|---|---|---|---|---|---|
| R2 | b ( L/mg) | Qmax, fitted | Qexp, | RL | |
| MACS | 0.999 | 0.555 | 176.700 | 175.630 | 0.005 |
| MACL | 0.999 | 0.741 | 165.300 | 164.557 | 0.003 |
| ACS | 0.998 | 0.071 | 37.780 | 36.000 | 0.034 |
| ACL | 0.994 | 0.086 | 33.990 | 33.400 | 0.086 |
| DS | 0.999 | 0.199 | 92.170 | 90.500 | 0.012 |
| DL | 0.999 | 0.221 | 68.070 | 66.600 | 0.016 |
Table 3: Parameters of langmuir isotherm for adsorption of Pb2+ by DS, DL, ACS, ACL, MACS and MACL.
| Adsorbents | Freundlich parameters | ||
|---|---|---|---|
| R2 | Kf | 1/n | |
| MACS | 0.773 | 97.710 | 0.121 |
| MACL | 0.894 | 101.510 | 0.099 |
| ACS | 0.992 | 13.900 | 0.175 |
| ACL | 0.987 | 14.040 | 0.153 |
| DS | 0.926 | 37.880 | 0.168 |
| DL | 0.948 | 33.860 | 0.132 |
Table 4: Parameters of Freundlich isotherm for adsorption of Pb2+ by DS, DL, ACS, ACL, MACS and MACL.
Adsorption kinetics
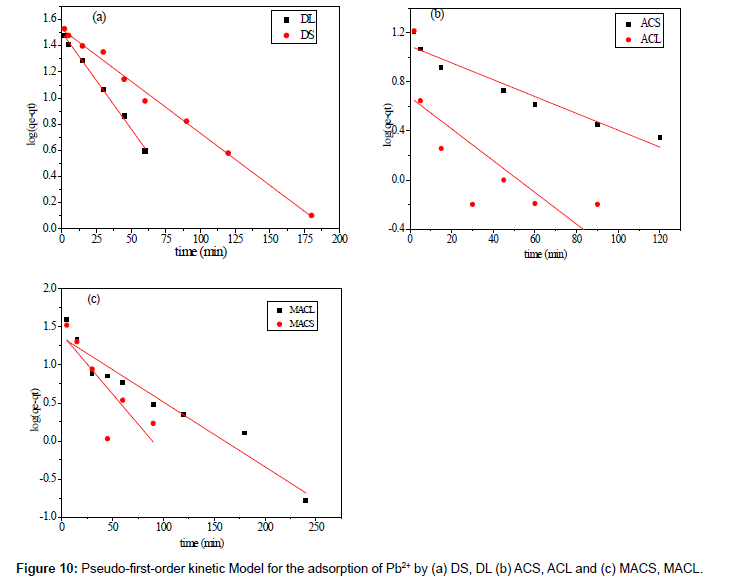
The pseudo-first order equation and the pseudo-second order equation: In order to investigate the controlling mechanism of adsorption process of Pb2+by DS, DL, ACS, ACL, MACS and MACL, the pseudo-first order and the pseudo-second order kinetic models were cited to evaluate the experimental data. The pseudo-first order kinetic model has been widely used to predict metal adsorption kinetics. It was suggested by Lagergren [17] for the adsorption of solid/ liquid systems. The differential form of the pseudo-first order model of adsorption can be expressed as:
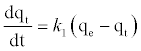 (6)
(6)
Where qe and qt (mg/gm) are the amounts of lead adsorbed at equilibrium and at time t, respectively and k1 is the equilibrium constant (min-1). Integration of equation (6) and by applying the initial conditions qt = 0 at t= 0 and the linear form can be formulated as [18]:
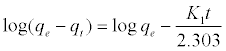 (7)
(7)
Where qe is the adsorption uptake of Pb2+ at time t (mg/g) and k1 (min-1) is the rate constant of the pseudo-first-order adsorption. A plot of log (qe-qt) versus t should be linear; the parameters k1 and R2 (correlation coefficient) calculated from the data (Figure 10) are listed in Table 5. It can be seen that the linear correlation coefficients (R2) for the pseudo-first order kinetic model are high. However, there are large differences between the experimental qe values (qe,exp) and the calculated qe values (qe,cal), which indicated the pseudo-first order kinetic model was poor fit for the adsorption processes of DS, DL, ACS, ACL, MACS and MACL for Pb2+. The differential form of the pseudo-Second order reaction equation may be written as [18,19]:
| Adsorbent Code | qe exp. mg.g−1 | qecal. mg.g−1 | K1 (min−1) | R2 |
|---|---|---|---|---|
| MACS | 155.5 | 4.08 | 0.036 | 0.600 |
| MACL | 134.0 | 3.92 | 0.019 | 0.925 |
| ACS | 35.0 | 2.98 | 0.213 | 0.929 |
| ACL | 33.0 | 1.97 | 0.029 | 0.511 |
| DS | 92.0 | 3.53 | 0.018 | 0.993 |
| DL | 70.6 | 4.49 | 0.034 | 0.997 |
Table 5: Parameters of first order model for adsorption of Pb2+ by DS, DL, ACS, ACL, MACS and MACL.
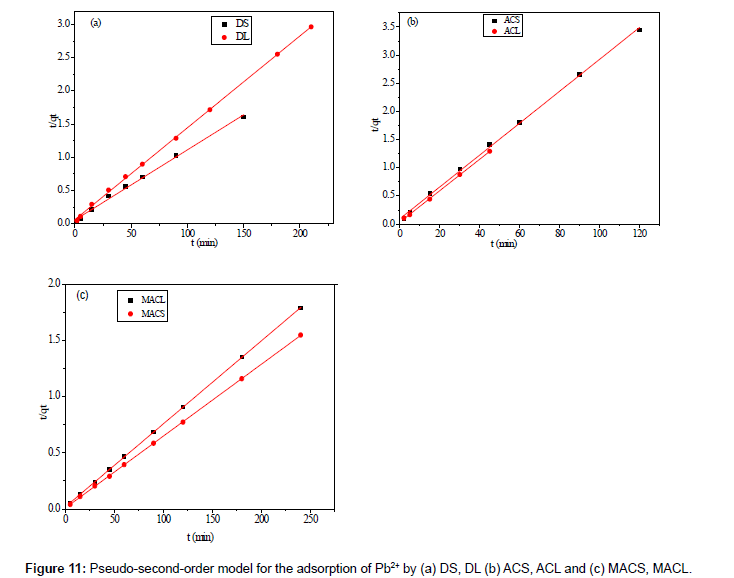
 (8)
(8)
After integration considering the boundary conditions the linearized form of this model can be expressed as [18]
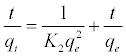 (9)
(9)
Where k2 (g mol-1 min-1) is the rate constant of pseudo-secondorder adsorption. Figure 11 shows the plot of t/q versus t for Pb2+ onto DS, DL, ACS, ACL, MACS and MACL. It can be observed from Table 6 that R2 values for the pseudo-second order kinetic model are all over 0.999, moreover, the qe,cal values for the pseudo-second order kinetic model are all consistent with the qe,exp values. These suggested that the adsorption processes of DS, DL, ACS, ACL, MACS and MACL for Pb2+ can be well described by the pseudo-second order kinetic model. These suggested that the pseudo-second-order adsorption mechanism was predominant referring that adsorption process is controlled by chemisorption which involves valence forces through sharing or exchange of electron between the solvent and the adsorbate Since neither the pseudo-first-order nor the second-order model can identify the diffusionmechanism, the kinetic results were further analyzed by the intra-particle diffusion mode to elucidate the diffusion mechanism.
| Adsorbent Code | qe exp. mg.g−1 | qe cal. mg.g−1 | K2g. mol-1 .min−1. | R2 |
|---|---|---|---|---|
| MACS | 155.5 | 156.49 | 0.041 | 0.999 |
| MACL | 134.0 | 135.50 | 0.027 | 0.999 |
| ACS | 35.0 | 35.34 | 0.009 | 0.998 |
| ACL | 33.0 | 35.84 | 0.002 | 0.999 |
| DS | 92.0 | 94.69 | 0.020 | 0.996 |
| DL | 70.6 | 72.31 | 0.003 | 0.999 |
Table 6: Parameters of second order kinetic model for adsorption of 200 ppm Pb2+ by DS, DL, ACS, ACL, MACS and MACL.
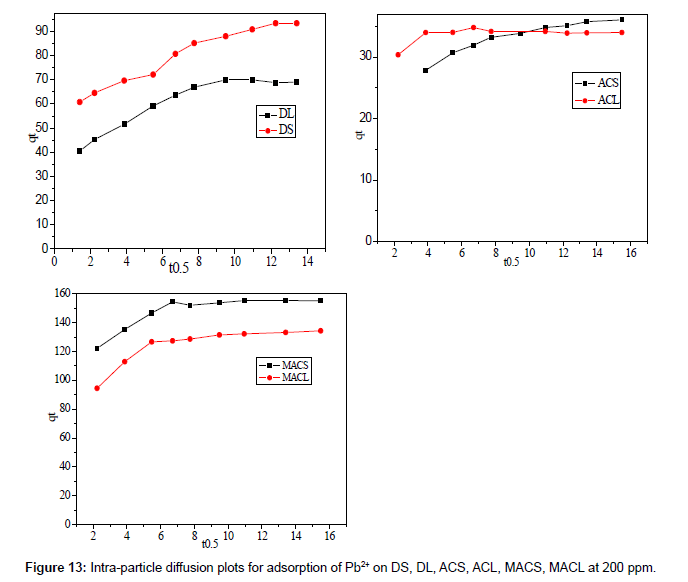
Intra-particle diffusion model: Adsorption is a multi-step process involving transport of solute molecules from the aqueous phase to the surface of the solid particles of adsorbent, and then diffusion of the solute molecules into the interior of the pores, which is likely to be a slow process, and is therefore, rate determining. The intra-particle diffusion parameter, Kd (mg.g-1 h-0.5) is defined by the following equation [20]:
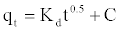 (10)
(10)
Where kd is the intra-particle diffusion rate constant (mg.g-1 h-0.5) and C is a constant. According to this model qt versus t0.5 should be linear if intra-particle diffusion is involved in the adsorption process. From Equation (10), if pore diffusion is the rate limiting step, then a plot of qt against t0.5 must give a straight line with a slope that equals kd and the intercept value C represents the resistance to mass transfer in the external liquid film.
Figure 12 shows the plot of qt against t0.5 for adsorption of 200 ppm Pb2+ by DS, DL, ACS, ACL, MACS and MACL, the plots are multi linear, containing at least three linear segments which indicate that three steps occur during adsorption process. The first sharper portion is transport of Pb2+ from the bulk solution to the adsorbent external surface by diffusionthrough the boundary layer (film diffusion). The second portion is the diffusion of Pb2+ from the external surface into the pores of the adsorbent. The third portion is the final equilibrium stage, where Pb2+ were adsorbed on the active sites on the internal surface of the pores and the intra- particle diffusion starts to slow down due to the solute concentration getting lower and lower in solution In addition, the linear portions of curves did not pass through the origin suggesting that pore diffusion is not the step controlling the overall rate of mass transfer at beginning of adsorption.
In Table 7, the correlation coefficients (R2) for the linear segment intra-particle diffusionmodel were between 0.563 and 0.975, indicating that the intra-particle diffusion was not the only rate-controlling step; other process could control the rate of adsorption. The boundary layer effect may control the rate of mass transfer in the time period of the first linear segment; this conclusion could be corroborated by the analysis of data from Boyd’s model.
| Intraparticle diffusion model | Boyd model | ||||
|---|---|---|---|---|---|
| Adsorbent code | R2 | Kp (mg g-1 min-0.5 ) | Intercept | Intercept | R2 |
| MACS | 0.563 | 2.089 | 130.320 | 0.034 | 0.89 |
| MACL | 0.590 | 2.373 | 104.373 | 1.261 | 0.925 |
| ACS | 0.872 | 0.656 | 27.039 | 0.468 | 0.964 |
| ACL | 0.520 | 0.640 | 30.142 | 0.788 | 0.735 |
| DS | 0.954 | 2.874 | 58.700 | 0.479 | 0.958 |
| DL | 0.975 | 3.764 | 36.848 | 0.167 | 0.982 |
Table 7: Intraparticle diffusion parameters for adsorption of Pb(II) by DS, DL, MACS and MACL at 200 ppm.
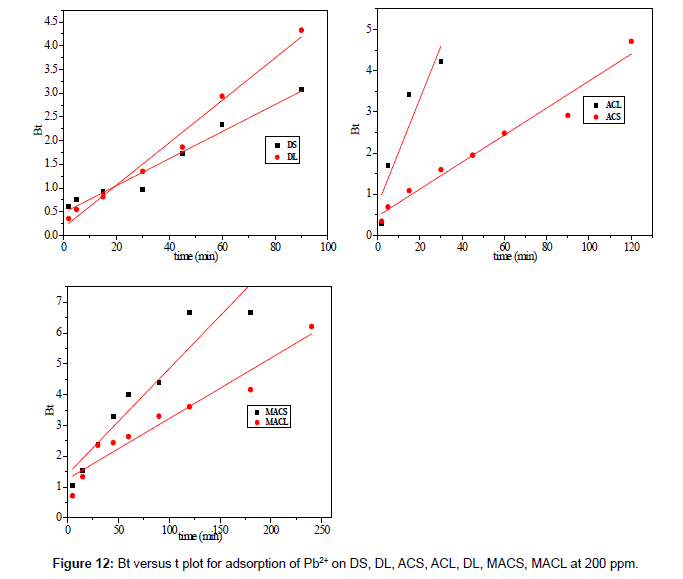
The model of Boyd is expressed as [21]:
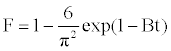 (11)
(11)
Where F is the fractional attainment of equilibrium, at different times, t, and Bt is a function of F.
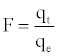 (12)
(12)
Where qt and qe are the metal uptake (mmol g-1) at time t and at equilibrium, respectively.
Equation. (18) can be rearranged to [22]
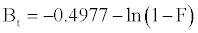 (13)
(13)
Figure 13 shows the values of Bt were calculated from Equation. (13) and plotted against time t. The linearity of this plot can provide available information to distinguish intra-particle diffusion and boundary layer effect (film diffusion) rates of adsorption. If a plot of Bt versus t is a straight line passing through the origin, then adsorption will fit layer effect. The plots are linear only in the initial period of adsorption and do not pass through the origin, indicating that external mass transfer is the rate limiting process in the beginning of adsorption and then is the intra- particle diffusion.
Thermodynamic study
The data obtained from the temperature study were used for thermodynamic analysis. Thermodynamic parameters such as change in standard free energy (ΔG°), enthalpy (ΔH°), and entropy(ΔS°) were determined using the following eqs [23]:
The van’t Hoff equation
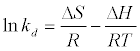 (14)
(14)
ΔG° = ΔH° −TΔS° (15)
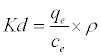 (16)
(16)
Where Kd is the adsorption coefficient, ρ=1000 g/L to make adimensionles Kd [24], ΔG° (J/mol) is the change in Gibbs Free Energy, ΔH°(J/mol) is the enthalpy change of Pb2+ adsorption, ΔS° (J/molK) is the entropy change of Pb2+ adsorption, R is the universal gas constant (8.314 J/mol K) and T is the absolute temperature (K).
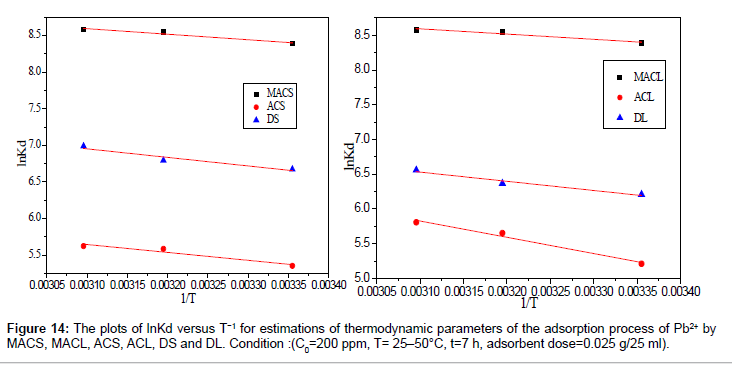
By plotting a graph of ln Kd versus 1/T (Figure 14), the values of ΔH° and ΔS° can be estimated from the slope and intercept of van’t Hoff plots, respectively. The thermodynamic parameters are given in Table 8. It is clear from the table that the values of ΔG° are negative for DS, DL, ACS, ACL, MACS and MACL. The negative values of ΔG° at various temperatures indicate the spontaneous nature of the sorption process. The fact that the values of the ΔG° decrease with increasing temperature indicates the increase of spontaneous effect. For all the sorbents, the positive value of ΔH° suggested the endothermic nature of the adsorption process. Moreover, the positive values of ΔS° point out the increased randomness at the solid/liquid interface during the sorption of Pb2+ by DS, DL, ACS, ACL, MACS and MACL.
| AdsorbentCode | ΔH° (KJ/mol) | ΔS° (KJ/mol K) | ΔG° (KJ/mol) | ||
|---|---|---|---|---|---|
| 298 K | 308 K | 318 K | |||
| MACS | 14.599 | 0.091 | -12.49 | -13.85 | -14.76 |
| MACL | 16.284 | 0.100 | -13.52 | -15.02 | -16.00 |
| ACS | 8.970 | 0.075 | -13.49 | -14.63 | - 15.38 |
| ACL | 11.190 | 0.109 | -21.29 | -22.93 | -24.02 |
| DS | 9.710 | 0.088 | -16.51 | -17.83 | -18.71 |
| DL | 10.990 | 0.088 | -15.35 | -16.67 | -17.56 |
Table 8: Thermodynamic parameters for adsorption of Pb2+ by MACS, MACL, ACS, ACL, DS and DL at different temperatures.
Desorption studies
To achieve practical and economical adsorption, a promising adsorbent is required to have not only high adsorption capacity but also regeneration ability for recycling use. The use of thermal activation to regenerate the adsorbent could require high energy and result in a 5-10% adsorbent loss in each cycle. Hence, Studies were attempted to use chemical regeneration for adsorbate desorption [25]. Desorption of Pb using HCl as a desorping agent by disruption coordination of metal ions and subsequent release from the activated carbon surface into the desorption medium was studied. In order to investigate the desorption capacity of different adsorbents, 0.025 g of different adsorbents were introduced to 25 ml solution of 200 ppm of lead at pH 5. As the adsorption reaches equilibrium, the metal ion concentration of the solution was measured, Then, the adsorbent loaded with lead was collected and treated with 25 ml×M HCl to remove the adsorbed Pb2+. The results relating to desorption of lead by HCl of different concentration are shown in Tables 9 and 10. The results show that increase in concentration of HCl. The desorption also increased but remained constant with 0.6 M HCl.
| Adsorbent code | qe adsorbed | qedesorped | %desorption |
|---|---|---|---|
| MACS | 155.0 | 81.49 | 52.57 |
| MACL | 134.0 | 76.58 | 57.15 |
| ACS | 33.9 | 18.70 | 55.08 |
| ACL | 30.9 | 21.04 | 68.10 |
| DS | 88.2 | 50.00 | 56.70 |
| DL | 64.7 | 49.52 | 76.55 |
Table 9: Desorption efficiencies of Lead using 0.3 M HCl after adsorption of 200 ppm.
| Adsorbent code | qe adsorbed | qedesorped | % desorption |
|---|---|---|---|
| MACS | 155.0 | 126.27 | 81.46 |
| MACL | 134.0 | 117.40 | 87.62 |
| ACS | 33.9 | 30.54 | 90.08 |
| ACL | 30.9 | 28.64 | 92.68 |
| DS | 88.2 | 74.84 | 84.85 |
| DL | 64.7 | 56.17 | 86.82 |
Table 10: Desorption efficiencies of Lead using 0.6 M HCl after adsorption of 200 ppm.
Comparison of the adsorption capacities of sorbents toward Pb2+
Table 11 lists the comparisons of maximum adsorption capacities of Pb2+ on DS, DL, ACS, ACL, MACS and MACL obtained in this study with various adsorbents previously used for the adsorption of Pb2+ [26,27]. The MACS and MACL have a higher adsorption capacity than that of the most other adsorbents reported in the literature, suggesting that it may be potential for Pb2+ removal from aqueous solution.
| Adsorbents | qe (mg/g) | Ref. |
|---|---|---|
| DS DL ACS ACL MACS MACL |
90.50 66.60 36.00 33.40 175.63 164.55 |
This work |
| Siderite Chitosan | 8.58 | [27] |
| Siderite | 12.43 | [26] |
| Rice husk ash | 12.63 | |
| Kaolinite clay | 19.27 | |
| Data pits carbon | 30.66 |
Table 11: Comparison of the adsorption capacities of Pb2+ onto various adsorbents.
Conclusion
Based on the results, it is clear that the Lead-removal values achieved with Nitric acid modified water hyacinth activated carbon were higher than those of dried water hyacinth and activated carbon due to the increase in the number of carboxylic groups on the surface of the modified activated carbon. The main advantages of this removal procedure include (i) simplicity, (ii) cost effectiveness, (iii) rapidity, and (iv) a higher removal efficiency of toxic mercuryions. Based upon the experimental results of this study, the following conclusions can be drawn: It was found that the sorption process is pH-dependent and the maximum adsorption capacity of Pb2+ is at pH 5. It was found that the extent of Pb2+ adsorption increases upon increasing initial concentration and contact time till reached to equilibrium. Pb2+ uptake almost remained constant after 60 min for MACS, MACL, ACS and ACL and after 90 min for DS and DL. The kinetic studies of lead adsorption onto DS, DL, ACS, ACL, MACS and MACL were performed based on pseudo first-order, pseudo second-order, and intra-particle diffusion. The data indicated that the adsorption kinetics of lead on all adsorbents followed the pseudo-second order model at different lead concentrations. The equilibrium data were analyzed using the Langmuir and Freundlich isotherms and the characteristic parameters for each isotherm were determined. The results showed that the experimental data were correlated reasonably well by the Langmuir isotherm model. Thermodynamic studies indicated that the adsorption process was an endothermic process. Desorption of Pb2+ using 0.6 M HCl as a desorping agent by disruption coordination of metal ions and subsequent release from the activated carbon surface into desorption medium was studied.
References
- Momcilovic M, Purenovic M, Bojic A, Zarubica A, Randelovic M (2011) Removal of lead (II) ions from aqueous solutions by adsorption onto pine cone activated carbon. Desalination 276: 53-59.
- Sreejalekshmi KG, Krishnan KA, Anirudhan TS (2009) Adsorption of Pb(II) and Pb(II)-citric acid on sawdust activated carbon: Kinetic and equilibrium isotherm studies. J Hazard Mater 161: 1506-1513.
- Pollard SJT, Fowler GD, Sollars CJ, Perry R (1992) Low-cost adsorbents for waste and wastewater treatment: a review. Science of the total environment 116: 31-52.
- Dagnall R, West T, Young P (1965) Determination of lead with 4-(2-pyridylazo)-resorcinol-I: Spectrophotometry and solvent extraction. Talanta 12: 583-588.
- Ahmed MJ,Theydan SK (2012) Corrigendum to “Equilibrium isotherms and kinetics modeling of methylene blue adsorption on agricultural wastes-based activated carbons”[Fluid Phase Equilib 317 (2012) 9-14]. Fluid Phase Equilibria 318: 115.
- Kennedy LJ, Vijaya JJ, Sekaran G (2005) Electrical conductivity study of porous carbon composite derived from rice husk. Materials chemistry and physics 91: 471-476.
- Guo Y,Rockstraw DA (2006) Physical and chemical properties of carbons synthesized from xylan, cellulose, and Kraft lignin by H3PO4 activation. Carbon 44: 1464-1475.
- Biniak S, Pakula M, Szymanski GS, Swia¸tkowskiA (1999) Effect of activated carbon surface oxygen-and/or nitrogen-containing groups on adsorption of copper (II) ions from aqueous solution. Langmuir15: 6117-6122.
- Machida M, Kikuchi Y, Aikawa M, Tatsumoto H (2004) Kinetics of adsorption and desorption of Pb (II) in aqueous solution on activated carbon by two-site adsorption model. Colloids and Surfaces A: Physicochemical and Engineering Aspects 240: 179-186.
- Aroua MK, Leong SP, Teo LY, Yin CY, Daud WM (2008) Real-time determination of kinetics of adsorption of lead(II) onto palm shell-based activated carbon using ion selective electrode. BioresourTechnol 99: 5786-5792.
- Acharya J, Sahu JN, Mohanty CR, Meikap BC (2009) Removal of lead (II) from wastewater by activated carbon developed fromTamarind wood by zinc chloride activation. Chemical Engineering Journal 149: 249-262.
- Boudrahem F, Aissani-Benissad F,Ait-Amar H (2009) Batch sorption dynamics and equilibrium for the removal of lead ions from aqueous phase using activated carbon developed from coffee residue activated with zinc chloride. Journal of environmental management 90: 3031-3039.
- Dwivedi CP, Sahu JN, Mohanty CR, Mohan BR, Meikap BC (2008) Column performance of granular activated carbon packed bed for Pb(II) removal. J Hazard Mater 156: 596-603.
- Ahmadpour A, Tahmasbi M, Bastami TR, Besharati JA (2009) Rapid removal of cobalt ion from aqueous solutions by almond green hull. J Hazard Mater 166: 925-930.
- Demiral H, Demiral I, Tümsek F, Karabacakoglu B (2008) Adsorption of chromium (VI) from aqueous solution by activated carbon derived from olive bagasse and applicability of different adsorption models. Chemical Engineering Journal 144: 188-196.
- Pavan FA, Mazzocato AC, Gushikem Y (2008) Removal of methylene blue dye from aqueous solutions by adsorption using yellow passion fruit peel as adsorbent. BioresourTechnol 99: 3162-3165.
- Lagergren S (1898)Zurtheorie der sogenannten adsorption gelösterstoffe.
- Weber TW,Chakravorti RK (1974) Pore and solid diffusion models for fixed-bed adsorbers. AIChE Journal20: 228-238.
- Nuhoglu Y, Malkoc E (2009) Thermodynamic and kinetic studies for environmentaly friendly Ni(II) biosorption using waste pomace of olive oil factory. BioresourTechnol 100: 2375-2380.
- Weber W, Morris J (1963) Kinetics of adsorption on carbon from solution. J SanitEngDiv 89: 31-60.
- Boyd GE, Adamson AW, Myers LS Jr (1947) The exchange adsorption of ions from aqueous solutions by organic zeolites; kinetics. J Am ChemSoc 69: 2836-2848.
- Reichenberg D (1953) Properties of ion-exchange resins in relation to their structure. III. Kinetics of exchange. Journal of the American Chemical Society 75: 589-597.
- Dural MU, Cavas L, Papageorgiouc SK, Katsaros FK (2011) Methylene blue adsorption on activated carbon prepared fromPosidoniaoceanica(L.) dead leaves: Kinetics and equilibrium studies. Chemical Engineering Journal 168: 77-85.
- Milonjic SK (2007) A consideration of the correct calculation of thermodynamic parameters of adsorption. J Serb ChemSoc 72: 1363-1367.
- Rao MM , Rao GP, Seshaiah K, Choudary NV, Wang MC (2008) Activated carbon from Ceibapentandra hulls, an agricultural waste, as an adsorbent in the removal of lead and zinc from aqueous solutions. Waste Manag 28: 849-858.
- Mohammadi SZ, Karimi MA, Afzali D, Mansouri F (2010) Removal of Pb (II) from aqueous solutions using activated carbon from Sea-buckthorn stones by chemical activation. Desalination 262: 86-93.
- Giraldo-Gutiérrez L, Moreno-Piraján JC (2008)Pb (II) and Cr (VI) adsorption from aqueous solution on activated carbons obtained from sugar cane husk and sawdust. Journal of Analytical and Applied Pyrolysis 81: 278-284.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 19324
- [From(publication date):
May-2014 - Apr 07, 2025] - Breakdown by view type
- HTML page views : 14128
- PDF downloads : 5196