pKa Determination of a Non-hydro-soluble Chemical Substance, Issued from Chiral Chromatographic Solubility Profiles and Mat-pKa Calculations
Received: 25-Jan-2016 / Accepted Date: 12-Feb-2016 / Published Date: 19-Feb-2016 DOI: 10.4172/2155-9872.1000299
Abstract
After development and implementation of Mat-pKa software, since 3 years, pKa(s) determinations for approximately 70 compounds were successfully conducted. But a remaining objective was to enlarge the capabilities of this software to resolve cases for non-soluble compounds in aqueous phases. Until now, pKa(s) calculations were based on solubility profiles obtained in aqueous buffered solutions. A new application of this software was successful for solubility profiles obtained in pure water, in which, various concentrations of the substance led to different pH of solutions. A new approach, based on solubility profile elaborated from the Yasuda-Shedlovsky experiment, is presented in this paper, for a non-hydro-soluble chemical substance. More challenging in this case, the pKa value was determined for a chiral compound and, outside of the range 0 to 14. In this third new application, Mat-pKa software confirmed its ability to define pKa values in extended ranges and its independence to diverse techniques (generally the chromatography) delivering solubility profiles, even in very specific and delicate conditions.
Keywords: Mat-pKa; pKa determination; pKa of non-hydro-soluble chemical substances; Chromatography; Chiral chromatography; QSAR
302633Introduction
Background of Mat-pKa software creation
Specifically developed 3 years ago, Mat-pKa is a software for calculations of pKa(s) of chemical substances, based on their experimental solubility profiles. Since this time, approximately 70 molecules pre-candidates or candidates to the development have obtained their respective pKa(s) calculated with this software in our R&D environment. These calculations correspond to the resolution of the systems of equations governed by the expressions of the dissociation constants of each entity of the molecule tested, without any approximation, or introduction of additional parameters, or convergence factor, leading finally to the determinations of experimental pKa(s) depending only on the measured solubility and the measured pH of the solutions.
Validation and performances of this software have been provided and tested, as reported in the publication [1] related to the creation and the concept of these calculations. Comparisons with other calculations techniques, or other software have been scrutinized. A large comparative study on 41 molecules, including a predictive software, 2 dedicated experimental equipment and Mat-pKa was also provided.
This approach is of high interest, firstly because solubilities can be measured with different techniques (as Liquid Chromatography, Capillary Electrophoresis, UV spectrometry, or Potentiometry) and secondly because calculations of more than ten pKa(s) can be achieved in few seconds for one molecule, after the insertion of the needed couples of data (solubilities and pH(s) of the solutions). Another interest, is the difference with other software (ACD, VCC, Epik, Marvin, Pallas, Gastro-Plus, Pharma Algorithm and others), based on the structure recognition of moieties and their respective environment in the molecule, to generate empirical estimates (more or less accurate) of these pKa(s).
This new software presents also the advantage to be used on simple computers (PCs) equipped with Microsoft Office™ environment, because the code is written in Visual Basic and of course, don’t need link with experimental equipment.
The Table 1 illustrates the performance of the software compared to the dedicated techniques (Titration, UV, CE) and to ACD v12 software for some drug substances analyzed recently (2013).
| Compounds | Nb of pKas (identified functions) | pKas according to ACD v12 | Experimental pKas | pKas issued from Mat-pKa and solubility profile | Coherence with Mat-pKa |
|---|---|---|---|---|---|
| Compound 1 | 4 | 1.66 | 2.7 | 2.7 | Exp ↔ Mat-pKa |
| 6.28 | 5.32 | ACD ↔ Mat-pKa | |||
| 7.76 | 7.6 | 6.07 | Exp ↔ Mat-pKa | ||
| 12.68 | 11.69 | ACD ↔ Mat-pKa | |||
| Compound 2 | 4 | -1.38 | -1.86 | ACD ↔ Mat-pKa | |
| 2.81 | 0.71 | No coherence | |||
| 5.17 | 5.2 | 5.44 | ACD ↔ Exp ↔ Mat-pKa | ||
| 12.21 | 12.2 | ACD ↔ Mat-pKa | |||
| Compound 3 | 1 | 0.42 | 3 | 3.2 | Exp ↔ Mat-pKa |
| Compound 4 | 4 | -1.52 | 2.42 | No coherence | |
| 6.03 | 6.4 | 7.3 | ACD ↔ Exp ↔ Mat-pKa | ||
| 9.66 | 9.3 | 9.23 | ACD ↔ Exp ↔ Mat-pKa | ||
| 11.95 | 11.91 | ACD ↔ Mat-pKa | |||
| Compound 5 | 3 | -1.67 | 3.34 | No coherence | |
| 8.93 | 8.62 | 8.85 | ACD ↔ Exp ↔ Mat-pKa | ||
| 11.89 | 11.3 | ACD ↔ Mat-pKa | |||
| Compound 5 (Salified) | 3 | -1.67 | -0.27 | No coherence | |
| 8.93 | 8.62 | 8.31 | ACD ↔ Exp ↔ Mat-pKa | ||
| 11.89 | 13.1 | ACD ↔ Mat-pKa |
Table 1: Comparative table of pKa(s) determinations for 6 substances in 2013.
This table demonstrates clearly, the better capabilities of Mat-pKa to determine the pKa(s) of these molecules, compared to the dedicated techniques which, most of the time, were not able to provide all the expected values. We can also point out here, the performance of the software when the pKa(s) values are less than 2.5 or more than 9.5. In the light of the example of the Compound 1, Mat-pKa has resolved 2 pKa(s) values, which are close from each other (5.32 and 6.07).
Frequently, results of ACDv12, experimental determinations and Mat-pKa calculations are not too far from each other. Some noncoherences are observed between Mat-pKa and ACDv12, for very low pKa(s) values (considering ACD v12 as the reference).
More recently in 2014, new extensions of Mat-pKa capabilities were evidenced. A simultaneous determination of 4 (or 5) pKas, of one chemical substance and its organic salt was achieved in specific conditions. In this case the solubility profile was determined in pure water, by applying different concentrations of this compound for different generated pH of solutions.
Until now these solubility profiles were managed in aqueous buffered solutions. 2 pKas were attributed to the substance and 2 others were attributed to the organic counter-ion. And finally, a fifth pKa was also determined for one impurity generated in water (and not fully stable in the analytical conditions).
Objectives of the study
The concept of this study was put in place to resolve the determination of one pKa, for a chemical substance bearing a thiazole ring, as a weak base. Environment of this ring in the chemical structure was also suspected to play a role in the activation or the deactivation of this weak base. Evaluation of pKa was processed through the ACD 2014 software suite (Percepta). The result based on the structure of the compound conducted to the pKa value estimated to 1.9 for the amine ring moiety. This low pKa value suggested that classical dedicated techniques, as for instance, Capillary Electrophoresis coupled to Ultra- Violet detection, or acido-basic titrations by potentiometry [2] or Ultra-Violet detections [3,4], or combined analytical determinations in cases of multi-protic compounds [5] will be very limited to reach an experimental determination of this dissociation constant. This aspect is the first disadvantage for this chemical substance.
Familiarized with the Mat-pKa software over the 3 last years, leading to pKa(s) determinations without any limitation in the pKa range, the idea was to submit the solubility profile of this very weak base to these pKa calculations. But, as a second disadvantage, the chemical structure of this compound reveals 2 chiral centers, leading to 4 possible enantiomers. Consequently, the analytical method, to be used for the measurements of the solubility profile, must be selective for these chiral aspects, to be sure to quantify the contents of the right enantiomer. Of course, the chiral chromatography technique will be the best appropriate method.
Finally, as a third disadvantage, the solubility of this compound in aqueous buffered solutions was very poor, leading to results below the limit of quantitation (LOQ) of the analytical method and non-exploitable by Mat-pKa software. To resolve this last issue, improvements of the solubility in mixtures of organic solvent and aqueous buffered solutions must be studied. This last approach is identical to the one developed by Yasuda-Shedlovsky [6,7] and applied since a long time by many users.
Consequently the concept of this study was established on the following processes:
- Development and validation (most relevant parameters) of a selective chiral chromatographic method.
- Design of the protocol, for a direct application of the Yasuda- Shedlovsky method, with the selection of different mixtures of organic solvents and water (in this case, buffered solutions), for which dielectric constants are known and pH of the solutions can be measured.
- Calculations of the psKa values (pKa in organic/water solvents) for each mixture, using the Mat-pKa software.
- Extraction of the pKa value of the compound (at 100% of water, ε=80.65), using the linear relation between psKa and the dielectric constant ε, proposed by Yasuda-Shedlovsky:
psKa + log([H2O]) =α / ε + b
Development and validation of the chiral chromatographic method
As chromatographic chiral separation conditions are not predictable, with any specific rules to anticipate if the separation will succeed, a chiral chromatographic analytical screening is necessary. During this screening we test different chiral stationary phases available and usable at the analytical but also at the preparative chromatography scale, combined in a fully automated experimental mode with different mobile phases, leading to a total of more than 60 possible combinations. We perform this screening on analytical HPLC (High Performance Liquid Chromatography) and also on analytical SFC (Supercritical Fluid Chromatography) because these separation techniques are used in a complementary manner in our laboratories.
After this screening step, we chose the best technique HPLC or SFC and the best chiral stationary phase combined with the best mobile phase for chiral analysis or for preparative chromatography. In this paper, only the optimized method is reported for the analytical quantification of the 4 enantiomers, but we have also developed a method and we have performed the separation of each enantiomer using chiral HPLC preparative chromatography.
Design of the protocol for the Yasuda-Shedlovsky experiments
The protocol was designed according to the following experimental needs:
-4 series of (organic/aqueous buffers) solvent mixtures, respectively, 20/80, 40/60, 60/40 and 80/20 (%v/v). The solution of the chemical substance dissolved in Acetonitrile (~2 mg/mL) was considered as the organic phase.
-6 series of aqueous buffered solutions at expected pHs: 1.3, 3.0, 4.5, 6.4, 7.5 and 9.0. According to the literature (8), solubilities of these reagents at concentrations around 50 mM are compatible with these aqueous / acetonitrile mixtures.
- For each series of the 4 solvent mixtures (combined with each of the 6 buffered solution), ionic strengths to be maintained by addition of KCl solutions prepared at appropriate concentrations, to complete each final mixture to 10 mL.
-The chromatographic method retained to provide the concentrations of each solution was the one used for the chiral purity determination (see experimental section). Potential isomerization of the molecule cannot be excluded and the needs of the strong selectivity of this method might be appreciated in case of impurity formation.
-Sensitive pH-meter and its electrode (713 pH-meter Methrom, calibrated with reference buffered solutions at pH 3.0, 5.0 and 7.0 respectively) to make pH measurements in the mixtures described above.
-Mat-pKa software for the calculation of psKa + log([H2O]) noted psKa’
Experimental Section
Analytical method for chiral purity determination
The parameters of this method are given bellow:

As a remark the eluent, the stationary phase (cellulose tris(3,5 dimethylphenycarbamate) as chemical graft) and the detection wavelength are close to the ones used for the preparative HPLC method, developed for the isolation and the characterization of each enantiomer.
Validation of the analytical method for chiral purity determination
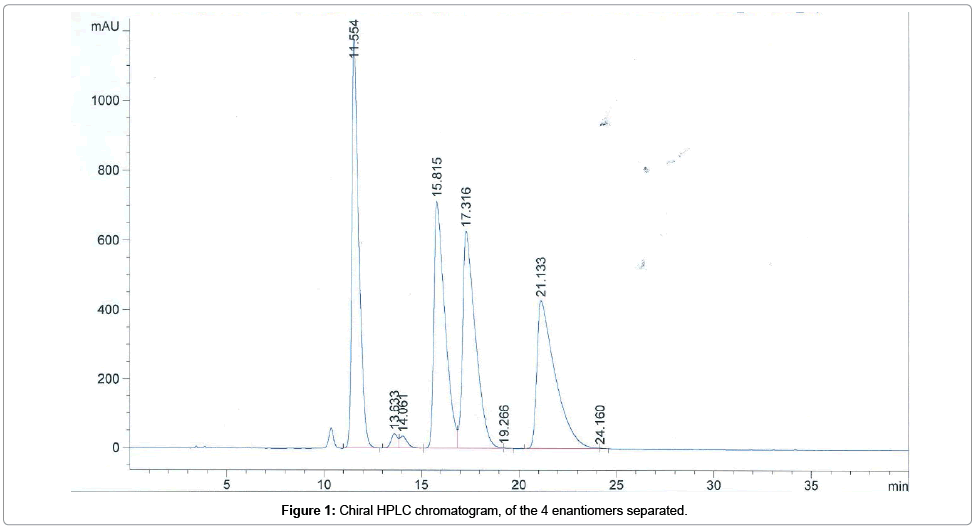
Selectivity of the method: The selectivity of the method was validated based on the analysis of the reference sample, corresponding to a mixture of the 4 enantiomers of the chemical substance. As shown in Figure 1, the 4 enantiomers are separated with a high resolution, particularly the last peak eluted corresponding to the substance studied.
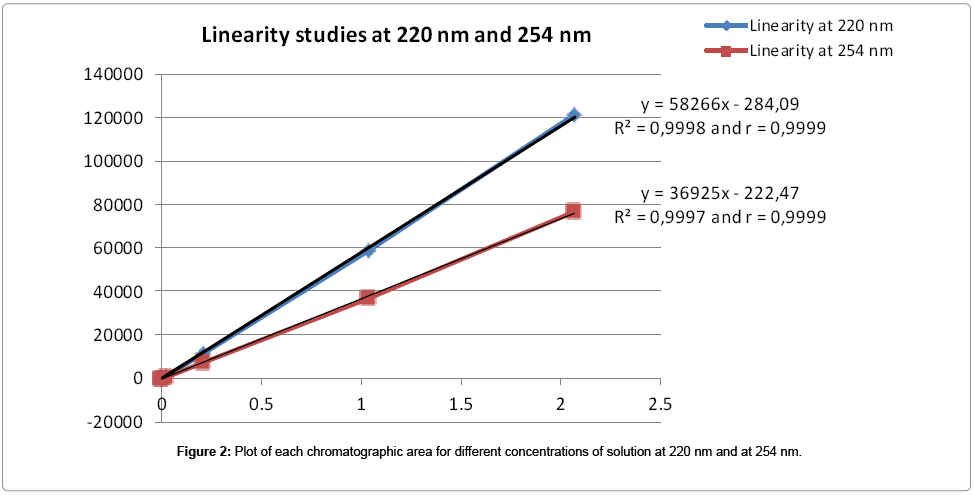
Linearity of the UV response of the method: Six solutions at 0.05% - 0.1% - 1% - 10% - 50% - 100% of the working concentration (2 mg/mL) of the substance were prepared by dilution of the 100% stock solution. One chromatogram of each solution was recorded (Table 2). The graphic presentation of the peaks areas obtained for these solutions versus their respective concentrations is represented in Figure 2.
| Concentration % | 0.05 | 0.1 | 1 | 10 | 50 | 100 |
|---|---|---|---|---|---|---|
| Concentration mg/ml | 0.0001 | 0.0021 | 0.0208 | 0.2071 | 1.0353 | 2.0706 |
| Area (inj 30 µl) at 254 nm | 9.11 | 36.68 | 707.28 | 7345.85 | 37067.1 | 76710.4 |
| Area (inj 30 µl) at 220 nm | 42.2 | 135.91 | 1185.82 | 11681.6 | 58565.2 | 121105 |
Table 2: Linearity study results.
The values obtained for the 2 correlation coefficients (=0.9999) demonstrated the linearity of UV response for the compound in the range of concentrations studied, at 220 nm and at 254 nm.
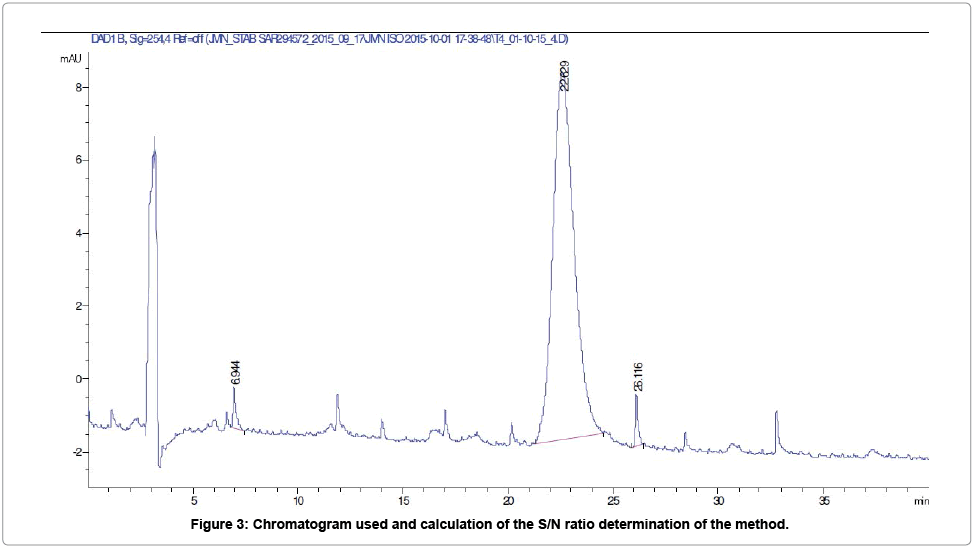
Limit of quantification: Based on the signal to noise ratio (S/ N=16.4) obtained for the solution concentrated at 1% (Figure 3) and taking into account the demonstration of the linearity of the method, the limit of quantification (LOQ) was recalculated and was estimated to 12.63 μg/ml (0.6%).
Peaks marked with a retention time value, were not included in the evaluation of the height of the noise of the chromatogram. The height of the peak, at retention time 22.63 min, was taken into account for the calculation of the Signal to Noise ratio (according to the European Pharmacopea 2.2.46).
Protocols used for solubility measurements
The 6 buffered solutions and the potassium chloride solutions were prepared according the Table 3.
| Medium | Composition |
|---|---|
| HCl 0.05N (pH 1.3) | 10 mL of HCl 0.1N (Merck) adjusted to 20.0 mL with Millipore water. |
| Citrate buffer pH3 | Solution A is prepared with 267.9 g of citric acid monohydrated (VWR, ref: 20276.292) in 20 mL of Millipore water. Solution B is prepared with 595.9 mg of citric trisodium dihydrated salt (VWR ref: 27830.294) in 40 mL of Millipore water. Solution B is added to solution A to adjust the pH to 3.0. |
| Acetate buffer pH 4.5 | Anhydrous sodium acetate (Fisher ref: S/210/50) 96.88 mg + 1 drop of acetic acid. pH 4.5 is adjusted in this solution by addition of diluted acetic acid (1:10). Solution completed to 20.0 mL with Millipore water. |
| Phosphate buffer pH 6.5 | 3.2 mL K2HPO4 0.1M (Merck ref: 1.5099 - 279.8 mg in 20 mL of Millipore water) + 6.8 mL KH2PO4, 3H2O 0.1M (Fisher ref: P/5320/53 - 484.9 mg in 20 mL of Millipore water) solution adjusted to 20.0 mL with Millipore water. |
| Phosphate buffer pH 7.4 | 1.9 mL of K2HPO4 0.1M (Merck ref: 1.5099 - 279.8 mg in 20 mL of Millipore water) + 8.1 mL of KH2PO4, 3H2O 0.1M (Fisher ref: P/5320/53 - 484.9 mg in 20 mL of Millipore water) solution adjusted to 20.0 mL with Millipore water. |
| Trishydroxymethylaminomethane pH 9.0 buffer | 163.3 mg of Trishyroxymethylaminomethane (Fisher ref: T395.500) in 20 ml of Millipore water. Add 140 μl of HCl 1N and adjust to pH to 9.0 with HCl 0.1N. Dilute to 40 ml with Millipore water. |
| Solution of KCl (a) - 0.061M | 15 mL of solution (c) adjusted to 20 mL |
| Solution of KCl (b) - 0.041M | 10 mL of solution (c) adjusted to 20 mL |
| Solution of KCl (c) - 0.082M | 607.2 mg of Potassium Chloride (Merck ref: 1.59707) dissolved in Millipore water and adjusted to 100 mL |
Table 3: Preparation of aqueous buffered solutions and potassium chloride solutions.
These aqueous solutions were added to the organic solution of the chemical substance studied, according to the Table 4. In which, Ci corresponds to the concentration of each species present in the considered solution and zi the charge of this species. Concentrations of species in buffered solutions (phosphate, acetate, citrate and trishydroxymethylammoniummethane) were extracted from Mat-pKa software according to each measured pH and the respective pKas of each species. As this can be observed in the Table 4 the ionic strength of each mixture of organic solvent /water was maintained approximately at the same level. Before analysis, each solution was filtered on a 0.22 μ GHP filter.
| Compound solution, 2 mg/mL in CH3CN | Aqueous buffered solutions | Aqueous buffered solutions | Aqueous KCl solutions | Aqueous KCl solutions | Organic composition | Dielectric constants of mixtures | Total ionic strengths* |
|---|---|---|---|---|---|---|---|
| Volume (mL) | pH | Volume (mL) | (M) | Volume (mL) | (% v/v) | (ε) | (M) |
| 2.0 | 1.32 | 4.0 | 0.061 | 4.0 | 20 | 73.2 | 0.044 |
| 2.0 | 3.17 | 4.0 | 0.081 | 4.0 | 20 | 73.2 | 0.045 |
| 2.0 | 4.23 | 4.0 | 0.041 | 4.0 | 20 | 73.2 | 0.068 |
| 2.0 | 6.18 | 4.0 | 0.041 | 4.0 | 20 | 73.2 | 0.041 |
| 2.0 | 7.08 | 4.0 | 0 | 4.0 | 20 | 73.2 | 0.040 |
| 2.0 | 8.99 | 4.0 | 0.082 | 4.0 | 20 | 73.2 | 0.037 |
| 4.0 | 1.32 | 3.0 | 0.061 | 3.0 | 40 | 64.75 | 0.033 |
| 4.0 | 3.17 | 3.0 | 0.081 | 3.0 | 40 | 64.75 | 0.034 |
| 4.0 | 4.23 | 3.0 | 0.041 | 3.0 | 40 | 64.75 | 0.051 |
| 4.0 | 6.18 | 3.0 | 0.041 | 3.0 | 40 | 64.75 | 0.031 |
| 4.0 | 7.08 | 3.0 | 0 | 3.0 | 40 | 64.75 | 0.030 |
| 4.0 | 8.99 | 3.0 | 0.082 | 3.0 | 40 | 64.75 | 0.028 |
| 6.0 | 1.32 | 2.0 | 0.061 | 2.0 | 60 | 54.6 | 0.022 |
| 6.0 | 3.17 | 2.0 | 0.081 | 2.0 | 60 | 54.6 | 0.022 |
| 6.0 | 4.23 | 2.0 | 0.041 | 2.0 | 60 | 54.6 | 0.034 |
| 6.0 | 6.18 | 2.0 | 0.041 | 2.0 | 60 | 54.6 | 0.021 |
| 6.0 | 7.08 | 2.0 | 0 | 2.0 | 60 | 54.6 | 0.020 |
| 6.0 | 8.99 | 2.0 | 0.082 | 2.0 | 60 | 54.6 | 0.019 |
| 8.0 | 1.32 | 1.0 | 0.061 | 1.0 | 80 | 45.55 | 0.011 |
| 8.0 | 3.17 | 1.0 | 0.081 | 1.0 | 80 | 45.55 | 0.011 |
| 8.0 | 4.23 | 1.0 | 0.041 | 1.0 | 80 | 45.55 | 0.017 |
| 8.0 | 6.18 | 1.0 | 0.041 | 1.0 | 80 | 45.55 | 0.010 |
| 8.0 | 7.08 | 1.0 | 0 | 1.0 | 80 | 45.55 | 0.010 |
| 8.0 | 8.99 | 1.0 | 0.082 | 1.0 | 80 | 45.55 | 0.009 |
*: total ionic strengths of the media were calculated according to the following formula: 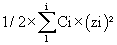
Table 4: Prepared solutions for solubility measurements.
Results
The Table 5 shows all the couples of data (Calc. concentrations=f(pH)) needed to launch calculation with the MatpKa software.
In this table some calculated concentrations are above the maximum values acceptable (bolded). Origins of these abnormalities were investigated and attributed to the non-perfect sealing of the bottles containing the prepared mixtures and or vials for chromatography. In these cases evaporation of the solvents, mainly of the acetonitrile, and consequently increases of concentration of these solutions were observed. Due to the limited quantities of the chemical substance available, these experiments have not been re-processed.
psKa’ determination using Mat-pKa, for 40% of acetonitrile co-solvent
The series of results concerned for these calculations with Mat-pKa, are extracted from the Table 5 corresponding to 40% v/v (2nd series of 6 values in this table).
| Measured pH after filtration | Area at 254 nm | Max conc. (mg/mL) | Calculated conc. (mg/mL)* | Organic Composition (% v/v) |
|---|---|---|---|---|
| (Reference solution) 76710.4 | 2.0706 | 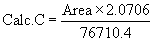 |
100 | |
| 1.67 | N.D. | 0.41412 | N.A. | 20 |
| 3.44 | N.D. | 0.41412 | N.A | 20 |
| 4.59 | N.D. | 0.41412 | N.A | 20 |
| 6.59 | N.D. | 0.41412 | N.A | 20 |
| 7.52 | N.D. | 0.41412 | N.A | 20 |
| 8.87 | N.D. | 0.41412 | N.A | 20 |
| 1.68 | 25174.6 | 0.82824 | 0.67952359 | 40 |
| 3.76 | 21617.7 | 0.82824 | 0.58351423 | 40 |
| 5.09 | 3638.7 | 0.82824 | 0.09821735 | 40 |
| 6.91 | 23964.3 | 0.82824 | 0.64685466 | 40 |
| 7.83 | 27001.6 | 0.82824 | 0.72883876 | 40 |
| 8.79 | 9991.9 | 0.82824 | 0.26970565 | 40 |
| 1.64 | 45766 | 1.24236 | 1.23533549 | 60 |
| 4.01 | 55100.4 | 1.24236 | 1.48729362 | 60 |
| 5.57 | 48839.9 | 1.24236 | 1.31830752 | 60 |
| 7.13 | 56260 | 1.24236 | 1.51859404 | 60 |
| 8.12 | 45295.7 | 1.24236 | 1.22264095 | 60 |
| 8.71 | 54546.4 | 1.24236 | 1.47233981 | 60 |
| 1.42 | 60618.9 | 1.65648 | 1.63625133 | 80 |
| 4.35 | 59978.1 | 1.65648 | 1.61895459 | 80 |
| 6.36 | 60287.6 | 1.65648 | 1.62730874 | 80 |
| 7.35 | 64006.8 | 1.65648 | 1.72769898 | 80 |
| 8.51 | 59231.4 | 1.65648 | 1.59879934 | 80 |
| 8.57 | 84731.6 | 1.65648 | 2.28711167 | 80 |
Table 5: Solubility results of the chemical substance in different mixtures of solvents and at different pH.
Mat-pKa calculations were conducted with the couples of data reported in Table 6. Mat-pKa software results are reported in the Table 7.
| Measured pH after filtration | Calculated conc. (mg/mL) |
|---|---|
| 1.68 | 0.67952359 |
| 3.76 | 0.58351423 |
| 5.09 | 0.09821735 |
| 6.91 | 0.64685466 |
| 7.83 | 0.72883876 |
| 8.79 | 0.26970565 |
Table 6: Solubility/pH of solutions used for psKa’ calculation of the chemical substance, in 40% of acetonitrile.
| Experimental results (Solubility in mg/mL) - Chemical Substance (40% CH3CN) | ||||||
|---|---|---|---|---|---|---|
| pH | 1.68 | 3.76 | 5.09 | 6.91 | 7.83 | 8.79 |
| Solubility | 0.6795 | 0.5835 | 0.0982 | 0.6469 | 0.7288 | 0.2697 |
| Nb of acid functions | 1 | |||||
| pKas | pKa1 | |||||
| ACD (Percepta) | 1.9 | |||||
| Calculated results (Solubility in mg/mL and pKas) | ||||||
| Entity considered | HA | A | ||||
| Intrinsic solubility | N.A. | 0.58269481 | ||||
| pKa1 | Ka <0 | 0.90045749 | ||||
Table 7: Extraction of the Mat-pKa table of results (chemical substance in 40% of acetonitrile).
According to the Table 7, psKa’ of the chemical substance, in a mixture of 40% acetonitrile and 60% of water, was calculated to 0.9 by Mat-pKa. Only one psKa’ was accessible through these calculations. The entity governing the solubility of the substance in this medium, is clearly the neutral molecule (A in the table), which corresponds to a very weak base, according to the low value of this psKa’ of the conjugated acid.
The Table 8 and the curve (Figure 4) show the acceptable correlation of the experimental solubility results plotted with red points, with the ones issued from the psKa’ calculation (dark blue curve).
| Measured pH | 1.68 | 3.76 | 5.09 | 6.91 | 7.83 | 8.79 |
| Measured solubility | 0.6795 | 0.5835 | 0.0982 | 0.6469 | 0.7288 | 0.2697 |
| Re-calculated solubility (Mat-pKa) | 0.6751# | 0.5834# | 0.5827 | 0.5827* | 0.5827* | 0.5827 |
Results highlighted with # indicates values in the range ± 10%; Results highlightedwith * indicates values in the range ± 30%; Results highlighted in italics indicates values in the range ± 100%
Table 8: Experimental and re-calculated solubilities of the compound in 40% of CH3CN co-solvent
psKa’ determination using Mat-pKa, for 60% of acetonitrile co-solvent
The series of results concerned for these calculations with Mat-pKa, are extracted from the Table 5 corresponding to 60% v/v (3rd series of 6 values in this table). As it is reported, 4 solubility values were obtained above the maximum possible solubility (in this case, 1.2424 mg/mL).
Consequently these 4 couples of data were not included in the calculations with Mat-pKa. Fortunately the 2 last couples of data (at pH 1.64 and pH 8.12) presented concentration profiles eligible for one psKa’ determination, as presented in the Table 9. Mat-pKa software results are reported in the Table 10.
| Measured pH after filtration | Calculated conc. (mg/mL) |
|---|---|
| 1.64 | 1.23533549 |
| 8.12 | 1.22264095 |
Table 9: Solubility/pH of solutions used for psKa’ calculation of the chemical substance, in 60% of acetonitrile
| Experimental results (Solubility in mg/mL) - Chemical Substance (60% CH3CN) | ||||
|---|---|---|---|---|
| pH | 1.64 | 8.12 | ||
| Solubility | 1.2353 | 1.2226 | ||
| Nb of acid functions | 1 | |||
| pKas | pKa1 | |||
| ACD (Percepta) | 1.9 | |||
| Calculated results (Solubility in mg/mL and pKas) | ||||
| Entity considered | HA | A | ||
| Intrinsic solubility | N.A. | 1.2226 | ||
| pKa1 | Ka <0 | -0.34348053 | ||
Table 10: Extraction of the Mat-pKa table of results (chemical substance in 60% of acetonitrile).
According to the Table 10, psKa’ of the chemical substance, in a mixture of 60% acetonitrile and 40% of water, was calculated to -0.34 by Mat-pKa. The entity governing the solubility of the compound in this medium, is again the neutral molecule (A in the table), which is a very weak base, according to the low value of this psKa’ of the conjugated acid. This observation confirms the previous one, issued from the experiment conducted with 40% (v/v) of acetonitrile. We can observe also that the intrinsic solubility is not too far from the maximum concentration of the solutions prepared for this experiment.
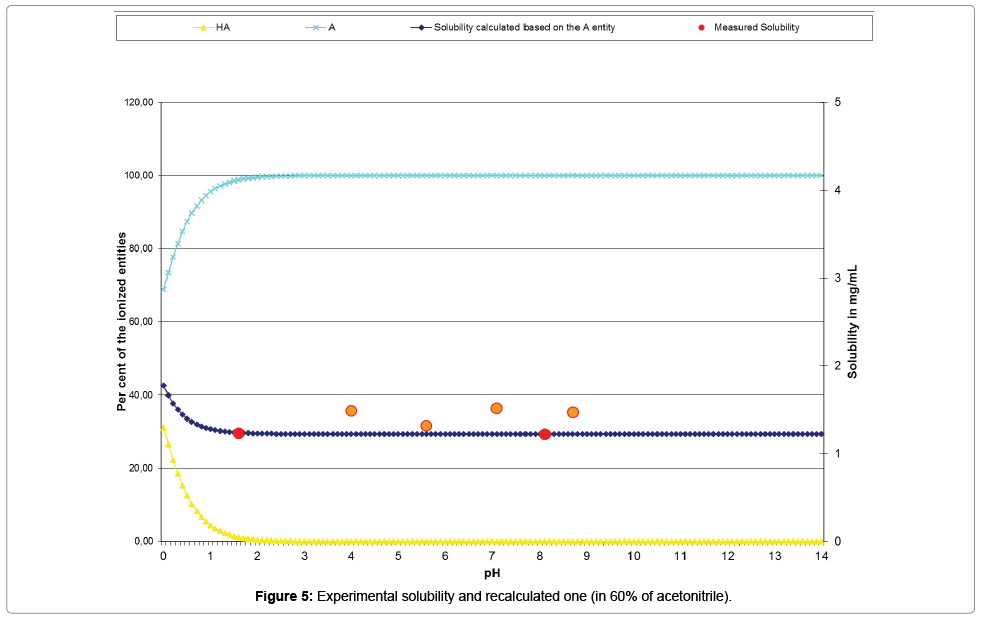
The Table 11 and the curve (Figure 5) show the acceptable correlation of the experimental solubility results plotted with red points and orange points (for those excluded from the calculations), with the ones issued from the psKa’ calculation (dark blue curve).
| Measured pH | 1.64 | 4.01 | 5.57 | 7.13 | 8.12 | 8.71 |
| Measured solubility | 1.2353 | 1.4873 | 1.3183 | 1.5186 | 1.2226 | 1.4723 |
| Re-calculated solubility (Mat-pKa) | 1.2365# | 1.2227* | 1.2226# | 1.2226* | 1.2226# | 1.2226* |
Results highlighted with # indicates values in the range± 10%; Results highlighted with * indicates values in the range ± 30%; Results highlighted in italics indicates measured values over the maximum possible (indicating their increases of concentration during the experimental process)
Table 11: Experimental and re-calculated solubilities of the chemical substance in 60% of CH3CN co-solvent.
psKa’ determination using Mat-pKa, for 80% of acetonitrile co-solvent
The series of results concerned for these calculations with Mat-pKa, are extracted from the Table 5 corresponding to 80% v/v (4th series of 6 values in this table). As it is reported, 2 solubility values were obtained above the maximum possible solubility (in this case, 1.6565 mg/mL).
Consequently these 2 couples of data were not included in the calculation with Mat-pKa. Fortunately, the 4 last couples of data (at pH 1.42, pH 4.35, pH 6.36 and pH 8.51) were used for psKa’ determination, as this is reported in the Table 12. Mat-pKa software results are reported in Table 13.
| Measured pH after filtration |
Calculated conc. (mg/mL) |
|---|---|
| 1.42 | 1.63625133 |
| 4.35 | 1.61895459 |
| 6.36 | 1.62730874 |
| 8.51 | 1.59879934 |
Table 12: Solubility/pH of solutions used for psKa’ calculation of the chemical substance, in 80% of acetonitrile.
| Experimental results (Solubility in mg/mL) - Compound (80% CH3CN) | ||||
|---|---|---|---|---|
| pH | 1.42 | 4.35 | 6.36 | 8.51 |
| Solubility | 1.6363 | 1.619 | 1.6273 | 1.599 |
| Nb of acid functions | 1 | |||
| pKas | pKa1 | |||
| ACD (Percepta) | 1.9 | |||
| Calculated results (Solubility in mg/mL and pKas) | ||||
| Entity considered | HA | A | ||
| Intrinsic solubility | N.A. | 1.61897965 | ||
| pKa1 | Ka <0 | -0.55068474 | ||
Table 13: Extraction of the Mat-pKa table of results (chemical substance in 80% of acetonitrile).
According to the Table 13, psKa’ of the chemical substance, in a mixture of 80% acetonitrile and 20% of water, was calculated to -0.55 by Mat-pKa. The entity governing the solubility of compound in this medium, is again the neutral molecule (A in the table), which is a very weak base, according to the low value of this psKa’ of the conjugated acid. This last calculation confirms the 2 others previously obtained in 40% and 60% (v/v) of acetonitrile. The intrinsic solubility value is also comparable to maximum concentration of the solutions prepared for this experiment.
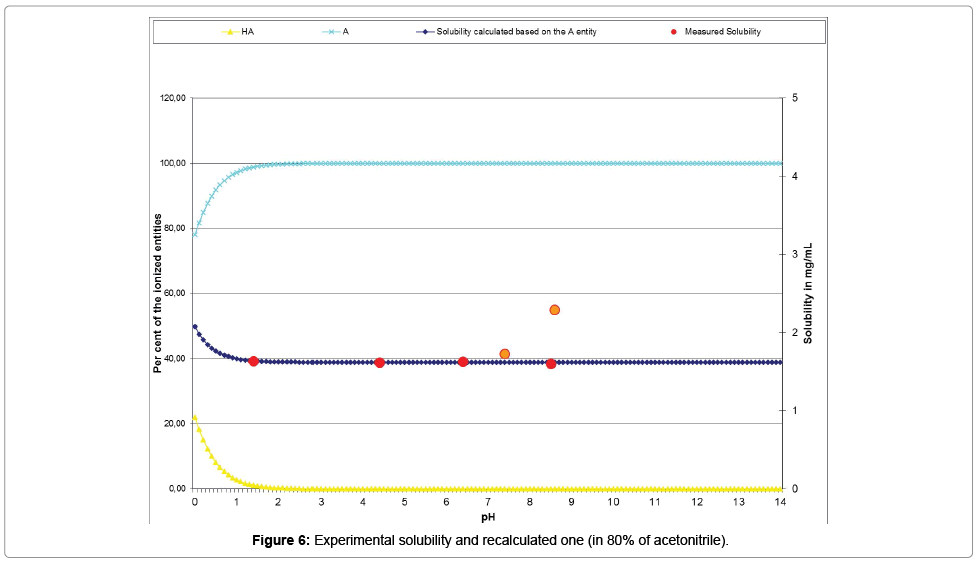
The Table 14 and the curve (Figure 6) present the acceptable correlation of the experimental solubility results plotted with red points and orange points (for those excluded from the calculations), with the ones issued from the psKa’ calculation (dark blue curve).
| Measured pH | 1.42 | 4.35 | 6.36 | 7.35 | 8.51 | 8.57 |
| Measured solubility | 1.6353 | 1.619 | 1.6273 | 1.7277 | 1.599 | 2.2871 |
| Re-calculated solubility (Mat-pKa) | 1.6371# | 1.6190# | 1.6190# | 1.6190# | 1.6190# | 1.6190* |
Results highlighted with # indicate values in the range ±10%; Results highlighted with * indicate values in the range ±100%; Results highlighted in italics indicate measured values over the maximum possible (indicating their increases of concentration during the experimental process)
Table 14: Experimental and re-calculated solubilities of the chemical substance in 80% of CH3CN co-solvent
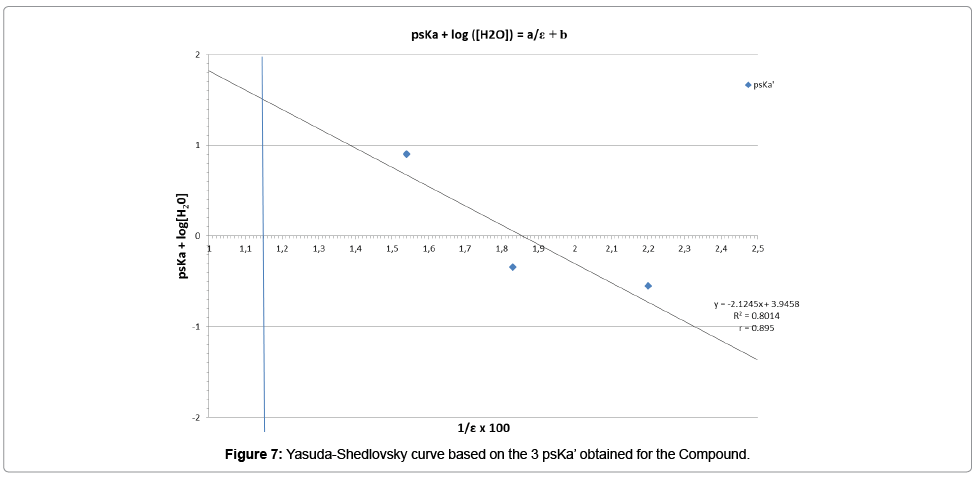
pKa determination with the series of psKa’ issued from the 3 mixtures of acetonitrile with water
Having in hands the 3 psKa’ of the chemical substance, obtained in 3 different binary solvents for which each dielectric constant is known, the linear Yasuda-Shedlovsky extrapolation can be tested. The Table 15 summarizes the data that should be taken into account.
| psKa’ isuued from Mat-pKa | Organic composition (% V/V) | Dielectric Constant (ε) | 1/ε | Log ([H2O])=Log (55.508) |
|---|---|---|---|---|
| 0.900 | 40 | 64.75 | 0.0154 | 1.744 |
| -0.345 | 60 | 54.6 | 0.0183 | 1.744 |
| -0.551 | 80 | 45.55 | 0.0220 | 1.744 |
Table 15: Summarized data for Yasuda-Shedlovsky linearity calculation.
The linear regression reported on the curve (Figure 7) was obtained with a correlation coefficient around 0.9, which is probably perfectible, due to the point at ε=54.6 (1/ε=0.0183) for which the psKa’ was determined only with 2 couples of experimental points.
According to Yasuda-Shedlovsky method, the negative slope of the curve indicates that we are in presence of a base, as this was also confirmed by Mat-pKa (Tables 7, 10 and 13). Based on the equation of this curve, the extrapolated value at 1/ε=0.0124 (100% of water), leads to a dissociation constant of the conjugated acid function of the molecule:
pKa=-0.43
For a simple evaluation, if the second point of this curve is not included in the linearity study, then the pKa value is -0.19, finally not too far from the retained value.
The pKa value (-0.43) is far from the one suggested by ACD 2014 (pKa=1.9). But it confirms the added effects of the environment of the thiazole ring of the molecule, in terms of steric constraints and increase of the delocalization of the free doublet of electrons of the nitrogen atom in the conjugated bonds. On a practical point of view this pKa result confirms also, the difficulties encountered to synthesize a salt, with this very weak base.
Discussion
Influence of the organic solvent and of the aqueous buffered pH on the solubility of the chemical substance
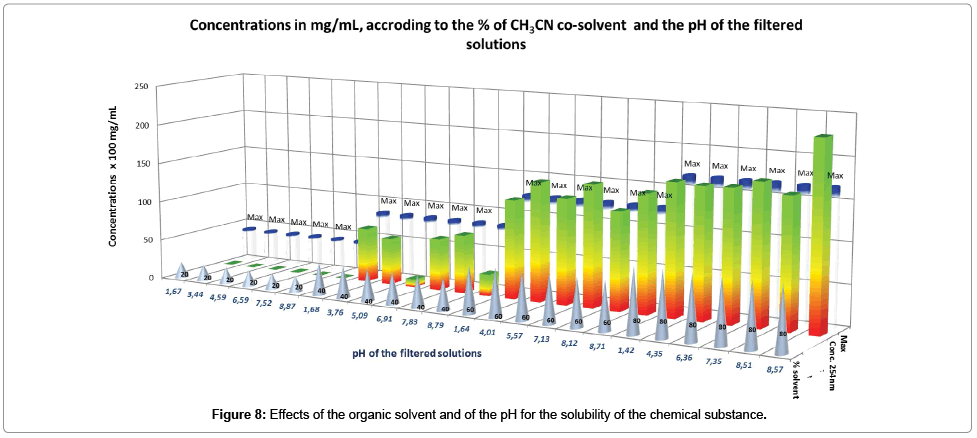
Taking into account the assay provided for each solution (Table 5), the following global effects are pointed out through the interpretation of the Figure 8.
It is evidenced that the increase of the organic solvent proportion, increases considerably the solubility of the chemical substance, to be equal to the maximum when the proportion of acetonitrile starts at 60%. At this level of co-solvent mixture, the influence of pH variation is very limited, suggesting that the non-protonated molecule is preferably solubilized in acetonitrile, consequently away from the effects of protons, which stayed separately in the aqueous solution.
On the other hand, insolubility of the chemical substance is observed between 0% and 20% of acetonitrile mixed with water, whatever the pH value, suggesting its moderate effect. These series of data cannot be exploited with Mat-pKa. Regarding the series of solubilities with 40% of acetonitrile, where values are lower than the maximum, it seems that the pH of the solution has an effect, confirming that, impact of this parameter takes place after the first of the organic organic solvent. In this series, we should notice that the solubility is limited at pH 5.09 and pH 8.79.
Interesting points of enhanced solubility with 40% of acetonitrile are between pH 1.68 and pH 3.76 (compatible with stomach environment) and between pH 6.91 and pH 7.83 (compatible with fasted intestine and plasma environment).
As a first result of this experiment, the drug substance formulated with excipients leading to an equivalent dielectric constant (ε) between 56.4<ε<64.75 (obtained in our case, with 40% to 60% of acetonitrile in water), should play an important role in the enhancement of the bioavailability of the compound, by increasing its solubility and by maintaining its sensitivity to pH for the transportation. As a second result, we should notice that no racemization and no degradation of the molecule were observed in the solutions tested.
Mat-pKa software performance for this particular study
The Yasuda-Shedlovsky experiment is extensively used for the determination of pKas for insoluble compounds in aqueous media. Most of the time, it is associated to potentiometric titrations (or pHmetric titrations) of the substance of interest, to determine the inflexion points of the different curves and then the psKa related to each organic/ water composition [8-10]. UV titrations are also frequent [11] and psKa are determined based on absorbance responses obtained in different mixtures of organic solvents and pH buffered solutions. Other initiatives were also largely developed to use capillary electrophoresis (CE), by addition of co-solvents in case of insoluble substances [12].
In these cases, psKa(s) are also issued from sigmoidal curves representing the ion mobilities observed versus the pHs applied.
Liquid chromatography technique was also developed to obtain pKas of molecules, but based on the variations of their retention time (as this is also used for the logDpH determination) when submitted to different buffered eluents [13]. Another way was to determine separately logP and logDpH, from which pKa can be calculated [14], but apparently limited to one pKa per molecule.
But all of these initiatives are dependent on the capabilities to prepare aqueous buffered solutions (or to obtain them from the market) and of the corrosion resistance of the equipment, which finally are limiting the experimental pH range approximately between pH 2.5 to pH 10. This is a major concern when pKa values must be determined out of this range and particularly in the case of very weak bases, leading to pKas of conjugated acids between -2 and 1.5 for instance.
None of the constraints of methodologies or experiments mentioned above is affecting the pKa(s) determinations with MatpKa. And the particular case of the chiral chromatographic method used in this study reveals an extended capability of this software to be independent of the technics used, except the needs of concentrations of the substance and pH of the solution.
The principal advantage of Mat-pKa software is based on the determination of unknown pKas driving the solubility curve in extended pH points, avoiding the detection of inflexion points, as this is the case for the major part of the dedicated techniques. This software consists in the resolution of systems of equations of Henderson- Hasselbalch [15], without any approximation. Calculations conducted in few seconds, can deliver a high number (N) of pKas for one molecule, depending on the availability of (N+1) couples of data of solubility/pH. As a result, these calculated values can be determined, outside of the range of experimental pH of buffered solutions. Also, these pKa(s) can be evaluated even if they are spaced or very close to each other.
The particular case of the chemical substance studied here demonstrates clearly the performance of the Mat-pKa software, which generated psKa’ values between 0.9 and -0.55. No other techniques mentioned above would have been able to provide such results, either by Titration or UV spectrometry. Titration would have been limited by the needed concentration of the acid reagent to reach the efficient protonation of the amine and the equivalent point determination. UV spectrometry would have also been limited by the pH buffer preparation at negative pH. By the way, it is important to precise here, the prerequisites of the molecule to be sensitive to changes in absorbance when submitted to pHs variations, otherwise the UV metric method cannot be applied [13]. Finally, with these 2 methods, the 4 enantiomers of this chemical substance would have been analyzed as a mixture, which was not the objective of this study.
Considering the Capillary Electrophoresis, based on ions mobilities of the substance depending on the pH applied, we cannot exclude also the loss of the separation and the possible mixture for the 4 enantiomers in these variable and needed conditions to generate the appropriate data, exploited further to calculate the pKa of the molecule of interest. We should notice also, that a specific equipment (for instance, Combisep pKa analyser) and highest number of couples of data are needed (generally 12 different pH buffers, also limited between pH 2.0 to 10.0), compared to the 6 and less (4 and 2, in our non-voluntary cases) for Mat-pKa, with the maintained separation of the 4 enantiomers.
Similar interpretation can be conducted for some other chromatographic methods, also based on the variation of the retention time of the molecule analyzed, versus the pH of the mobile phase applied.
Conclusion
After 3 years of repetitive practices of the Mat-pKa software, several objectives have been completed. Now a new extension of Mat-pKa is available for pKa(s) determinations of chemical substances non-soluble in water, through the experiment of Yasuda-Shedlovsky.
This particular study succeeded due to the high selectivity of the chiral chromatographic method developed and validated, to maintain under control the quantitation of the good enantiomer. This is the first time that such a specific chiral chromatographic method is used for pKas determination. In this field of application Mat-pKa is probably the software the most appropriate to avoid the generation of titration curves (either by CE or HPLC) based on the retention time (or mobility) in function of the pH applied, with a high risk to lose the enantiomeric separations. By the way, Mat-pKa software needs less couples of data (meaning also time and quantities of compound) than the other methods, which needs titration curves and inflexion point determinations.
Finally, Mat-pKa has played its new role in these new particular conditions, to calculate the mandatory psKa’ needed for the pKa determination through the linear extrapolation of the Yasuda- Shedlovsky experiment. The pKa value of -0.43 determined for this chemical substance is lower than the predicted one (1.9 by ACD Predicta). It demonstrates a highest limitation of access to the free electronic doublet of the nitrogen atom of the molecule, than this was estimated by ACD.
The solubility profile of the chemical substance in different combinations of acetonitrile / water mixture and at different pHs, revealed clearly the following statements:
-between 0% to 20% (v/v) of acetonitrile in water, the chemical substance stayed insoluble
-Above 60% (v/v) of acetonitrile in water, the chemical substance was fully soluble without any effect of the pH
-At 40% (v/v) of acetonitrile in water, the chemical substance was approximately 75% soluble and pHs variations of the solutions have added a supplementary effect on the solubility and potential transport of the molecule in biological media.
These results, issued from the direct exploitation of the Yasuda- Shedlovsky experiment are also indicative for potential adjustments needed for the formulations of the chemical substance.
References
- Vidaud L, Kugel C, Boccardi G, Schmidt S, Pommier JY (2012) Mat-pKa calculation tool development for evaluation of acidity constants from solubility profiles- Large study of 41 compounds. Int J Pharm 437: 137-155.
- Martel AE, Motekaitis RJ (1992) Determination and Use of Stability Constants. In: Experimental procedure for Potentiometric pH measurements of Metal Complex Equilibria.
- Bates RG, Schwarzenbach G (1955) Über pH-Werte nichtwässeriger Lösungen. Helv Chim Acta 38: 699-716.
- Allen RI, Box KJ, Comer JEA, Peake C, Tam KY (1998) Multiwavelength Spectrophotometric Determination of Acid Dissociation Constants of Ionizable Drugs. J Pharm Biomed Anal 17: 699-712.
- Box KJ, Donkor RE, Jupp PA, Leader IP, Trew DF, et al. (2008) The chemistry of multi-protic drugs Part 1: a potentiometric, multi-wavelength UV and NMR pH titrimetric study of the micro-speciation of SKI-606. J Pharm Biomed Anal 47: 303-311.
- Yasuda M (1959) Dissociation Constants of Some Carboxylic Acids in Mixed Aqueous Solvents. Bull Chem Soc Jpn 32: 429-432.
- Shedlovsky T (1962) In: Pesce B (Ed) Electrolytes. Pergamon, New York, USA.
- Schellinger AP, Carr PW (2004) Solubility of Buffers in Aqueous-Organic Eluents for Reversed-Phase Liquid Chromatography. LCGC North America 22: 544-548.
- Demiralay EC, Yilmaz H (2012) Potentiometric pKa determination of Piroxicam and Tenoxicam in acetonitrile-water binary mixtures. SDU Journal of Science 7: 34-44.
- Avdeef A, Box KJ, Comer JEA, Gilges M, Hadley M, et al. (1999) pH-metric logP 11. pKa determination of water-insoluble drugs in organic solvent-water mixtures. J Pharm Biomed Anal 20: 631-641.
- Tam KY, Takacs-Novak K (2001) Multi-wavelength spectrophotometric determination of acid dissociation constant: a validation study. Analitica Chemica Acta 434: 157-167.
- Poole SK, Patel S, Dehring K, Workman H, Poole CF (2004) Determination of acid dissociation constants by capillary electrophoresis. J Chromatogr A 1037: 445-454.
- Hossain MF, Obi C, Shrestha A, Faruk Khan MO (2014) UV-metric, pH-metric, RP-HPLC methods to evaluate the multiple pKa values of a ployprotic basic novel antimalarial drug lead, cyclen bisquinoline. Modern Chemistry Application 2: 145.
- Chaing PC, Hu Y (2009) Simultaneous determination of logD, logP and pKa of Drugs using a Reverse Phase HPLC coupled with a 96-well plate auto injector. Comb Chem High Throughput Screen 12: 250-257.
- Po HN, Senozan NM (2001) The Henderson-Hasselbach Equation: its History and Limitations. Journal of Chemical Education 78: 1499-1503.
Citation: Vidaud L, Pradines A, Marini J, Lajous E, Clavières P (2016) pKa Determination of a Non-hydro-soluble Chemical Substance, Issued from Chiral Chromatographic Solubility Profiles and Mat-pKa Calculations. J Anal Bioanal Tech 7:299. DOI: 10.4172/2155-9872.1000299
Copyright: © 2016 Vidaud L, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Share This Article
Open Access Journals
Article Tools
Article Usage
- Total views: 15293
- [From(publication date): 4-2016 - Apr 03, 2025]
- Breakdown by view type
- HTML page views: 14355
- PDF downloads: 938