Optimal Energy Control of Double-Stator Induction Motor Regime Using Particle Swarm Optimization
Received: 10-Feb-2020 / Manuscript No. IEP-24-128676 / Editor assigned: 13-Feb-2020 / PreQC No. IEP-24-128676 (PQ) / Reviewed: 27-Feb-2020 / QC No. IEP-24-128676 / Revised: 15-Mar-2024 / Manuscript No. IEP-24-128676 (R) / Published Date: 12-Apr-2024 QI No. / IEP-24-128676
Abstract
In this paper a problem of energy optimization of a Double Stator Induction Motor (DSIM) is considered. Using the concept of a Rotor Field Oriented Control (RFOC); the DSIM Blondel-Park model is used as dynamic constraints in an optimal control problem. A cost function consists of linear combination of magnetic energy, copper losses and mechanical power is minimized. From the Particle Swarm Optimization (PSO) algorithm, a time-varying expression of a minimum-energy rotor flux is obtained. Compared to the constant rotor flux approach, it is proved that higher performances are achieved. The simulation results show the satisfactory behavior of the proposed identification algorithm.
Keywords
Double-stator induction machine; Field-oriented control; Particle swarm optimization; Optimal control; Energy minimization
Introduction
The absolute biggest chances to save energy and diminish working costs in structures and modern offices come from advancing electric engine frameworks. As a general rule, the most piece of power expected moves through engines principally enlistment engines. The DSIM is the prevailing innovation utilized today because of its superior presentation, its high dependability and its speed and force abilities. The regular RFOC technique working at steady rotor motion standard fixed at its standard level gives maximal effectiveness when the framework works at its standard working point. A long way from this, the machine's proficiency diminishes; it can result from a force greatness change. In this way different methods of motion activity are expected to arrive at framework with ideal exhibitions [1].
In numerous applications, effectiveness enhancement of DSIM presents a significant component of control particularly for independent electrical footing. The extremely broad utilization of DSIM suggests that in the event that misfortunes in DSIM drives can be decreased by only a couple of percent, it will significantly affect the all out electrical energy utilization. In high powerful exhibitions control like field-arranged control and direct force control, the motion is normally kept up with steady equivalent to its ostensible worth [2-4]. In this present circumstance the enlistment engine run effectively around the ostensible point. At the point when the heap is decreased extensively, the effectiveness is likewise significantly diminished.
Numerous scientists have been accounted for a few systems utilizing various factors to limit misfortunes in the machine. Among these works, the people who were keen on meta-heuristic methodologies [5-9]. In this specific circumstance, I.Ya. Braslavsky, et al. proposed a hereditary calculation to find the negligible misfortune motion direction [10]. They were keen on incessant beginning electrical drives. Ahmad Moghadam and Ali Reza Seifi offer another way to deal with the issue of Ideal Receptive Power Control Factors arranging (ORPVCP) of an enlistment engine [11]. The fundamental thought is division of Burden Length Bend (LDC) into a few time stretches with steady dynamic power interest in every span and afterward tackling the Energy Misfortune Minimization (ELM) issue.
They acquire an ideal introductory arrangement of control factors of the framework so that is substantial forever stretches and can be utilized as an underlying working state of the framework. In this paper, the ELM issue has been addressed by the Straight Programming (LP) and the Fluffy Direct Programming (Fluffy LP) and developmental calculations. The outcomes are contrasted and the proposed Fluffy TLBO strategy.
In the creators present a methodology for proficiency enhancement of a vector controlled enlistment engine drive [12]. The ideal motion delivering current is acquired utilizing a fake brain organization. The counterfeit brain network model is laid out utilizing Matlab/Simulink and in light of the heap force and speed information of a backhanded vector-controlled acceptance engine drive [13]. The difference in iron center misfortune opposition because of motion and recurrence variety is thought about [14]. Reenactment consequences of the proposed approach show a critical improvement in energy saving and productivity enhancement. Similarly, in the creators present a definition of a sequencing issue with the double objectives of changing the parts usage at various workstations of the sequential construction system and shifting the responsibility related with every workstation [15]. This paper presents a Discrete Molecule Multitude Streamlining (DPSO) calculation, a Memetic calculation (Mama), a Weighted aggregate Multi-Objective Hereditary Calculation (MOGAW) and a Non-ruled Arranging Hereditary Calculation (NSGA-II) to settle an in the nick of time sequencing issue where these targets are to be improved all the while. Exploratory outcomes show that discrete molecule multitude streamlining beats different calculations in regard of an examination metric.
Liu X, et al. take care of an ideal control issue for a class of timeinvariant exchanged stochastic frameworks with multi-exchanging times, where the goal is to limit an expense utilitarian with various costs characterized on the states [16]. In light of the math of variety, the creators determine the slope of the expense utilitarian as for the turning times on a particularly basic structure, which can be straightforwardly utilized in inclination drop calculations to find the ideal exchanging moments.
Notwithstanding these investigations, this paper gives a Molecule Multitude Improvement (PSO) commitment. The proposed approach is utilized as improvement looking through calculation because of its benefits over different methods for lessening the levelized cost of energy. PSO calculation utilizes as "populace" the directions of the reference rotor transition. The issue is characterized and objective capability is presented taking in thought wellness values awareness in molecule swarm process. The prevalence of the proposed approach has been shown by contrasting the outcomes and the regular RFOC technique [17].
The body of this paper is coordinated as follows: Area 2 is primarily expected to portray the full DSIM model. Segment 3 is committed to introduce the energy-power cost capability. We grow in segment 4, the PSO approach and we present a reproduction results contrasting and the regular RFOC. Area 5 finishes up the paper.
Materials and Methods
Double-star induction motor model
The DSIM is built with two symmetrical three-phase armature winding systems, electrically displaced by 30°. Its rotor has a conventional structure. Figure 1 shows the position of the natural frame relative to the common reference frame.
The full-order model of the DSIM viewed from the synchronous rotating reference frame is given by the following system.
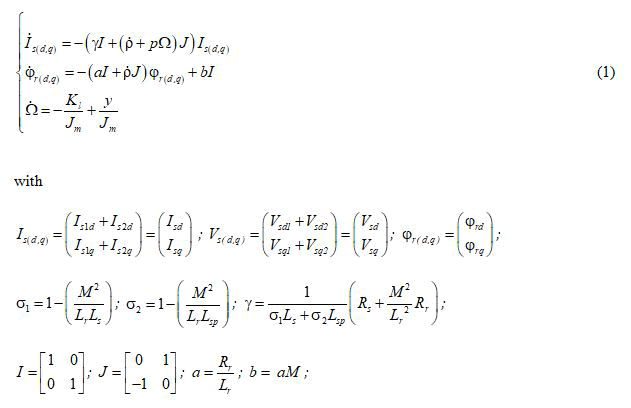
By noting ωs=ρ is the sleep frequency, Rs and Rr are stator and rotor resistances, Ls and Lr are stator and rotor inductances; M is the magnetizing inductance, Lsp is the principal cyclic inductance. Jm is the total moment of inertia of the rotor, Ki is the load torque constant. Isd1, Isd2, Isq1 and Isq2 are respectively the direct and quadrature current of stator 1 and stator 2. Vsd1, Vsd2, Vsq1, Vsq2 are respectively, the stator voltages in d-q axis of each stator, p is the poles number, Y is the electromagnetic torque expressed as follows:
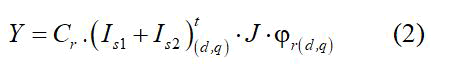
Generally speaking, the control law strategy aims to force the system to satisfy specified closed-loop differential equations. Here, the stator current is taken as an input control of the system. A high gain control current loop is chosen in order to simplify the optimization algorithm [18]. Such choice permits to apply a reduced order current fed DSIM model; the current loop is given [19].
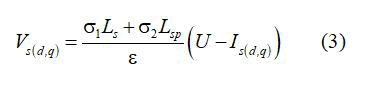
and a reduced model of the DSIM is built as follows:
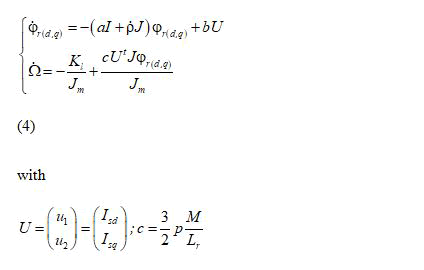
Results and Discussion
Energy model of a double-star induction motor
The instantaneous active power in the d-q rotating frame is given by:

The relation between stator and rotor currents can be given as follows:

From equations (1) and (6), the input power is given by:

Finally, the instantaneous active power can be defined as the following sum:

By means of a field-oriented control drive:
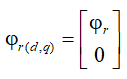
The derivate of stored magnetic can be expressed as follows:
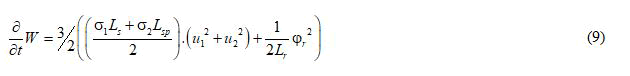
We define also the total copper losses as:
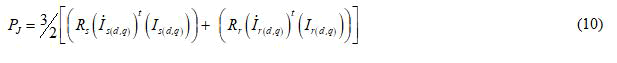
By using equations (1) and (6), those losses can be expressed with respect to U and φr as follows:
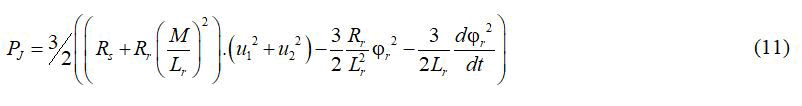
The mechanical power of the DSIM is given as follows:

In term of rotor variables and torque current, we get:

An optimal control consists on minimization of a cost function. In this case, the cost function can be defined as the integral of an index f (Isd, Isq, φr, Ω) given as follows:

The index corresponds to the weighted sum:

The weighting factors (α1, α2, α3) are used to scale power-energy combined convex criteria terms defined above.
Using equations (4), (6), (7) and (9), the cost function is given as follows:
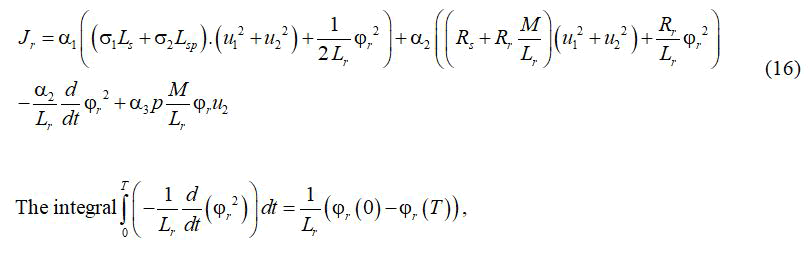
Has no effect in the optimizing problem and can be omitted it from the integral. Considering the new control vector.
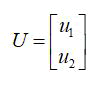
The system described by (2) can be defined as follows:

Find the optimal control variables (u1*) and (u2*) that minimize the following cost function:
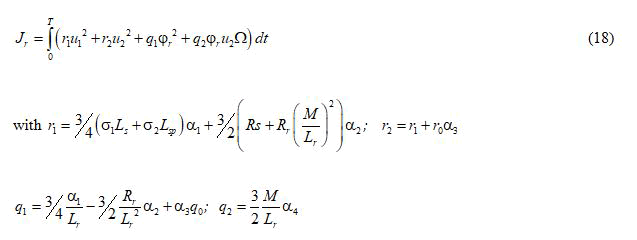
Where the weighting factors r1, r2, q1 and q2 must be positives.
Energy optimization via PSO algorithm
PSO calculation is a populace based streamlining strategy motivated by the movement of a bird rush, or fish tutoring. Such gatherings are social associations whose general conduct depends on a correspondence among individuals from some kind or another and participation. All individuals comply with a bunch of basic principles that model the correspondence inside the group and between the herd and the climate [20]. The worldwide way of behaving, in any case, is undeniably more perplexing and for the most part effective. For example, a group is generally effective at finding the best spot for taking care of, same which appears to be difficult to accomplish by any single part [21].
An individual from the group is classified "molecule", in this way a herd is an assortment of particles. The well known term "flying the particles" signifies the investigation of the pursuit space. Each molecule knows its ongoing position and the best position visited starting from the primary fly [22]. PSO performs investigation by ceaselessly detecting (perusing) the hunt space at neighborhood level. The data gathered by the particles is focused and arranged to track down the best part (called worldwide best). The new best part and the ongoing best part are thought about and the best one is kept as worldwide best. Its position is conveyed to all run individuals in this way in the following fly the particles know where the best spot lies in the pursuit space. Finding the following best spot is the principal errand of the group for which investigation and in this way populace variety is significant. In this situation the group investigates the space however stays stable in the wake of shifting its flying course (fourth standard). Simultaneously, in any case, all rush individuals are drawn in by the place of the worldwide best (Figure 2).
The two fundamental conditions which administer the working of PSO are that of speed vector and position vector are given by:
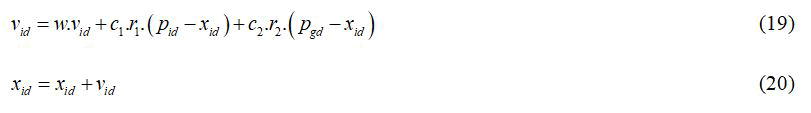
Acceleration constants c1, c2 and inertia weight are the predefined by the user and r1, r2 are the uniformly generated random numbers in the range of (0, 1).
The objective of optimization problem is to look for the values of the variables being optimized, which satisfy the defined constraints and maximize or minimize the fitness function. In this work consumption energy defined in equation (18) is used as fitness function.
Then, PSO is used to find the optimal rotor flux φr from the energy model of DSIM under variable load and speed. The flux φr* is defined as a third order polynomial that depends on time t such as:

A concept consists on researching parameters p0, p1, p2 and p3, in bounded intervals previously defined, which enable reconstructing the optimal value of the rotor flux.
The simulations results are carried out on a three-phase DSIM, 380 V, 20 KW, 50 Hz and 4 poles, squirrel cage induction motor. The motor parameters are Rs=0.4 Ω, Rr=0.096 Ω, Lr=8.9 mH and Ls=81.2 mH. The mechanical parameter are Jm=0.6 and Ki=0.7. The load torque is assumed to be proportional to the reference speed with Kt=0.7 is the constant of proportionality. Study is carried out over a period of 2 seconds. The other parameters set in PSO algorithm are given in the Table 1.
| Swarm size | 30 |
| Iterations | 20 |
| c1 | 1.5 |
| c2 | 1.5 |
| w1 (Inertia weight at the start of PSO run) | 0.4 |
| w2 (Inertia weight at the end of PSO run) | 0.9 |
Table 1: Strategy parameters for identification of PSO model.
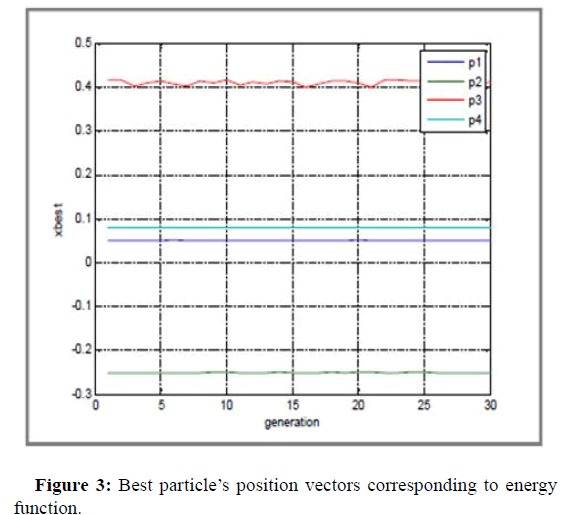
The best particle’s position vectors corresponding to our cost function are represented by Figure 3.
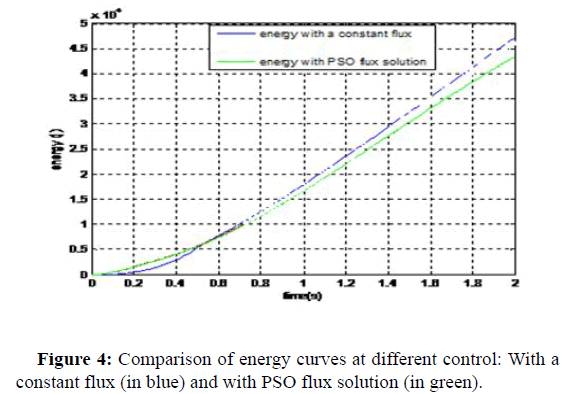
Figure 4 show the evolution of the absorbed energy. We can observe a decreasing of absorbed energy values given by PSO flux solution compared with the classic RFOC.
Table 2 presents the gain in energy of each method compared to the classic RFOC.
| Energy using CST flux (j)=44777 | ||
|---|---|---|
| Simulation | Energy using PSO (j) | Minimization via PSO (%) |
| 1 | 42847 | -4.31 |
| 2 | 42116 | -5.94 |
| 3 | 42314 | -5.5 |
| 4 | 42351 | -5.41 |
| 5 | 42557 | -4.95 |
| 6 | 41836 | -6.56 |
| 7 | 42692 | -4.65 |
| 8 | 42368 | -5.38 |
| 9 | 42638 | -4.77 |
| 10 | 42652 | -4.74 |
| Average | 42437.1 | -5.221 |
Table 2: Results of PSO optimization for different generation.
The proposed fuzzy PSO optimization procedure has compared to a conventional vector control operating at rated rotor flux. These obtained results are then introduced in a lookup table and finally inserted in the control block. The energy minimization is greatly improved over a region wide range when using this method compared with the conventional method. The PSO results are greatly improved particularly over the light load region through which habitually the optimization values are relatively low.
Conclusion
An energy enhancement technique for a twofold stator enlistment engine control utilizing molecule multitude improvement is introduced in this paper. This technique comprises to find the ideal rotor motion. The connection between ideal rotor transition and engine misfortune minimization in the enlistment engine vector control framework is researched. It is pointed that the engine energy minimization can be accomplished by limiting all out misfortunes by and by. Recreation results were explored with a consistent transition activity and ideal motion utilizing molecule multitude improvement. PSO-based approach permitted a lot of lower energy utilization and an improved effectiveness than different techniques.
References
- Mimouni MF, Dhifaoui R (2002) Modelling and simulation of a double‐star induction machine vector control using copper‐losses minimization and parameters estimation. Int J Adapt Control Signal Process 16: 653-680.
- Mimouni MF, Dhifaoui R (2004) A robust air‐gap flux estimation for speed sensorless vector control of double‐star induction machine. Int J Adapt Control Signal Process 18: 523-546.
- Khedher A, Mimouni MF (2010) Sensorless-adaptive DTC of double star induction motor. Energy Convers Manag 51: 2878-2892.
- Arias A, Romeral L, Aldabas E, Jayne M (2005) Stator flux optimised direct torque control system for induction motors. Electr Power Syst Res 73: 257-265.
- Lorenz RD, Yang SM (1992) Efficiency-optimized flux trajectories for closed-cycle operation of field-orientation induction machine drives. IEEE Trans Ind Appl 28: 574-580.
- de Wit CC, Ramirez J (1999) Optimal torque control for current-fed induction motors. IEEE Trans Autom Control 44: 1084-1089.
- Medagam P, Pourboghrat F (2007) Online H∞ speed control of sensorless induction motors with rotor resistance estimation. 7th International Conference of the IEEE Power Electronics and Drive Systems, Bangkok, pp. 1307-1312.
- Munteanu Tr, Rosu E, Gaiceanu M, Paduraru R, Dumitriu T, et al. (2009) The optimal control for position drive system with induction machine. 13th European Conference of the IEEE Power Electronics and Applications, Barcelona, pp. 1-8.
- Wang A, Ling Z (2009) Improved efficiency optimization for vector controlled induction motor. IEEE Power and Energy Engineering Conference, Wuhan, pp. 1-4.
- Braslavsky I, Ishhmatov Z, Plotnikov Y, Averbakh I (2006) Energy consumption and losses calculation approach for different classes of induction motor drives. International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Taormina, pp. 1449-1452.
- Moghadam A, Seifi AR (2014) Fuzzy-TLBO optimal reactive power control variables planning for energy loss minimization. Energy Convers Manag 77: 208-215.
- Abdin ES, Ghoneem GA, Diab HMM, Deraz SA (2003) Efficiency optimization of a vector controlled induction motor drive using an artificial neural network. Industrial Electronics Society, The 29th Annual Conference of the IEEE, United States, pp. 2549-2548.
- Hamid RHA, Amin AMA, Ahmed AMA, El-Gammal AAA (2006) Optimal operation of induction motors using artificial neural network based on Particle Swarm Optimization (PSO). Industrial Technology, IEEE International Conference, Mumbai, pp. 2408-2413.
- Kim DH, Hirota K (2008) Vector control for loss minimization of induction motor using GA-PSO. Appl Soft Comput 8: 1692-1702.
- Alaghebandha M, Hajipour V, Hemmati M (2017) Optimizing multi-objective sequencing problem in mixed-model assembly line on just-in-time: Particle swarm optimization algorithm. Int J Manag Sci Eng Manag 12: 288-298.
- Liu X, Li S, Zhang K (2017) Optimal control of switching time in switched stochastic systems with multi-switching times and different costs. Int J Control 90: 1604-1611.
- Liu X, Zhang K, Li S, Fei S, Wei H (2015) Optimal control of switching times in switched stochastic systems. Asian J Control 17: 1580-1589.
- Abdelati R, Mimouni MF (2010) Minimum energy consumption of an induction motor in dynamic regime. J Electr Eng 10: 91-101.
- Ramirez JM (1998) Contribution to the optimal control of asynchronous machines. Automatic Laboratory of Grenoble, France.
- Abdelati R, Mimouni MF (2011) Analytical solution of optimized energy consumption of induction motor operating in transient regime. Eur J Control 17: 397-411.
- Eberhart RC, Shi Y (2000) Comparing inertia weights and constriction factors in particle swarm optimization. IEEE Publishers, United States, pp. 84-88.
- Tchomte SK, Gourgand M (2009) Particle swarm optimization: A study of particle displacement for solving continuous and combinatorial optimization problems. Int J Prod Econ 121: 57-67.
Citation: Kortas I, Sakly A, Mimouni MF (2024) Optimal Energy Control of Double-Stator Induction Motor Regime Using Particle Swarm Optimization. Innov Ener Res 13: 383.
Copyright: © 2024 Kortas I, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Share This Article
Recommended Journals
Open Access Journals
Article Usage
- Total views: 680
- [From(publication date): 0-2024 - Mar 29, 2025]
- Breakdown by view type
- HTML page views: 496
- PDF downloads: 184