Optimal Energy Control of Double-Star Induction Motor in Transient regime using Analytic solution and Particle Swarm Optimization
Received: 08-Mar-2024 / Manuscript No. iep-24-130220 / Editor assigned: 10-Mar-2024 / PreQC No. iep-24-130220 (PQ) / Reviewed: 23-Mar-2024 / QC No. iep-24-130220 / Revised: 30-Mar-2024 / Manuscript No. iep-24-130220 (R) / Accepted Date: 30-Mar-2024 / Published Date: 01-Apr-2024 QI No. / iep-24-130220
Abstract
This paper investigates the importance of controller’s energy optimization opportunity of a Double-Star Induction Motor (DSIM). We introduce a concept of a nonlinear functions minimization using tow topologies namely energy model based optimal flux using Euler equation and a minimum energy consumption using particle swarm methodology (PSO). In this study, the rotor flux level in a machine has been considered to be adjusted to give minimum energy for a given load of the motor in dynamic regime. Good results are obtained with PSO in dynamic regime, compared to Euler equation based on analytic solution.
Keywords
Double-Star Induction Machine; Field-Oriented Control; Particle Swarm Optimization; Optimal control; Energy minimization; Transient regime; Euler equation.
Introduction
Electrical machines consume most of the world’s electrical energy every year. Improving efficiency of electrical drives is important not only for energy saving, but also for environmental protection. In an induction motor drive system, to get a best transient response the induction motor normally operates at rated flux. However, when the drive system operates with light loads, the core losses become excessive, causing drive system poor efficiency. To improve the motor efficiency, the flux must be decreased, obtaining a balance between the copper and iron losses.
The double-star machines become more attractive in industrial applications. Nevertheless, this concept is not really recent but has been introduced since the beginning of the last century. The Double- Star Induction Motor (DSIM) has two systems in the stator windings of three phase shifted them to an electrical angle (in this model we take ). Both three-phase winding systems are supplied with the same frequency and the rotor is a classical squirrel cage. Due to its high performance, its high reliability, and its speed and torque capabilities, there are several works on the vector control of the DSIM [1].
In many applications, efficiency optimization of DSIM presents an important factor of control especially for autonomous electrical traction. The very extensive use of DSIM implies that if losses in DSIM drives can be reduced by just a few percent, it will have a major impact on the total electrical energy consumption. In high dynamic performances control schemes used in industrial applications like Field-Oriented Control [2] and Direct Torque Control [3], the flux is usually maintained constant equal to its nominal value; in this situation the induction motor run efficiently around the nominal point. When the load is reduced considerably, the efficiency is also greatly reduced. Many researchers have been reported several strategies using different variables to minimize losses in the machine. Among these works, those who were interested in the variational calculus: Robert D.
Lorenz et al. [4], have opted for an operating loss modelled by copper and iron losses. In order to compute the minimal loss flux trajectory, they developed an optimal control strategy using a dynamic programming technique. C. Canudas de Wit et al. [5] considered a convex energy cost function including the stored magnetic energy and coil losses. They developed a nonlinear Euler-Lagrange equation from which an optimal flux norm trajectory can be derived. The obtained equation was unsolvable for an arbitrary torque. They proposed a suboptimal analytical solution aligned with a constant torque operation. Like C. Canudas de Wit et al. [5], Peda V. Medagam et al. [6] have proposed an online technique for the control based on the optimal control theory. The authors in [5] have used measured errors of flux and stator currents as new state variables in the optimal control problem. But Medagam et al. [6] considered the integral of the speed and the flux norm tracking errors as the new state variables. Tr. Munteanu et al. [7] used the Riccati differential matrix equation to solve a quadratic performance criterion that involves energy in both inertia and motor windings. They gave an online numerical solution for the IM drive. Aiyuan Wang et al. [8] proposed a performance criteria index containing copper and iron losses.
In others studies, a new control strategy uses meta-heuristic is proposed. Indeed, the appearance of evolutionary algorithms had the effect of a bomb in the fields of complex problem solving, especially in the optimization function with constraints. In this context, I.Ya. Braslavsky et al. [9] proposed a genetic algorithm to find the minimal loss flux trajectory. They were interested in frequent-starting electrical drives. Ahmad Moghadam and Ali Reza Seifi [10] offer a new approach to the problem of Optimal Reactive Power Control Variables planning (ORPVCP) of an IM. The basic idea is division of Load Duration Curve (LDC) into several time intervals with constant active power demand in each interval and then solving the Energy Loss Minimization (ELM) problem to obtain an optimal initial set of control variables of the system so that is valid for all time intervals and can be used as an initial operating condition of the system. In this paper, the ELM problem has been solved by the Linear Programming (LP) and the Fuzzy Linear Programming (Fuzzy-LP), and evolutionary algorithms i.e. MHBMO and TLBO. The results are compared with the proposed Fuzzy-TLBO method. The authors in [11] present an approach for efficiency optimization of a vector-controlled induction motor drive. The optimum flux-producing current is obtained using an artificial neural network. The artificial neural network model is established using Matlab/Simulink and based on the load torque and speed data of an indirect vector-controlled induction motor drive. The change of iron core loss resistance due to flux and frequency variation is taken into consideration. Simulation results of the proposed approach show a significant improvement in energy saving and efficiency optimization. In the same way,
Hamid R.H.A et al. [12] present the application of neural network based on PSO for losses and operating cost minimization control in the induction motor drives. In this paper, four strategies for induction motor speed control are proposed. Those four strategies are based on PSO and called maximum efficiency strategy, minimum stator current strategy, maximum power factor strategy, and maximum weighted cost strategy. The proposed technique is based on the principle that the flux level in a machine can be adjusted to give the minimum amount of losses and minimum operating cost for a given value of speed and load torque. The main advantages of the proposed technique are; its simple structure and its straightforward maximization of induction motor efficiency and its operating cost for a given load torque.
In [13], a vector control approach is suggested for an optimal operation of induction motor using variable acceleration and GA–PSO tuning method through simulation. Satisfactory results for energy saving control are obtained.
In addition to these studies, this paper provides two contributions: Analytic optimal control strategy: a cost-to-go function can be minimized and subjected to the motor dynamic equations and boundary constraints in order to find rotor flux optimal trajectories. This cost-togo function consists of a linear combination of magnetic power, copper loss, and mechanical power. The Dynamic equations are represented by using a reduced Blondel Park model of induction motor. From the Euler-Lagrange equation, a system of nonlinear differential equations is obtained, and analytical solutions of these equations are achieved so as to obtain a time-varying expression of a minimum-energy rotor flux. Under Rotor Field-Oriented Control (RFOC), this analytical solution of rotor flux achieved maximum DSIM’s efficiency and was implemented in transient torque. Particle Swarm Optimization (PSO): The proposed approach is used as optimization searching algorithm due to its advantages over the other techniques for reducing the Levelized cost of energy. PSO algorithm uses as "population" the coordinates of the reference rotor flux. The problem is defined and objective function is introduced taking in consideration fitness values sensitivity in particle swarm process. The superiority of the proposed approach has been shown by comparing the results with analytic solution.
In order to prove the validity and the effectiveness of these proposed optimal control strategies using minimum-energy rotor flux trajectory, we conclude with the simulation results by comparing theses methods with the conventional RFOC.
The body of this paper is organized as follows: section 2 is mainly intended to describe the full DSIM model. Section 3 is devoted to present the reduced model. In the fourth section the energy model of the DSIM is explained, minimum energy approaches are presented in details by the energy-power cost function. The deadbeat rotor flux controller and the RFOC scheme are presented in section 5. Section 6 deals with the simulation results by comparing the two optimized RFOC. Section 7 concludes the paper.
Double-star induction motor model
The DSIM is built with two symmetrical three-phase armature winding systems, electrically displaced by 30°. Its rotor has a conventional structure. Figure 1 shows the position of the natural frame relative to the common reference frame.
In a reference frame rotating to the synchronous speed, equations defining the full-order dynamic model of the double star asynchronous machine are given by the system (1): [1]
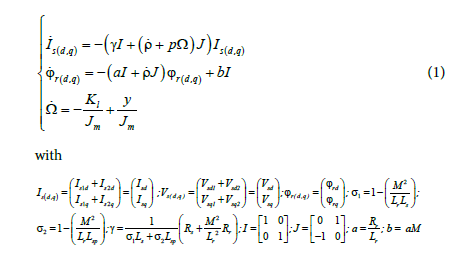
By noting ω = ρ s is the sleep frequency, Rs and Rr are stator and rotor resistances, Ls and Lr are stator and rotor inductances; M is the magnetizing inductance, Lsp is the principal cyclic inductance. Jm is the total moment of inertia of the rotor, Kl is the load torque constant. Isd1, Isd2, Isq1 and Isq1 are respectively the direct and quadrature current of stator 1 and stator 2. Vsd1, Vsd2, Vsq1, Vsq2 are respectively, the stator voltages in d-q axis of each stator, p is the poles number, Y is the electromagnetic torque expressed as follows:
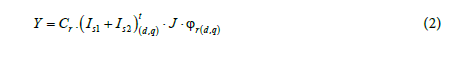
Generally speaking, the control law strategy aims to force the system to satisfy specified closed-loop differential equations. Here, the stator current is taken as an input control of the system. A high gain control current loop is chosen in order to simplify the optimization algorithm [14]. Such choice permits to apply a reduced order current fed DSIM model; the current loop is given by [15]:
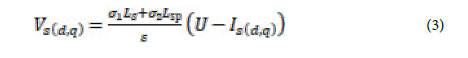
and a reduced model of the DSIM is built as follows:
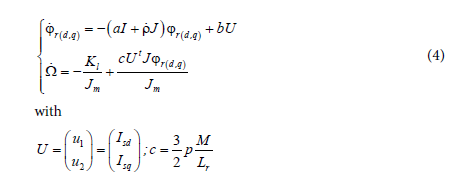
Energy model of a double-star induction motor
The instantaneous active power in the d-q rotating frame is given by:

The relation between stator and rotor currents can be given as follows:

From equations (1) and (6), the input power is given by:
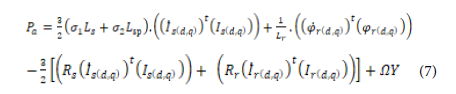
Finally, the instantaneous active power can be defined as the following sum: [1]

By means of a field-oriented control drive: 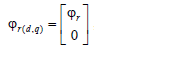 the
derivate of stored magnetic given in (8) can be expressed from (7) as
follows:
the
derivate of stored magnetic given in (8) can be expressed from (7) as
follows:
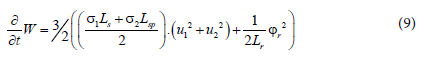
We define also the total copper losses as:
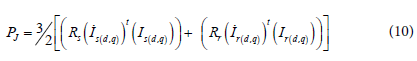
By using equations (1) and (6), those losses can be expressed with respect to and as follows:
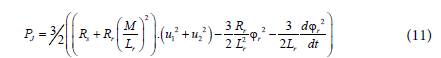
The mechanical power of the DSIM is given as follows:

In term of rotor variables and torque current ( Isq ) , we get:

An optimal control consists on minimization of a cost function. In this case, the cost function can be defined as the integral of an index (Isd,Isq,ϕr,Ω )given as follows:

The index corresponds to the weighted sum:
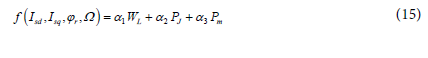
The weighting factors (α1, α2,α3) are used to scale power-energy combined convex criteria terms defined above.
Development of optimal strategies control of a double star induction motor
Energy minimization using Euler equation
Minimize the cost function provides two important advantages: first, minimizing the corresponding magnetic energy stored, allowing thus the maximization of the power factor, the second being the minimization of losses in the windings thus increasing the machine efficiency.
Using equations (4), (6), (7) and (9), the cost function is given as follows:
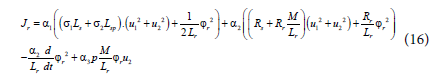
The integral 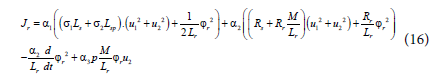 has no effect in the optimizing problem and can be omitted it from the integral.
has no effect in the optimizing problem and can be omitted it from the integral.
Considering the new control vector  , the system described
by (2) can be defined as follows:
, the system described
by (2) can be defined as follows:

Find the optimal control variables (u1*) and (u2*) that minimize the following cost function:
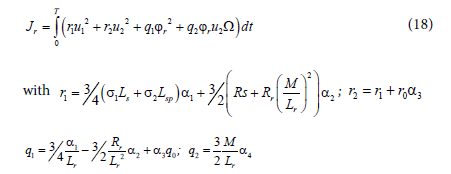
where the weighting factors r1, r2, q1 and q2 must be positives.
The optimal control problem amounts to determine the optimized values of u1* and u2* which are defined as follows:

By injecting the expressions of u1 and u2 from the system (19) in the cost function in (18) we get:
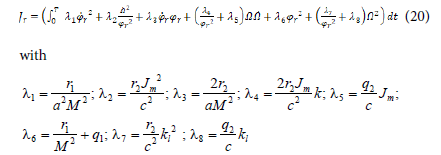
must be positive constants defined accordingly to the condition on the constants r1, r2, q1and q2.
This integral given by (20) can be expressed as follows:

and can be solved using Euler-Lagrange equation [16,17], with respect to the following condition: This integral has a minimum value ϕr* and Ω* if their trajectory satisfies the following conditions:
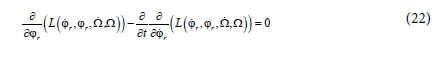
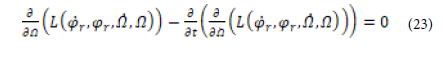
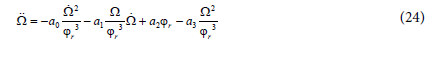
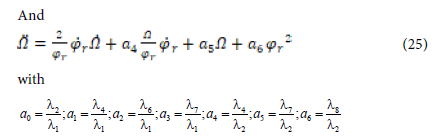
In order to obtain an accelerate mode (transient regime), we have proposed a linear law for the motor speed as follows:

Hence, the second Equation (25) has no physical meaning and can be skipped. By substituting the expression of Ω by Ω* given in (26), equation (24) becomes:
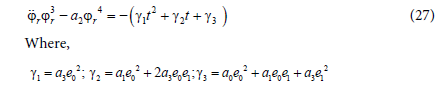
Despite the extreme difficulty to solve this equation (27), we tried
to find a solution using a mathematical calculation. So, we applied the
method of integration by parts to this equation, during a time interval
[0,t].
By integrating (27), we obtain a first order differential equation:
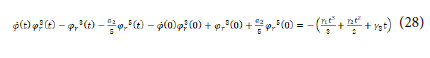
If we make a second integration, we have:
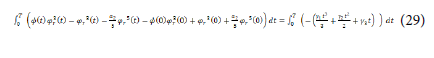
This implies:
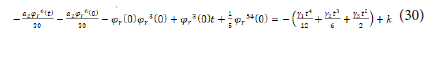
Where, k is an appropriate positive constant.
This yield:
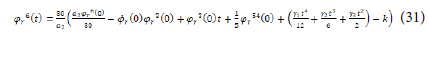
Finally, the optimal solution of the rotor flux is given by the following expression:
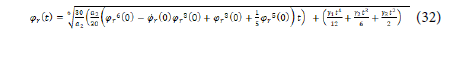
Energy optimization via PSO algorithm
Many recent developments in science demand numerical techniques for searching global optima to corresponding optimization problems [18]. PSO technique is a population based stochastic search technique first introduced by Kennedy and Eberhart [19,20]. PSO algorithm is a population-based optimization technique inspired by the motion of a bird flock, or fish schooling. Such groups are social organizations whose overall behavior relies on some sort of communication amongst members, and cooperation. All members obey a set of simple rules that model the communication inside the flock, and between the flock and the environment. The global behavior, however, is far more complex and generally successful. For instance, a flock is usually successful at finding the best place for feeding, same which seems impossible to achieve by any single member.
A member of the flock is called “particle”; thus, a flock is a collection of particles. The popular term “flying the particles” means the exploration of the search space. Every particle knows its current position and the best position visited since the first fly. PSO performs exploration by continually sensing (reading) the search space at local level. The information collected by the particles is concentrated and sorted to find the best member (called global best). The new best member and the current best member are compared and the best one is kept as global best. Its position is communicated to all flock members thus in the next fly the particles know where the best spot lies in the search space. Locating the next best spot is the main task of the flock for which exploration and therefore population diversity is crucial. In this scenario the flock explores the space but remains stable after changing its flying direction (fourth principle). At the same time, however, all flock members are attracted by the position of the global best.
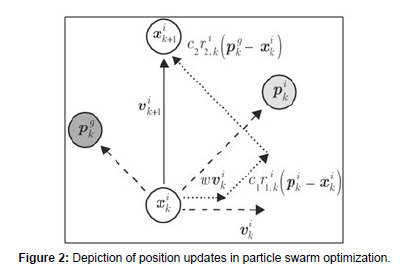
The two basic equations which govern the working of PSO are that of velocity vector ( vid) and position vector (xid ) are given by [21]:
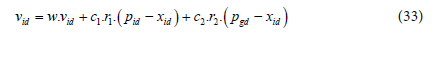

Figure 2 shows the depiction of position updates in particle swarm optimization. Acceleration constants c1, c2 and inertia weight w are the predefined by the user and r1, r2 are the uniformly generated random numbers in the range (Figure 2) [1].
The objective of optimization problem is to look for the values of the variables being optimized, which satisfy the defined constraints and maximize or minimize the fitness function. In this work consumption energy defined in equation (18) is used as fitness function.
Then, PSO is used to find the optimal rotor flux r ϕ from the energy model of DSIM under variable load and speed. The flux * r ϕ is defined as a third order polynomial that depends on time t such as:
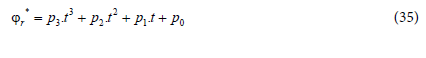
A concept consists on researching parameters p0, p1, p2 and p3, in bounded intervals previously defined, which enable reconstructing the optimal value of the rotor flux.
Table 1 presents chosen parameters for identification of PSO algorithm.
| Swarm Size | 30 |
| Iterations | 20 |
| C1 | 1.5 |
| C2 | 1.5 |
| W1 (Inertia weight at the start of PSO run) | 0.4 |
| W2 (Inertia weight at the end of PSO run) | 0.9 |
Table 1: Strategy parameters for Identification of PSO model.
Deadbeat Control of the Rotor Flux Level
These kinds of problems need wide range of the rotor flux magnitude variation. A deadbeat response has been chosen to regulate the rotor flux level [14]. In this part, the mutual inductance value of the machine under this consideration is not used. In a rotation reference frame, the rotor flux can be expressed using the proposed control approach as follows:

the variation of the mutual M can be given by:
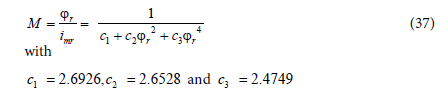
imr is the magnetizing rotor current.
The reference value of current Isd*can be written as:
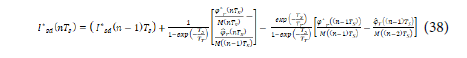
where (Ts) is the setting time, (Tr) is the rotor time constant, ϕrˆ(iTs ) and M(iTs) are respectively the estimated rotor flux and the mutual inductance at sampling (iTs).
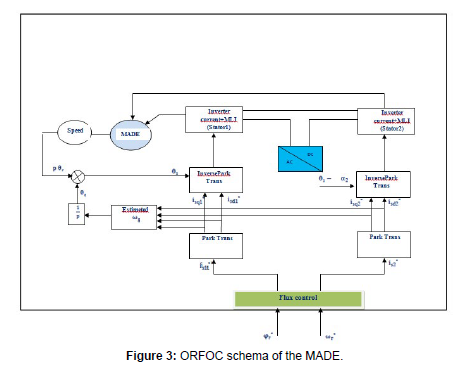
The ORFOC of the DSIM is given by Figure 3:
Simulations Results
The simulations results are carried out on a three-phase DSIM, 380V, 20KW, 50Hz and 4 poles, squirrel cage induction motor. The motor parameters are:
Rs = 0.4Ω , Rr = 0.096Ω , Lr = 8.9mH and Ls = 81.2mH . The mechanical parameter is Jm= 0.6 and Kl= 0.7 .
The load torque is assumed to be proportional to the reference speed with Kl= 0.7 is the constant of proportionality. Study is carried out over a period of 2 seconds.
The Proposed fuzzy PSO optimization procedure has compared to both a conventional vector control operating at rated rotor flux and optimal control using Euler equation. These obtained results are then introduced in a lookup table and finally inserted in the control block. Figure 4 presents the convergence graph of energy function for 20 generation.
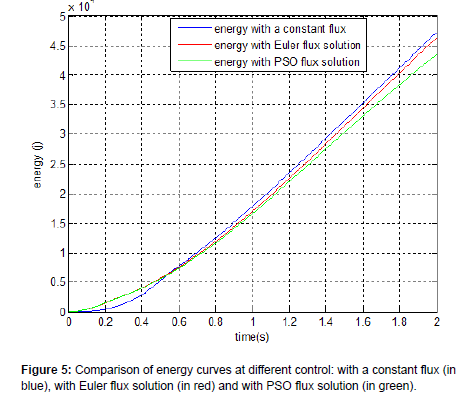
The energy minimization is greatly improved over a region wide range when using this method compared with other methods as showed in Figure 5. The PSO results are greatly improved particularly over the light load region through which habitually the optimization values are relatively low.
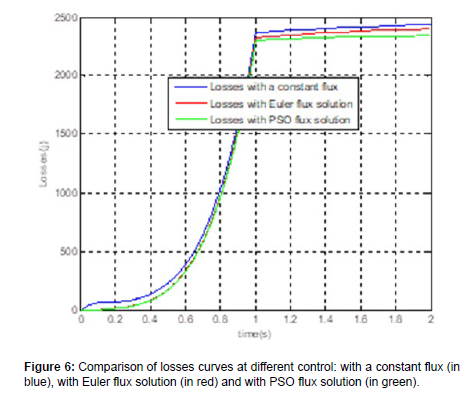
It is obvious to remark from Figure 6 a significant decrease of losses compared to the one delivered by the conventional RFOC and Euler solution. This means that the presented method saves energy.
Table 2 presents the gain in energy of each method compared to the classic RFOC.
Energy using CST flux (j) |
44 777 | ||
|---|---|---|---|
| Energy using Euler equation (j) | 44 322 | ||
| (-1.01%) | |||
| Iterations | Energy using PSO | Minimization via PSO (%) | |
| (j) | |||
| g1 | 42 847 | -4.31 | |
| g2 | 42 116 | -5.94 | |
| g3 | 42 314 | -5.5 | |
| g4 | 42 351 | -5.41 | |
| g5 | 42 557 | -4.95 | |
| g6 | 41 836 | -6.56 | |
| g7 | 42 692 | -4.65 | |
| g8 | 42 368 | -5.38 | |
| g9 | 42 638 | -4.77 | |
| g10 | 42 652 | -4.74 | |
| average | 42 437.1 | -5.221 | |
Table 2: Results of PSO optimization generations
Conclusion
An energy optimization method for Double Star Induction Motor control using Particle Swarm Optimization is presented in this paper.
This method consists to find the optimal rotor flux. The relationship between optimal rotor flux and motor loss minimization in the induction motor vector control system is investigated. It is pointed that the motor energy minimization can be achieved by minimizing total losses in practice. Simulation results were investigated with three topologies namely constant flux operation, flux solution using Euler equation and optimal flux using Particle Swarm Optimization. PSObased approach allowed much lower energy consumption and a better efficiency than other strategies.
Conflict of Interest
The authors declare that there is no competing financial interest or personal relationship that could have appeared to influence the work reported in this paper
References
- Mimouni MF, Dhifaoui R (2002) Modelling and Simulation of Double-Star Induction Machine Vector Control using Copper Losses Minimization and Parameters Estimation.International Journal of Adaptative Control and Signal Processing.
- Mimouni MF, Dhifaoui R (2004) A robust air-gap flux estimation for speed sensorless vector control of double-star induction machine. International Journal of Adaptive Control and Signal Processing.
- Khedher A, Mohamed FM (2010) Sensorless-adaptive DTC of double star induction motor. Energy Conversion and Management: 2878– 2892.
- Lorenz RD, Yang SM (1988) Efficiency-Optimized flux trajectories for closed cycle operation of field-oriented induction machine drives. IEEE Industry application society Annual Meeting.
- De Wit CC, Ramirez J (1999) Optimal Torque Control for Current-feeded Induction Motors. IEEE Transactions on automaticcontrol.
- Medagam PV, Pourboghrat F (2007) Online H∞ Speed Control of Sensorless Induction Motors with Rotor Resistance Estimation. IEEE Power Electronics and Drive Systems.
- Munteanu T, Rosu E, Gaiceanu M, Paduraru R, Dumitriu T et al. (2009) The optimal control for position drive system with induction machine. IEEE Power Electronics and Applications: 1307- 1312.
- Braslavsky I, Ishmatov Z, Plotnikov Y, Averbakh I (2006) Energy Consumption and Losses Calculation Approach for Different Classes of Induction Motor Drives. International Symposium on Power Electronics, Electrical Drives, Automation and Motion: 1560- 1565.
- Wang A, Ling Z (2009) Improved Efficiency Optimization for Vector Controlled Induction Motor. IEEE Power and Energy Engineering Conference 1- 4.
- Moghadam A, Seifi AR (2014) Fuzzy-TLBO optimal reactive power control variables planning for energy loss minimization. Energy Conversion and Management: 208– 215.
- Abdin ES, Ghoneem GA, Diab HM, Deraz SA (2003) Efficiency optimization of a vector-controlled induction motor drive using an artificial neural network. Industrial Electronics Society.
- Hamid RH, Amin AM, Ahmed RS, El-Gammal AA (2006) Optimal Operation of Induction Motors Using Artificial Neural Network Based on Particle Swarm Optimization (PSO). Industrial Technology IEEE International Conference 2408 – 2413.
- Kim DH, Hirota K (2008) Vector control for loss minimization of induction motor using GA–PSO. Energy Conversion and Management 1692- 1702.
- Abdelati R, Mimouni MF (2010) Minimum-Energy Consumption of an Induction Motor in Dynamic Regime. Journal of Electrical Engineering 91- 101.
- Ramirez J (1998) Contribution à la commande optimale des Machines Asynchrones. Automatic Laboratory of Grenoble.
- Abdelati R, Mimouni MF (2002) Analytical Solutions of Optimized Energy Consumption of Induction Motor Operating in Transient Regime. European Journal of Control: 397– 411.
- Russak IB (2002) Calculus of variations. Department of Mathematics.
- Clerc M, Siarry P (2003) Une nouvelle métaheuristique pour l’optimisation difficile : la méthode des essaims particulaires.
- Eberhart R, Kennedy J (1995) A new Optimizer using particle swarm theory. Six international symposium on micro machine and human science: 39- 43.
- Eberhart RC, Shi Y (2000) Comparing inertia weights and constriction factors in particle swarm optimization. IEEE conference proceedings 84- 88.
- Tchomté SK, Gourgand M (2009) Particle Swarm Optimization: A study of particle displacement for solving continuous and combinatorial optimization problems., International Journal of Production Economics: 57- 67.
Citation: Imen K, Anis A, Mimouni MF (2024) Optimal Energy Control of Double-Star Induction Motor in Transient regime using Analytic solution and Particle SwarmOptimization. Innov Ener Res, 13: 392.
Copyright: © 2024 Imen K, et al. This is an open-access article distributed underthe terms of the Creative Commons Attribution License, which permits unrestricteduse, distribution, and reproduction in any medium, provided the original author andsource are credited.
Share This Article
Recommended Journals
Open Access Journals
Article Usage
- Total views: 1045
- [From(publication date): 0-2024 - Apr 26, 2025]
- Breakdown by view type
- HTML page views: 841
- PDF downloads: 204