On the Thermal Conductivity of Magnets near the Point of Phase Transition
Received: 21-Jul-2021 / Manuscript No. JMSN-22-15953 / Editor assigned: 26-Jul-2021 / PreQC No. JMSN-22-15953(PQ) / Reviewed: 05-Jan-2022 / QC No. JMSN-21-15953 / Revised: 15-Jan-2022 / Manuscript No. JMSN-22-15953(R) / Accepted Date: 24-Jan-2022 / Published Date: 31-Jan-2022 DOI: 10.4172/jmsn.100031
Abstract
An estimate of the thermal conductivity coefficient of ferromagnetic κ at temperatures lying near the point of phase transition, i.e. at temperature T = Tc −ε , where ε <<Tc . made. The calculations are based on the quasi-classica kinetic equation method, and it shows that
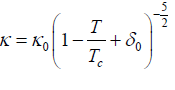 with a critical index equal
with a critical index equal 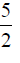 and
and 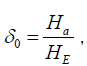 where Ha − field of magnetic anisotropy, HE − exchange field.
where Ha − field of magnetic anisotropy, HE − exchange field.
Keywords
Magnetic phase temperature; Quasi-classical kinetic equation; Thermal conductivity factor.
Introduction
When carefully acquainted with a large number of literary sources dedicated to the description of the ph ysical properties of magnetic substances at temperatures in the area of magnetic phase transition [1- 10], despite the nearly century-long history of this issue, we have not found an analytical calculation of the temperature dependence of the ferromagnetic thermal conductivity coefficient κ (T ) at temperature 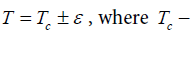 is Curie’s temperature, and ε<<Tc . Although the general theory of phase transitions, both macroscopic (ref. [11] – [13]) and microscopic (see [14] – [18]) long been constructed, some questions for some reasons have been overlooked and not covered in the literature. That is why the purpose of this communication is to close this small gap associated with calculating of thermal conductivity in the area of magnetic phase temperature. Experimental measurements devoted to this subject , which is typical of any other physical characteristics in the field) indicate a strong growth of thermal conductivity
is Curie’s temperature, and ε<<Tc . Although the general theory of phase transitions, both macroscopic (ref. [11] – [13]) and microscopic (see [14] – [18]) long been constructed, some questions for some reasons have been overlooked and not covered in the literature. That is why the purpose of this communication is to close this small gap associated with calculating of thermal conductivity in the area of magnetic phase temperature. Experimental measurements devoted to this subject , which is typical of any other physical characteristics in the field) indicate a strong growth of thermal conductivity  at T = Tc the value of which can be calculated analytically, and which, as we shall see, has an end value. Looking ahead, we note that the value of this maximum is determined by the value of the
at T = Tc the value of which can be calculated analytically, and which, as we shall see, has an end value. Looking ahead, we note that the value of this maximum is determined by the value of the  where κ0 − characteristic thermal conductivity coefficient, Ha− field of magnetic anisotropy,
where κ0 − characteristic thermal conductivity coefficient, Ha− field of magnetic anisotropy, 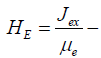 exchange magnetic field, Jex− energy of exchange interaction, μe− Bore’s magneton.
exchange magnetic field, Jex− energy of exchange interaction, μe− Bore’s magneton.
Hamiltonian interactions at T < Tc
In the theory of phase transitions concerning the unbalanced properties of the substance, the necessary condition is always to know the appropriate time of relaxation.
Specifically, when it comes to thermal conductivity calculation κ need to have an idea of the relaxation time, which in the case of ferromagnets is due to the interaction between magnon and phonon subsystems.
Since we are talking about a gas-kinetic approach, the basic estimated formula in the isotropic case should look according to the general rules of its receipt.
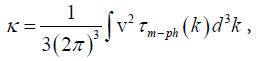 (1)
(1)
where 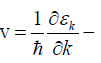 group speed of the magnons,
group speed of the magnons,
 their dispersion, h − Planck’s constant, k − wave vector of magnon, k − Boltzmann’s constant,
their dispersion, h − Planck’s constant, k − wave vector of magnon, k − Boltzmann’s constant, 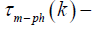 magnon - phonon time of relaxation.
magnon - phonon time of relaxation.
Everywhere we will use the energy system of units, in which we believe that Boltzmann’s constant kB =1 and for the sake of convenience we will put also as the Planck’s constant h =1 . This will not lead to confusion in dimensions (see below).
Because the group speed of the magnon is  it’s always possible to think that d3k = 4π k 2dk , and therefore from (1) we have
it’s always possible to think that d3k = 4π k 2dk , and therefore from (1) we have
 (2)
(2)
where the lower limit of integration can only be defined after analysis energy and impulse laws for a particular magnon-phonon interaction.
With this goal we need to introduce the energy of magnon – phonon interaction is easy to record for isotropic case considering the crystal symmetry to be cubic.
We can present the relevant interaction in the only form, as
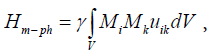 (3)
(3)
where γ − is dimensionless strict constant order of units, M=(Mi) is the order parameter, i.e. the magnetic moment of the unite volume of the ferromagnet  deformation tensor, u = (ui) − is vector of deformation, V − is the body volume.
deformation tensor, u = (ui) − is vector of deformation, V − is the body volume.
By the way, it’s worth noting that interactions like 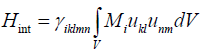 in crystals with any spatial symmetry it’s can’t be.
in crystals with any spatial symmetry it’s can’t be.
It’s connected due to the physical fact that any type of interaction must satisfy the rule of invariance in relation to the time inversion operation, that  , where t − is the time.
, where t − is the time.
Because the vector of magnetism is an axial vector in relation to the replacement of inversion time t →−t i.e. 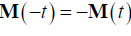 , this indicates that this type of interaction is not possible, although it should be noted that this type of interaction is not prohibited by the laws of energy and momentum.
, this indicates that this type of interaction is not possible, although it should be noted that this type of interaction is not prohibited by the laws of energy and momentum.
To rewrite the interaction (3) in the language of operators of birth and destruction of magnons and phonons, it must be presented in a secondary – quantization form. To do this, we should remember that in accordance with Holstein-Primakov’s transformations, we have the right to write down that
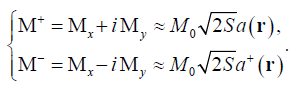 (4)
(4)
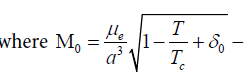 is spontaneous magnetism in the Curie’s temperature area, S − is the spin of atom
is spontaneous magnetism in the Curie’s temperature area, S − is the spin of atom  is the operator of the birth (destruction) of the magnon at the local point with a radius - vector r. The expression for the dimensionless value 0 δ are given below.
is the operator of the birth (destruction) of the magnon at the local point with a radius - vector r. The expression for the dimensionless value 0 δ are given below.
In the k − presentation the operators of berth (destruction) of magnon we can presented as a Fourier’s row
 (5)
(5)
where N − full number of atoms in the magnet.
The vector of deformation is also easily carried out with the help of a simple Fourier - decomposition
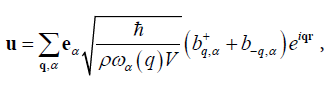
where αe − is an polarization vector of phonon, index a is specify to three possible polarization branches: two acoustic (longitudinal and transversal) and one optical, ρ − is the density of ferromagnet, q − is a wave vector of phonon  is an operator of berth (destruction) of phonon with the wave vector q and polarization a,
is an operator of berth (destruction) of phonon with the wave vector q and polarization a, 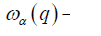 is phonon dispersion, where index α =1,2,3 .
is phonon dispersion, where index α =1,2,3 .
For the acoustical phonons the dispersion is  where ct,l − is accordingly the longitudinal and transversal speed of the sound. Single designation will be used everywhere below cs . For optical phonons, we will believe that
where ct,l − is accordingly the longitudinal and transversal speed of the sound. Single designation will be used everywhere below cs . For optical phonons, we will believe that 
According to (6) the components of the tensor deformations can then be presented as a form of
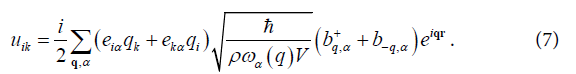
After substitution (5) and (7) in definition (3) as a result of simple rule-adjusted changes
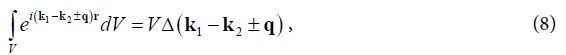
we come to the interaction in the form
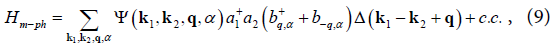
Where the abbreviation c.c. means a complex - conjugated value and indices 1,2 at birth and destruction operators mean a reduction i.e. 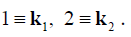 At the same the amplitude of interaction is defined
At the same the amplitude of interaction is defined
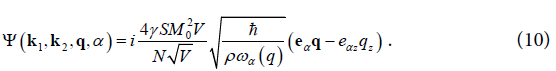
It is clear that in the absence of interaction the main Hamiltonian can be recorded as
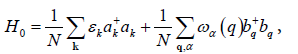
where k ε and (q) α ω are determined above.
Calculating the relaxation time in the field of phase transition temperature
We can use the quasi-classical kinetic equation (see, for example, refs. [26] – [29]) in the form

where nk − is an collision integral, nk − function distribution of
magnons, fq − is an equilibrium distribution function of the phonons. The phonons we are assuming an thermostat. At high temperatures in the region of Curie’s temperature it can presented in following

Before moving on to specific calculations, it is worth noting that
the equation (11) will be fairly ̧ if the condition is met 
where 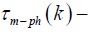 is the magnon – phonon relaxation time.
is the magnon – phonon relaxation time.
As we shall see later (see formula (20)), this condition is fulfilled near the phase point and it is quite possible to use the equation (11).
According to the interaction (9) the integral of collisions will look like this 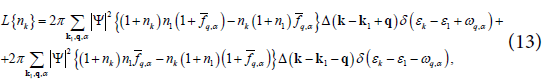
where the presence of delta function automatically takes into account the law of energy conservation. According to (13) the relaxation time in the “tau - approximation” will be
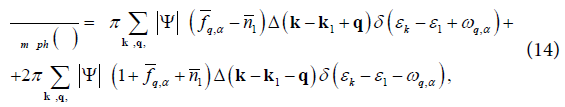
where the equilibrium function distribution of magnons at the temperatures near the Curie’s point is

As a result, instead of (14) we get

A simple analysis of energy and momentum laws, taking into account the rules of transition from summation to integration

allows us to get the following interim expression

where the parameters are
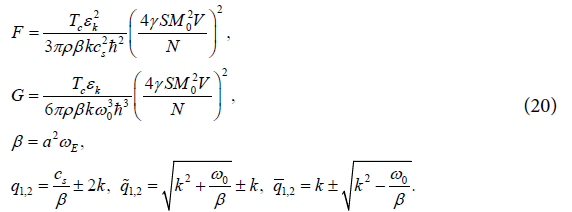
In fact, simple but rather cumbersome calculations of the integrals featured in (19) lead to the next final result for the time of relaxation of interest to us

where q1,2 identified in (20), and the wave vector of the magnon should be “squeezed” in the segment

Expression analysis (21) shows that only the large values of the magnon wave vector will make the greatest contribution to the thermal conductivity coefficient. This means that the last term in the expr. (21) will be the most significant. Leaving only it and substituting the result in the general definition (2), we get

Due to the convergence of this integral, we can put the lower limit of integration to zero, and the upper limit - infinity.
Assuming that at a point c T = T over an extremely short period of time τ , which is significantly less than all relaxation times, an instant magnetic order appears, then we have the right to write down the following expression for the thermal conductivity factor
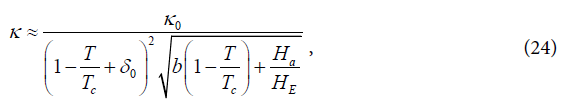
where the coefficient

Formulae (24), (25) give an answer to the question posed at the beginning of the article, and the dimensionless parameter 0 δ , which appears in the definition M0 (see formula (4)) according to (24) is

It would seem that when c T = T we have a small but finable value of the order parameter. However, it should be understood that we are talking about temperatures just below the point of phase transition, that is, it should be considered c T = T −ε that, and the field of magnetic anisotropy behaves like a

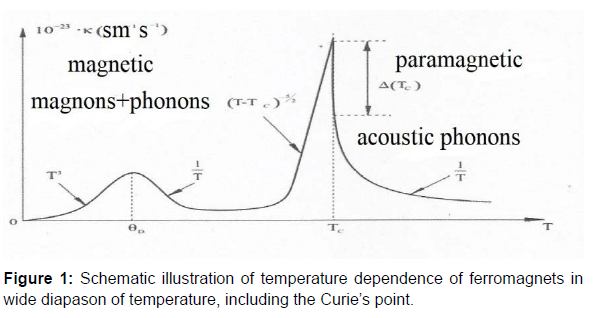
That is, near the point of Curie begins to form the energy of magnetic anisotropy and thermal conductivity should increase sharply, which is in accordance with the general principles of the theory of phase transitions. Its maximum value can be estimated as

The thermal conductivity of the paramagnetic at T > Tc
It is quite clear that in this range of temperatures, not much far from the melting point, the magnetic moment in the absence of an external magnetic field is zero, and therefore no magnetic interactions should not be about, as well as energy of magnetic anisotropy. This means that heat transfer in the paramagnetic phase can only be carried out thanks to acoustic phonons, even if there is no crystalline order. This is clearly a burden of the fact that there is always a heterogeneous density of ρ (r) material, which within the theory of elastic deformation can be presented as a ratio 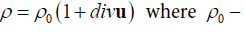 the unperturbed density of the material.
the unperturbed density of the material.
This means that to calculate the only time in this case, the phonon - the phonon relaxation, we can come from an isotropic Hamiltonian species (see. [27])

where θ − some characteristic energy, in order of magnitude corresponding to Debai’s energy θD . Substituting here (7) with account (8), we find 

Interaction amplitude is
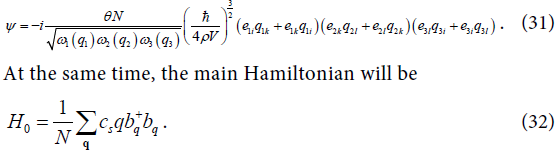
According to (30) the integral of the collisions will be
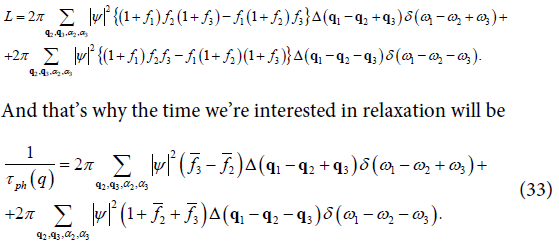
Because
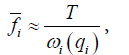
that of (33) we have
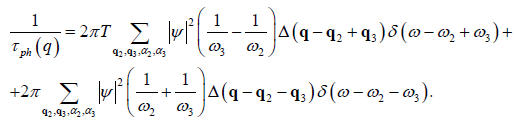
where ω =ω (q) .
Taking into account the laws of preservation and after the transition from summation to integration under the rule (18), taking into account the explicit expression for the amplitude of interaction (31) and taking into account the properties of the delta - functions we get as a result of integration


Substituting (34) in the overall expression for the thermal conductivity ratio

For a numerical estimate κ it can be assume that  where a − is some average interatomic distance. Substituting in (35) specific numerical values
where a − is some average interatomic distance. Substituting in (35) specific numerical values

we get from here 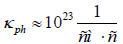 If put in (35) T = Tc and compare with (28), we’ll see that
If put in (35) T = Tc and compare with (28), we’ll see that

Therefore, the jump in thermal conductivity in the transition from the paramagnetic phase to the magnetic will be the magnitude of

Ratios (36), (37) allow us to build dependence κ (T ) in a wide interval of temperature up to melting temperature, which is reflected in (Figure 1).
Conclusion
In conclusion, it is worth paying attention to some of the results above.
1. Using a quasi-classical kinetic equation, the thermal conductivity ratio of ferromagnetic in the vicinity of phase temperature is calculated;
A critical staid growth index has been found and it’s shown that

A comparison of the phonon thermal conductivity in the paramagnetic phase T > Tc with thermal conductivity in the magnetic phase at T ≤ Tc and calculated the jump in thermal conductivity at the point T = Tc
A graphic interpretation of the result in a wide range of temperatures is given.
References
- Sinoviev VE, Abelsky SS, Sandakova MI (1974) The thermal properties of iron and solid silicon solutions in it near Curie point. J Exper Theore Phys 66: 354-359.
- Ilyinov SA, Taluz SG, Sinoviev VE, Bautin SP (1984) Measuring the temperature in subsecond heating mode. High Temp Phys 22: 709-714.
- Belov KP, Zaitseva MA, Ped’ko AV (1959) Magnetic Properties of Gadolinium Oxides. Soviet Physics JETP 36:1672-1679.
- Iwase A, Hamatani Y, Mukumoto Y, Ishikawa N, et.al. (2003) Anomalous shift of Curie temperature in iron-nickel Invar alloys by high-energy heavy ion irradiation. Nucl Instrum Methods Phys Res B 209: 323-328.
- Ginsburg VL, Landau LD (1950) On the theory of superconductivity. J Exp Theor Phys 20:1064-1072.
- SO Gladkov (2019) On a Nonlinear Effect in the Superconductivity Theory. Solid State Phys 61:1955-1959.
- Fong YF, Hao-Kun Li, Zhao R (2019) Phonon teat transfer across a vacuum through quantum fluctuations. Nature 576: 243-247
- Schwab K, Henriksen EA, Worlock JM, ML Roukes (2000) Measurement of the quantum of the thermal conductance. Letters to Nature 404: 974-976.
- Jou D, Casas-Vasquez J (2015) Heat transfer and thermodynamics: A foundational problem in classical thermodynamics and in contemporary non-equilibrium thermodynamics. J Non-Equil Thermody 11:131-136.
- Gladkov SO, Kaganov MI (1981) To the Theory of Relaxation of Nuclear Spins in Ferromagnets. J Exp Theor Phys 80:1577-1585.
- Gladkov SO (1982) Relaxation in Ferromagnetic Metals. J Exp Theor Phys 83: 806-809.
Indexed at Google Scholar Crossref
Indexed at Google Scholar Crossref
Indexed at Google Scholar Crossref
Indexed at Google Scholar Crossref
Indexed at Google Scholar Crossref
Indexed at Google Scholar Crossref
Citation: Gladkov SO (2022) On the Thermal Conductivity of Magnets near the Point of Phase Transition. J Mater Sci Nanomater 6: 031. DOI: 10.4172/jmsn.100031
Copyright: © 2022 Gladkov SO. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 1726
- [From(publication date): 0-2022 - Dec 22, 2024]
- Breakdown by view type
- HTML page views: 1384
- PDF downloads: 342