Journal of Speech Pathology & Therapy
Open Access

Background

The air pressure in the lungs during speech is the primary energy source for the acoustic energy produced by the human voice. This air pressure is commonly also referred to as sub glottal pressure (Psg) or tracheal pressure, though these are technically slightly different. We will hereafter favor the term sub glottal pressure. (The term ‘pressure‘, as used herein, refers to the low frequency component of the pressure, with acoustic energy removed.)

However, because of the inaccessibility of the lungs, the sub glottal air pressure is difficult to determine clinically during speech or singing, and especially difficult to measure in real-time as would be desirable in a voice training application.

However, it is generally accepted that control of the sub glottal pressure is important clinically. According to Ronald Baken and Robert Orlikoff in Clinical Measurement of Speech and Voice [1], “Measurement of sub glottal pressure is potentially of great diagnostic and therapeutic value in a wide range of speech and related disorders.” They add “there is no simple direct and convenient technique for actually measuring subglottal pressure during speech.” (as of the publication of their book in the year 2000).

A low sub glottal pressure will invariably cause a weak voice, while the use of an abnormally high subglottal pressure, sometimes referred to as vocal hyper function [2], can result in vocal fold strain and a number of voice disorders [3].

Populations at risk for vocal hyper function include singers, cheerleaders, actors, athletic coaches and teachers. Tanner [4] maintains that “Disorders related to vocal strain and abuse include nodules, polyps, and contact ulcers. They may occur on one or both vocal folds. They are common in people who do a lot of talking or singing and who otherwise strain their vocal folds.”

Most previous attempts to directly measure lung pressure during speech have employed highly invasive techniques that are not practical for routine clinical measurements or for speech training exercises, such as the use of a tracheal puncture, in which a hypodermic syringe connected to a system for recording air pressure is inserted between the cartilaginous rings of the trachea [5]. Though useful for research purposes under appropriate medical supervision, this method would be rejected by most clinicians and patients for routine screening or speech training exercises.

Another invasive technique that has been used for measuring subglottal pressure during speech consists of inserting a miniature pressure transducer through the glottis into the trachea [6]. In this method, the vocal folds and nearby tissues must be anesthetized to suppress the glottal closure reflex that prevents the potentially fatal aspiration of food or other foreign bodies. The need for anesthetization and the potential complications from placing a foreign body into the subglottal space make this method also generally unacceptable for routine screening or speech training.

The interpolation procedure for estimating subglottal pressure

It is well known that the subglottal pressure during speech can be estimated by recording the peak intraoral air pressure during an unvoiced bilabial consonant (as /p/ in English) [7]. This method is based on the fact that if the outlets of the oral chamber are closed for producing the bilabial plosive (lips and velopharyngeal passage both closed), and the glottis is open for the articulation of the unvoiced consonant, the intraoral pressure will equalize with the tracheal pressure in a matter of milliseconds, or tens of milliseconds at the most. We will refer to this method as the interpolation technique. As used by Rothenberg [7], and later proposed by Smitheran and Hixon for clinical applications [8], the subglottal pressure during a vowel produced between two unvoiced bilabial consonants can be estimated by interpolating between the intraoral pressure peaks during the two neighboring consonants. We refer to this method herein as the interpolation technique.

For completeness, it should be mentioned that a similar method has been used experimentally in which the oral vocal tract is closed by a mechanical valve, and the intraoral pressure recorded [9]. However, problems with the method and the necessity of speaking into a mechanical valve have kept it from being used extensively during natural speech.

However, the interpolation technique as originally implemented does not provide a real-time measurement. It has been used primarily for the analysis of previously recorded speech or singing, using a digital computer to implement the interpolation algorithm. One result of this limitation is that the interpolation technique as implemented according to the method originally proposed by Rothenberg could not be used conveniently for biofeedback in voice training exercises. In addition, the technique implemented according to this protocol is cumbersome when used in routine speech testing.

The repeated syllable algorithm used in the paper by Rothenberg [7] was designed to determine an estimate of the subglottal pressure during inverse filtered glottal airflow waveforms produced with different vowels, fundamental frequencies, degrees of vocal fold abduction and subglottal pressures. However, the application so described was not meant to exclude the use of the general method of interpolation for estimating the subglottal pressure in fluent speech or singing. The underlying principle is that subglottal and intraoral pressures equilibrate during the closure phase of an unvoiced stop consonant. This principle is valid during all speech and singing.

In this paper, it is proposed that the interpolation technique can be adapted to real time measurements in continuous speech or singing, and a practical system for doing this is outlined.

Real time interpolation of subglottal pressure during speech or singing

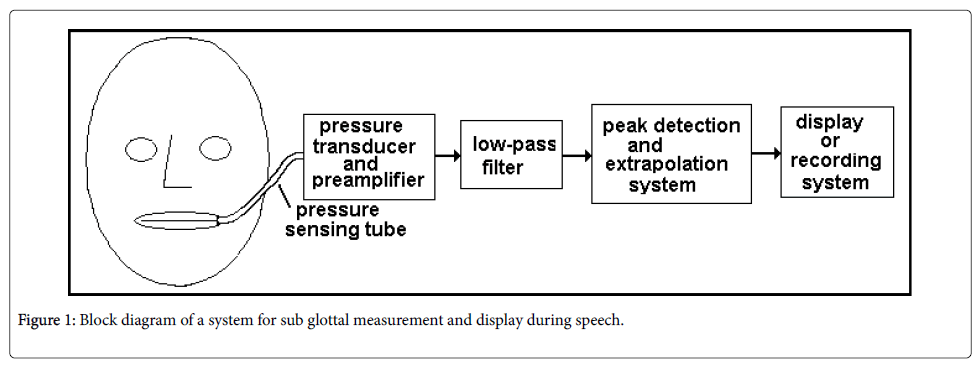
Figure 1 shows the basic elements of a system for estimating subglottal pressure from the intraoral pressure, assuming the intraoral pressure being used is the pressure behind the closure of a bilabial stop.

Figure 1: Block diagram of a system for sub glottal measurement and display during speech.

In Figure 1, the intraoral pressure is sampled by a fine tube inserted at the corner of the mouth or between the lips. The tube leads to a pressure transducer and associated preamplifier capable of measuring pressures in the range found intraorally (A miniature transducer inserted in the mouth could also be used).

Since the output of the transducer/preamplifier, in addition to the low frequency pressure signal that represents the subglottal pressure, can be expected to contain unwanted acoustic pressure information, a low pass filter can be used to eliminate the acoustic pressure variations. Since the acoustic pressure variations in the mouth are generally above about 50 Hz, the low pass filter might have a cutoff frequency of approximately 30 to 40 Hz.

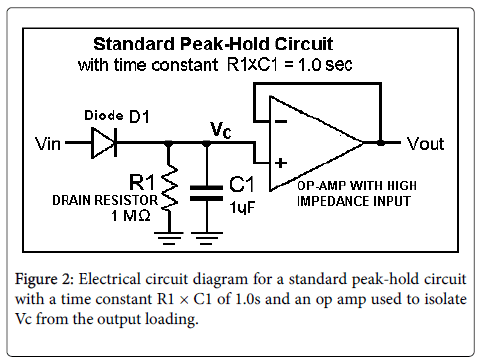
Since it is the peak of the oral pressure pulse during the stop closure that approaches the subglottal pressure, there must be a functionality that detects this peak and holds it for a period of time sufficient for it to be measured. This functionality can be accomplished by a digital computer program, but we suggest here an electronic circuit commonly called a peak detector, or peak-hold circuit, as shown in its simplest form in Figure 2.

Figure 2: Electrical circuit diagram for a standard peak-hold circuit with a time constant R1 × C1 of 1.0s and an op amp used to isolate Vc from the output loading.

In the standard peak-hold circuit in Figure 2, the diode D1 conducts whenever the input voltage Vin is greater than the voltage of C1, bringing Vc and Vout to the value of Vin, assuming an ideal diode D1.

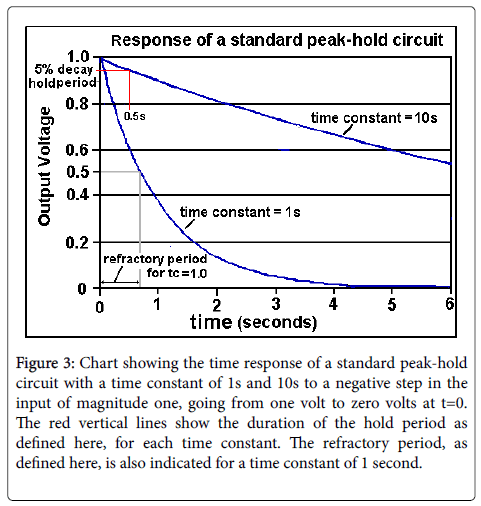
The circuit has a response that begins to decay immediately after the removal of the peak in Vin. If the voltage Vin is small with respect to the capacitor voltage Vc during the post-peak decay, the decay is exponential with a time constant equal to R1 × C1, as shown in Figure 3 for two values of the time constant R1 × C1.

Figure 3: Chart showing the time response of a standard peak-hold circuit with a time constant of 1s and 10s to a negative step in the input of magnitude one, going from one volt to zero volts at t=0. The red vertical lines show the duration of the hold period as defined here, for each time constant. The refractory period, as defined here, is also indicated for a time constant of 1 second.

We will consider that the time during which the output of a peakhold circuit is within 5% of the detected peak value as a ‘Hold’ time. The annotation in Figure 3 illustrates that the output of a standard peak-hold circuit holds the detected peak value to within 5%, for a period of time of approximately 1/20 x the time constant.

A circuit with a time constant of 1.0 seconds will take 1.0 seconds to decay from 1.0 to 1/e=0.37 sec, and a period of approximately 0.7 seconds to decay to half of its peak at t=0). During this period of exponential decay, the circuit will not detect and register other peaks that are less in amplitude than the circuit output. We will refer to this period as a refractory period.

A ‘refractory period’ is generally defined as ‘a period immediately following stimulation during which a nerve or muscle is unresponsive to further stimulation. It is often applied to other physiological responses in which a recovery is required after a response. In other words, a peak-hold circuit requires a recovery from a given peak pressure in order to respond to a subsequent peak.

Since the subglottal pressure is a slowly changing variable, a refractory period of T seconds means that pressure peaks larger than 50% of the previous peak (our definition of a viable pressure peak) will not be detected for T seconds after that previous peak.

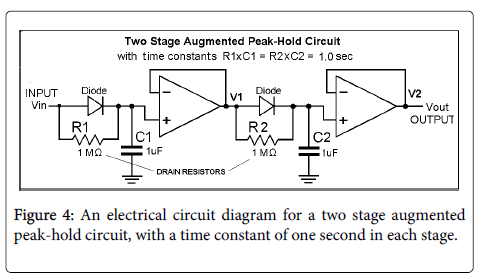
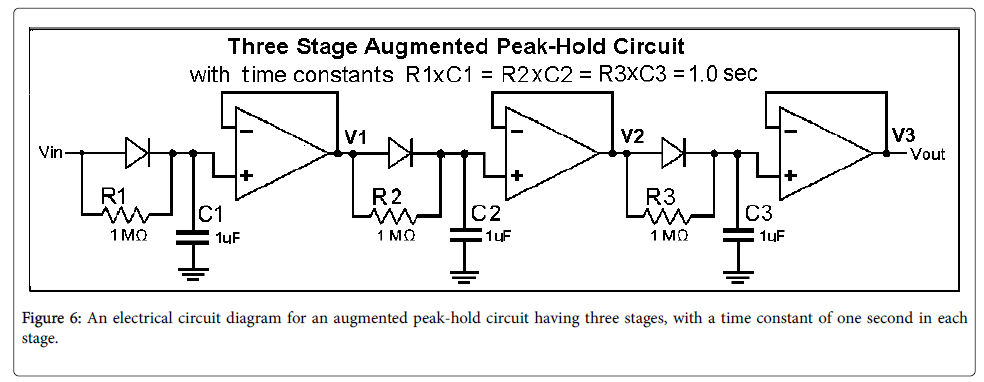
It should be noted that there is a conflict between the desired hold time, which is preferably large, and the duration of the refractory period, which is preferably small. To solve the problem of a conflict between the desired hold time and the refractory period, this paper presents a modification of a standard peak-hold circuit in which the drain resistor is returned to the voltage input to the diode instead of to ground, as are R1 and R2 in Figure 4. We will refer to such a circuit as an augmented peak-hold circuit, or APH. Figure 4 shows a two stage APH. Using a multistage augmented peak-hold circuit slows the initial discharge of the hold capacitors, C1 or C2 in the figure, thus increasing the period in which the output is held near the peak value (the hold period). The hold period will be shown to increase with the number of stages.

Figure 4: An electrical circuit diagram for a two stage augmented peak-hold circuit, with a time constant of one second in each stage.

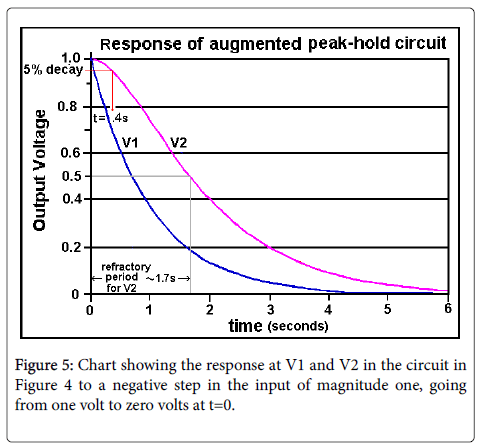
Figure 5 shows the response of a two-stage APH. The hold time (time with the output within 5% of the peak) has been increased by a factor of approximately 4 in the two stages APH, with only a small increase in the refractory period. The hold time can be further increased by using an additional stage of APH, as in Figure 6.

Figure 5: Chart showing the response at V1 and V2 in the circuit in Figure 4 to a negative step in the input of magnitude one, going from one volt to zero volts at t=0.

Figure 6: An electrical circuit diagram for an augmented peak-hold circuit having three stages, with a time constant of one second in each stage.

It should be noted that cascading two stages of the standard peakhold circuit in Figure 2 would have no such effect, that is, an Augmented Peak-Hold circuit is required. It can also be noted in passing that a roughly similar increase in the hold period of a standard Peak-Hold circuit may be obtained by adding an inductance in series with R1 of the standard sample hold circuit, to delay the drain of the capacitor charge.

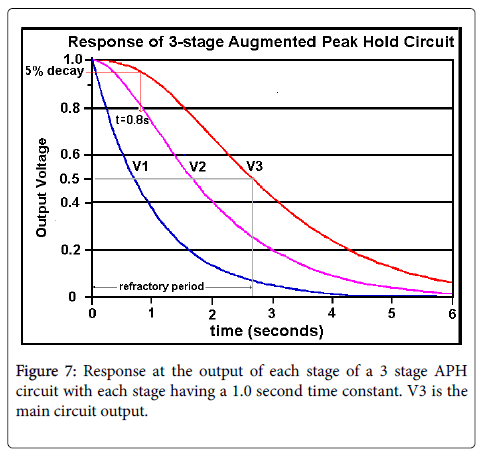
The operation of the circuit in Figure 6 is illustrated in Figure 7. The curves in the chart of Figure 7 show the voltage at the outputs of the three stages, referred to as V1, V2 and V3 respectively, after the input Vin leaves its peak value and goes quickly to zero (a negative step function).

Figure 7: Response at the output of each stage of a 3 stage APH circuit with each stage having a 1.0 second time constant. V3 is the main circuit output.

Figure 7 shows that with three APH sections, with all sections having the same time constant equal to 1.0, the output (V3) is still at over 95% of the peak value after 0.8 seconds (rounded to one significant figure). This may be considered a reasonable value for realtime observation. The refractory period is approximately 2.7s. This duration is somewhat too long for speech, in which pressure peaks can be more closely spaced, as in the word “papa” in English. However, the extension of the hold time can be further increased, without a proportionate increase in refractory period, with more sections cascaded.

As can be seen in Figure 7, as cascaded stages are added having the same time constant, the delay caused by the filter increases approximately in proportion to the number of stages.

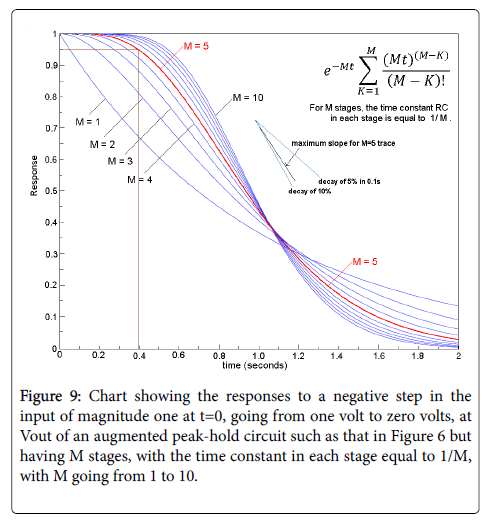
This undesirable result of adding cascaded stages can be compensated for by using a time constant that varies inversely with the number of stages in the filter. For example, if the time constant for a single stage filter is assumed to be one second, then the time constant for each stage of a comparable M-stage filter would then be 1/M. The response of such a filter would be as in Equation 1, where Equation 1 represents the response of an M-stage filter to a negative step of unity amplitude (voltage going from 1 to 0 at t=0) for M stages, with the time constant for each respective stage equal to 1/M (Figure 8).

Figure 8: The functions in Equation 1 are plotted for values of M ranging from 1 to 10.

In Figure 9, the trace for M=5, a value to be used below, is shown in red. This selection for M exhibits a hold time of approximately 0.4s and a refractory period with a duration of approximately 0.9s. From informal experiments performed by the author, these values meet the requirements for real-time measurements during speech or singing, though research would be required for optimization.

Figure 9: Chart showing the responses to a negative step in the input of magnitude one at t=0, going from one volt to zero volts, at Vout of an augmented peak-hold circuit such as that in Figure 6 but having M stages, with the time constant in each stage equal to 1/M, with M going from 1 to 10.

Figure 9 shows that increasing the number of stages, M, reduces the refractory period by increasing the rate at which the output decays after an input pulse. As shown by the annotation in the figure, the maximum decay rate can be estimated from the graph to be approximately 9.5% in 0.1 second, and the average decay rate after the hold period is roughly half of that. These figures show that 4 or 5 or 6- stage APH circuit would fit our experimentally determined criteria, and this conclusion has been confirmed by tests using a 5-stage APH circuit, though the optimal number of stages and the optimal values of the RC time constants in each stage should be determined by further testing.

Step response with a 200 ms time constant

For the following traces, an analog implementation of the circuit of Figure 1 was used, with the peak detection and extrapolation module an Augmented Peak-Hold, with the number of stages chosen as 5. The low pass filter was a 6-pole Bessel linear phase filter, with the -3 dB cutoff frequency chosen as 30 Hz. The system was calibrated using a Dwyer Magnehelic pressure gauge.

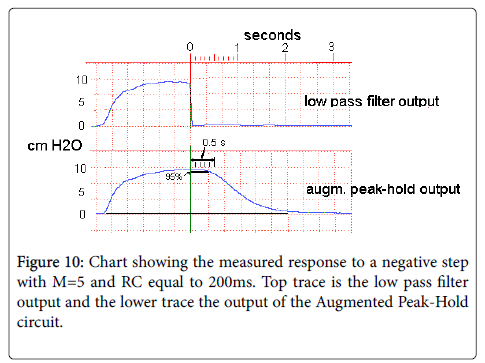
The RC time constant in the augmented peak hold circuit in each stage was 200 ms, which should result in a 95% hold time of approximately 400 ms according to the plot in Figure 9.

For Figure 10, an adult male subject produced a single /pa/ syllable, with the intraoral pressure at the release of the /p/ dropping essentially instantaneously from almost 10 cm H2O to zero. The measured response in Figure 9 is similar to the response predicted mathematically in Figure 8 for these parameters, with the 95% hold time, as marked on the lower graph, roughly similar to the value predicted from Figure 8.

Figure 10: Chart showing the measured response to a negative step with M=5 and RC equal to 200ms. Top trace is the low pass filter output and the lower trace the output of the Augmented Peak-Hold circuit.

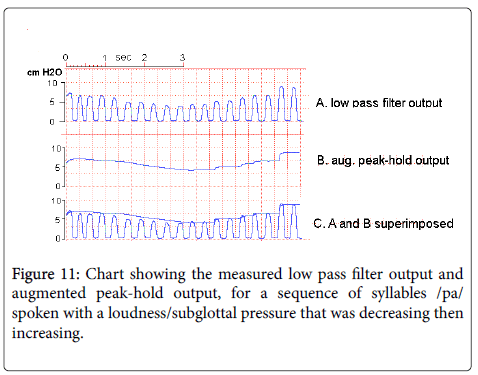
For Figure 11, an adult male phonetically trained speaker produced a sequence of concatenated /pa/ syllables with a falling-rising-fallingrising effort at an attempt to produce a maximum rate of subglottal pressure change, so as to test the capacity of the system to follow the decreases and increases of subglottal pressure. The increases of pressure were recorded successfully, except for the jumps at each increase in pulse height caused by the inability of the system to anticipate the increase.

Figure 11: Chart showing the measured low pass filter output and augmented peak-hold output, for a sequence of syllables /pa/ spoken with a loudness/subglottal pressure that was decreasing then increasing.

However, it can be seen in the figure that the decreases in subglottal pressure were sometimes too fast for the system to follow accurately, as. A reduction in the time constant of the augmented sample hold circuit, say from the value used of 200ms to 150ms, would result in an improved ability of the circuit to follow pressure decreases. An increase in the number of stages (noted as M) would also have this effect.

Such a decrease in the time constant may not be required in practice since the rate of subglottal pressure change is limited in actual speech.

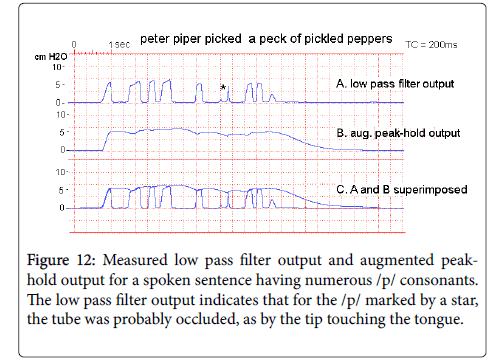
To illustrate the response of the same system to the subglottal pressure variation found in actual speech, Figure 11 shows the low pass filter output and augmented peak-hold circuit outputs for the same adult male subject, speaking the sentence “Peter Piper picked a peck of pickled peppers” spoken at a conversational voice level.

Limitations of an augmented peak-hold circuit

In addition to the dynamic limitations sketched above, the primary limitation of the APH approach for estimating subglottal pressure during speech or singing is the necessity to use speech or singing materials having /p/ consonants. In some testing contexts it will be possible to use repeated nonsense syllables or repeated words containing one or more occurrence of /p/. In other cases it may be possible to contrive more meaningful material rich in occurrences of /p/, as including words such as “papa” or “pepper”.

Another limitation of an APH circuit is the forward voltage of real diodes. In a 5-stage circuit, for example, the signal passes through 5 diodes, with each diode adding an increment to the error in the circuit output as a representation of the peak pressure. However, the diodeinduced error can be minimized by using Schottky diodes having a forward voltage of only a few tenths of a volt, and partially compensating for the error during a calibration process.

Also, the peak detection and hold system described here cannot perform a number of desirable complex operations involving pressure peaks. In contrast, a microprocessor version of the peak detection and hold system could be programmed to detect and measure a number more than one of such peaks and perform more complex operations involving such peaks, such as averaging or interpolation. However, it is envisioned that the analog circuit described in this application would be more economical to produce than a microprocessor version, and be adequate for many applications, such as biofeedback in training for vocal effort correction.

Suggested procedures for use in testing

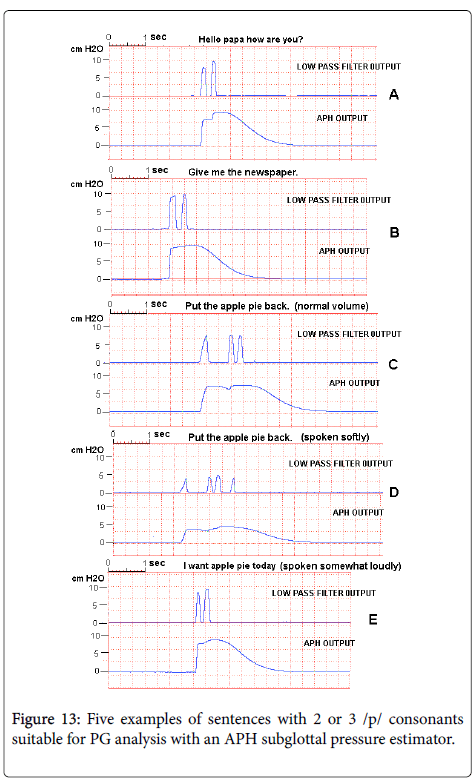
Though the test results shown in Figures 10 and 11 illustrate well the action of an APH circuit with connected speech, it is not likely that sentences with that many instances of /p/ will be convenient in a test or training situation, nor will be needed for an evaluation of subglottal pressure. The primary function of an APH circuit is to hold a measure value of Psg for an interval sufficient to allow it to be recorded either visually or instrumentally. For this to happen, even a single instance of /p/ might be sufficient, with the APH circuit holding the measured value for approximately a half second [1-4].

However, sentences containing two closely spaced instances of /p/, would hold the measured value for approximately a second, and are preferred. This would mean that a sentence including a word with two /p/s could be used, irrespective of the remaining phonetic content. For example, there are numerous words in English with two /p/s, such as papa, paper, newspaper, pepper, purpose, pineapple, etc. Two such words are contained in the “Peter Piper” sentence. Expressions containing a sequence of two ’p’ words can also be used, such as ‘apple pie’ in English, or ‘Pourquoi pas?’.

Figure 12 shows the low pass filter output and APH output for a number of English sentences spoken by a male adult speaker filling these requirements. The sentences in examples C, D and E of Figure 12 were spoken respectively at a normal conversational voice level, a somewhat soft voice level, and a somewhat high voice level. The traces in Figure 12 show that the APH output in each case reflects the voice level.

Figure 12: Measured low pass filter output and augmented peakhold output for a spoken sentence having numerous /p/ consonants. The low pass filter output indicates that for the /p/ marked by a star, the tube was probably occluded, as by the tip touching the tongue.

In each case in Figure 13, the APH output is held long enough at the subglottal pressure for an observation to be made. However, it should be noted that the unit used for these traces was provided with a manual Hold capability triggered by a pushbutton switch, so that it was only necessary to have Psg approximated long enough at the APH output after the occurrence of a /p/ for the Hold button to be depressed.

Figure 13: Five examples of sentences with 2 or 3 /p/ consonants suitable for PG analysis with an APH subglottal pressure estimator.

Error caused by nasal airflow during the /p/

The method used in the examples above assumes that there is not enough airflow during the /p/ closures to cause a significant pressure drop across the glottis. Such airflow can occur in consonants that are produced nasalized, as when speaking very low, or in some types of disordered speech. If it is suspected that this is occurring, it is a good idea to pinch the nares shut during the speech or uses a nose clip. Nose clips for spirometry or for swimming that are adequate for this purpose can be located through any internet browser [5-9].

The presence of nasal airflow can be checked by obstructing the nares during the testing, as by pinching the nares or using a nasal clamp. If significant nasal airflow is present, the meter reading will increase with the nares occluded.

Languages with no /p/ consonants

It has been reported that in some Native American languages there are no unvoiced bilabial stops. However, subjects in this class will usually have a proficiency in an Indo-European language such as English that has the stops available.

The often cited concept of ‘vocal effort’ has been occasionally quantified as a subjective rating (yielding what might be better referred to as subjective vocal effort) or, alternatively, by the Sound Pressure Level (SPL) at a fixed, standardized distance from the mouth, in a hopefully sound treated room or enclosure. However, in many such cases, a better measure of vocal effort would have been a physiological variable such as the subglottal pressure, or a compilation of a number of physiological variables, including Psg. The apparent reason for not using Psg or other physiological variables is the difficulty in measuring those variables during speech or singing. However, this paper outlines one possible system that accomplishes this end for subglottal pressure, and shown that reasonable estimates of Psg can be obtained noninvasively during speech or singing. Thus there is no reason to use a subjective rating or SPL, when Psg would be more appropriate.

As one example, if a teacher’s voice is fatigued as the day progresses, one might expect that the larynx might become less efficient as a sound source. Thus the measured SPL, for the same vocal effort, might decrease. Using SPL as a measure of vocal effort would lead to the erroneous conclusion that vocal effort has decreased as the day progressed. We would hope that in future research involving vocal effort, researchers either use the subglottal pressure, or some other physiological variable, as the underlying variable, or give a satisfactory rationale for not doing so.

A preferred display modality for the estimated subglottal pressure has not been specified in this paper. It would be hoped that future research would determine a display that could be used conveniently by children and adults for biofeedback. Research is also needed on optimizing the values of the Augmented Peak Hold circuitry, namely, the time constant and the number of stages, as well as on other alternatives for accomplishing this function.