Editorial Open Access
Non-metallic Particles Manipulation in Liquid Metals During Electromagnetic Processing
Zhi Sun*
Pyrometallurgy Research Centre, School of Chemical Engineering, The University of Queensland Brisbane, 4072, Australia
- *Corresponding Author:
- Zhi Sun
Pyrometallurgy Research Centre
School of Chemical Engineering
The University of Queensland Brisbane
4072, Australia
E-mail: zhisun@126.com
Received Date: July 29, 2012; Accepted Date: August 02, 2012; Published Date: August 06, 2012
Citation: Sun Z (2012) Non-metallic Particles Manipulation in Liquid Metals During Electromagnetic Processing. J Powder Metall Min 1:e102. doi: 10.4172/2168-9806.1000e102
Copyright: © 2012 Sun Z. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Powder Metallurgy & Mining
Abstract
Research in manipulation of non-metallic particles in a liquid metal by using an electromagnetic (EM) field is promoted by both the requirement of more efficient materials design and the development of cost-effective electromagnetic apparatus. The particles of sub/micrometer sizes can be agglomorated, segregated, aligned and/ or removed by applying a suitable EM field during liquid metal processing. The effciency and applicability depends highly on the nature of the particles and the difference from the liquid metal matrix. In the present paper, the fundaments/physics of non-metallic particles manipulation by EM processing are discussed and some potential application possiblities in industry are proposed.
To improve the efficiency of materials manipulation or obtain a metallic-based materials with required properties has been of broad interest. One of the topics by using an electromagnetic (EM) field concerns the manipulation/removal of non-metallic solid particles in a liquid metal and a variety of related processes using a static electromagnetic field and/or alternating electromagnetic field have been developed [1-4]. Among the processes, a range of electromagnetic effects have been realized which play key roles in determining the engineering of their applications. The physics of these effects are discussed in the following sections by considering different types of EM fields. In order to generate effective electromagnetic effects, the difference in physical/electromagnetic properties between the solid particles and the liquid metal needs to be significant [5,6]. As one of the consequences, the existence of the solid particles will directly influence the physical/chemical properties of the metal after solidification.
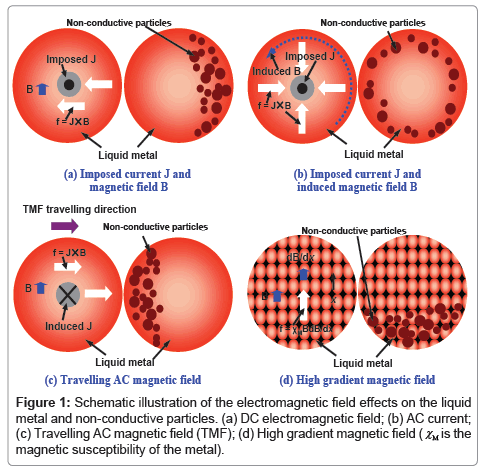
The fundamental of using an electromagnetic field for manipulation is that different electromagnetic forces on the liquid metal and particles can be generated because of the deference in their physical properties [7,8]. In general, four types of electromagnetic fields are usually used: (i) imposing a stationary magnetic field and/or a current; (ii) DC/AC current; (iii) AC magnetic field; and (iv) strong static magnetic field. Figure 1 gives a schematic view of the particle distribution against the liquid metal under different EM fields.
DC/AC Current
An imposed DC/AC current induces a perpendicular magnetic field providing a Lorentz force in a liquid metal. The Lorentz force on the liquid metal is always in the radial direction pointing inwards if a cylindrical conductor is considered (Figure 1). Since the Lorentz force attempts to compress the liquid metal, it is known as the “pinch effect”. When non-conductive particles are present, they will be collected at the wall by this effect [7]. The layer with accumulated particles presents distinct wear properties and graded metallic-based materials can therefore be prepared. In a current density of 4000 kA/ m2, the collection efficiency of 30 μm Al2O3 in liquid aluminum can reach 95% [9], indicating that it is a very efficient approach. However, the Lorentz force is rotational with the square of the current frequency and will generate secondary flows in the melt [9]. In another case, axisymmetric flows may be induced due to the non-uniformity of the radial pinch force when the imposed current is radically non-uniform in the cylindrical conductor. They are important factors to determine the particle distribution.
AC Magnetic Field
A time-varying magnetic field generated in an induction coil can induce eddy currents and subsequently a Lorentz force on a liquid metal. This body force produces internal fluid motion without mechanical contact making “magnetic stirring” a well recognized process. The “skin depth” δ is one of the most important parameters to evaluate the AC magnetic field effects. It can be expressed as [10]
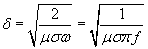 (1)
(1)
where μ the magnetic permeability, σ the electrical conductivity, 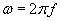 the angular frequency and f is the frequency.
the angular frequency and f is the frequency.
If the magnetic field frequency is low (e.g. 10 Hz), the field can easily pass through the liquid melt because the skin depth (in cm range at 10 Hz) may be larger than the sample thickness. More often, travelling [11,12] or rotating [13] low frequency AC magnetic fields are used in the process of particle removal from liquid metals [14]. As shown in Figure 1 (c), the induced current provides the source for the Lorentz force on liquid metal with the magnetic field. The nonconductive particles are pushed to one side of the cylindrical tube and can be separated.
When the frequency is high (e.g. 10 kHz), the skin depth becomes very small (in mm range at 10 kHz) and may be much lower than the sample thickness. It means that the magnetic field is shielded from the interior of the metal and the induced current exists only in a thin surface layer. A strong stirring effect will be generated in the liquid metal which contributes to improve the homogeneity of the particle distribution and de-agglomerate the cluster of small particles.
Static Magnetic Field with or without a DC/AC Current
A static magnetic field suppresses the liquid metal motion not parallel to the magnetic field lines. This effect is named magnetic damping. When non-conductive particles are present, their migration is also interfered due to the damping in the liquid metal motion. Usually, a combination of a DC magnetic field with a DC current is applied to control the non-conductive particle distribution in liquid metals [15-17]. The DC current is generated between electrodes inserted in the melt [7], while the static magnetic field is applied with permanent magnets or electromagnets. The apparatus can be designed easily. Under the field, the melt experiences electromagnetic forces while a counteractive effect is stimulated on the non-conductive particles due to their nonconductivity [18]. The principle is shown in Figure 1. It has been found that particles of ~100 μm can be efficiently influenced and they can be collected to one side of the liquid metal in a short time [19]. However, it is hardly feasible to scale-up and it remains difficult to manipulate fine particles in the μm range. The generation of a magnetic field higher than 1 Tesla in a large volume remains difficult for conventional electromagnets and keeps the magnet at a temperature below the Curie temperature constitutes a significant technical problem [7].
Strong Static Magnetic Field
With the development of superconducting technology, a magnetic field of 10 Tesla or more becomes easily attainable [20-25]. The advantage of increasing the magnetic flux density is that the magnetic Faraday force in a gradient field as well as the Lorentz with an imposed current can be significantly increased. The particles with a distinct magnetic property experience a different magnetic Faraday force from the liquid metal (Figure 1 (d)).
The magnetic Faraday force is expressed as
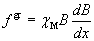 (2)
(2)
where fgr is the magnetic Faraday force, XM the magnetic susceptibility of the metal and B the magnetic flux density.
The Lorentz force is given by
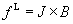 (3)
(3)
where fL is the Lorentz force and J is the current density.
The principle is given in Figure 1 (d) and a difference in magnetic properties (magnetic susceptibility χ) is required in order to manipulate the particles [26]. With the magnetic Faraday force, early research on liquid alloys such as Al-Si alloys evaluated the induced migration and separation [26-28]. The migration time for an alumina particle with a diameter of 20 μm to travel 1 mm was evaluated to be less than 20 seconds under a magnetic field gradient product of around 10 T2/m [26]. However, the force has a comparable magnitude with the gravity force in a high gradient condition for alumina particles (for instance, a gradient product of 600 T2/m) and the manipulation efficiency of micrometer sized particles is very low [5,29].
Therefore, a DC current is usually combined by applying the Lorentz force to manipulate the small particles effectively [29]. The principle is the same as in a traditional DC magnetic field and a current. Detailed investigations have been given in [29] and the non-conductive particles experience the so-called electromagnetic Archimedes forces ( fpEA equation (4)). Alumina particle of 5 μm can be totally collected to one side of the liquid aluminum in 2 seconds in a 40 mm cylinder crucible [29]. The magnitude of the electromagnetic Archimedes force with a 10 T magnetic field and 1500 kA/m2 current can be more than 500 times larger than the magnetic Faraday force [29].
The electromagnetic Archimedes force is obtained as
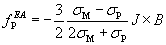 (4)
(4)
where fpEA is the electromagnetic Archimedes force density, σM and σ P the electrical conductivity of the liquid metal and the nonconductive particle respectively.
Energy Efficiency and Benefits of Using a Strong Magnetic Field
When a current is coupled during particle manipulation from a liquid metal, the energy efficiency is another important factor to be considered. In traditional electromagnetic processes, the power is mostly consumed to heat the melt instead of separating the particles [7]. The Joule heating per unit volume is derived from
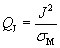 (5)
(5)
The induced driving force fpEA for particle removal can be obtained by equation (4). Therefore, the effective power spent on the particle migration is
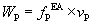 (6)
(6)
where vP is the terminal velocity of a particle.
The terminal velocity is obtained from
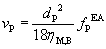 (7)
(7)
where dP is the diameter of the particle, ηM,B is the viscosity of the liquid metal in a magnetic field (calculated in [6]).
By substituting equations (4) to (7), the effective power to promote particle removal is
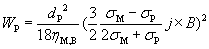 (8)
(8)
The energy coefficient ϕ is defined as the ratio of the effective power WP to the Joule heating QJ , allowing to evaluate the energy efficiency of the process.
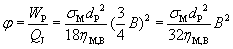 (9)
(9)
The dissipation energy due to the Joule heating is
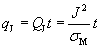 (10)
(10)
where t is the electromagnetic field treatment time.
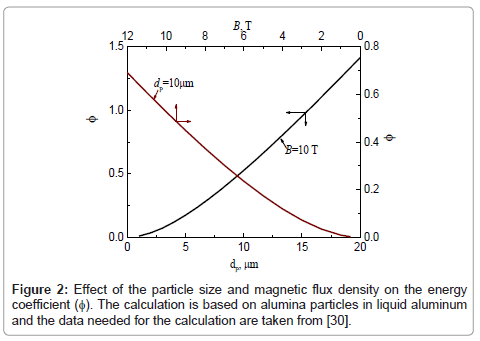
The two factors, magnetic flux density and particle particle size, are further considered. The calculated results are shown in Figure 2, revealing that the energy coefficient increases dramatically with the magnetic flux density. For particle size of 10 μm, the energy coefficient ϕ reaches around 1 which is much higher than in the conventional electromagnetic processes [7,8,30].
Conclusion
The fundamentals of electromagnetic field manipulation nonmetallic particles in a liquid metal are discussed. It is found that two types of electromagnetic forces on the particles, i.e. Lorentz force/ electromagnetic Archimedes force and magnetic Faraday force, are induced during electromagnetic field processing. At high temperatures, both the liquid metal and non-conductive particles are weak magnetic and the magnetic Faraday force is too small to reach an effective manipulation of micrometer sized particles. The Lorentz force can be further combined by applying a DC current. With a sufficiently strong magnetic field and suitable design, the energy coefficient can be highly improved. Therefore, using a strong magnetic field to manipulate micrometer sized particle in a conductive liquid metal is considered to be more promising and effective. However, additional research should be focused on scale-up and the design of industrial systems to meet practical applications.
Acknowledgements
The author acknowledges Prof. B. Blanpain, M. Guo, J. Vleugels and O. Van der Biest from KU Leuven for their suggestions and help. This paper was partially exposed in the magazine of Magnetics Technology International.
References
- Zhang L, Ciftja A, Damoah L (2007) Removal of non-metallic inclusions from molten aluminum. Proceedings of EMC.
- Zhou M, Shu D, Li K, Zhang WY, Ni HJ, et al. (2003) Deep filtration of molten aluminum using ceramic foam filters and ceramic particles with active coatings. Metallurgical and Materials Transactions A 34: 1183-1191.
- Mirgaux O, Ablitzer D, Waz E, Bellot JP (2009) Mathematical Modeling and Computer Simulation of Molten Aluminum Purification by Flotation in Stirred Reactor. Metallurgical and Materials Transactions B 40: 363-375.
- Kang CG, Youn SW (2004) Mechanical properties of particulate reinforced metal matrix composites by electromagnetic and mechanical stirring and reheating process for thixoforming. J Mater Process Technol 147: 10-22.
- Sun Z, Guo M, Kokalj T, Van der Biest O, Blanpain B (2009) Migration and interaction behavior of electrical-insulating particles in a conductive melt under strong magnetic field with high gradient. EPD Congress 785-792.
- Sun Z, Guo M, Verhaeghe F, Vleugels J, Van der Biest O, et al. (2010) Magnetic interaction between two non-magnetic particles migrating in a conductive fluid induced by a strong magnetic field - an analytical approach. Progress in Electromagnetics Research-PIER 103: 1-16.
- Makarov S, Ludwig R, Apelian D (2000) Electromagnetic separation techniques in metal casting. I. Conventional methods. IEEE Trans Magn 36: 2015-2021.
- Makarov S, Ludwig R, Apelian D (2001) Electromagnetic separation techniques in metal casting. II. Separation with superconducting coils. IEEE Trans Magn 37: 1024-1031.
- Zhang BW, Ren ZM, Wu JX (2006) Continuous electromagnetic separation of inclusion from aluminum melt using alternating current. Transactions of Nonferrous Metals Society of China 16: 33-38.
- Sneyd AD (1993) Theory of electromagnetic stirring by AC fields. IMA J Management Math 5: 87-113.
- Noeppel A, Budenkova O, Fautrelle Y (2009) Numerical investigation of the influence of forced convection induced by a travelling magnetic field during solidification of metallic alloys. Magnetohydrodynamics 45: 497-503.
- Yanqing S, Yanjin X, Lei Z, Tiejun Z, Shiping W, et al. (2010) Study on traveling magnetic field casting of sheet components. China Foundry 7: 259-264.
- Nikrityuk PA, Eckert K, Grundmann R (2006) A numerical study of unidirectional solidification of a binary metal alloy under influence of a rotating magnetic field. Int J Heat Mass Transf 49: 1501-1515.
- Asai S (2000) Recent development and prospect of electromagnetic processing of materials. Sci Technol Adv Mater 1: 191.
- Weier T, Gerbeth G, Mutschke G, Lielausis O, Lammers G (2003) Control of Flow Separation Using Electromagnetic Forces. Flow, Turbulence and Combustion 71: 5-17.
- Makarov S, Ludwig R, Apelian D (1999) Electromagnetic visualization technique for non-metallic inclusions in a melt. Meas Sci Technol 10: 1047.
- Olof S, Maurizio V (2007) Use of electromagnetic equipment for slab and thin slab steel continuous caster. Metalurgija 13: 11-20.
- Leenov D, Kolin A (1954) Theory of Electromagnetophoresis. I. Magnetohydrodynamic Forces Experienced by Spherical and Symmetrically Oriented Cylindrical Particles. J Chem Phys 22: 683.
- Yoon EP, Kim JH, Choi JP, Kwon HR (2002) Effects of electromagnetic force on the removal of alumina particles in molten A356 aluminum alloy. J Mater Sci Lett 21: 739-742.
- Herlach F, Miura N (2003) High Magnetic Fields: Science and Technology: World Scientific Publishing Company 2.
- Sun Z, Guo M, Vleugels J, Blanpain B, Van der Biest O (2011) Induced migration of non-magnetic particles and fabrication of metallic-based graded materials by applying a strong magnetic field. J Appl Phys 109.
- Sun Z, Guo M, Vleugels J, Van der Biest O, Blanpain B (2010) Strong magnetic field induced segregation and self-assembly of micrometer sized non-magnetic particles. PIER B 23: 199-214.
- Sun Z, Zhang L, Guo M, Vleugels J, Van der Biest O, et al. (2010) Non-magnetic anisotropic-materials preparation by a strong magnetic field during the solidification of a hypereutectic Al-Cu alloy. EPL 89: 64002.
- Sun Z, Guo M, Vleugels J, Van der Biest O, Blanpain B (2011) Strong magnetic field-induced segregation and alignment of nonmagnetic particles. J Appl Phys 109: 1-3.
- Sun ZH, Zhang X, Guo M, Pandelaers L, Vleugels J, et al. (2012) Strong magnetic field effects on solid-liquid and particle-particle interactions during the processing of a conducting liquid containing non-conducting particles. J Colloid Interface Sci 375: 203-212.
- Asai S (2004) Application of high magnetic fields in inorganic materials processing. Modelling Simul Mater Sci Eng 12.
- Jin F, Ren Z, Ren W, Deng K, Zhong Y, et al. (2008) Effects of a high-gradient magnetic field on the migratory behavior of primary crystal silicon in hypereutectic Al-Si alloy. Sci Technol Adv Mater 9.
- Wang Q, Wang CJ, Liu T, Wang K, He JC (2007) Control of solidified structures in aluminum-silicon alloys by high magnetic fields. J Mater Sci 42: 10000-10006.
- Sun Z, Guo M, Vleugels J, Van Der Biest O, Blanpain B (2009) Numerical calculations on inclusion removal from liquid metals under strong magnetic fields. PIER 98: 359-373.
- Shu D, Li TX, Sun BD, Wang J, Zhou YH (1999) Study of electromagnetic separation of nometallic inclusions from aluminum melt. Metallurgical and Materials Transactions A 30: 2979-2988.
Relevant Topics
- Additive Manufacturing
- Coal Mining
- Colloid Chemistry
- Composite Materials Fabrication
- Compressive Strength
- Extractive Metallurgy
- Fracture Toughness
- Geological Materials
- Hydrometallurgy
- Industrial Engineering
- Materials Chemistry
- Materials Processing and Manufacturing
- Metal Casting Technology
- Metallic Materials
- Metallurgical Engineering
- Metallurgy
- Mineral Processing
- Nanomaterial
- Resource Extraction
- Rock Mechanics
- Surface Mining
Recommended Journals
Article Tools
Article Usage
- Total views: 16480
- [From(publication date):
September-2012 - Apr 21, 2025] - Breakdown by view type
- HTML page views : 11834
- PDF downloads : 4646