Research Article Open Access
Noise Cancellation Using Fuzzy Inference System
Ramanpreet Kaur1*,Simarpreet Kaur2*1Department of Electronics, CEC, Landran, Mohali, Punjab, India
2Department of Electronics, BBSBEC, Fatehgarh Sahib, Punjab, India
- *Corresponding Author:
- Ramanpreet Kaur
Sr. Lect. (ECE Deptt.), CEC, Landran, Mohali, Punjab, India
E-mail: ramnpreet.71@gmail.com - Simarpreet Kaur
Asstt. Professor, (ECE Deptt.), BBSBEC, Fatehgarh Sahib, Punjab, India
E-mail: Simarpreet.kaur@bbsbec.ac.in
Visit for more related articles at International Journal of Advance Innovations, Thoughts & Ideas
Abstract
Noise Cancellation technology is aimed at reducing unwanted ambient noise and can be achieved using two different methods. The first of these is passive noise cancellation which is an approach that focuses on preventing sound waves from reaching the eardrum, and active noise cancellation which uses aural overlap and destructive interference to target and attenuate background noise. While passive and active noise cancellation may be applied separately, they are often combined to attain maximum effectiveness in noise cancellation. In this paper, a noisy signal has been applied as an input to Takagi-Sugeno- Kang (TSK) FIS and a filtered output has been obtained. Using fuzzy rule base and membership functions, if then rules have been created to cancel the noise from noisy signal and surface view has been plotted.
Keywords
Fuzzy Logic, Fuzzy Inference System (FIS), Membership Function, Takagi-Sugeno- Kang (TSK).
Introduction
Noise Cancellation means removal of unwanted signal like removing noise from a noisy signal. Noise Cancellation can be achieved using adaptive filters [4]. A voluminous work is available in noise cancellation using neural networks. There are numerous techniques available using Gradient Search Method [8], Least Square Design [5], Hopfield Network based Design [10], Chebyshev Approximation [6], etc. for noise cancellation. Most of these methods are analytical techniques. They work well with well-defined filter formats and the availability of accurate design data, such as the input and output of the filter. In this paper, an attempt has been made for noise cancellation using fuzzy inference system. A comparison has been shown between Neural Network Approach and Fuzzy Inference System approach in Table 1.
Fuzzy Inference System
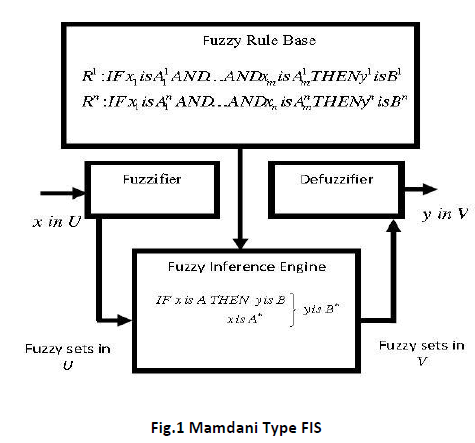
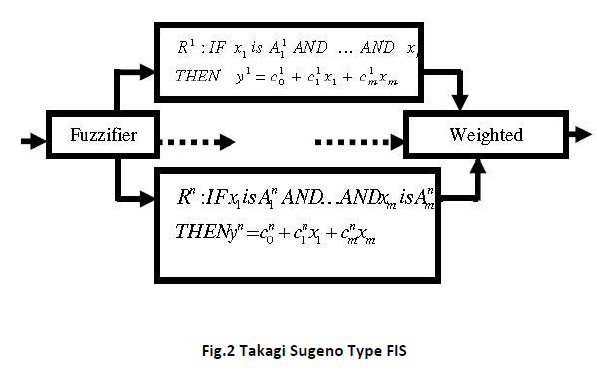
Fuzzy Logic is extension of Boolean logic. It incorporates partial values of truth. Fuzzy logic is a problem-solving control system methodology Fuzzification is generalization of theory from discrete to continuous [1]. It can be implemented in software, hardware, or a combination of both. Fuzzy logic provides a simple way to arrive at a definite conclusion. Conclusion is based upon ambiguous or vague, noisy, imprecise, or missing input information. By using fuzzy logic, designers can realize superior features, lower development costs, optimized and better end product performance. Products can be brought to market faster and also more cost-effectively. Fuzzy logic is gaining increasing acceptance for the past couple of years. Fuzzy logic consists of simple rules-like if X and Y then Z. It does not model system mathematically. Fuzzy logic models are called as Fuzzy Inference System [1,3]. These models consist of number of conditions i.e "ifthen" rules. Fuzzy Inference Systems (FIS) are rulebased systems. It is based on Fuzzy Set Theory and Fuzzy Logic. FIS are mappings from an input space to an output space. FIS allows constructing structures which are used to generate responses (outputs) for certain stimulations (inputs). In terms of inference process, there are two main classes of FIS viz. the Mamdani-type FIS shown in Figure 1 and the Takagi-Sugeno- Kang (TSK) type FIS shown in Figure 2. TSK FIS is also called as Sugeno FIS. In Mamdani based Fuzzy Inference System, inputs and output have an If-Then rules. A typical rule in a Mamdani fuzzy model is : IF X is Negative Big AND Y is Negative Small THEN Z is Very Small. Sugeno-type systems are used to model any inference system in which output membership functions are either linear or constant. It is also called as Takagi-Sugeno-Kang. Sugeno output membership functions, z are either linear or constant. A typical rule in a Sugeno fuzzy model is : If Input 1 = x and Input 2 = y, then Output is z = ax + by + c. For a zero-order Sugeno model, the output level z is a constant (a=b =0). A zero order Sugeno FIS can reasonably approximate a Mamdani FIS. In computational terms, a Sugeno FIS is more efficient than a Mamdani FIS [6,8]. It is so because, Sugeno FIS does not involve computationally expensive defuzzification process. Also, a Sugeno FIS always generates continuous surfaces. The continuity of the output surface is quite important.
Noise Cancellation Using MAMDANI FIS
In this section, we have developed a fuzzy logic based scheme to filter a noisy signal. This can be applied in industrial domain to reduce noise from signal. A one input and one output MAMDANI Fuzzy Inference System is designed for the filter where the input is a noisy signal and the output is a filtered output. Fuzzy rules have been used to obtain the filtered output. The de-fuzzified filter output has been obtained using centroid method. A graph between input and output is also plotted in Figure 3 where filtered output is taken along Y axis and noisy signal is taken along X axis. The membership functions used for noisy signal are: Very small noisy signal, small noisy signal, medium noisy signal, zero noisy signal, large noisy signal and very large noisy signal. The membership functions used for filtered output are: Small filter operation, Medium filter operation, Zero filter operation and large filter operation. The six membership functions used for input are:
MF1='med': 'trimf',[31.3174603174603
43.0174603174603 54.9174603174603]
MF2='small': 'trimf', [14.7611111111111
25.5291005291005 40.3111111111111]
MF3='zero': 'trimf',[48.8222222222222
61.0222222222222 76.3222222222222]
MF4=‘vsmall’: 'trapmf', *0.905550264550259
1.10555026455026 4.36455026455026
20.5026455026455]
MF5='vlarge': 'trapmf',[83.994708994709
94.1 99.1 99.1]
MF6='large': 'trimf',[64.6825396825397 78.8 95.1]
The four membership functions used for output are :
MF1='Med': 'trimf',[0.306 0.438 0.564814814814815]
MF2='Zero': ‘trimf',*0.52189417989418
0.65589417989418 0.80789417989418]
MF3='Large': 'trimf',[0.747354497354497 0.861 1]
MF4='small': 'trimf',[0.00267248677248675
0.183872486772487 0.377772486772487]
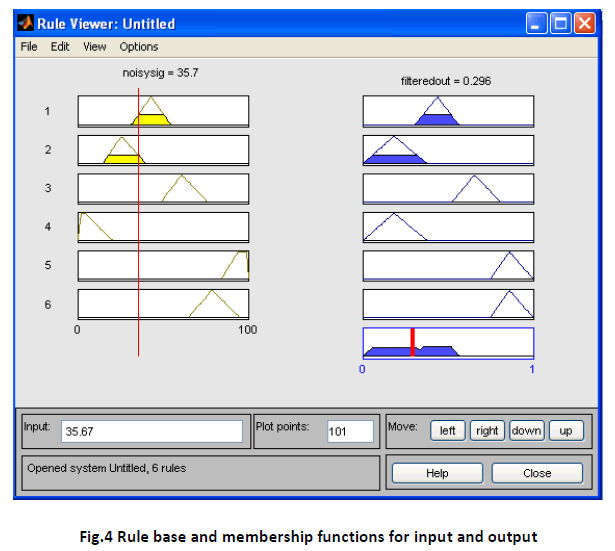
Figure 4 shows the six membership functions used for noisy signal input and the filtered output. As the noisy
signal value increases, the filter output decreases. Since the input noisy signal range has been selected
between 0 to 100 and to view the variation in filtered output as noisy signal vary, the surface view has been
plotted in Figure 3.All the results have been obtained in MATLAB.
Results and Discussion
In this paper, an attempt has been made to design a MAMDANI FIS using fuzzy rule base and membership functions. A comparison between Neural Network approach for noise cancellation and FIS approach is also made. From the previous study, it has been found that the computational complexity and time consumption using neural network approach is much greater than the FIS approach. For a noisy signal in the range 0 to 100, if 35.7 is selected as input we get filtered output of 0.296. Similarly, for different values of the input signal, the value of the filtered output can be measured. In future scope, more than one input can be considered and the response can be viewed using MATLAB. Not only this, but by increasing the membership functions and by using different de-fuzzification methods (other than centroid method used here), the output response can be viewed. Another FIS i.e. Sugeno FIS can also be obtained using fuzzy or some other AI technique like Neuro Fuzzy [2].
References
- Abraham, A. (2001), “It is time to Fuzzify Neural Networks”. Proceedings International Conference on Intelligent Multimedia and Distance Education 2001, Fargo, USA, pp: 253-273.
- Chen, Z., Aghakhani,S., Man, J. and Dick, S. (2011), “ANCFIS: ANeuro Fuzzy Architecture employing Complex Fuzzy Sets”, IEEE Transactions on Fuzzy Systems, Vol 19, no. 2, pp: 305-312.
- Górriz, J.M., Ramírez, J., Alvarez, S.C., Puntonet, C.G., Lang, E.W. and Erdogmus, D., “A Novel LMS Algorithm Applied to Adaptive Noise Cancellation”, IEEE Signal Processing Letters, Vol. 16, No. 1, 2009, pp: 34-37.
- Hadei,S. A. and Lotfizad, M., (2011), A family of “Adaptive Filter Algorithm in Noise Cancellation for Speech Enahnncement”, International journal of Computer and Electrical Engineering, Vol. 2, No. 2, pp: 307-315.
- Kidambi.,S.,” Weighted Least-Squares Design of Recursive All pass Filters”, IEEE Transactions On Signal Processing, Vol. 44, NO. 6, 1996, pp: 1553-1557.
- Parks,T. and McClellan,J., “Chebyshev Approximation for Non-recursive Digital Filters with Linear Phase”, IEEE Transactions On Circuit Theory, Vol. 19,No. 2, 1972, pp: 189-194.
- Russo, F.,“Neuro-Fuzzy Approach to Nonlinear Filtering of Noisy Images”, IEEE Proceedings of Image Proceedings, Vol. 3, 1997, pp: 412-415.
- Widrow. B. and Stearns. S.D., “Adaptive Signal Processing”, Prentice-Hall, 1985.
- Yin, L., Astola, J., and Neuvo, Y., (1991):”Adaptive Neural Filters”, Proceedings of Neural Network for Signal Processing Workshop-1991,pp: 503-512.
- Zhao, H. and Juebang Yu., (1997): “A Novel Neural Network-based Approach for Designing Digital Filters”, IEEE International Symposium on Circuits and Systems 1997,pp: 2272-2275.
Relevant Topics
- Advance Techniques in cancer treatments
- Advanced Techniques in Rehabilitation
- Artificial Intelligence
- Blockchain Technology
- Diabetes care
- Digital Transformation
- Innovations & Tends in Pharma
- Innovations in Diagnosis & Treatment
- Innovations in Immunology
- Innovations in Neuroscience
- Innovations in ophthalmology
- Life Science and Brain research
- Machine Learning
- New inventions & Patents
- Quantum Computing
Recommended Journals
Article Tools
Article Usage
- Total views: 15395
- [From(publication date):
May-2012 - Jul 15, 2025] - Breakdown by view type
- HTML page views : 10685
- PDF downloads : 4710