Modified Bertaut Method to Determine Cation Distribution and Valence State in Powders of Spinels through X-Ray Diffraction
Received: 18-Feb-2023 / Manuscript No. JMSN-23-89622 / Editor assigned: 21-Feb-2023 / PreQC No. JMSN-23-89622(PQ) / Reviewed: 07-Mar-2023 / QC No. JMSN-23-89622 / Revised: 15-Mar-2023 / Manuscript No. JMSN-23-89622(R) / Published Date: 24-Mar-2023
Abstract
In this work a new method is proposed to tackle down the multiple objective optimization problem of the calculation of cation distribution in spinels structure, through the difference of intensity ratios between experimental and calculated intensities of cation sensitive Bragg planes, by introducing a new factor, Rabs, in Bertaut method. This factor is introduced as the sum of absolute R factors, and it is minimized by varying cation distribution. To test this method aluminate manganese spinel where synthesized though modified Pechini method and characterized though XRD. The results show to be in agreement with literature for the aluminum inversion in tetrahedral sites, which is near to the reported value of 10%. Also, it was noticed that the manganese atoms are present in octahedral sites with a mixed valence state of +2 and +3. This might be an indicator that oxygen vacancies are present in the structure, so the vacancies value of oxygen is proposed considering the total charge of cations and thus proposing the value of 3.678 mol per formula unit of the spinel, thus having the next stoichiometry considering normalized Al and Mn, MnAl2O 3.678. Finally, the final cation distribution proposed was [Mn+20.867Al+30.129][Mn+20.034Mn+30.098Al+31.871]O3.678 with a R abs factor value of 0.6466, which considers the cation distribution and oxygen vacancies.
Keywords
XRD; Spinels; Vacancies; Optimization; Cation distribution
Introduction
Spinel structure has as general chemical formula AB2X4. Where A atoms are elements with +2 valence state, B atoms are elements with +3 valence state and X is usually oxygen or a chalcogenide such as sulfur. In last case, spinels are named thiospinels. The order of cations in A and B sites sometimes has an inversion of atoms occupation site. It means in A site (tetrahedral site) +3 valence state atoms and in B site (octahedral site) +2 valence state atoms. Suggesting an inverse spinel [1-4].
Some spinels have an intermediate distribution of cations between A and B site as mixed spinel. It is the most common state for even normal spinels. The ordering of the cations in the spinel structure directly determines the behavior of its optical, electrical, magnetic, thermal, and chemical properties. Thus, it is important to determine the inversion spinel degree [3, 5-7].
Transition metals have usually more than one allowed valence state, such as Mn that can have up to 7 valence states: 0, +1, +2, +3, +4, +5, +6 and +7. Since the valence state also affects the properties of the spinel, it is fundamental to estimate the average valence state when present mixed spinels. By intensity ratios of X-Ray diffraction planes sensitive to cation distribution; which is an easiest and more reliable technique rather than neutron diffraction, Mossbauer spectroscopy or X-Ray photoelectron spectroscopy [8-11].
Recently we have been studying aluminum manganese spinels, for the purpose of using it as a cathode material in aluminum ion batteries. In batteries one aspect that might dictate the electrochemical behavior of the spinel in the electrochemical cell is the cation distribution of the atoms in the structure since a redox couple and the valence of the transition metals tends to change to lower or higher average valence. Then, to study the cation distribution of these spinels we developed a more accurate method to approximate the cation distribution based on the works of Bertaut et al, Ashish and Hiren, Siva Ram Prasad et al. and Lakhani et al. [3,9,12].
Manganese aluminate spinels are a class of materials that have the chemical and structural formula AB2O4, thus crystallize in the same structure as MgAl2O4. It holds the space group No 227 FD3-Mwith Mn atom occupying A site with a valence of +2 and Al atoms occupying B site with a valence of +3. (See Figure 1 Supplementary Information) Although this spinel is pointed out to be a normal spinel it tends to show a small degree of inversion as pointed by Stokes et al, with a value of inversion of i=0.1, where also it has been found that the Mn atoms in B site have +2 and +3 valence states showing an average valence state higher than expected and that depends on the method of synthesis. [9, 13]
The atomic coordinates for this spinel vary depending on the origin choice for the space group FD3-M . Two different equipoints with point symmetries 4-3m and 3-m are possible origins for the unit cell. Thus, having the next Wyckoff positions for the atoms for each origin setpoint, see Table 1 [14].
| Origin Choice | Wyckoff Positions | ||
|---|---|---|---|
| Al | Mn | O | |
| 1 | 8a | 16b | 32e |
| 2 | 8b | 16c | 32e |
Table 1: Wyckoff positions of atoms for the two possible origin choice for space group 227.
Considering the multiple valence state that manganese can have, it has been pointed out by Stokes et al that the general cation distribution formula for this spinel could be [Mn+21-(i+x)Al+3i][Mn+2iMn+3xAl+31-i]O4 [9].
Methodology
Synthesis of Manganese Aluminate Spinels
The synthesis was performed by the modified Pechini method which involves making a solution in a beaker with deionized water and the metal chloride salts of Al and Mn in stoichiometric quantity according to target stoichiometry. To this solution was added pure ethylene glycol and was stirred under heat to 50°C for 20 min. Citric acid was added as complexing agent in molar relation to salts of 3:1 and the solution was heated to 150°C for 5 hrs. for poly-esterification reaction. After gelation this was taken to an oven at 200°C for 3 hrs to dry the gel. Following a calcination step at 1100°C for 2 hours with a heating curve of 20°C/min [15-17]
X-Ray diffraction intensity
For the determination of cation distribution, it is considered the ratios of the intensity between sensitive planes to cation distribution such as (220), (400), (422) and (440). (220) and (422) planes are sensitive to cation distribution in A site, while (400) and (440) planes are sensitive to both A and B site cation distribution, as evidenced Vara Prasad et al. The reason to consider ratios of planes intensity rather than individual intensities is because ratios of intensity allow to avoid crystal preferential orientations in powder samples. [1]
The most important value to determinate the intensity planes ratios, is the relative intensity for each individual plane, thus the formula for calculating the intensity of diffraction for a determined plane can be expressed as equation 1. [18]

Where, Ihklis the relative integrated intensity, Fhklis the structure factor,P is the multiplicity factor (see table 3) and Lp is the Lorentz polarization factor (see equation 7)
Structure Factor
The structure factor is calculated considering the atomic scattering factor. The atomic scattering factor is used to describe the efficiency of scattering of the atoms in a given direction, so it is defined as a ratio of amplitudes, see equation 2.
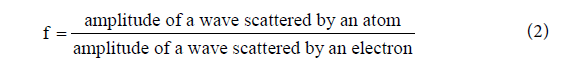
Atomic scattering factor depends on the Bragg angle and the wavelength of incident beam. The calculation of f involves sinθ rather than the value of θ , due to the net effect is that f decreases as quantity increases. The scattering factor f is sometimes called the form factor because it depends on the way in which of electrons are distributed around the nucleus at the atom. The resultant wave scattered by all atoms in the unit cell is called the structure factor because it describes how the atom arrangement affects the scattered beam. Thus, the structure factor, designated by the symbol F, is obtained by simply adding together all the waves scattered by individual atoms. If a unit cell contains atoms 1, 2, 3…N, with fractional coordinates u1 v1 w1, u2 v2 w2, u3 v3 w3… and atomic scattering factors f1, f2, f3…, then the structure factor for a hkl reflection is given by equation 3, [12, 15, 18]

Then, the structure factors equations for the Bragg planes, as stated
by Ashish and Hiren, in the spinel structure are the ones shown in Table 2. [12]
| Bragg´s Planes | Structure Factor |
|---|---|
| -220 | -8FA |
| -311 | 4(−√2FA−2FB) |
| -400 | 8(-FA+2FB+4FO) |
| -422 | 8FA |
| -440 | 8(FA+2FB+4FO) |
Table 2: Structure factors for special Bragg planes of spinel structure.
Where, FA and FB are structure factors for A site and B site cations and FO oxygen.
The atomic form factor for each atom in each plane, which is employed in the determination of the structure factor of a Bragg plane; is determined as the atomic form factor multiplied by the occupation in the site by the atom and the adding this factor for each atom present in the site. The atomic form factor is the Fourier transforms of the electron density of an atom; it is assumed a spherically symmetric electron density, its values of the Fourier transform only depend on the distance from the origin of the reciprocal space. It is approximated by a sum of Gaussians. (See equation 4)
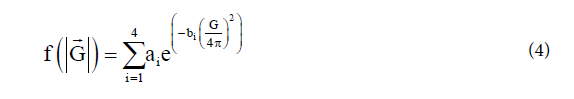
Where vector equals and the sum can be computed for
factors ai, bi and c from coefficients computed by Mann and Cromer. (See supplementary information Table 1) [19]
Multiplicity Factor (p)
The relative proportion of planes that contribute to the same reflection enters the intensity equation as the magnitude p may be defined as the number of different planes in a form having the same spacing. The value of p as a function of hkl are given below in table 3 [18]
| Bragg´s Planes | Multiplicity Factors |
|---|---|
| -220 | 12 |
| -311 | 24 |
| -400 | 6 |
| -422 | 24 |
| -440 | 24 |
Table 3: Multiplicity factors for special Bragg planes for spinel structure.
Lorentz Polarization Factor (Lp)
To considerate trigonometrical factors that influence the intensity of the reflected beam. It is calculated a polarization and Lorentz corrections to remove its effect from the relative intensity of Bragg peaks and background. (See equations 5 and 6)

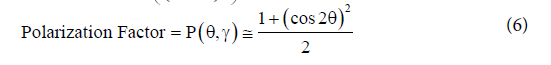
Then, both equations get combined to obtain a single Lorentz- Polarization factor that is expressed as shown in equation 7 [18]
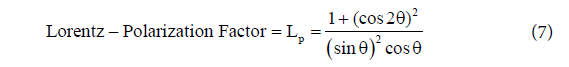
Method
Usually when the method of intensity ratios for sensible planes to cation distribution is employed; a mapping of the concentration of cations in each side is done, where a changes in cation normal to be at B site is done by 5% step down to a 50% changes in concentration at A site. Then the cation distribution that gives the closest value to 0 for each R factor for each intensity ratios between experimental and calculated is looked minimal for the four ratios [1-3, 12]. The problem with it is the time consumed looking for the lowest R factor for the four ratios, and another problem is that by considering more elements and valence states in the system the permutations increase exponentially making more difficult to analyze the cation distribution of the system.
Since, the nature of this problem is a multiple objective optimization; we proposed a new factor Rabs which is the sum of all absolute R factors of each difference of intensity ratios between experimental and calculated intensities. (See equation 8)

Where,




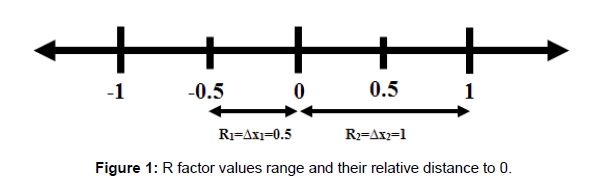
The reason to take the absolute value of the equations 9,10, 11 and 12 is the fact that sometimes with some cation distributions the difference will have some values that are negative but may be also a minimum. So, to take the closest value of R to 0 we have to consider only the distance from 0 no matter if it is positive or negative; then making sure that we have the global minima and not a local minimum. For example, if we consider a value of R1=-0.5 and R2=1; the value that is closest to 0 is -0.5 (See figure 1).
Thus, by employing this new equation we can make this multiple objective optimization problem a single objective optimization, where we want to optimize Rabs to 0; which would be when no difference is present between ratios.
The solution for this single objective optimization was tackled down with the algorithm Evolutionary Solver. In which a minimization target was set, and the next constraints were set Al+3 B site ≤2, Al+3 B site >=1, Mn+2 B site<=1,Mn+2B site B site >=0, Occupancy of B site should be 2.
1. Characterization XRD
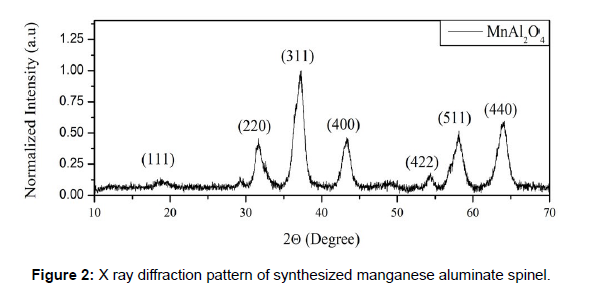
The X-Ray diffraction patterns were acquired in an X´pert Pro analytical system with a Cu Κα X-Ray source with a wavelength of 1.541 Å, with a 2Θ range from 10° up to 70° with a step of 0.016 at 298.19 K under air.
2. Iobs/Ical Method
The proposed method was applied to manganese aluminate spinels and the next 2Θ and intensity for the Bragg planes were acquired through the experimental XRD characterization of the spinel. (See table 4)
Bragg Planes |
2Θ(°) |
|---|---|
| -220 | 31.64 |
| -311 | 37.32 |
| -400 | 43.43 |
| -422 | 54.46 |
| -440 | 64.02 |
Table 4: 2Θ position and relative intensity of Bragg planes.
The X-Ray diffraction pattern was normalized to highest intensity Bragg plane (311). (See figure 2).
Average valence state
The average valence state of the transition metal in the structure of the spinel was calculated by adding the concentration of +2 valence in both sites A and B site and the same procedure for +3 valence. Then it was multiplied by the concentration of each valence on both sites.
Results
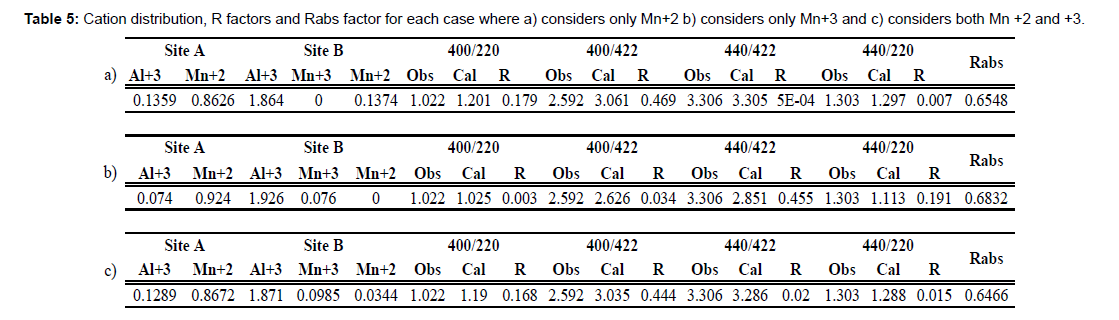
The method described before are shown in table 5. Where three cases were optimized in order to determine the valence state of the cations in the spinel structure of manganese aluminate spinel. Since Stokes et al. have made the statement that this spinel shows two valence states for the occupation of Mn in B site, which is with valences +2 and +3. So, to test the method an optimization was calculated where only Mn+2 was considered in B site, which is shown in the first 3 rows of table 5. It can be pointed out that it has agreement between R factors due to the individual R factor is less than 1, Rabs=0.6548. Also, can be pointed out that an inversion is shown where aluminum is present in A site in an occupancy of 0.136, which is in really agreement to the reported by Stokes et al and Pierre Villars [19, 20].
The second case tested where only Mn+3 was allowed to be in B site, is shown in table 5 rows 4 to 6. In the value of Rabs has increased its values to 0.6832 suggesting that even though +3 is the valence of the site B, it means some manganese +2 might be in the site since the Mn+2 only allowed case showed a smaller Rabs value than this case.
Finally, the third case where a mixed valence between Mn+2 and Mn+3 is taking in account and as expected it showed the lowest value of Rabs. This inversion degree for aluminum is near to reported values of 10% in A site. Also, the preference of manganese for A site although it can also be present in B site with a mixed valence, but preferably with the valence of +3 since it is the valence of the site. It has the highest occupancy of manganese in the site B. The still difference between observed/experimental and calculated, meaning the R factors are attributed to the fact that no absorption and Debye-Weller temperature factor were taken in account for the calculation. Since it has been shown that the effect of these factors is small against the cation distribution [1]
The final cation distribution proposed for this sample is the one shown below.
[Mn+20.867Al+30.129][Mn+20.034Mn+30.098Al+31.871]O4
The analysis of the total charge of the cations in the structure, it has a value of positive 7.356; in the ideal structure the oxygen should be 4 atoms per formula unit, meaning a negative charge of -8. Thus, since the electric charge of the structure must be equals to oxygen the difference can be explained as a deficiency in oxygen meaning the structure might have vacancies of oxygen, thus the final proposed cation distribution considering oxygen vacancies as shown below.
[Mn+20.867Al+30.129][Mn+20.034Mn+30.098Al+31.871]O3.678
Now that a final cation distribution is achieved, the total charge of manganese can be calculated and that would be the average valence of manganese which is an important value for applications such as batteries, where it is important to know the average valence of an atom that works in the redox couple of the battery. The average valence of the manganese in this structure is 2.098.
Conclusion
Aluminum manganese spinel was synthetized through the modified Pechini method. Cation distribution was estimated though comparing experimental and calculated X-Ray diffraction intensity ratios of cation sensitive Bragg planes. Afterwards, the average valence of manganese in the structure was calculated. The proposed cation distribution showed an inversion of 12.9% in tetrahedral site for aluminum. Also, the manganese showed to be presents in the octahedral sites and being present in two valence states +2 and +3, which suggests an indication that some oxygen deficiency in the structure is presents. This vacancy was calculated resulting 3.678 mol instead of 4 mol of oxygen per formula unit. These results prove that this method is a robust powerful tool to determine of cation distribution in spinels accurately and with mixed valence in its cations. Achieving similar results for this system as found in literature. In future the absorbance and Debye-Weller factor will be introduced in the method to reduce the Rabs value.
References
- Vara B Prasad, Rajesh Babu B, Siva Ram Prasad M (2015) Structural and dielectric studies of Mg 2+ substituted Ni-Zn ferrite. Mater Sci 33: 806-815.
- Siva Ram Prasad M, Prasad BBVSV, Rajesh B, Rao KH, Ramesh KV(2011) Magnetic properties and DC electrical resistivity studies on cadmium substituted nickel–zinc ferrite system. J Magn Magn Mater 323: 2115-2121.
- Lakhani VK, Pathak TK, Vasoya NH, Modi KB (2011) Structural parameters and X-ray Debye temperature determination study on copper-ferrite-aluminates. Solid State Sci 13: 539-547.
- Tsurkan V, Krug von Nidda HA, Deisenhofer J, Lunkenheimer P, Loidl A (2021) On the complexity of spinels: Magnetic, electronic, and polar ground states. Phys Rep 926: 1-86.
- Islam MA, et al. (2022) Structural characteristics, cation distribution, and elastic properties of Cr3+ substituted stoichiometric and non-stoichiometric cobalt ferrites. RSC Adv 12: 8502.
- Cornu L, Duttine M, Gaudon M, Jubera V (2014) Luminescence switch of Mn-Doped ZnAl2O4 powder with temperature. J Mater Chem C 2: 9512-9522.
- Rana MU, Misbah-Ul-Islam, Abbas T (1999) Cation distribution in Cu-substituted manganese ferrites. Mater Lett 41: 52-56.
- Yuan D, Zhao J, Manalastas W, Kumar S, Srinivasan M (2020) Emerging rechargeable aqueous aluminum ion battery: Status, challenges, and outlooks. Nano Mater Sci 2: 248-263.
- Stokes TN, Bromiley GD, Gatta GD, Rotiroti N, Potts NJ, et al. (2018) Cation distribution and valence in synthetic Al–Mn–O and Fe–Mn–O spinels under varying conditions. Mineral Mag 82: 975-992.
- Bekheet MF, Schlicker L, Doran A, Siemensmeyer K, Gurlo A (2018) Ferrimagnetism in manganese-rich gallium and aluminium spinels due to mixed valence Mn2+–Mn3+ states. Dalt Trans 47: 2727-2738.
- Grosvenor P, Bellhouse EM, Korinek A, Bugnet M, Mcdermid JR. XPS and EELS Characterization of Mn2SiO4, MnSiO3 and MnAl2O4.
- Tanna R, Joshi HH (2013) Computer Aided X-Ray Diffraction Intensity Analysis for Spinels: Hands-On Computing Experience. Int J Phys Math Sci 7: 334-341.
- Wang S, Wei X, Gao H, Wei Y (2019) Effect of amorphous alumina and α-alumina on optical, color, fluorescence properties and photocatalytic activity of the MnAl2O4 spinel oxides. Optik (Stuttg) 185: 301-310.
- Furuhashi H, Inagaki M, Naka S (1973) Determination of cation distribution in spinels by X-ray diffraction method. J Inorg Nucl Chem. 35: 3009-3014.
- Edrissi M, Soleymani M, Naderi M (212) Synthesis of MnAl2O4 nanocrystallites by Pechini and sequential homogenous precipitation methods: Characterization, product comparison, photocatalytic effect, and Taguchi optimization. J Sol-Gel Sci Technol 64: 485-492.
- Shafiekhani, Saeidfirozeh H (2013) Influence of Fe@MnAl2O4 and synthesis of novel compound Mn0.83Fe0.21Al1.96O4. Phys B Phys Condens Matter 421: 122-126.
- Sunde TOL, Grande T, Einarsrud MA (2016)Modified Pechini Synthesis of Oxide Powders and Thin Films. Handb Sol-Gel Sci Technol 1-30.
- Bernard D, Cullity (1978)Elements of x-ray diffraction 555.
- Cromer T, Mann JB (1968) X-ray scattering factors computed from numerical Hartree-Fock wave functions. Urn 24: 321-324.
- Villars P (2016) MnAl2O4 Crystal Structure. SpringerMaterials.
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Citation: Mani-González PG, Cruz JAH (2023) Modified Bertaut Method toDetermine Cation Distribution and Valence State in Powders of Spinels throughX-Ray Diffraction. J Mater Sci Nanomater 7: 065.
Copyright: © 2023 Mani-González PG, et al. This is an open-access articledistributed under the terms of the Creative Commons Attribution License, whichpermits unrestricted use, distribution, and reproduction in any medium, providedthe original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Usage
- Total views: 3978
- [From(publication date): 0-2023 - Nov 14, 2025]
- Breakdown by view type
- HTML page views: 3461
- PDF downloads: 517