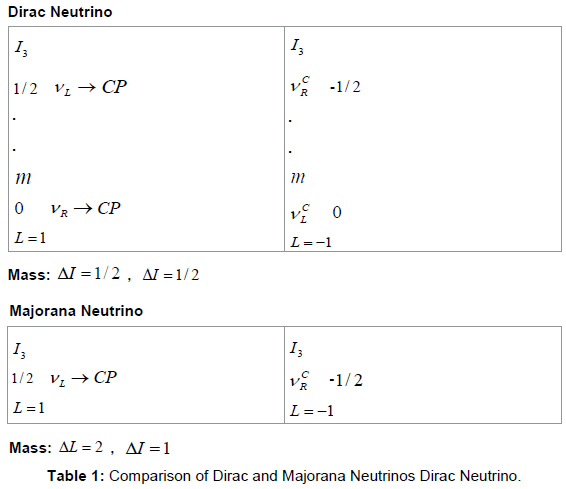Innovative Energy & Research
Open Access

Within the standard model three separate lepton numbers or flavors are conserved, L_e, L_μ, and L_τ Because these conservation laws are not associated with a gauge symmetry as is the case of charge conservation, the violation of lepton number occurs in many extensions of the standard model. The search for lepton number violation is, therefore, an important method for exploring the world beyond the Weinberg-Salam model.

Neutrino mass and lepton number violation are related in two different ways.

1. One may ask why individual lepton numbers are conserved in the standard model-whereas hadron flavors are not as a result of Cabibbo mixing. The answer, of course, is that Cabibbo mixing is unobservable in the lepton sector as long as the neutrinos are degenerate, which is the case if they are all massless. In the standard model all fermions except neutrinos acquire a mass m_D (Dirac mass) by the coupling of the left-handed fermion (e_L, μ_L...) to the right handed singlet fermion (e_R, μ_R...) Neutrinos do not acquire such a mass because the right-handed neutrino is simply omitted from the original cast of characters. A trivial extension of the standard model is obtained by adding single right-handed neutrinos v_eR, v_μR….) and standard model is obtained by adding single right-handed neutrinos v_eR, v_μR….) and giving them a Dirac mass. We then expect there will be Cabibbo like mixing in the lepton sector. If this is the only source of lepton flavor violation all effects of lepton flavor violation are proportional to neutrino mass differences, so that the only observable effect for practical purposes is neutrino oscillation. This model of neutrino mass is not very popular because it uses the same mechanism for neutrino mass as for the mass of other fermions and thus provides no rationale for the relatively very small values of neutrino mass.

2. There is an alternate method for providing neutrino mass, the Majorana mass term which connects v₂ to its right-handed antiparticle v^C_R. Even if there is no v_R in the theory, v^C_R necessarily exists by CP or CPT invariance. While such a term is forbidden by charge conservation for the other fermions it is forbidden for neutrinos only by the conservation of L. Thus the existence of an interaction beyond the standard model that violates L will allow a non-zero neutrino mass. The weakness of this new interaction then may explain the small magnitude of neutrino masses.

The Dirac and Majorana mass terms are compared in Table 1.

Table 1: Comparison of Dirac and Majorana Neutrinos Dirac Neutrino.

In a CP-invariant theory, the Majorana neutrino is a CP eigen state, whereas for a Dirac neutrino the CP transformation changes the neutrino to a different particle, the anti-neutrino. The Dirac mass term involves ΔI = 1/2 where I is the weak isospin whereas the Majorana mass term involves ΔI =1. If weak isospin is broken only by a Higgs doublet with a vacuum expectation value (vev) equal to v₂, then,

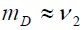
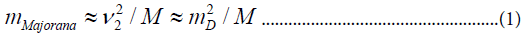
In eqn. 1 we have inserted M for dimensional reasons; [1] in a model M will be associated with the mass scale at which L is broken. All the practical experiments bearing on neutrino mass do not distinguish between Majorana and Dirac neutrinos. Thus the main method of identifying the Majorana mass is a search for ΔI = 2 in other processes such as neutrinoless double beta-decay (ββ)_0ν . While such processes may be mediated in other ways than the exchange of a Majorana neutrino, the violation of lepton number of the form ΔI = 2 necessarily yields a Majorana mass term [2]. We now turn to the question of what motivation exists for introducing a Majorana mass term. The main motivation comes from models, such as SO (10), that possess a quark-lepton symmetry and leftright symmetry so that V_L has a right-handed partner N_R, These models face the problem of why the neutrino mass is not of the same order as the mass of other fermions. The answer due to Gell-Mann, Ramond, and Slansky [3] (GRS) is that N_R (which is a singlet under the usual SU (2) × U (1)) acquires a large Majorana mass M_D that violates L by two units; then the Dirac mass term M_D only mixes V_L with N_R with a probability (M_D/M_N) so that,

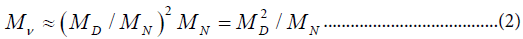
Eqn. (2) was the original form in which the generic equation (1a) arose. One may ask whether it is absolutely necessary to have massive neutrinos in the SO(10) model. The answer is that a modest extension [4] involving adding an SO(10) singlet neutral fermion to each generation allows for a solution with massless neutrinos plus a very massive Dirac neutral lepton for each generation. A further extensions [5] in which two one neutral fermions are added to each generation allows for a solution in which each generation possesses a light Dirac neutrino plus the very heavy Dirac particle [6].

The violation of L_e, L_μ, L_τ with the conservation of L can take place in the absence of neutrino mass as a result of flavor-changing neutral currents. Indeed, considerable effort has been required when different models were developed to avoid such currents. Thus in the gauge sector we have the GIM mechanism while in the Higgs sector we have the proportionality of the coupling to the mass. As soon as we go beyond a single Higgs doublet we get such flavor-changing neutral currents unless some discrete symmetry is imposed. Examples are the effective Higgses of technicolour theories and the two lefthanded doublets in the SU(2)_L × SU(2)_R × U(1) model; Attempts to understand the generation problem such as the gauging of horizontal symmetries often lead to flavor-changing neutral currents.

Leptoquark bosons [7] exist in models that unite quarks and leptons such as the SU(4)_c of Pati and Salam; even if proton decay is forbidden in such models the leptoquark boson masses and couplings are constrained by flavor-changing processes.

Two of the most useful semi-leptonic processes are the coherent (μ_e) conversion in nuclei,

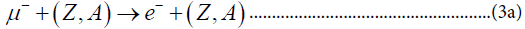
And the decay,

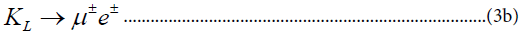
The limits on these processes have been frequently used to constrain models [8]. In many models (such as Higgs exchange) the ΔS = 2K⁰ − K⁰ →μ^± e^± mixing provides a stronger constraint, but, of course, this is not the case for leptoquarks. In the case of (3b) it is possible to imagine that flavor is transferred from quarks to leptons rather than flavor being changed. The purely leptonic processes that have been studied most are:

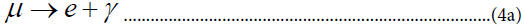
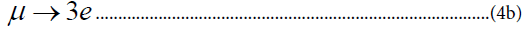
Recently the limit on the μ →3e branching ratio [9] has been reduced to 1.6 × 10^-10 Heavy neutral leptons [10] may play an important role in and some models are constrained by the limits on (4a). The decay (4b) could be mediated by doubly charged bosons that exist in the SU(2)_L × SU(2)_R × U(1) model.

There are several-methods for introducing the violation of total lepton number L into models. There are three general mechanisms:

(E) Lepton number can be explicitly violated in the Lagrangian. This can be done either by a Majorana mass term or by a term in the Higgs potential.

(H) Lepton number can be a gauged symmetry of the Lagrangian, which is then spontaneously, violated. The resulting Goldstone boson is then eaten up by the Higgs mechanism.

(M) Lepton number may be a global ungauged symmetry which is spontaneously broken. As a result, there is a real massless Goldstone boson in the theory. Because this is associated with the generation of a Majorana mass term, the Goldstone boson has been christened a Majoron.

We first look at models which contain right-handed partners N_R for the left-handed neutrinos υL In such models a Higgs boson S which is a singlet under the usual SU(2)_L may be introduced which has a Yukawa interaction of the form,

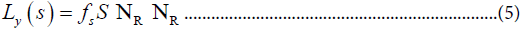
S may be considered as having L=2 so that (4a) conserves lepton number. When S obtains a vev<S>the N_R acquires a Majorana mass. The light neutrino then acquires the mass (2) by the GRS mechanism. We consider two cases:

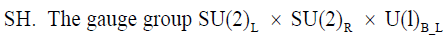
includes B-L as a gauged quantity. In the version of interest to us the Higgs particles consist of ɸ which transforms as (2,2) and plays the role of the usual Higgs doublet and Δ_L, Δ_R which transform as (3,1) and (1,3), respectively. The neutral member of the Higgs boson multiplet SU(2)_R which is a triplet under SU(2)_R but a singlet under SU(2)_L plays a role of S. When it acquires a vev<S>spontaneously, the group is broken down to the usual SU(2)_L × U(l)_y The lepton number is no longer conserved, (although the remains a gauged U (1), essentially the charge 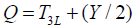; the associated Goldstone boson becomes the longitudinal component of W_R. This model has been discussed in many papers [11] with the idea that the breaking scale M(WR) ≈<S> might be Low enough to yield a variety of observable consequences. A limit 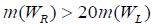exists on the basis of the contribution of W_R to the box diagram [12] contributing to m(K_s)-m(K_L). The use of this model to provide CP violation [13] in K⁰ decay requires m(W_R) ~ 15 TeV. Such a low value for M in eqn. (2) leads to a value of m(v_τ) much greater, than the cosmological limit for stable neutrinos; we discuss this problem later. SM. The gauge group is the usual 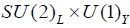but lepton number conservation occurs as the result of a global U(l). When S obtains the vev<S>, the lepton number is broken and 1 m S becomes the massless Majorona [13]. It is natural in this model to have<S>very large so that the coupling f_s can be very small; in this case there are no phenomenological or cosmological consequences beyond the non-zero value of neutrino mass.

We now turn to models in which there is no N_R. In such models there is less motivation for lepton number non-conservation and neutrino mass, but it is still possible. In place of S we need a Higgs T, which is the neutral member of a triplet under the usual SU(2)_L The corresponding Yukawa interaction as far as V_L is concerned is:

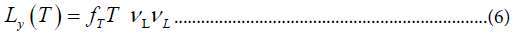
With T having L=2 When T acquires a vev<T>the light neutrino acquires a mass f_T<T>. The value of<T>must be at least an order of magnitude less than v₂ in order that ρ (as measured in the ratio of neutral currents to charged currents) be close to unity. We again consider two cases:

TM. Lepton number conservation is a global U(l) symmetry of the Lagrangian. As a result of spontaneous symmetry breaking T obtains a vev and Im T becomes the massless Majorona [14,15]. Because of the non-trivial behavior of T under SU(2)_L this model has a host of possible consequences for experiments and for cosmology [16] In order to avoid too rapid an emission of Majorons from the cores of red giants (due to doublet-triplet. Higgs mixing which couples T to electrons) (T) must be less than 100 KeV. In order to avoid the bremsstrahlung of Majorons from outgoing neutrinos in K decays f_T (for v_e and v_μ) must be less than 10^-2~10^-3. The most important cosmological consequence of this model is that there is a large cross section for ν +ν →majoron + majoron via neutrino exchange. For 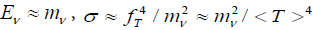Given the upper bound on <T>one finds (for m_e>1 eV) that as the cosmological temperature goes through the value m_v the massive neutrinos annihilate leaving a background of massless Majorons.

TE. Lepton number is violated explicitly in the Higgs Lagrangian by a term:

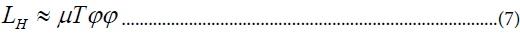
Where μ is a coupling constant with dimensions of mass. In general in this case T may have a sizeable mass M_T and the vev<T>is induced via the interaction (5) as a result of the vev<ɸ>=v2 so that

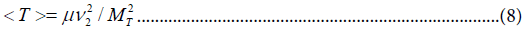
The expression for mv then reduces to the canonical form (l) provided we set:

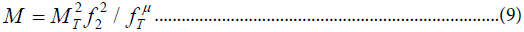
Where f₂ is the usual Yukawa coupling to the doublet Higgs. We discuss later the possibility that is very small so that MT is very small so that effectively the Majorana acquires a small mass. The four models are compared in Table 2.

SH	Gauge group	Higgs interaction	Fate of Higgs	M
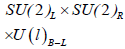		SNR NR	Unphysical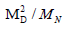
SM		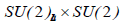SNR NR	Goldstone B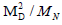
TM		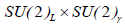	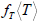Goldstone B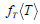
TE		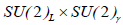	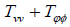Heavy Boson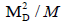

Table 2: Methods of violating total lepton number L.

We now consider the experimental determination of the 3 × 3 Majorana neutrino mass matrix. Even if there exist heavy neutrinos derived from NR we can consider to a good approximation an effective matrix for the three light neutrinos corresponding to the matrix generalization [17] of (2)

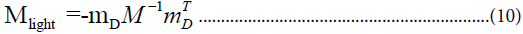
This matrix is specified by three mass eigenvalues mi and three mixing angles U_ij specifying the orthogonal matrix relating 1 the mass eigenstates to the flavor eigenstates. In addition, assuming CP invariance, there are the two relative CP eigenvalues (η12, η13=± 1), which have significant phenomenological consequences. Five types of experiments have been discussed at this conference:

1. Neutrino oscillation experiments provide correlated constraints between squared mass differences (m_i²-m_j²) and mixing angles. For sizeable mass differences the mixing angles must be small.

2. Studies of decay spectra near end points (as in tritium decay) provide a limit on (or a value for) the value mi of the mass eigenstate which dominates a particular flavor state. For all cases of interest mixing effects can be ignored because of the limits placed on mixing angles by neutrino oscillation experiments. For example, in the tritium beta-decay experiment unless there are two mass eigenstates degenerate within 10-3 eV any mixing is limited by the reactor experiments to less than 3% in probability.

In most models the exchange of massive Majorana neutrinos provides the only mechanism for producing an observable rate for the (ββ)_0ν nuclear decay,

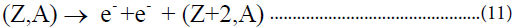
The decay is proportional to the weighted sum,

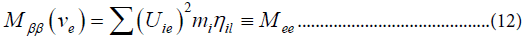
Where, M_ee is the diagonal element of the neutrino mass matrix which connects v_eL and v^C_eR. Thus (ββ)_0ν does not directly provide a limit on the mass of v_e as measured in ³H decay. A small admixture of a heavier neutrino with the opposite CP eigenvalue can cancel in eqn. (11) the large admixture of a light neutrino. Such a cancellation is not necessarily unnatural since as indicated in eqn. (6) the sum has the significance of a single element of the mass matrix.

A small admixture of a heavy neutrino particularly in the range well above 1 MeV can be detected or limited by studying the decay spectrum in π →l + X or K →l + X where l=e or μ.

For still larger masses limits on the mixing may be obtained by attempts to detect the decays induced by the mixing. To the extent that v_τ can be obtained from a beam dump strong limits on (U3e)² can be derived from the search for .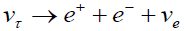

A possible pattern of masses and mixings that seems of interest to me is based on the following assumptions:

Assume neutrino masses follow the generational pattern of other fermions so that 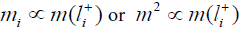. This is expected in models like SO (10) from eqn. (2b).

Assume mixing angles are fairly small as is the case for quarks and that ν_e −ν_τ mixing is negligible.

The heaviest of the three neutrinos has a mass of 10 to 100 eV and corresponds essentially to ν_τ . (This means for the moment we ignore the ³H experiment). The first two assumptions are suggested by many models. The third is the largest mass allowed by cosmology if neutrinos are stable and at the same time is large enough to have interesting cosmological consequences. We then have the pattern,

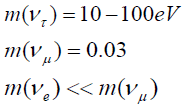
For such a pattern neutrino oscillations are the only relevant experiment. For oscillations of the form 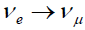or 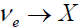, the characteristic 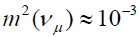to 10 eV [2]. The result reported here from the Bugey reactor with Δm² ~ 0.2 eV² lies in the center of this range corresponding to 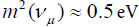. The corresponding mixing angle found is of the order or the Cabibbo mixing between the first two generations. This scenario then suggests that 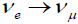oscillations will be characterized by 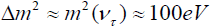. For such large values of Δm² the E53l experiment at FNAL gives a limit of θ² < 3×10⁻³ . It is amusing and conceivably relevant to note that for quarks the mixing of second and third generations is measured by 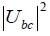≈ 2 to 3× 10^-3. From this point of view it is very worthwhile to push 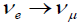oscillation experiments to smaller mixing angles.

Neutrinos above 100 eV: Use Them, and then Lose Them

There are several reasons for interest in neutrino masses well above 100 eV.

(1) If m(V_e) is around 30 eV and neutrino masses scale as those of quarks and leptons, m(V_μ) and will be in the KeV or MeV range.

(2) If the general form of eqn. (l) is accepted and if the heavy mass M should be in an interesting range of around 10 Tev (as needed for example, in the SU(2)_L × SU(2)_R × U(l) model of CP violation [13] one expects m(V_e) to be an the KeV range and m(V_τ) in the MeV range.

(3) Neutrino masses greater than 100 eV can be of interest for galaxy formation.

As is well-known the big-bang cosmology requires that such neutrinos decay or annihilate. Furthermore, there are upper limits on the lifetime depending on the mass and decay products.

(1) For masses (of V_τ) above 1 MeV the most reasonable decay mode is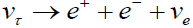

As a result of mixing of V_τ with or V_e. A variety of cosmological arguments corresponding life time; recently Sarkar and Cooper [18] have claimed on the basis of ₄He and D abundance that the lifetime must be less than 10² sec for m(ν_τ) 5 > MeV. The TRIUMF limits on

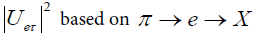
Then require,

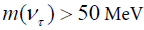. In the range above 50 MeV direct searches for decaying Vτ could rule out such short lifetimes.

(2) For masses below 1 MeV (either V_τ or V_μ below 500 KeV) the conventional decay modes are:

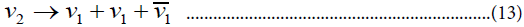
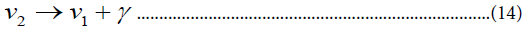
For (12) in order that the energy-density of the product v₁ not to be too large it is required that:

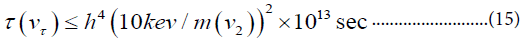
Where, the Hubble constant is 100 h. The decay (13) is highly constrained by the requirement that the decay photons not contribute too much to the background radiation. The decay (12) could satisfy eqn. (14) for masses V₂ above 100 KeV as a result of the non-orthogonality between V_μ and V_e that occurs in models where there is mixing with heavy right-handed or sterile neutral leptons. It has been pointed out recently [19] that in this case the branching ratio for decay (13) is sizeable (of order a) and thus this possibility can be ruled out. Thus it seems likely that if we want some of the usual neutrinos to have masses above 100 eV we must introduce abnormal decays or interactions. Interest-has recently centered on possible roles of Majorons. As noted earlier, in the triplet Majoron (TM) model the neutrinos annihilate into Majorons as soon as they become non-relativistic. In this case they do not remain long enough to help in galaxy formation. In the singlet Majoron (SM) model we discussed this. Annihilation does not take place. The decay v₂ →v₁ Majoron does not occur at tree level in this SM model because the majorons couple diagonally likes the mass. Recently Gelmini and Valle [20] have discussed an extension of the SM model involving several singlet Higgs bosons which allows this decay to occur at a sufficiently rapid rate. The use of such a decay mechanism in a scenario for galaxy formation is discussed in Kolb's talk. In this model the energy density of the present universe is radiation dominated by the background v₁ +Majoron. An alternative to the TM model has recently been given by Pal. It is literally a TE model in that the term (7) is introduced with an extremely small value of p so that the majoron acquires a small mass larger than that of the heaviest neutrino V_τ. For example V_τ might be 10 KeV whereas the Majoron could be 100 KeV. The heavy neutrinos now disappear into light neutrinos as a result of the Majoron exchange; for example:

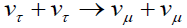
The cross-section is chosen so that this reaction goes out of equilibrium when most of the v_τ (now non-relativistic) have disappeared but enough remain to dominate the present energy density of the universe and to help in galaxy formation.

There exists a reasonable but not compelling theoretical motivation for the violation of total lepton number and consequent non-zero Majorana masses for neutrinos. If neutrinos have a mass, we expect lepton flavor violation associated with neutrino mixing; this shows itself most directly in neutrino oscillation experiments. There are many other possible mechanisms for lepton flavor violation, some unconnected with neutrino masses, that may be searched for in processes like K_L →μe , etc. If neutrinos are stable, satisfy cosmological constraints and have masses that scale with the generation like quarks (or like charged leptons), then the only way to search for neutrino mass is to pursue neutrino oscillation experiments. If one or more neutrinos have a mass well above 100 eV they must disappear by decay or interaction at a sufficiently early time during the lifetime of the universe so as to satisfy cosmologists. This is done most simply by theorists by inventing invisible decay modes or new interactions involving Majorons; such models appear quite contrived. On the other hand more normal decay modes such as 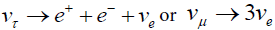are severely constrained by combining cosmology with experiment and can probably be excluded.