Italian Mortality Time Series Underline Hidden Dynamics that Reveal Unexpected Links between COVID-19 Epidemic and North-South Divide
Received: 22-Dec-2022 / Manuscript No. JIDT-22-84499 / Editor assigned: 26-Dec-2022 / PreQC No. JIDT-22-84499 (PQ) / Reviewed: 09-Jan-2023 / QC No. JIDT-22-84499 / Revised: 16-Jan-2023 / Manuscript No. JIDT-22-84499 (R) / Published Date: 23-Jan-2023 DOI: 10.4172/2332-0877.1000523
Abstract
The temporal correlation structure between the profiles of all-causes mortality relative to Italian regions highlighted a largely, unexpected result. Notwithstanding the elimination of well-known seasonal effects, the time series of fluctuations in death rates with respect to the 2015-2019, showed a very high mutual correlation among the 20 Italian regions under scrutiny, ruling out any ‘randomness’ hypothesis. On the contrary, the standardized death rates dynamics was almost invariant along the years, giving rise to a major ‘size’ principal component correspondent to the among regions shared motion, and a second ‘shape’ component modelling the North-South antiphase behaviour. The COVID-19 epidemic, while affecting the breadth of mortality incidence, did not change the among regions correlation dynamics, thus suggesting that this contingency impinges on an intrinsic death rate dynamical mode. The exceptional increase in mortality in the Northern regions observed in 2020 was of the same entity of the North-South differences in mortality observed in ‘normal’ periods. A coherent and homogeneous distribution of mortality rates would had be expected if COVID-related death were to be attributed (solely) to the pathogenic potency of the virus. Conversely, differences in mortality trends across the North-South divide may likely reflect differences in health care availability or other societal features.
Keywords: COVID-19 all-causes mortality; Public health; Complex networks; Human ecology; Population dynamics; Principal component analysis
Introduction
The impact of COVID-19 pandemic on all-causes mortality, while offering a powerful point of view for investigating the nature of this event in Italy, allows highlighting some crucial features of human population dynamics. Such a dynamics, because of the “social animals” very nature of human beings, has deep societal implications. Herein we focus on all-causes mortality in Italy in the years 2020-2021. We used an interdisciplinary approach to the analysis of demographic data trying to unravel the underpinning structure driving the Italian mortality trends along the recent years.
The main motivation of this study relays in the need to rationalize the dramatic difference in demises across Italian regions during the COVID pandemic. This difference was macroscopic, especially in the so-called COVID ‘first wave’, when 86% of fatalities concentrated in four regions of Northern Italy. Lombardia (hosting 15% of Italian population) accounted by alone for around 55% of COVID-associated deaths [1]. This led to a statistically significant difference in 2020 whole Italy mortality with respect to the 2015-2019 period. Noticeably, the striking quantitative North-South mortality difference vanishes in 2021 data. Moreover, with the exception of some short periods, no significant increase in the mortality trend emerges when the overall mortality data are matched with the series from years 2016-2019 (Figure 1) [2].
Noticeably, the time course of both fatalities and Intensive Care Unit accessions (ICUs), during the February 2020-August 2021-time windows, displays the same shape in whole Italy, without significant differences between the diverse administrative regions. Such an evidence suggests the invariance of epidemic underlying dynamics, even though raw data surfaced with very different intensities across Italian regions [3]. This invariance prompted us to look for the presence of latent drivers of mortality shaping the temporal distribution of all- causes mortality at the scale of months. The search for such drivers followed two complementary and mutually independent lines of investigation:
• The investigation of stable differences in death rate between Northern and Southern Italy.
• The exploration of still unknown dynamical modes of mortality fluctuations with respect to both crude mortality rate and well-known seasonal effects.
The first part of the present work investigates the remarkable North- South gradient in mortality and its correlation with both population age structure, and socio-economic descriptors. The second part deals with the death normalized rates, according to month-specific 2015-2019 mortality average data, at the single region level. We found out that these fluctuations are very far from being random, showing a patent temporal correlation among Italian regions in both “pandemic” and ‘non pandemic’ periods. Nevertheless, the nature of these dynamical modes is still elusive and deserves further investigation.
Materials and Methods
In order to measure temporal correlations between different regions devoid of any seasonal effect, we represented each variable (Region) by an 18-component vector: each component is the percent variation with respect to the five-year 2015-2019 average mortality relative to the particular region for each month. Thus, the primary data of the analysis were the percent of variation with respect to the 2015-2019 period relative to the specific region for a specific month spanning the time window going from February of ith year to the next year August. The choice of the time window stems from the mortality data made available by the National Institute of Statistics (ISTAT) at the date of manuscript preparation for the 2020-2021 pandemic time. The normalization for month and region rules out possible biases due to both well-known seasonal effects (all-causes mortality changes across months) and death rate spatial heterogeneity described in Section 1.
We analysed, by independent Principal Component Analyses (PCAs), six different 18 month data sets (seasons) corresponding to 2015-2016, 2016-2017, 2017-2018, 2018-2019, 2019-2020, 2020-2021 respectively. The last (2020-2021) season totally matches the pandemics, the 2019-2020 only partially covers the pandemics in its second part (from February to December 2020), while the other four seasons can be considered as ‘comfort zones’. All the six data sets gave rise to a two component solution explaining around 80% of total variance. Moreover, the loading of the variables (regions) on the first two components pointed to an identical meaning of the components across the different data sets: first component was a ‘size’ (all loadings with the same sign) while second component was a ‘shape’ component with opposite sign loadings for the North and South regions. This pattern allowed us to use first component eigenvalue as a synthetic descriptor of each data set degree of correlation, while the eigenvalue of the second component was a proxy of the entity of North-South divide.
The scores of the two principal components, in each data set, were the regressor of the models having as dependent variable general mortality at both global (Italy) and macro-areas (North, Centre, and South) levels. The same analyses were performed on the whole time series going from 2015 to 2021. The average pairwise temporal correlation of each region with other regions was used as a ‘centrality’ index. The correlation of this index with other region descriptors were evaluated by bivariate linear regression.
Results
Structural divergence in mortality in Northern and Southern Italy: A focus on Lombardia and Campania regions
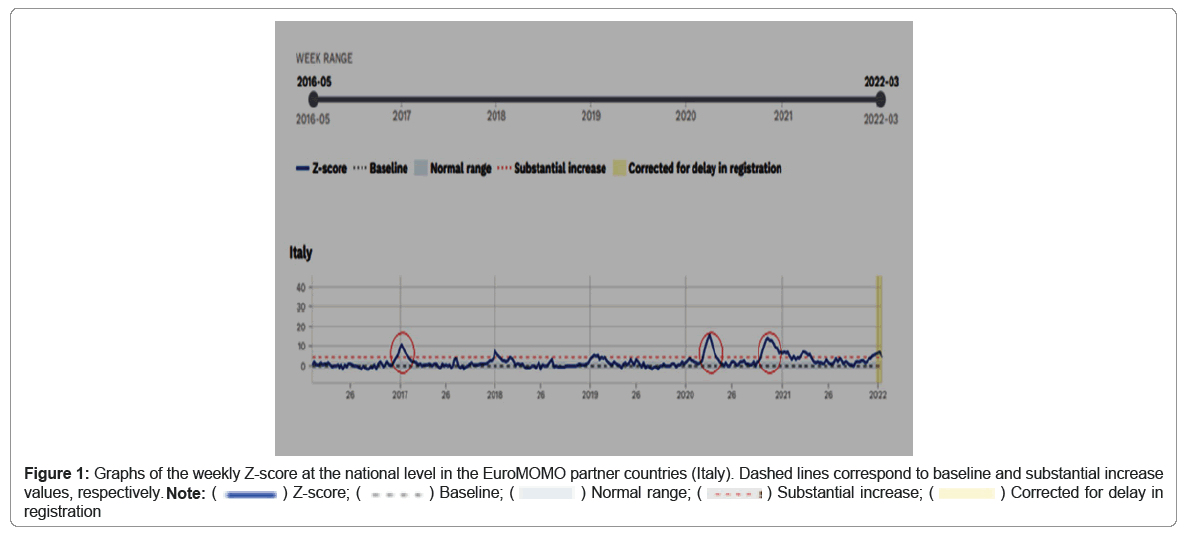
Figure 1 reports all causes mortality trends along with 2016-2021 period in terms of z-scores, as reported in the EuroMomo website. A simple look at the graph highlights that a critical significant increase in deaths, allegedly Covid-related, can only be recorded along the 2020, during the so-called “first Covid wave”. As we will see in the following, this excess is mainly due to the sharp rise in mortality rate in Northern regions.
The rationale in choosing Lombardia and Campania regions, as proxies for the mortality dynamics in North and South of Italy, besides being regions with the highest population densities, relies in their wide difference in several health and socio economic factors. Those features make these regions a sort of markers of the well-known socio-economic divide that characterize the northern and southern territories of the country (Figure 1) [4].
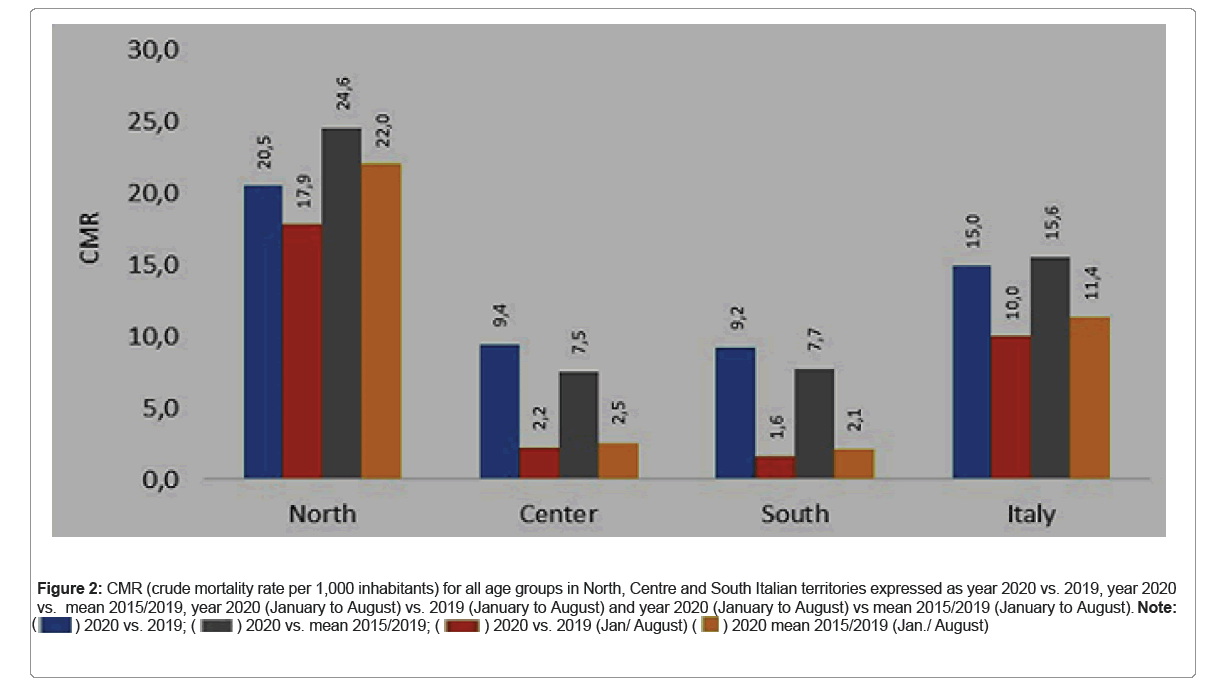
Figure 2: CMR (crude mortality rate per 1,000 inhabitants) for all age groups in North, Centre and South Italian territories expressed as year 2020 vs. 2019, year 2020 vs. mean 2015/2019, year 2020 (January to August) vs. 2019 (January to August) and year 2020 (January to August) vs mean 2015/2019 (January to August). Note:
The life expectancy in Italy shows a wide range of average values, spanning from 80.8 (men) and 85.4 years (women) in Lombardia to 78.7 (men) and 83.4 years (women) in Campania, making Campania the region the one with the lowest life expectancy in Italy. Such an evidence is mirrored by the standardized mortality rate per 100.000 inhabitants, in the age group 0-74 years (SMR0-74), displayed by Campania and Lombardia in the years 2019 and 2020. However, the last edition of the Mevi report [5] highlights that Campania in 2019 and Lombardia in 2020 showed the same number of demises (317 per 100.000 inhabitants), as reported in Table 1. Two southern regions, Campania and Sicilia, scored highest, both in 2019 and 2020. These data are rather surprisingly, as 2019 was the year just preceding the Covid pandemic, that caused in Lombardia, the epicentre of the pandemic surge, a 34.6% of crude mortality rate increase-age group 0-74 year- (CMR0-74) as compared to 2019 [6]. In Campania such an increase was 14.1% (less than the half of Lombardia), even though the SMR0-74 was 10.2% higher than Lombardia and 12.6% higher than 2019. Sicilia experienced a CDR0-74 of 5.6% and a SMR0-74 of 8.4% higher than 2019 and 1.5% higher than Lombardia in 2020 (Table 1).
| Region | 1SMR0-74 2019 | Region | 1SMR0-74 2020 | Region | 2,3CMR0-74 2019 | Region | 2,3CMR>74 2020 |
|---|---|---|---|---|---|---|---|
| Campania | 317 | Campania | 357 | Liguria | 3.31 | Liguria | 13.19 |
| Sicilia | 297 | Sicilia | 322 | Campania | 3.26 | Piemonte | 11.86 |
| Calabria | 287 | Valle d’Aosta | 319 | Valle d’Aosta | 3.21 | Valle d’Aosta | 11.36 |
| Sardegna | 283 | Lombardia | 317 | Piemonte | 3.18 | Friuli | 10.74 |
| Molise | 279 | Liguria | 314 | Molise | 3.15 | Emilia | 10.67 |
| Basilicata | 277 | Molise | 313 | Sardegna | 3.14 | Marche | 10.54 |
| Liguria | 271 | Piemonte | 311 | Lombardia | 3.09 | Lombardia | 10.51 |
| Piemonte | 270 | Calabria | 303 | Sicilia | 3.02 | Toscana | 10.2 |
| Lazio | 268 | Sardegna | 303 | Friuli | 2.9 | Molise | 10.15 |
| Valle d’Aosta | 266 | Basilicata | 291 | Calabria | 2.87 | Umbria | 9.99 |
| Puglia | 258 | Puglia | 288 | Basilicata | 2.84 | Abruzzo | 9.51 |
| Abruzzo | 257 | Abruzzo | 284 | Abruzzo | 2.82 | Veneto | 9.24 |
| Friuli | 255 | Lazio | 281 | Puglia | 2.79 | Basilicata | 9.15 |
| Lombardia | 245 | Friuli | 278 | Emilia | 2.74 | Trentino | 8.97 |
| Emilia | 243 | Emilia | 276 | Lazio | 2.68 | Sardegna | 8.35 |
| Toscana | 242 | Toscana | 261 | Toscana | 2.66 | Sicilia | 8.21 |
| Veneto | 237 | Trentino | 259 | Veneto | 2.54 | Puglia | 8.2 |
| Trentino | 232 | Veneto | 258 | Marche | 2.54 | Calabria | 7.99 |
| Marche | 230 | Marche | 257 | Umbria | 2.53 | Lazio | 7.86 |
| Umbria | 230 | Umbria | 254 | Trentino | 2.41 | Campania | 6.92 |
| Italy | 262 | Italy | 292 | Italy | 2.90 | Italy | 9.41 |
| Northern regions | 252 | Northern regions | 291 | Northern regions | 2.93 | Northern regions | 10.63 |
| Central regions | 243 | Central regions | 263 | Central regions | 2.65 | Central regions | 9.08 |
| Southern regions | 282 | Southern regions | 308 | Southern regions | 3.02 | Southern regions | 7.97 |
Table 1: SMR (Standardized Mortality Rate) and CMR (Crude Mortality Rate) for all causes years 2019 and 2020 in Italian regions listed according the number of demises (higher first).
The SMR0-74 average values for the southern regions (Abruzzo, Molise, Campania, Puglia, Basilicata, Calabria, Sicilia and Sardegna) exceeded the Italy mean by 5.1% in 2020 and 7.2% in 2019, while the central regions (Toscana, Umbria, Marche and Lazio) scored lower than the Italy mean by 7.6% in 2019 and 9.9% in 2020. The northern regions (Piemonte, Valle d’Aosta, Lombardia, Trentino, Veneto, Friuli, Liguria and Emilia) scored lower than the Italy mean by 3.4% in 2019 and equalled it in 2020.
The CMR0-74 is slightly different among regions spanning from 3.31 (Liguria) to 2.41 (Trentino). In this case, a clear-cut trend, depicting a diversity among the northern, central and southern regions, is lacking. Different is the case of CMR>74, that spans from 13.19 (Liguria) to 6.92 (Campania). The high scores of this index is consistent with the age mean and median for COVID-19 deaths identified by ISTAT [7] (2020) in 80.2 years and 82 years, respectively.
A further analysis of Table 1 shows that, during 2020, in Lombardia the 23.3% of deaths occurred within the 0-74 class (and consequently the 76.7% occurred in the >74 year class). In Campania, the two classes accounted for 35.1% and 64.9% of deaths respectively. That is to say, in Campania a higher mortality rate, driven by an excess of mortality in younger classes, was observed independently from COVID pandemics.
Figure 2 shows the comparisons among regional mortality (all age groups) in the years 2019, 2020 and the mean of five years (2015/2019), both for the whole years and the time window spanning from February to August of the next year (18 months), in Italian regions pooled as function of their geographical location. The northern regions show a similar trend in all the comparisons (mean 21.3 ± 2.8 SD), while the central and southern regions show very different pattern both in comparison to the northern region and to the period of the year. The January-August time windows was chosen as proxy of the so-called “first pandemic wave” that struck the country in a very different way in different Italian territories.
From data of Figure 2, it seems clear that “the first epidemic wave” (January/August 2020) significantly raised the overall mortality only in the north part of the country in comparison to the same periods of 2019. The same trend also applies when data are compared to the averaged values of the 2015/2019 period, as both Central and Southern regions experienced a limited mean increase of 2.1 (± 0.4), while data from the North are significantly higher (20.5 ± 2.9). Comparing the whole year 2020 with both 2019 and 2015/2019 mean mortality, the Northern regions displayed a CMR of 22.6 (± 2.9), again a higher value than Centre and South of Italy (8.5 ± 1.2)
The so-called “second epidemic wave”, starting on October 2020, increased the mortality all over Italy, showing a more pronounced trend in the Northern regions. Again, both central and southern regions showed a significant reduced mortality trend when compared to the North (Figure 2). Overall, these data point out that:
• The increase in mortality in 2020 was mainly restricted in the northern regions and particularly severe in the age group >74 years.
• Even though Campania and Sicilia showed the highest scores in the SMR0-75, their increase in mortality, compared to the year 2019 or the mean 2015/2019, is by far lowest than in northern regions.
All in all, the above data point to the existence of a ‘whole Italy’ shared mortality dynamics together with a markedly North-South divide. We will now go more in depth into the nature of these modes, giving a proof-of-concept, as they were a sort of ‘natural modes’ of the system on which Covid epidemic impinged.
Italian death rate as a dynamical system: Discovery of coherent spatio-temporal behaviour
Strategy of analysis: A universal feature of state transitions is the increase in correlation at ‘tipping point’ [8-10]. When approaching to a transition, the degrees of freedom of the system decrease. This provokes an increase in self-correlation (in both space and time) with respect to its ‘comfort zone’. In fact, at equilibrium, the internal fluctuations are minor and mainly stochastic; on the contrary, when an external stressor (any driving force) impinges on the system, the entity of fluctuations increases and the consequent need to dissipate the influx of energy, increases system self-correlation.
The most evident example of this behaviour is the liquid-gas state transition in an heated pan, signalled by the emerging of convective cells in which the initial random Brownian motion of molecules changes into a coordinated motion (we can appreciate at naked eye) of ‘hot’ molecules coming up to the surface and ‘cold’ molecules going down [11]. This behaviour is universal, totally irrespective of the nature of studied system: Figure 3 reports the drastic increase in temporal correlations of price fluctuations of London stock-exchange bonds relative to independent (Figure 3) [12].
Figure 3: In the figure, the nodes of the panels correspond to different firms quoted at London stock exchange. A line linking two different nodes correspond to a pairwise correlation between price fluctuations during the day of two companies bonds, dashed lines point to medium strength correlations, solid lines to high correlation. The lack of any connecting edge corresponds to the lack of significant correlation. Approaching a big financial crisis (right panel) the amount of correlation drastically increases (modified upon permission from ref [12] ).
We adpted the conceptual model depicted in Figure 3 to the temporal correlation of all-cause mortality fluctuations across different regions in Italy. We equated the COVID-19 epidemics to an incoming stress affecting the system. The 20 Italian regions correspond to the firms in Figure 3. London stock exchange and the between firms pairwise price fluctuations are equated to correlations of death rate fluctuations among different regions. The different days of Figure 3 correspond to the 18 months temporal windows encompassing both ‘business as usual’ and critical periods. Our initial hypothesis was that COVID-19 should increase the correlation between mortality fluctuation profiles relative to the different regions.
Given, speaking of temporal correlations potentially induced by an external stressor and must keep at minimum the confounding effects due to other causes. Thus, it is used as primary data the percent of variation with respect to the 2015-2019 period relative to a specific region for a specific month.
This means each Region is represented by a 18-component vector: each component is the percent variation with respect to the five-year 2015-2019 average mortality relative to the particular Region for each month, the considered monthly values spanning the time window going from February of ith year to the next year August.
The choice of this time window was dictated by the mortality data available at the date of manuscript preparation. The normalization for month and region stems from the need to exclude possible biases due to both well-known seasonal effects (all-causes mortality incidence changes across months), and death rate spatial heterogeneity, as described in Section 1.
The starting hypothesis was that stochastic fluctuations in principle very weakly correlated in death rates distribution between Regions, drastically increases their correlation by the effect of Covid epidemic. The intensity of induced correlation corresponds to the amount of variation explained by the main principal components of the perturbed system with respect to the variance spectrum of the principal component solution relative to the ‘normal periods’ [12]. The inspection of component loading pattern (component loadings are the Pearson correlation between original variables, here the 20 Region vectors, and extracted components) in turn allows to ‘give a name’ to the order parameters shaping the among regions correlations and thus to get a characterization of epidemics spreading.
We took into consideration, by independent Principal Component Analyses (PCAs), six different 18 month seasons corresponding to 2015-2016, 2016-2017, 2017-2018, 2018-2019, 2019-2020, 2020-2021 respectively. The last (2020-2021) season totally matches the epidemic, the 2019-2020 only partially covers the epidemics in its second part (from February to December 2020), while the other four seasons can be considered as ‘comfort zones’ according to [12].
Pandemics impinges on pre-existent dynamical modes
Looking at Tables 2A and 2B we can notice the presence of a main first principal component (Factor 1) explaining the 68% of total variance and a second component accounting for 15% of variance (Factor 2). Keeping in mind components are each other linearly independent by construction, this means that the spatio-temporal fluctuations of all-causes mortality is very far from being random given only two factors account for the 83% of 20 regions variability. The components are extracted as eigenvectors of Pearson correlation matrix, thus the solution does not correlate with the actual entity of fluctuations across regions but only to their temporal coherence.
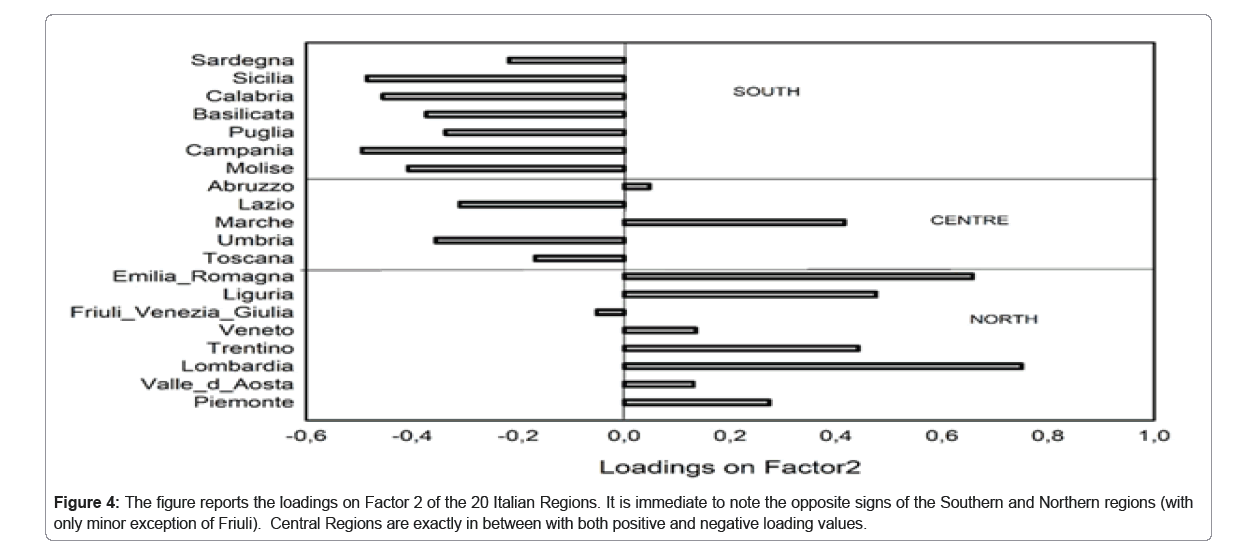
Factor 1 is a ‘size’ component [13], image in light of the global coherence of temporal distribution of temporal fluctuation across all the regions. As a matter of fact, all the regions have positive (and near unity) loading on Factor 1 with the only notable exception of Lombardia that is maximally loaded on Factor 2, and Calabria that is maximally loaded on a singular component in which is the only variable with a relevant correlation Factor 3. Factor 2 is a ‘shape’ component describing a clear ‘North-South’ gradient with all Northern regions with positive (with only exception of the small Friuli region) and all Southern regions with negative loadings as evident in Tables 2A and 2B and Figure 4.
| Component | Eigenvalue | Explained Variance (%) | Cumulative (%) |
|---|---|---|---|
| 1 | 13.59 | 68 | 68 |
| 2 | 3.09 | 15.5 | 83.5 |
| 3 | 1.09 | 5.45 | 88.98 |
Table 2A: PCA solution relative to the February 2020-August 2021 time window distribution of variance explained across factors.
| Loading Pattern | ||||
|---|---|---|---|---|
| Region | Factor 1 | Factor 2 | Factor 3 | Macro Area |
| Piemonte | 0.92568 | 0.30179 | 0.05331 | North |
| Val d’Aosta | 0.90666 | 0.15598 | 0.10112 | North |
| Lombardia | 0.56005 | 0.77013 | 0.24557 | North |
| Trentino/Alto Adige | 0.85568 | 0.44228 | -0.08882 | North |
| Veneto | 0.80011 | 0.15391 | -0.44509 | North |
| Friuli Venezia Giulia | 0.83331 | -0.02683 | -0.45783 | North |
| Liguria | 0.81842 | 0.50118 | 0.06892 | North |
| Emilia-Romagna | 0.70928 | 0.6817 | 0.0835 | North |
| Toscana | 0.95637 | -0.1362 | 0.15479 | Centre |
| Umbria | 0.87189 | -0.33158 | -0.03021 | Centre |
| Marche | 0.81614 | 0.44202 | 0.18088 | Centre |
| Lazio | 0.8911 | -0.2764 | -0.09976 | Centre |
| Abruzzo | 0.95893 | 0.07707 | -0.00596 | Centre |
| Molise | 0.79459 | -0.37861 | -0.12503 | South |
| Campania | 0.83747 | -0.4657 | 0.09458 | South |
| Puglia | 0.86559 | -0.30493 | 0.07471 | South |
| Basilicata | 0.85406 | -0.35153 | -0.124 | South |
| Calabria | 0.49948 | -0.44621 | 0.64641 | South |
| Sicilia | 0.73639 | -0.47844 | 0.17115 | South |
| Sardegna | 0.83836 | -0.19539 | -0.1703 | South |
Table 2B: PCA solution relative to the February 2020 – August 2021 time window loading matrix.
This result tells us that the normalized temporal fluctuations in all causes mortality are highly coherent across all regions, with only a relatively minor (15%) but very coherent-variance component accounting for the North-South gradient.
After having collected the information dispersed into 20 variables (regions) into three macroareas (North, Center, South) and to whole Italy, we checked the ability of the two main factors-deriving from between region correlation matrix-to predict the fluctuations patter for macroareas and whole Italy .
Top panel reports the oscillation in time of the Factor 1 and Factor 2 scores (the scores have by construction zero mean and unit standard deviation). It is worth noting the presence of a shared peak at March- April 2020 (second and third point) along a global pattern that is by construction independent for Factor 1 and Factor 2 correspondent to March-April 2020, the crucial phase of first Covid wave. Bottom panel reports the regression line of whole Italy temporal fluctuations (y-axis) vs Factor 1 (left panel) and the regression line between Italy actual temporal fluctuation and the estimated value by multiple regression having both Factor 1 and Factor 2 as independent variables.
It is immediate to note how March 2020 and April 2020 outliers in bivariate regression (left panel) are absent in multiple regression (right panel) being correctly modelled by the addition of Factor 2 (North- South divide) to the model. The two models reported in Tables 2A and 3, together with the models relative to the Macro Areas (North, Centre, South).The percentage of variance explained (R2) is 83% for bivariate (only Factor 1, shared variance across Regions) and goes up to 98% (so reaching a practically complete explanation) in complete model 2 (Table 3).
| R2 | P | ||
|---|---|---|---|
| Model 1 Italy | 13.72+16.27* Factor 1 | 0.83 | <0.0001 |
| Model 2 Italy | 13.72+16.27* Factor 1+6.35*Factor 2 | 0.98 | <0.0001 |
| Model1 | 19.10+22.85* Factor 1 | 0.58 | <0.0003 |
| North | |||
| Model2 | 19.10+22.85* Factor 1+18.73* Factor 2 | 0.98 | <0.0001 |
| North | |||
| Model 1 Centre | 7.99+11.00* Factor 1 | 0.94 | <0.0001 |
| Model 2 Centre | 7.99+11.00* Factor 1-1.44* Factor 2 | 0.95 | <0.0001 |
Note: * Signifies the Factors
Table 3: Models including Factor 1 and both Factor 1 and Factor 2 for the whole Italy and different Italian territories.
As expected, while bivariate (only Factor 1) model is sufficient to predict Central Italy pattern (practically identical R2 for the two models). A dramatic increase in explicability (going from 58% to 98%) is obtained for the Northern regions when passing from bivariate to multiple regression. Southern Italy has a remarkable (even if not as extreme as North) increase in fitting by inserting Factor 2 as additional regressor. These results tell us that the ‘Northern Singularity’ in Covid related deaths is clearly noticeable in terms of between regions correlations, as highlighted by both Factor Loading pattern (Lombardia and Emilia Romagna are partially decoupled by the Factor 1 ‘shared’ motion with extremely high loading Factor 2, see Table 2A and of by the parameters of the regression models.
The spatial heterogeneity coming from Factor 2 is mirrored by the Pearson correlation between the temporal profiles of different areas (Table 4)
| Area | Italy | North | Centre | South |
|---|---|---|---|---|
| Italy | 1 | 0.96 | 0.84 | 0.67 |
| North | - | 1 | 0.67 | 0.44 |
| Centre | - | - | 1 | 0.93 |
| South | - | - | - | 1 |
Table 4: Pearson correlation between the temporal profiles of different macro-areas.
While all the temporal patterns are each other positively correlated, as expected by the presence of a leading (Factor 1) shared size component, the presence of a striking North-South gradient is evident from the decreasing correlation with increasing distance along the gradient. This is particularly evident as for North pattern having a relatively low correlation coefficient with South (r=0.44), with Centre in intermediate position (r=0.67). This pattern is mainly a consequence of the singular concentration of COVID related fatalities in the North (especially in the first wave) while Centre and South did not experience this singularity (r=0.93 between Centre and South).
This bi-partition of Italy into two neatly separated areas during the epidemic is still more striking looking at the between macro- areas correlation partialled out of the shared correlation with whole Italy pattern. Table 5A reports the between areas partial correlation coefficient on which shared correlation with whole Italy is eliminated. This operation practically corresponds on focusing on the sole Factor 2 source of variation (Tables 5B and 5C).
| Area | North | Centre | South |
|---|---|---|---|
| North | 1 | -0.96 | -0.99 |
| Centre | - | 1 | 0.9 |
| South | - | - | 1 |
Table 5A: Partial correlation coefficients between Areas depurated by the effect of Whole Italy. Partialling out the shared correlation of the areas with Whole Italy, corresponds to eliminate the effect of Factor1 and keeping alive only area profiles variability depending upon minor components (mainly Factor 2) refer to February 2020-August 2021.
| Area | North | Centre | South |
|---|---|---|---|
| North | 1 | -0.96 | -0.99 |
| Centre | - | 1 | 0.9 |
| South | - | - | 1 |
Table 5B: Refer to the February 2020-August 2021 and February 2019- August 2020 periods respectively refer to February 2019- August 2020 periods respectively.
The between areas correlation partial correlation coefficients depurated by the effect of the whole Italy variable display a near to unity negative correlation between North and the other areas (reaching an almost unit negative value for North South relation), with Centre nearer to South in both periods (2020/2021 vs. 2019/2020)
The analysis of the pre-pandemic period (2019-2020), encompassing only the ‘first wave’ in the second part of the time window, gives largely superimposable results with respect to 2020-2021 pandemic season as evident by both the explained variance spectrum, and the partial correlation pattern. This result mirrors the presence of a size ‘shared’ dynamics (Factor 1) and a North-South gradient.
It is worth noting this practically perfect superposition between fully pandemic (2020-2021) and ‘partially pandemic’ (2019-2020) temporal windows going hand-in-hand with different average mortality fluctuations as evidenced in Table 6.
| Area\Season | 2019-2020 | 2020-2021 |
|---|---|---|
| Italy | 3.98 (15.20) | 13.72 (17.62) |
| North | 9.28 (28.03) | 19.10 (29.78) |
| Centre | -0.52 (6.53) | 7.99 (11.34) |
| South | -0.63 (4.94) | 9.73 (4.94) |
Table 6: Fluctuations in the average mortality (expressed in %+Standard Deviation) in February 2019- August 2020 and February 2020- August 2021 periods, with respect to 2015-2019 period.
Table 6 reports the fluctuations in the average mortality with respect to 2015-2019 period. It is worth noting the evident effect of Covid that in the first wave (the only one represented in 2019-2020 time window) is practically restricted to North, with both South and Centre with near zero average fluctuations. Going to 2020-2021 (fully epidemic period) , the inclusion of the second and third waves spreading all over Italy, even central and southern regions present positive fluctuations with respect to baseline, besides the order of magnitude is much lower than North. Notwithstanding these relevant quantitative difference in terms of mortality rate, the shape of the underlying modes explaining temporal dynamics are largely invariant between the two periods. This result points to a very strong ‘latent structure’ shaping Italian mortality dynamics that is not affected by contingent stress like Covid epidemic.
What is worth noting is the extremely high temporal standard deviation of mortality rates (Table 6): keeping in mind we are dealing with two time windows that, even if at different extent, include the SARS-COV2 ‘stressor’, the hypothesis of a correlation induced by the epidemic is tenable. The temporal variation can be ascribed by the oscillation of epidemic that has a marked seasonal effect due to the well- known drastic decrease of respiratory infections during summer. When passing to the analysis of the four ‘business as usual’ time windows (2015-2016, 2016-2017. 2017-2018, 2018-2019) we had very puzzling results.
Our initial work hypothesis stemmed from the idea that, having eliminated both region and seasonal effects on mortality fluctuations, the ‘business as usual’ time windows should present a mainly stochastic temporal structure with a much less ordered structure. This feature could be ascribed to a higher dimensionality of the phenomenon, due to the lack of epidemic-induced ordering, with the system occupying a comfort zone [12].
This was not the case: all the four ‘normal’ time windows displayed very similar principal component structures, and partial correlations between areas with respect to ‘critical’ periods (Tables 5A and 5B). This largely invariant correlation structure originates from relatively small fluctuations but maintains an extremely high temporal standard deviation (Figure 5) .
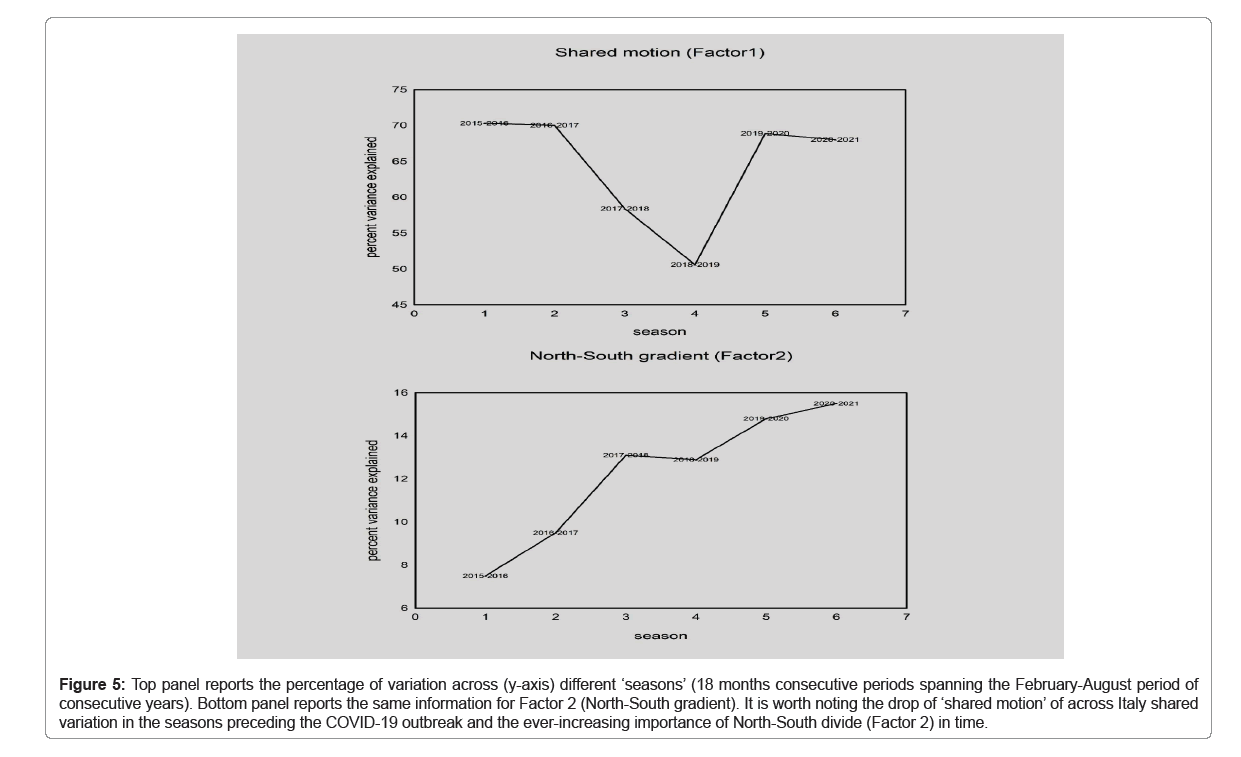
Figure 5: Top panel reports the percentage of variation across (y-axis) different ‘seasons’ (18 months consecutive periods spanning the February-August period of consecutive years). Bottom panel reports the same information for Factor 2 (North-South gradient). It is worth noting the drop of ‘shared motion’ of across Italy shared variation in the seasons preceding the COVID-19 outbreak and the ever-increasing importance of North-South divide (Factor 2) in time.
This means that the two factors, corresponding to ‘shared oscillation’ and ‘North-South gradient’ respectively, were not a mere consequence of epidemic induced ordering; instead, they are ‘structural’ and thus reflect some pre-existent features mortality dynamics in Italy. This situation can be equated to the dynamics of a structure (e.g. a protein molecule) in which the native configuration generates the ‘typical modes’ of the dynamics that can only increase in intensity (e.g. increasing temperature, here corresponding to pandemic times) but keeping invariant the correlation between different parts [14].
That is to say that the fluctuation’s coherence is an essential (and not induced by external stressor, as per our initial hypothesis) feature of all- causes mortality. Figure 6, reports the amount of variance explained by the first two components along the different 18-months seasons taken into consideration ( Figure 5).
Figure 5 shows how the main component (Factor 1, shared motion) goes to a minimum (even keeping a fairly high percent of explained variation) in the two ’18 months seasons’ before the onset of pandemics. This pattern only partially justifies our initial hypothesis of epidemic acting as order parameter. On the contrary, the North-South gradient increases its relative role (in terms of percent of variance explained) along subsequent seasons, telling us that this mode becomes progressively more imp ortant in time. According to the reach of a partial ‘comfort zone’ just before the onset of pandemic, the monotonic increase in relative importance of Factor 2 stops at 2017-2018 and 2018- 2019 seasons contemporary to the decrease of order of Factor 1 shared motion component.
The presence of a continuously increase in the North-South divergence, constitutes a dramatic warning signal in terms of public health and mirrors and increasing economic and social divide with large public health consequences that going far beyond the pandemic crisis.
To go more in depth into the characterization of the mortality dynamics, we adopt a network approach borrowed from molecular dynamics analysis [15]. We considered the Italian regions as nodes of a network, whose edges are the Pearson correlations between death rates time courses. We analysed separately 2015-2016 and 2020-2021 periods. This choice allowed us to compare the ‘two temporal extremes’ of the scrutinised phenomenon, so to check for the robustness of the between regions correlation in mortality fluctuations (when “depurated” from common seasonal effects).
Given the predominant effect of the first component (Factor 1, whole Italy shared motion) in terms of explained variance, we expect that the between region pairwise correlations will be dominated by this mode.
This was actually the case, with very high Pearson correlation values in both the considered time windows. The 2015-2016 and 2020- 2021 correlation matrixes are reported as supplementary material, the relative statistics (mean and standard across regions correlation coefficient) are pretty similar, and are reported in Figure 6 ( centrality 1=2015-2016 correlation; centrality 2=2020-2021 correlation), and does not vary so much between the two seasons (delta correlation=centrality 1-centrality 2). The (slight) decrease in average correlation going from 2015-2016 is mainly due to the ‘eccentric behaviour’ of Calabria, Lombardia and Emilia during the epidemic (see bottom line graph).
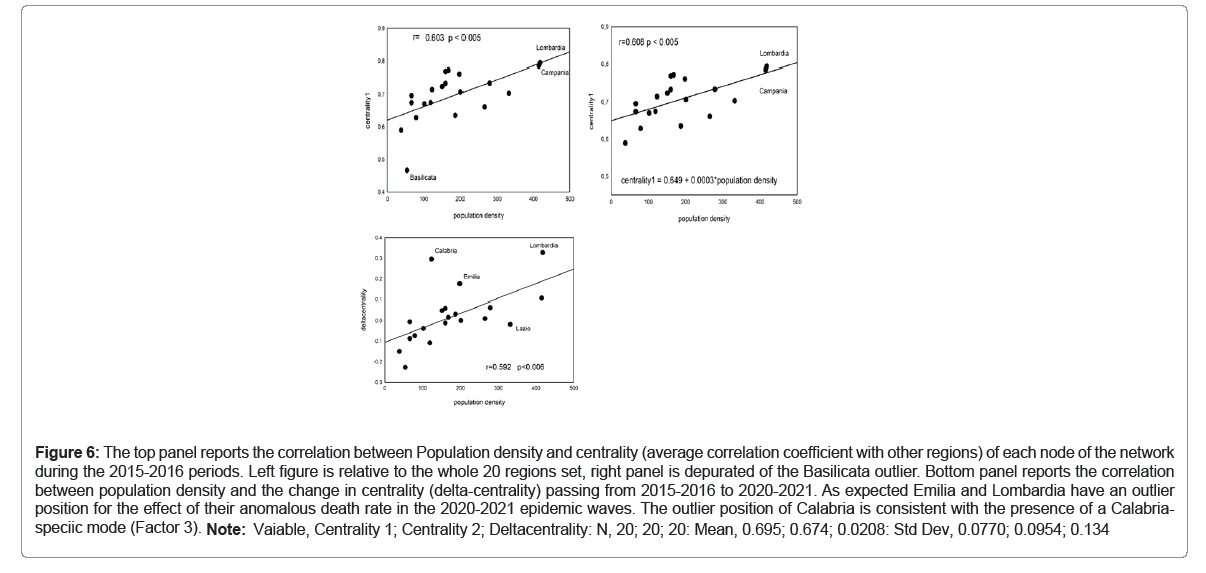
Figure 6: The top panel reports the correlation between Population density and centrality (average correlation coefficient with other regions) of each node of the network during the 2015-2016 periods. Left figure is relative to the whole 20 regions set, right panel is depurated of the Basilicata outlier. Bottom panel reports the correlation between population density and the change in centrality (delta-centrality) passing from 2015-2016 to 2020-2021. As expected Emilia and Lombardia have an outlier position for the effect of their anomalous death rate in the 2020-2021 epidemic waves. The outlier position of Calabria is consistent with the presence of a Calabria- in few regions (Figure ). 6 The results reported in Figure 6 confirm the above hypothesis: the The plots of Figure report the relation of the ‘centrality’ of each 6 coefficient) are pretty similar, and are reported in Figure (centrality 6 speciic mode (Factor 3). Note: Vaiable, Centrality 1; Centrality 2; Deltacentrality: N, 20; 20; 20: Mean, 0.695; 0.674; 0.0208: Std Dev, 0.0770; 0.0954; 0.134
The plots of Figure report the relation of the ‘centrality’ of each region (correspondent to the average correlation coefficient with other regions) with population density (Number of inhabitants/Surface). The statistically significant correlation between population density and centrality in ‘normal’ condition suggests that Italy can be considered as a relatively homogeneous dynamical system as for mortality patterns in time. As expected, this correlation vanishes during epidemic due to the singularity of some regions as evident in the bottom plot. The outlier position of Basilicata fits with this interpretation given the isolated position of this region from the main fluxes of both people and goods across Italy.
The results reported in Figure 6 confirm the above hypothesis: the most ‘central’ (i.e. most representative) regions in terms of mortality time pattern (top panels) are the ones with higher population density (i.e. Lombardia and Campania). This is exactly what we do expect by the sampling of a homogenous Italian population as for mortality temporal profiles: the samples corresponding to the higher population density are the ones most representative of the entire population status. The puzzling point is that our starting data are all-causes mortality rates both spatially (region-by-region) and temporally (month-by- month) normalized. In these conditions, we should not expect any relevant Pearson correlation between the different regions all-causes standardized mortality rates that, even if with a relatively similar averages, should mirror a mainly stochastic time course with a substantial lack of temporal correlations. On the contrary we observe a very high average between regions temporal correlation (Average Pearson r=0.695 and 0.674 for 2015-2016 and 2020-2021 periods) suggesting the existence of a still unexplored internal ‘source of coherence’ different from well- known seasonal patterns.
The average correlation (centrality) of different regions slightly decreases going from ‘business-as-usual’ to pandemics time window, being this decrease mainly driven by the singular mortality distribution in few regions (Figure 6).
To our knowledge, the only paper taking seriously the problem of non-stochasticity of mortality rates when corrected for both age structure and seasonal effects was that from O’Hare and Li [16] that analysed the residuals of different mortality models relative to a number of nations. Computing the Hurst exponents, the Authors found clear evidence of long-range temporal correlation in mortality ‘residuals’ in all the analysed time series. In order to have a more comprehensive view of the temporal structuring of standardized mortality rates all along the entire studied period between January 2015 and August 2021, we considered the entire period on a month-by-month, region-by- region basis obtaining the following results (Tables 7A and 7B).
| Component | Eigenvalue | Explained Variance (%) | Cumulative (%) |
|---|---|---|---|
| 1 | 13.74 | 68.68 | 68.68 |
| 2 | 2.26 | 11.32 | 80 |
| 3 | 0.78 | 0.04 | 83.92 |
Table 7A: The table reports the explained variance distribution of the major 3 components of the between regions correlation structure across the whole 2015-2021 period.
| Loading pattern | ||||
|---|---|---|---|---|
| Region | Factor 1 | Factor 2 | Factor 3 | Macro Area |
| Piemonte | 0.90982 | 0.3022 | -0.09773 | North |
| Val d’Aosta | 0.73949 | 0.29066 | -0.27569 | North |
| Lombardia | 0.68374 | 0.6338 | 0.29295 | North |
| Trentino/Alto Adige | 0.80957 | 0.4725 | 0.04339 | North |
| Veneto | 0.84534 | 0.19609 | -0.29677 | North |
| Friuli Venezia Giulia | 0.8251 | 0.08223 | -0.39166 | North |
| Liguria | 0.83299 | 0.43816 | -0.00261 | North |
| Emilia-Romagna | 0.82939 | 0.49859 | 0.18403 | North |
| Toscana | 0.938 | -0.08409 | -0.03844 | Centre |
| Umbria | 0.8049 | -0.33583 | 0.05385 | Centre |
| Marche | 0.88406 | 0.13049 | 0.32528 | Centre |
| Lazio | 0.8204 | -0.26852 | -0.13545 | Centre |
| Abruzzo | 0.9017 | -0.06832 | 0.06679 | Centre |
| Molise | 0.79773 | -0.35693 | 0.14543 | South |
| Campania | 0.87145 | -0.36749 | -0.08391 | South |
| Puglia | 0.90518 | -0.22385 | 0.0555 | South |
| Basilicata | 0.73554 | -0.33387 | -0.06921 | South |
| Calabria | 0.73876 | -0.40456 | 0.38195 | South |
| Sicilia | 0.82001 | -0.38892 | 0.03331 | South |
| Sardegna | 0.8322 | -0.15767 | -0.13788 | South |
Table 7B: The corresponding loading pattern.
The results relative to the entire time window from 2015 to 2021 are superimposable with the presence of a ‘shared variance’ first principal component and a second component relative to the North-South gradient. Again, we observe the negative partial correlation between North and South macro-areas patterns when depurated of their common relation with whole Italy profile (Table 8)
| Area | North | Centre | South |
|---|---|---|---|
| North | 1 | -0.895 | -0.977 |
| Centre | - | 1 | 0.779 |
| South | - | - | 1 |
Table 8: Partial correlation coefficients between fluctuation profiles of the three different areas depurated from their correlation with the Whole-Italy profile. The correlations are relative to the entire February 2015-August 2021 time window. The results are superimposable to those of the analyses on the different 18 months windows.
Discussion
Analysis of the dynamics of the standardized mortality rates occurring in the 18 months windows as well as in the entire 2015-2021 period let us to describe a superimposable dynamical pattern. In both cases a ‘shared’ and ‘North-South gradient’ oscillatory trends appears as stable structures within which the CMR is framed. These trends drastically increased in intensity during the pandemic period but maintain their general shape, telling us they constitute a structurally invariant property of mortality distribution in Italy. The Covid-19 epidemic did not generate any new dynamics but amplified the entity of fluctuations of a pre-existing dynamical system, in the same way as an increase in temperature exacerbates the oscillatory modes typical of a given structure (e.g. a protein molecule, or any other structured object) without altering it, at least within a specific temperature range. The nature of these modes is still unknown but, as for the North-South gradient, we can get some hints by considering the two most representative regions of the North and South macro-areas (Lombardia and Campania) in terms of two age classes (0-74 and >74 year). Being the SMR0-74 identical in Campania in 2019 and in Lombardia in 2020, the only difference that can be seen is the short time-span of the deaths anomaly, the onset of which occurred in Lombardia from week 11 to week 19. In Campania, in 2019 the highest mortality was recorded in January, and then it declined up to April and remained roughly constant up to December (ISTAT, 2020). Probably, this difference is mirrored by the second dynamical mode pointing to a strong driving of socio-economic and infrastructural difference between Italian regions.
Our study has some limitations regarding the selected data set, as we utilised the all-cause mortality across Italy through the chosen time-frame, instead of taking into consideration “COVID mortality” (i.e., lethality) data. Indeed, we consider COVID lethality records faulty by two main biases:
a) Over-notification and/or under-notification of COVID deaths. As reported by Islam [17], a dropping of 73% of COVID-19 demises occurred in the official records when Public Health England changed its definition of COVID-19 deaths in July 2020. Furthermore, Rancourt [18] pointed out the all-cause mortality as the most useful parameter in investigating the epidemiology of the pandemic. On the contrary, Whittaker, et al. [18] estimated that an under-notification of COVID-19 deaths biased the statistics. The least that can be said is that there is no agreement on the meaning and number of COVID-19 deaths, making these figures unreliable. The all-cause mortality, that should increase in the midst of a pandemic, is not affected by personal and/or governmental interpretations of the data, and is by far more reliable that other proxies for the analysis of the epidemic [19,20].
b) The RT-PCR test, as designed by Cornam, et al. [19], seems to be unreliable in the sidetrack of “COVID cases” as it is unable to discriminate between SARS-Cov-2 and influenza viruses, according to the American Centres for Disease Control [20]. Zhang et al. pointed out the false-negative results that jeopardize the effectiveness of the test in describing the real impact of the epidemic, whereas Verna, et al. [21-23] cast doubt the usefulness of RT-PCR swabs for tracing the evolution of SARS-COV-2 pandemic, because the huge number of both false-positive and false-negative results depriving the test of the necessary trustworthiness. Again, the least that can be said is that the RT-PCR test does not meet criteria stringent enough for side tracking “COVID-cases”.
The resilience of the mortality pattern across Italian regions during COVID-19 epidemic requires some comments. Albeit the overall burden of causalities increases significantly, a clear symmetry breaking does not appear, as confirmed by the fact that the system recovers the same trend both in shape and in quantitative terms-during the year 2021. However, the persistence of the North-South gradient is at odds with the infectious nature of COVID-19. A coherent and homogeneous distribution of mortality rates would had be expected if Covid-related deaths should be ascribed to the pathogenic potency of the virus. Differences in mortality trends across the North-South divide may likely reflect differences in health care availability or other societal ffeaftures [24,25].
Conclusion
This may surmise that difference in population features (age, co- morbidities, exposure to specific environmental pollutants, etc.) can also play a very relevant role. Indeed, the outstanding mortality increase observed in some northern regions has already been put in correlation with some environmental constraints. Indeed, long-term air-quality data significantly correlated with cases of COVID-19 in up to 71 Italian provinces, providing further evidence that chronic exposure to atmospheric contamination may represent a favourable context for the spread of the virus. These specific features should be interpreted alongside with the death rate distribution across different age groups. The vast majority of casualties has been recorded in elderly people, sharing not less than three co-morbidities. According to the Italian Statistical service (ISTAT), excess mortality for all causes) in 2020 would be due to for 96% to deaths of people over 65. Again, this finding suggests that the clinical outcome is highly dependent on the specificity of the virus-host interactions, as shaped by patient’s previous medical history and environmental/societal context. Within this perspective, the reliability of COVID-19 as a syndemic deserves to be reconsidered and investigated.
References
- Dorrucci M, Minelli G, Boros S, Manno V, Prati S, et al. (2021) Excess mortality in Italy during the COVID-19 Pandemic: Assessing the differences between the first and the second wave, Year 2020. Front Public Health. 16:9-669209.
- Graphs and maps, Euromomo, 2022.
- Bizzarri M, Di Traglia M, Giuliani A, Vestri A, Fedeli V, et al. (2020) New statistical RI index allow to better track the dynamics of COVID-19 outbreak in Italy. Sci Rep22:22365.
- Petrelli A, Di Napoli A, Sebastiani G, Rossi A, Giorgi Rossi P, et al. (2019). Italian atlas of mortality inequalities by education level. Epidemiol Prev 43:1-120.
- Atlante Mevi, Mevi, 2021.
- Demography in numbers, DemoISTAT, 2021.
- The trend of deaths in the period 1 January - 31 December for the years 2015-2020. Advance data for the year 2020 on the integrated database of municipal daily mortality, ISTAT National Institute of Statistics, 2020.
- Gorban AN, Tyukina TA, Pokidysheva LI, Smirnova EV (2021) Dynamic and thermodynamic models of adaptation. Phys Life Rev 37:17-64.
- Bizzarri M, Pontecorvi P (2021) Critical transition across the Waddington landscape as an interpretative model: Comment on "Dynamic and thermodynamic models of adaptation" by A.N. Gorban et al. Phys Life Rev. Sep 38:115-119.
- Scheffer M, Carpenter SR, Lenton TM, Bascompte J, Brock W, et al. (2012) Anticipating critical transitions. Science 338: 344-348.
- Gorban AN, Smirnova EV, Tyukina TA (2010). Correlations, risk and crisis: From physiology to finance. Phys A: Stat Mech Appl 389: 3193-3217.
- Jolicoeur P, Mosimann Je (1960) Size and shape variation in the painted turtle. A principal component analysis. Growth. 24:339-354.
- Amadei A, Ceruso MA, Di Nola A (1999). On the convergence of the conformational coordinates basis set obtained by the essential dynamics analysis of proteins' molecular dynamics simulations. Proteins: Struct Funct Genet 36: 419-424.
- Arnold GE, Ornstein RL (1997) Molecular dynamics study of time-correlated protein domain motions and molecular flexibility: Cytochrome P450BM-3. Biophys J 73:1147-59.
- Colin O, Youwei L (2016) Modelling mortality: Are we heading in the right direction? Appl Econ 49: 170-187.
- Islam N (2022) “Excess deaths” is the best metric for tracking the pandemic. BMJ. 4:376-o285.
- Rancourt DG (2020) All-cause mortality during COVID-19: No plague and a likely signature of mass homicide by government response.
- Whittaker C, Walker PGT, Alhaffar M, Hamlet A, Djaafara BA, et al. (2021) Under-reporting of deaths limits our understanding of true burden of covid-19. BMJ 375:n2239.
- Corman VM, Landt O, Kaiser M, Molenkamp R, Meijer A, et al. (2020) Detection of 2019 novel coronavirus (2019-nCoV) by real-time RT-PCR. Euro Surveill 3:2000045.
- Control (CDC’s Laboratory Outreach Communication System (LOCS), American centres for disease, 2022.
- Zhang Z, Bi Q, Fang S, Wei L, Wang X, et al. (2021) Insight into the practical performance of RT-PCR testing for SARS-CoV-2 using serological data: A cohort study. Medrxiv 2:e79-e87.
- Verna R, Alallon W, Murakami M, Hayward CPM, Harrath AH, et al. (2021) Analytical performance of COVID-19 detection methods (RT-PCR): Scientific and societal concerns. Life (Basel) 11:660.
- Fattorini D, Regoli F (2020) Role of the chronic air pollution levels in the Covid-19 outbreak risk in Italy. Environ Pollut 264:114732.
- Italian public institution, ISTAT, 2021.
- Courtin E, Vineis P (2021) COVID-19 as a syndemic. Front Public Health 9: 763830.
Citation: Dumontet S, Giuliani A, Falco GD, Fedeli V, Bizzarri M (2023) Italian Mortality Time Series Underline Hidden Dynamics that Reveal Unexpected Links between COVID-19 Epidemic and North-South Divide. J Infect Dis Ther 11: 523. DOI: 10.4172/2332-0877.1000523
Copyright: © 2023 Dumontet S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 2910
- [From(publication date): 0-2023 - Nov 17, 2025]
- Breakdown by view type
- HTML page views: 2440
- PDF downloads: 470

 registration
registration