Research Article Open Access
Innovative Wind Turbine Selection Method using Modified Weibull Probability Function
1Professor in Mechanical Engineering, University of Jordan, Jordan
2Lecturer, University of Philadelphia, Philadelphia, PA 19144, USA
- *Corresponding Author:
- Hammad M
Professor in Mechanical Engineering
University of Jordan, Jordan
Tel: + 962 7 77421354
E-mail: hammad@ju.edu.jo
Received Date: March 23, 2015 Accepted Date: April 30, 2015 Published Date: May 10, 2015
Citation: Hammad M, Batarseh L (2015) Innovative Wind Turbine Selection Method using Modified Weibull Probability Function. J Archit Eng Tech 4:139. doi:10.4172/2168-9717.1000139
Copyright: © 2015 Hammad M, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Architectural Engineering Technology
Abstract
In this work, a three-year wind data for some sites in Jordan was analyzed. Two sites showed highly promising potential. Both predicted more than 1.0 MWh/m2.y.
This work modified the probability function of Weibull – Hiester and Pennel to produce more accurate potential speed values for the wind. Results showed that this modification enhanced energy potential by 30%.
The interaction of wind turbine performance data with site wind data was then discussed. The yearly output energy of different machines was the objective function for an optimization process with rating velocity (Vr) as the main variable. The resulted optimum energy was found to depend on the two variables of the Wiebull function. Optimum Vr was found to range from 4.2 to 5.6 for the sites considered.
The optimum Vr can be used as a selection parameter for the best suitable turbine.
Keywords
Wind energy; Corrected Weibull formula; Optimum wind energy potential
Introduction
Due to the soaring of energy prices and the environmental deterioration impact of energy generation, scientists and decision makers began looking for alternative sources of energy and a special focus on the possibility of using clean energy sources that have a low impact on environment. Two sources of energy grasped a high level of attention; wind and solar energy. They were sought as the best solution for green buildings and energy sources.
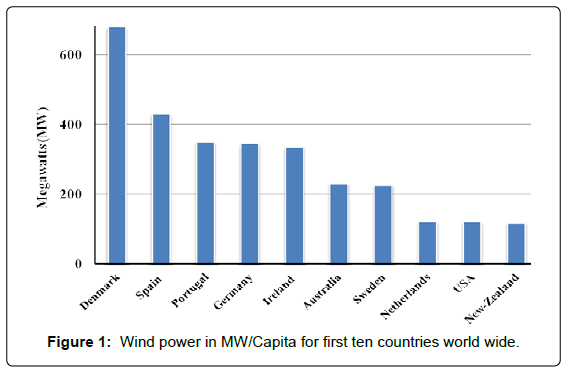
Wind energy was harnessed by mechanical means since the dawn of history. For the last 20 to 30 years, its unit construction and total built units increased rapidly. Reasonable amount of production was listed for around 30 countries worldwide. The highest production of wind energy countries in GW/billion GDP are shown in Table 1 and the highest MW/Capita list is exhibited in Figure 2. Leading countries are Denmark, Portugal, Spain, Germany and Ireland, [1] (Table1) (Figure 1).
| Country | Production | Country | Production |
|---|---|---|---|
| Denmark | 18.5 | Sweden | 6.0 |
| Portugal | 16.0 | China | 4.5 |
| Spain | 15.0 | New Zealand | 4.2 |
| Germany | 9.0 | Bulgaria | 4.0 |
| Ireland | 8.0 | Greece | 3.7 |
Table 1: list of top countries that produce wind energy in GW/GDP.
The worldwide wind power capacity reached 200 GW in 2010 [2].
A step forward in wind energy technology was achieved by using off shore technology. This was observed in Scotland where the aim is to reach full renewable energy before the mid of the century. The expected power rating is to reach 68 GW from off shore fields of the Highlands long shores and Islands district, north of Scotland [3].
The wind energy showed comparatively low cost compared with other methods of renewable energy [4]. A reasonably comparable low cost of kWh of wind energy reached this year (2012) around C€ 4.2 / kWh.
Ababneh, et al., [5] found that wind energy is an appropriate energy alternative to face the high generation cost and increasing demand on electrical energy in Jordan. Also, Al Zoubi, [6] found out that it is essential to transfer from using small experimental wind energy systems to using large grid connected systems in Jordan, as large wind farms are very important to establish reliable alternative sources of energy.
Alghoul, et al., [7], tried to introduce a modified Weibull distribution formula and use it in wind analysis for five different sites in Jordan. Ras muneef site showed best opportunity and potential for wind power generation. In addition, Badran and Abdulhadi, [8], used a method of fuzzy logic to analyze wind energy use for four different selected sites in Jordan based on both benefits and costs. Results showed that power increases as turbine swept area increases.
Sabra, [9] showed a map of wind velocity of Jordan and concluded that sites such as Al-Ibrahimyya and Hofa possess the highest potential for wind power generation. Ras Muneef and Hofa are in north of Jordan and each site has an experimental unit of 4 MW capacity and a third site is at Fujaje at south of Jordan where a wind farm is on schedule for operation within a year, Ammari and Al-Maaitah, [10].
In the work of Andrade, et al. wind data was analyzed by numerical methods to determine Weibull formula parameters. This formula is commonly used to predict yearly wind velocity distribution. The formula contains two parameters: shape factor, k and scale factor [11,12].
Data collected from two coastal sites was used in this study. Six numerical methods were used to calculate Weibulls parameters for both sites. The parameters were calculated using power distribution instead of velocity distribution. Authors argued that their results produced curves in a better conformity than the curves commonly used before which were depending on velocity distribution.
The authors, Arsalan, et al. [13], presented and adopted a new method to calculate Weibull parameters. This method was called L – MOM, L- Method of Moment. The authors believed that this method is suitable in cases of limited wind speed data. L-MOM method was compared to other methods including the Mont Carlo simulation and was found to be more actual than the others.
A single site in The Sahara desert, Algeria, and for one year long, wind data was collected and discussed in Dahaib, et al., [14], work. Weibull density distribution was used and monthly power patterns were also calculated. The authors ended to a conclusion that the Weibull parameters had a wide effect on the predicted power values. Adding the power predicted at this site of the Sahara was highly attractive economically.
The work of Mohammadi, et al. [15], investigated wind energy generation potential in a single site in the city of Zarrineh in Iran. The analysis was carried out using two methods: standard deviation and power density methods. Power density method was superior to the other one. This site was found to be feasible but with low power generation capabilities.
The work of Kharo, [15] investigated the potential of power production of one site in south Pakistan. Wind speed distribution and wind power density methods were used in this analysis. Wind generated by a commercial wind turbine was estimated all year round. Simulation using Weibull distribution with different methods of calculating the two parameters was followed. A feasibility study was carried out, cost of the kWh production was found to be US$ 0.263 at z production of 10.225 GWh per year [16].
Four sites in the west were chosen for collection of wind velocity data by Kitaneh, et al., [17] Weibull, k and c parameters were found for each site. Monthly mean velocity was used. Energy density was calculated and suitability for power generation was decided. In addition, Several analytical methods were followed in the work of Petkovic, et al. [18] to find the Weibull parameter. Of these methods were the polynomial and radial function, Kernel function of support vector regression. These were used to enhance predictive accuracy and capability for achieved generalization. The support of vector regression was found to be the most accurate method.
The data of ten different sites, chosen at Cape Town/ South African coast by Ayodele, et al. [19] was examined using the root mean square method to achieve the best fit curves for Weibull distribution. This work put into operation 20 wind turbines. The best turbine for use was found of 13 m/s rated wind velocity, 3 m/s cut in velocity and 20 m/s cut out velocity. Rated out put power was 1600 kW.
In Jordan, twenty other sites were put into investigation by researchers most of them are still under investigation. Three of these sites will be investigated in this work namely Safawi and Azraq south at the east of Jordan and Daba’a near Queen Alia airport at Amman area.
Researchers in this field gathered wind velocity data for a period of time varying from 2 years up to 9 years. Mean velocity daily, monthly and yearly wind velocities are calculated. Weibull model of wind pattern can be used, [6]. This model predicts further yearly probable hours in which a certain velocity can occur.
Work Methodology
The sites considered by literature with potential of wind energy in Jordan can be categorized into three levels as follows:
Sites studied thoroughly and experimental units are in operation now such as Ras muneef and Hofa.
Sites that were studied and performance is known such as Fujaje in which a planned wind farm to be put into production soon.
Sites under study such as the chosen three sites in this work which are: Sawawi, Azraq south and Daba’a.
Following steps were followed in this study:
About 1,400 readings for each year along 3 years time from 2008 – 2010 for each site were supplied by the Jordan Metrological Department (JMD). Daily mean wind velocity, monthly mean and yearly mean were calculated.
Figures representing velocity distribution as mean monthly and experimental repetition hours per year were exhibited for each site.
Experimental best curve fit of velocities from 0 to 25 m/s were constructed for each site. On same figures Weibull distribution was shown using Weibull – Heister and Pennel formula. Compression and modifications were corrected for the formal.
The interaction between the Weibull modified formula and the wind turbine performance curve. Basics for selection of optimum turbine were suggested.
Maximum yearly energy (kW.h) that can be extracted by the most suitable wind turbine was calculated and results were compared with each other and with other sites.
Interaction of predicted yearly energy output for typical machine was optimized. The main variable was the rating velocity, Vr.
Discussion
Wind velocity distribution
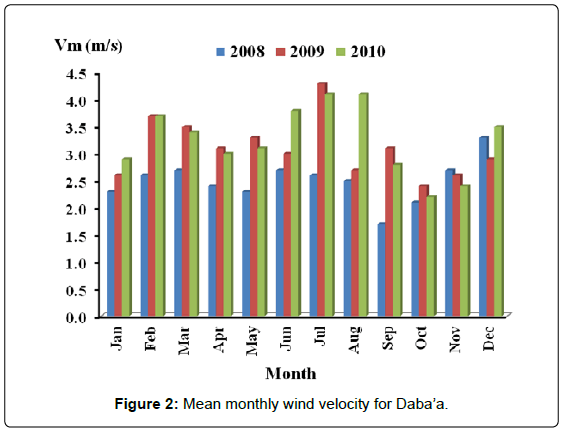
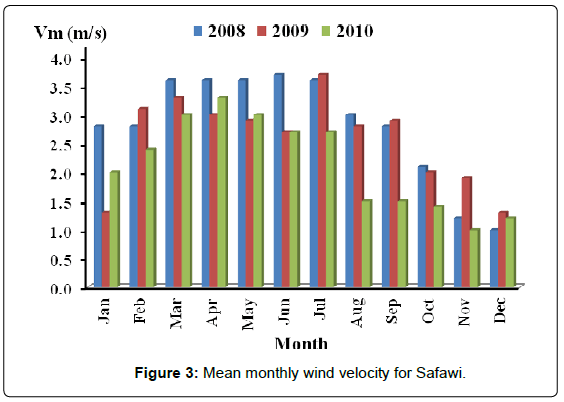
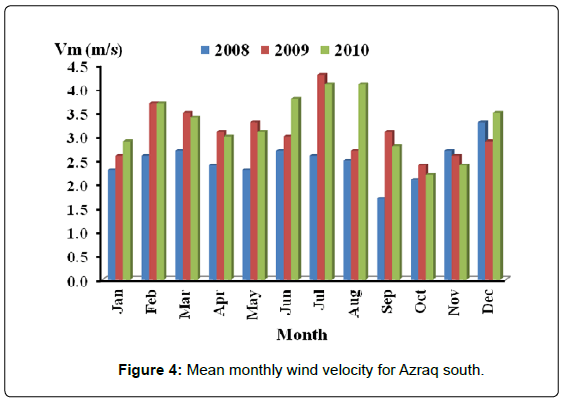
Figures 2-4 show bar distribution of monthly mean wind velocities of the three sites: Daba’a, Safawi and Azraq south for the three consecutive years, 2008, 2009 and 2010. Azraq south possessed the highest value of about 6.2 m/s. even distribution of velocities is around July in Azraq south and in May in Safawi, the high wind speed of December in Daba’a for the three years disturbed any form of even distribution for that site.
Values of monthly mean velocities for sites of Azraq south, Daba'a and Safawi reached 6.2 m/s, 4.2 m/s and 4.0 m/s respectively with respective yearly mean velocity reaching 4.2, 2.9 and 2.7 m/s.
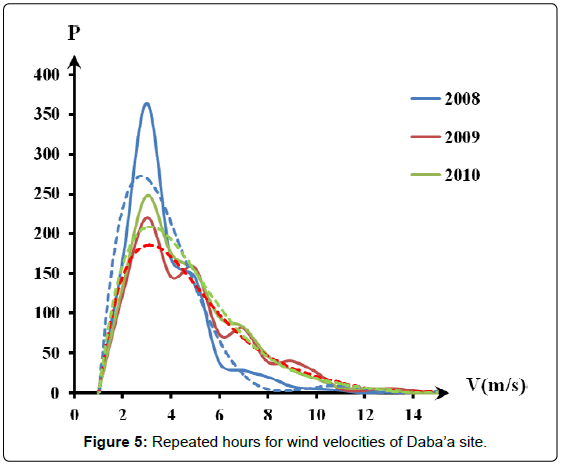
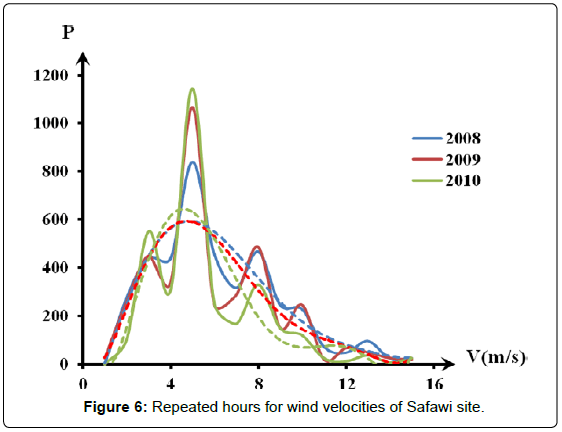
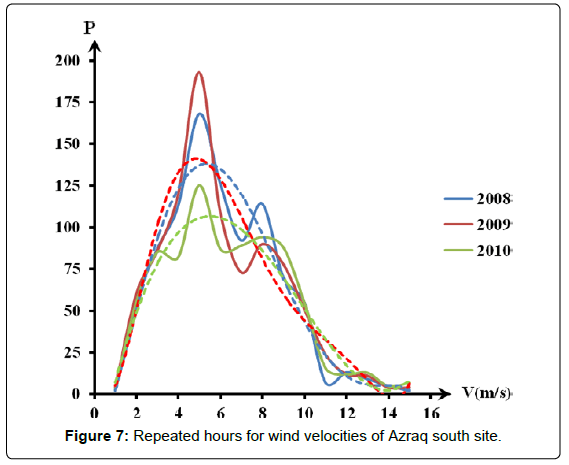
Figures 5-7 show the number of repeated hours having the velocities from 1 m/s up to 25 m/s in each site for the data years. Maximum repeated velocities hours of the year were 3.5 m/s, 4.5 m/s and 5.0 m/s for Daba’a, Safawi and Azraq south respectively with respective repeated hours/year were 370, 1150 and 1900.
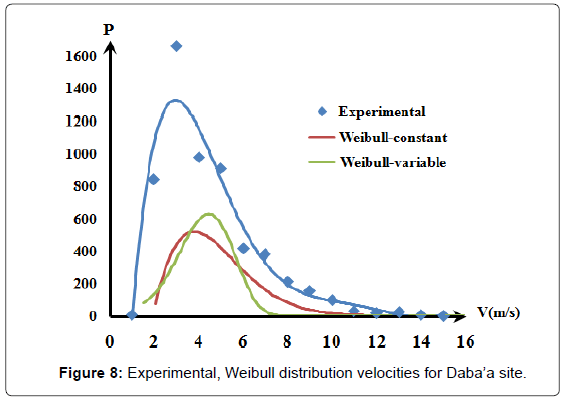
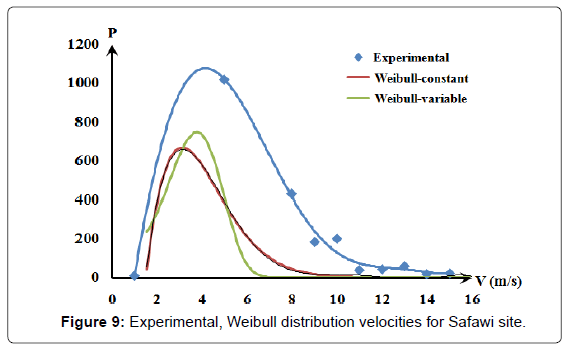
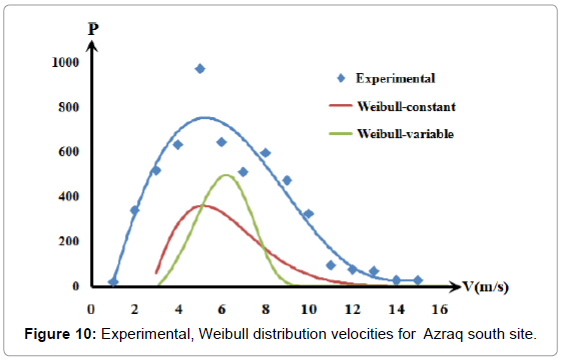
Figures 5-7 were converted into best fit distribution of yearly repetition hours of the wind speed for measured wind speed values. This was shown in Figures 8-10 as experimental collected data results.
Weibull prediction model
The Weibull probability function in the term of Weibull – Hiester and Pennell, 1981 in the form:
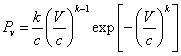 (1)
(1)
Where:
k is the shape factor and
k = 1.09 + 0.20V (2)
c is the scale factor and
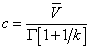 (3)
(3)
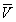 is the mean velocity and Γ is the gamma function.
is the mean velocity and Γ is the gamma function.
In the case of this work the value used in the literature in Equation.2 was not suitable and another form was adopted of the form of
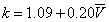 (4)
(4)
Equation curves were shown in Figures 8-10 in two forms:
The first form in the equations was to use variable velocity in Equation. 4 to calculate the shape factor k. This case was called Weibull - variable curves.
The second form, k was calculated using mean velocity. This was called Weibull Constant curves.
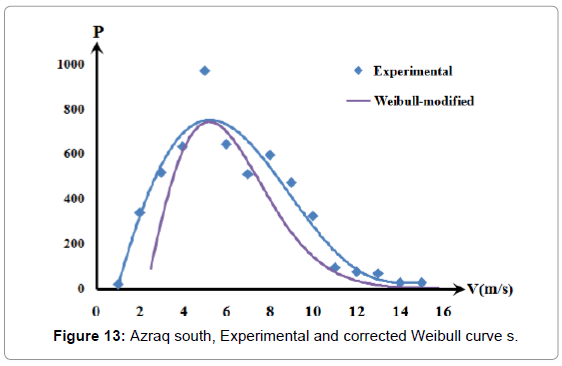
Both the Weibull - constant and the Weibull - variable curves are shown by Figures 8-10. Since the Weibull - constant curves conform in shape with the experimentally measured data, it was decided to use it as Weibull reference. The difference between the experimental curves and that of the Weibull – constant curves as the error, ε, was listed in Table 3 shows a high error is encountered.
The accumulated error represented in Equation.5:
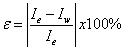
Where: ε is the percentage error, Ie is the area under the fitting curve of the experimental data and Iw is the area under the Weibullmodified curve (Table 2).
| No | Site | ε (%) |
|---|---|---|
| 1 | Daba’a | 88.5 |
| 2 | Safawi | 62.1 |
| 3 | Azraq south | 63.9 |
Table 2: The percentage error between the experimental collected data and the constant Weibull.
It was decided to modify Equation.1 so that Weibull model would be as close as possible to represent the measured data fitting curve. It was found that the best modification for the Weibull model was done by multiplying Weibull function with a correction function has a form given in Equation. 6
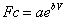 (5)
(5)
Where: a and b are constants shown in Table 3.
| No | Site | a | b |
|---|---|---|---|
| 1 | Daba’a | 1.6 | 0.12 |
| 2 | Safawi | 0.46 | 0.35 |
| 3 | Azraq south | 1.02 | 0.13 |
Table 3: Correction forms for Weibull model.
Mean values for a and b of the best two cases in Table 3 are 1.3 and 0.13 respectively. A common function can be used as;
Fc= 1.3 e0.13 (7)
In this case, the modified Weibull relation will appear as follows:
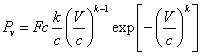 (8)
(8)
Where: Fc is the corrective modification shown in Table 3. k and c are constants with values depend on 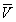 mean velocity.
mean velocity.
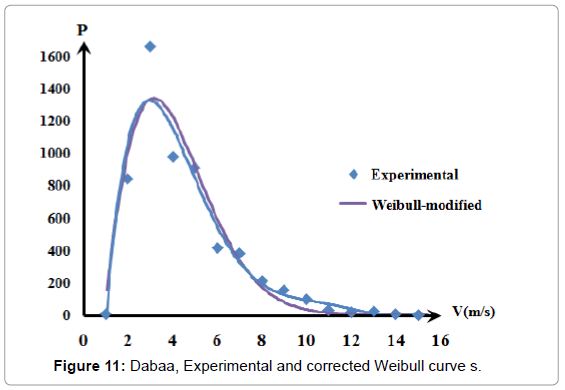
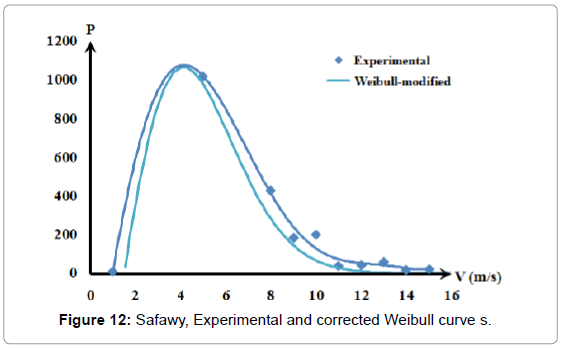
Figures 11-14 show a good conformity pattern between the measured data curves and the Weibull curves with error percentage less than around 5%. This formula increased the probable repetition yearly hours by at least of 30%.
Interaction of site performance and turbine performance
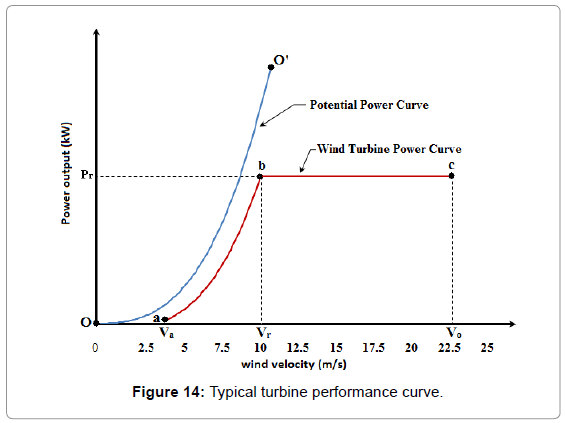
In order to select the best turbine for the analysis, yearly power output should be optimized. The turbine performance given by the manufacturers is shown in Figure11.
The velocities Va, Vr and Vo are the cut-in, rating and cutout velocities while Pr is the rating power which is kept constant as flat power for the velocity range from Vr to Vo.
Using the modified Weibull prediction form, the yearly energy extracted is
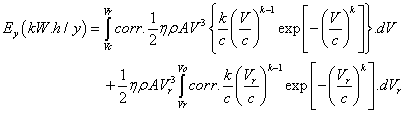 (9)
(9)
Where corr is the correction factor, Fr.
To simplify the integration procedure in Equation.9, the Va is assumed to approach zero. Analytically, the integration in Equation.9 is impossible to be found when (Fc) is substituted in it. However, this issue was solved numerically by applying Taylor series expansion to the correction function Fc.
The convenient order of Taylor that insures a truncation error minimized to less than 1% is the 18th order for all the sites under investigation.
After expanding the correction function and substituting it in Equation the annual expected energy in the unit of kW.h / y can be determined. Optimizing this energy can be obtained when:
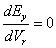 (10)
(10)
The mathematical solution for Equation.11 was found as:
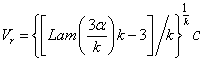 (11)
(11)
Where Lam is abbreviation for the Lambert function and α is exponential value given as:
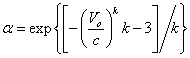 (12)
(12)
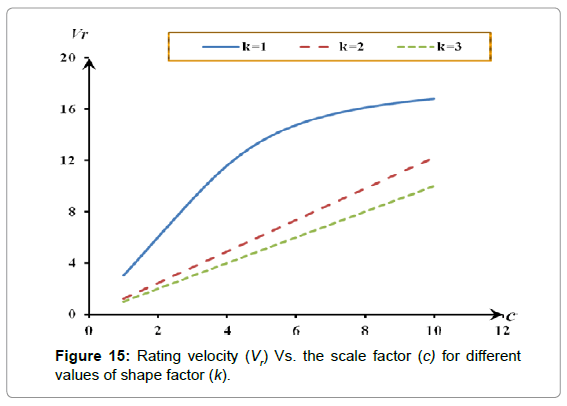
According to Equation.11, the optimum rating velocity (Vr) depends on: Vo, k and c. it was shown from the literature that the most common value for cutout velocity (Vo) for the available wind turbines is 25 m/sec. when the previous value of Vo is substituted in Equation12, the relation between Vr and both k and c is shown in Figure 15. As illustrated, the scale factor (c) affects proportionally on the optimum rating velocity while the shape factor has a reverse effect on the optimum rating velocity.
When Vo=25 m/s is substituted in Equation11, and then solved for the three selected sites, an optimal rating velocities can be obtained. The optimal rating velocities for the selected sites are shown in Table 4.
| No | Site | Vr (m/s) |
|---|---|---|
| 1 | Daba’a | 4.66 |
| 2 | Safawi | 4.17 |
| 3 | Azraq south | 5.60 |
Table 4: The values of optimal Vr for the three selected sites.
Comparing Vr extracted from Figure15. for k and c of Table 5 with values of Table 4, they must be Equation.
| No | Site | 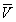 m/s m/s |
K | C |
|---|---|---|---|---|
| 1 | Daba’a | 2.9 | 1.7 | 3.3 |
| 2 | Safawi | 2.5 | 1.6 | 2.8 |
| 3 | Azraq south | .3.2 | 1.9 | 4.3 |
Table 5: the values of 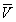 , C and k for the three selected sites.
, C and k for the three selected sites.
The total probable wind energy can be extracted from any site:
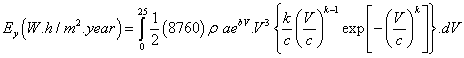 (13)
(13)
Where: ρ is the air density and was assumed 1.25 kg/m3 the factor 8760 is the number of hours in one year. Table 6 illustrates the calculated values for energy for the selected sites, which are exhibited in bar Figure 16.
| Site | Safawi | Daba’a | Azraq south |
|---|---|---|---|
| Energy (kW.h/m2. Year) |
765.9 | 1084.5 | 1688.1 |
Table 6: Energy potential values for the selected sites.
Results and Conclusion
The power that can be extracted from the sites under consideration was compared with that of the sites already considered by previous studies. Two sites showed competitiveness to the previous ones (Table 7).
| Site | Max. monthly, m/s | Month | Yearly mean, m/s | Power potential, kWh/m2y | Power potential |
|---|---|---|---|---|---|
| Daba'a | 4.5 | July | 2.9 | 1084 | High potential |
| Safawi | 4.0 | July | 2.7 | 766 | Low potentiak |
| Azraq south | 4.6 | July | 4.2 | 1688 | High potential |
| RasMuneef | 7.9 | Feb. | 7.4 | 2852 | Max.in Jordan |
| Aqaba | 6.6 | June | 5.7 | 1432 | Mean in Jordan |
| Mafraq | 3.7 | July | 2.9 | 192 | Min. in Jordan |
Table 7: Wind energy generation comparizon with already studied sites.
Table 5 shows that both Daba'a site and Azraq south site possess high potential for wind energy generation. The energy generated by both was more than 1.0 MWh/m2.y.
The under prediction of the Weibull probability function was clear in shown Figures 8-10. A correction function was proposed to shift the prediction to be as near as possible to the measured best fit curves. A newly proposed probability function was:
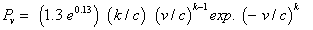 (14)
(14)
This formula increased the probable production of yearly energy by more than 30%.
The interaction of the wind turbine performance with the site performance was considered. Optimization of the objective function, Ey taking Vr as main variables is shown in Equation 11. This Equation showed Vr as function of: Vo, K and C.
It is suggested that the most suitable wind turbine to be used in any site is the one of Vr is Equation to the optimum value.
Acknowledgement
The authors would like to express gratitude for the University of Jordan as this work was prepared during a sabbatical leave for the first author.
References
- Shahan Z (2011) Installed wind power capacity per GDp. clean Technica.
- Editor (2011) world wind power.
- Roberts J (2011) Energy boom.
- Hammad M (1995) Photovoltaic, Wind and Diesel, cost comparative study for water pumping in Jordan. Energy Policy 23: 723-726.
- Ababneh M, Kakish W, Molareb O, Etier I (2009) Investigation of wind energy in Jordan. ICEGES 2009, LeRoyal Amman, Jordan.
- Alzou’bi M (2010) Renewable energy potential and characteristics in Jordan. JJMIE 1: 45-48.
- Alghoal M, Sulieman M, Azmi B, Wahab M (2007) wind energy potential in Jordan. IEJ 8: 71-78.
- Badran O, Abdulhadi E (2009) Evaluation of factors affecting wind power generation in Jordan. The 7th Asian Pacific conference on wind engineering, Taipi, Taiwan.
- Sabra Z (1999) wind energy in Jordan – use and perspectives. Dewi, Amman, Jordan.
- Ammari H, Almaaitah (2003) assessment of wind-generation potentiality in Jordan using the site effectiveness approach energy. Energy 28: 1579-1592.
- Aldohni A (2009) an assessment of potential energy for utility-seale wind power generation for selected locations in Jordan. MSc thesis, University of Jordan.
- Andrade C, Neto H, Rocha A, Eugênia M, Silva V (2014) An efficiency comparison of numerical methods for determining Weibull parameters for wind energy applications: A new approach applied to the northeast region of Brazil. Energy conversion and Management 86: 801-808.
- Arslan T, Bulut Y, Yavuz A (2014) Comparative study of numerical methods for determining Weibull parameters for wind energy potential. Renewable and Sustainable Energy Reviews 40: 820-825.
- Dahbi M, Benatiallah A, Sellam M (2013) The Analysis of Wind Power Potential in Sahara Site of Algeria-an Estimation Using the ‘Weibull’ Density Function. Energy Procedia 36: 179-188.
- Mohammadi K., Mostafaeipour A (2013) Using different methods for comprehensive study of wind turbine utilization in Zarrineh, Iran. Energy conversion and Management 65: 463-470.
- Khahro S, Tabbassum K, Soomro A, Dong L, Liao X (2014) Evaluation of wind power production prospective and Weibull parameter estimation methods for Babaurband, Sindh Pakistan. Energy conversion and Management 78: 956-967.
- Kitaneh R, Alsamamra H, Aljunaidi A (2012) Modeling of wind energy in some areas of Palestine. Energy conversion and Management 62: 64-69.
- Petkovic D, Shamshirband S, Anuar N, Saboohi H, Wahab A, et al. (2014) An appraisal of wind speed distribution prediction by soft computing methodologies: A comparative study. Energy conversion and Management 84: 133-139.
- Ayodele T, Jimoh A, Munda J, Agee J (2012) Wind distribution and capacity factor estimation for wind turbines in the coastal region of South Africa. Energy conversion and Management 64: 614-625.
Relevant Topics
- Architect
- Architectural Drawing
- Architectural Engineering
- Building design
- Building Information Modeling (BIM)
- Concrete
- Construction
- Construction Engineering
- Construction Estimating Software
- Engineering Drawing
- Fabric Formwork
- Interior Design
- Interior Designing
- Landscape Architecture
- Smart Buildings
- Sociology of Architecture
- Structural Analysis
- Sustainable Design
- Urban Design
- Urban Planner
Recommended Journals
Article Tools
Article Usage
- Total views: 14782
- [From(publication date):
March-2015 - Nov 21, 2024] - Breakdown by view type
- HTML page views : 10286
- PDF downloads : 4496