Identification of Optimal Alignment for a Real-World Canal in India
Received: 02-Oct-2023 / Manuscript No. jescc-23-116884 / Editor assigned: 04-Oct-2023 / PreQC No. jescc-23-116884 (PQ) / Reviewed: 18-Oct-2023 / QC No. jescc-23-116884 / Revised: 23-Oct-2023 / Manuscript No. jescc-23-116884 (R) / Accepted Date: 30-Oct-2023 / Published Date: 30-Oct-2023
Abstract
Optimizing the design of irrigation channels is crucial for the effective distribution of water while considering the cost of earthwork in excavation, which is a major cost in the construction of a canal. Changes in precipitation patterns due to climate change can affect the water availability in canals. Therefore, efforts are needed to ensure the continued functionality and sustainability of canal systems in the face of a changing climate. In this research, a methodology has been presented for identifying the optimal alignment for a canal, focusing on the cost of earthwork in cutting and filling. The practicality of the approach presented herein has been demonstrated through its application to real- world canal in Arjun Sahayak Pariyojna in the Mahoba district of Uttar Pradesh, India. The objective function in the optimization process is the total cost of excavation including the cost of earthwork in cutting and filling. Four distinct canal alignments were considered and cost of cutting and filling have been computed for each alignment based upon the topography of the ground for different alignments. The methodology presented herein is robust in nature and can be applied with minimal adjustments to determine optimal canal alignments for other canal systems. The present research has the potential to significantly reduce costs in medium to large-scale irrigation projects.
Introduction
The gap between the demand and supply of water has been widening in most regions of the world, mainly due to increased economic activities, rapid increase in population and increase in per capita water consumption standards. The gap has further widened due to climatic changes (Rehman et al. 2021). Changes in precipitation patterns due to climate change can affect the water availability in canals. Increased rainfall in some regions and prolonged droughts in others can lead to challenges in managing water levels and flows in canals. Therefore, efforts are needed to ensure the continued functionality and sustainability of canal systems in the face of a changing climate. In a developing country such as India, the water availability per capita has gone down to abysmal levels. The situation has become extremely challenging due to the non-uniform distribution of water resources over space and time. A significant amount of losses are suffered by the farmers due to the unpredictable nature of monsoonal rainfall in India. To aid irrigation in water deficient areas, canals are often utilized to deliver water to the fields. Canals are an importance part of infrastructure that provides an efficient way to distribute water to a wide area of agricultural land. With the help of canals, water can be transported over long distances, thereby allowing farmers to irrigate fields that may not have a direct water source nearby. Canals can deliver a relatively uniform and consistent supply of water to agricultural fields, which is a basic requirement for crop growth [1].
The optimal canal design plays a crucial role in maximizing the efficiency, effectiveness, and sustainability of water distribution to agricultural fields. The construction of canal requires huge amount of financial resources, and therefore substantial savings in monetary terms can be achieved through optimization of canal design. Based upon the levels of the natural ground and canal banks, an irrigation channel may be in full cutting, full filling, or partial cutting and filling. The process of optimal design of canal involves determining the best parameters for the canal's physical dimensions while considering costrelated factors. In the context of optimizing the canal section for trapezoidal channels (a common shape for open channels), several parameters need to be considered [2 ]. These parameters include canal bottom width, depth, side slope, and corner radius among others. The design cost for irrigation channels is a crucial aspect of any irrigation project, and it comprises two primary components: excavation cost and lining cost. These costs play a significant role in determining the overall budget of the project and the long-term efficiency and sustainability of the irrigation system. Excavation cost refers to the expenditure incurred on excavating the channels to create the path for the flow of water. There are various factors that influence the cost of excavation [3]. These include the length, width, and depth of the channels, as well as the type of soil or terrain in the project area. Efficient excavation techniques and equipment selection can help minimize costs and reduce project duration. Lining cost refers to the expenditure made in providing protective linings to the irrigation channels. These linings serve various purposes, including reducing seepage, preventing erosion, and maintaining water quality. The choice of lining material depends on factors like soil type, water quality, and budget constraints. The cost of excavation is significantly higher than the cost of lining, and therefore it is important to minimize the cost of excavation in irrigation projects [4].
Designing efficient irrigation channels, therefore, involves careful consideration of excavation and lining costs. Efficient planning, accurate site assessment, and appropriate material selection are crucial factors to manage these costs effectively. Balancing initial investment with long-term benefits is crucial to ensure the sustainability and success of irrigation projects. This ultimately contributes to improved agricultural productivity and water resource management. The optimization process involves using mathematical and computational methods to vary these parameters and minimize the cost of excavation and lining while ensuring that the constraints on hydraulic performance, stability, and regulations are satisfied. The minimum cost design for canals involves minimizing both the cost of cutting and filling. This results in a complex problem with nonlinear objective and equality constraints, making analytical solutions challenging. Therefore, the objective of the present research is to identify a minimum-cost alignment from several alternatives [5 ].
Literature Review
Several researchers have explored the optimization of canal designs, considering factors such as hydraulic efficiency, practicability, and cost-effectiveness. Loganathan et al. (1991) provided optimality requirements for a free board, velocity, and canal-size-constrained parabolic-canal design. Froehlich et al. (1993) assumed that uniform flow and standard depth are frequently the foundation of open-channel design. If a channel is lined with a non-erodible material, the size of the channel can be chosen only based on hydraulic efficiency without considering excessive velocities [6]. Design of a minimum earthwork cost channel section involves minimization of the earthwork cost, which depend on the excavation depth subject to uniform flow condition in the channel (Swamee et al. 2001). Allen et al. (2005) studied minimal volumes of deep percolation in canals in the Imperial Irrigation District. Kentli et al. (2014) describes improved water channel networks for transporting more water while at least maintaining its quality due to the growing need and expanded world population. Bhattacharjya et al. (2007) describes a method to determine a cost-effective channel segment for a given flow rate, longitudinal slope, roughness coefficients, and several other parameters. Swamee et al. (2013) presented the strategy for optimizing the alignment of an irrigation canal. A study by Guo and Shin (2018) demonstrated that public infrastructure investment rises when local governments can reap the benefits of investments in irrigation infrastructure. Several researchers (for example, Kacimov, 1992; Swamee et al. 2000; Chahar, 2005) have introduced canal design approaches that account for loss of water due to seepage [7].
Farzin et al. (2021) utilized a range of evolutionary methods, namely the bat algorithm (BA), particle swarm optimization (PSO), and the hybrid combination (HBP) to create optimal trapezoidal open-channel cross-section configurations that minimized the sum of excavation and concrete lining costs. El-Molla and El-Molla (2021) used SEEP/W model to explore how the seepage in trapezoidal earth canals is impacted by the characteristics of compacted earth linings. The authors demonstrated that utilizing compacted earth linings represents an effective approach for mitigating conveyance losses. Furthermore, the study concluded that partial lining is a viable option, with the most efficient orientation of the lining depending on the width of the canal. Zhang et al. (2022) developed an optimization model based on a genetic algorithm for a two-stage canal system. The model had dual objectives of minimizing the time gap between water delivery and water demand, and reducing fluctuations in the discharge of the main canal. Fan et al. (2023) describes three optimization models for the distribution of canal water, designed for specific scenarios where the total water volume and flow rate in the main canal have already been determined [8 -10].
Study Area
The Mahoba district, with an area of 2884 km2, is located in the southern part of Uttar Pradesh. On the north, it is bordered by the districts of Hamirpur, Banda, Chatarpur, Madhya Pradesh, and Jhansi. Figure 1 shows the location of Mahoba district in the province of Uttar Pradesh. The river Dhasan separates the district's western border from the district of Jhansi. An expansive irrigation project called the Arjun Sahayak Pariyojna is situated in Kabrai, a region tucked away in the Mahoba District of Uttar Pradesh, India. With the help of this project, the Dhasaan River's water supply will be used to support irrigation systems for local agricultural activities. This project aims to increase agricultural production, guarantee water availability, and contribute to general socio-economic development of the region through a properly planned infrastructure [11 ]. The irrigation provided by the Arjun Sahayak Pariyojna to a cultivated command area (CCA) measuring 4259 hectares would have a substantial impact on the local agricultural industry. The project's water supply supports this huge area, enabling farmers to produce their farms profitably and successfully. The normal rainfall in Mahoba district is 864 mm. The weather is typically subtropical with a long and hot summer. The south-west monsoon is responsible for about 87% of the annual rainfall. The hottest month is May, when temperatures of around 470 C are recorded. By about the middle of June, temperatures begin to fall due to the approaching monsoon. Typically, January is the coldest month when the maximum temperature does not exceed 80 C [12-14].
Data and Methodology
The study canal for the present research is the Surauli canal under Arjun Sahayak project in the province of Uttar Pradesh, India. In this research, the topographical data has been collected from government agencies such as the Uttar Pradesh Irrigation Department. The details of the Arjun Sahayak project are provided in Table 1.
| 1. | Name of the project | Arjun Sahayak Project |
| 2. | Location | Kabrai, Mahoba District in UP.(India) Latitude: 26° 59' 58.9920'' N Longitude:79°59' 59.5896'' E |
| 3. | Purpose | Irrigation |
| 4. | Source of Supply | Dhasaan River |
| 5. | Catchment Area | 590.52 km2 |
| 6. | Max. Flood Discharge | 1587.00 m3/s |
| 7. | Cultivated Command Area (CCA) in Ha |
4259.00 Ha |
| 8. | Name of the Canal | Surauli canal |
| 9. | Discharge of Canal | 1.9 m3/s |
| 10. | Length of Canal | 14.80 km |
Table 1: Details of Arjun Sahayak Project.
There may be several alignments between the source of the canal and its destination. Each canal alignment has a different cost associated with it. In the present research, the cost function depends upon the cost of earthwork in filling and cost of earthwork in cutting. Each alignment has been divided into segments of 100 m each and the cost of earthwork has been computed for each segment. The total cost of earthwork was obtained by summing-up the cost of each segment. For each alignment the objective is to find the minimum combined cost of earthwork in filling and cutting. For each alignment, the computations of area and volume for a given topography have been completed using ESurveyCAD software. ESurveyCAD has the capability to provide a comprehensive software solution, enabling swift generation of contours, create sections for volume calculations, perform earthwork quantity assessments, and transforms point data into topographical maps. The ESurveyCAD earthwork module allows generating instant volume calculation and section drawings from the point data available in CAD drawings and levels available in Excel or CSV files. ESurveyCAD also allows generating earthwork reports during the progress of the projects and save time for quantity calculation. Its main features include the following: (1) Import data from CSV, Excel or CAD for earthwork calculation and section drawings. (2) Generates earthwork calculation with fixed formation level or between two surfaces. (3) Automatic calculations of optimum fixed formation level. (4) Generate volume reports for cutting and filling depending on depth of cutting height of the filling [15].
To quantify the financial implications of the earthwork, unit costs to excavation and embankment activities based on prevailing industry rates. The product of the volume of material and unit costs provided an estimate of the cost associated with cutting and filling for each alignment. The volumes have been computed using the division of square method. Upon completing the cost analysis, we have generated a comprehensive overview of the alignment options in terms of the associated cost graph. The alignments have been ranked based on their total cost, considering both cutting and filling expenses [16 ].
Results and Discussions
The four different alignments were investigated in the present research, and grid search technique was used to find the most optimal alignment. The topography of the area is a major factor that impacts the cost of excavation. Some segments of the canal may be in full cutting (Figure 2) while others may be in full filling (Figure 3). It is also possible that some segments are in partial cutting and partial filling (Figure 4).
Determination of the earthwork volumes in cutting and filling is primarily based on the topography of the area. The key objective is to identify the canal alignment that minimizes the combined cost of earthwork in filling and cutting. Numerous potential alignments may exist between the source and destination of the canal, but the focus is on achieving cost minimization.
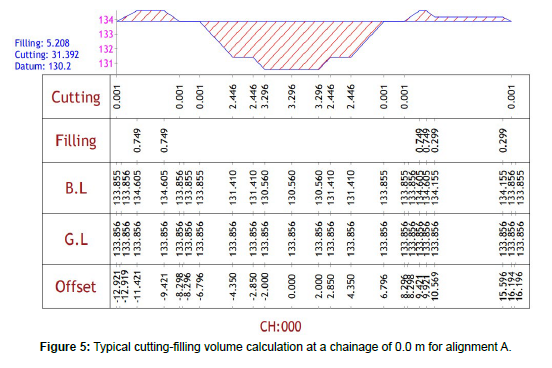
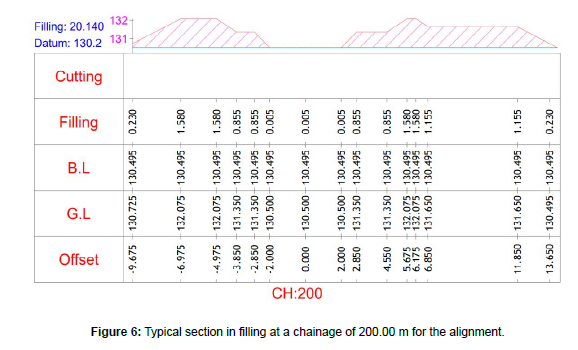
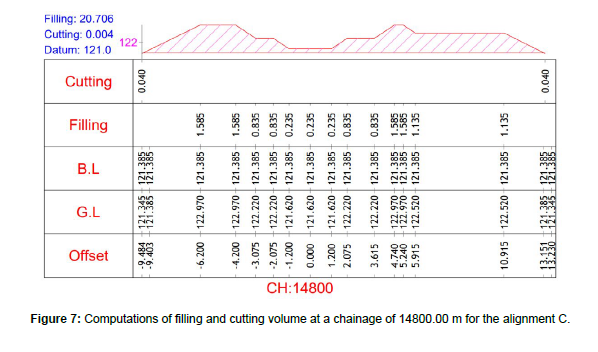
A section in partial filling and cutting for alignment A, along with the volume of earthwork in cutting and filling is shown in Figure 5. Chainage in Figure 5 refers to the precise measurement of distance along the central axis of a roadway or highway, typically expressed in meters or kilometers. This measurement is needed to accurately locate salient features, elements, or alterations along the alignment of the road. At a specific chainage, a cross-section offers detailed description of the configuration of the road, encompassing details of the road surface, shoulders, medians, ditches, embankments, and structures such as culverts and bridges. The computations for a typical section in full filling for the alignment B are shown in Figure 6. A partial filling and cutting section and the volume computations at a chainage of 14800.00 m for the alignment C are shown in Figure 7. A typical section in full filling at a chainage of 10000.00 m for the alignment D and the associated volume computations are shown in Figure 8.
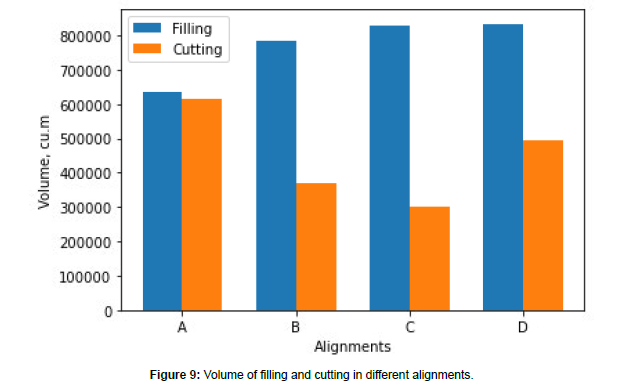
The total volume in filling and cutting and the total cost of excavation for different alignments have been shown in Table 2. Cutting involves the excavation or removal of soil, rock, or any other unwanted materials from the ground to create a depression in the ground. Filling, on the other hand, involves adding soil, rock, or other materials to create an embankment at a higher elevation. The computation of the filling and cutting volume involves computing the cross- sectional area of the cut at each point and then integrating these areas along the length of the alignment. To compute the cost of filling, the filling volume is multiplied by the unit rate. The unit cost of cutting and filling activities depends on several factors, including labor, equipment, and material hauling, disposal, and site conditions. The actual unit costs can vary widely based on location, project size, local regulations, and other variables. In the present research, the unit cost has been considered based on the prevailing market rates. The cost of cutting is obtained by multiplying the total cutting volume by the unit cost of cutting. The comparison of the total cutting volume and total filling volume for alignments, A, B, C and D has been presented in Figure 9.
Alignment |
Volume in cutting, m3 | Cost of Cutting in Million Rs. | Volume in filling m3 | Cost of filling in Million Rs. | Total volume of cutting and filling, m3 | Total cost of cutting and filling in Million Rs |
|---|---|---|---|---|---|---|
| A | 634237.95 | 101.47807 | 616957.85 | 160.40904 | 125.11958 | 261.88711 |
| B | 782342.85 | 125.17486 | 370143.55 | 96.23732 | 115.24864 | 221.41218 |
| C | 829314.75 | 132.69036 | 299771.3 | 77.94054 | 112.908605 | 210.6309 |
| D | 833469.7 | 133.35515 | 492348.05 | 128.01049 | 132.581775 | 261.36565 |
Table 2: Total volume and total cost computations for different alignments.
Figure 10 shows the cost of earthwork in filling and cutting for four different alignments labeled A, B, C, and D. It can be seen from Figure 10 that alignment A has a higher cost for filling than for cutting. Alignment B has almost identical costs for both filling and cutting. The cost for cutting is considerably higher than the cost of filling for alignment C. Alignment D also has a higher cost for filling compared to cutting. In terms of overall cost (both filling and cutting combined), alignment A is the most expensive. While each alignment has varied costs of filling and cutting, it is the combined cost of filling and cutting that is most important. Figure 11 shows the total cost of excavation (in Million Rs.) associated with four different alignments labeled A, B, C, and D.
It can be seen from Figure 11 that alignments A and D have almost identical costs, with alignment A being slightly expensive than alignment D. Both alignments have costs exceeding Rs. 250 Million. The cost of alignment B lies between the costs of alignments A and D. The optimal alignment is alignment C with a total cost of Rs. 220.6309 Million. In conclusion, alignment C comes out to be the most economical choice, while alignments A and D are the most expensive. Alignment B offers a middle-ground option in terms of cost.
Conclusion
Designing irrigation channels is an exercise that requires a holistic approach. The process involves several engineering aspects and encompasses considerations related to economics, environmental responsibility, and long-term agricultural sustainability. Optimization techniques are applied to ensure that the design not only meets the technical requirements but also maximizes efficiency and costeffectiveness. It is well acknowledged that well-planned irrigation channel designs have the potential to contribute to the prosperity of farmers. Efficiently optimizing the alignment of irrigation channels plays a critical role in ensuring the effective distribution of water while considering the cost of earthwork in cutting and filling. In this research, a methodology was introduced to determine the most optimal canal alignment for a real-world irrigation project in the Mahoba district of Uttar Pradesh, India. The computations of earth work, in filling and cutting, for four different alignments were made with the help of ESurveyCAD software. The feasibility of the application of the methodology presented herein to other projects has been adequately demonstrated. Through application of the methodology proposed herein, significant savings in the cost of medium to large scale irrigation projects can be achieved. Importantly, the methodology presented here is generic in nature and can be employed with minimal modifications to identify optimal canal alignments for various canal systems. The results of our study highlight the importance of choosing the right canal alignment to minimize cost of earthwork, ultimately contributing to the economic sustainability of irrigation projects. The detailed cost analyses provided for each alignment allow decision-makers to make informed choices based on both cost-effectiveness and alignment suitability.
References
- Bhattacharjya RK, Satish MG (2007) Optimal design of a stable trapezoidal channel section using hybrid optimization techniques. Journal of irrigation and drainage engineering 133: 323-329.
- Chahar BR (2005) Optimal design of parabolic canal section. Journal of Irrigation and Drainage Engineering, 131: 546-554.
- El-Molla DA, El-Molla MA (2021) Reducing the conveyance losses in trapezoidal canals using compacted earth lining. Ain Shams Engineering Journal 12: 2453-2463.
- Fan Y, Chen H, Gao Z, Chang X (2023) Canal water distribution optimization model based on water supply conditions. Computers and Electronics in Agriculture 205: 107565.
- Farzin S, Valikhan Anaraki M (2021) Optimal construction of an open channel by considering different conditions and uncertainty: application of evolutionary methods. Engineering Optimization 53: 1173-1191.
- Froehlich DC (1994) Width and depth-constrained best trapezoidal section. Journal of Irrigation and Drainage Engineering, 120: 828-835.
- Guo S, Shi Y (2018) Infrastructure investment in China: A model of local government choice under land financing. Journal of Asian Economics 56: 24-35.
- Kacimov AR (1992) Seepage optimization for trapezoidal channels. J Irrig Drain Eng 118: 520-526.
- Kentli AYKUT, Mercan O (2014) Application of different algorithms to optimal design of canal sections. Journal of applied research and technology 12: 762-768.
- Loganathan G V (1991) Optimal design of parabolic canals. Journal of Irrigation and Drainage Engineering, 117: 716-735.
- Rehman A, Sharif M, Shakeel M (2021) Influence of Pacific and Indian Ocean Temperatures on Monsoonal Rainfall in India. J Earth Sci Clim Change 12: 566.
- Allen RG, Clemmens AJ, Burt CM, Solomon K, O’Halloran T (2005). Prediction accuracy for projectwide evapotranspiration using crop coefficients and reference evapotranspiration. Journal of irrigation and drainage engineering 131: 24-36.
- Swamee PK, Chahar BR (2013) Optimal alignment of a canal route. In Proceedings of the Institution of Civil Engineers-Water Management 166: 422-431. Thomas Telford Ltd.
- Swamee PK, Mishra GC, Chahar BR (2000) Design of minimum seepage loss canal sections. J Irrig Drain Eng 126: 28-32.
- Swamee PK, Mishra GC, Chahar BR (2001) Design of minimum earthwork cost canal sections. Water resources management 15:17-30.
- Zhang F, He C, Yaqiong F, Hao X, Kang S (2022) Canal delivery and irrigation scheduling optimization based on crop water demand. Agricultural Water Management 260: 107245.
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Indexed at, Google Scholar, Crossref
Citation: Singh C, Sharif M (2023) Identification of Optimal Canal Alignment for aReal-World Canal in India. J Earth Sci Clim Change, 14: 736.
Copyright: © 2023 Singh C, et al. This is an open-access article distributed underthe terms of the Creative Commons Attribution License, which permits unrestricteduse, distribution, and reproduction in any medium, provided the original author andsource are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Usage
- Total views: 1955
- [From(publication date): 0-2023 - Dec 02, 2025]
- Breakdown by view type
- HTML page views: 1601
- PDF downloads: 354