Short Communication Open Access
How the Roadway Pavement Roughness Impacts Vehicle Emissions?
Fengxiang Qiao, Qing Li* and Lei YuInnovative Transportation Research Institute, Texas Southern University, Houston, Texas, 77004, USA
- Corresponding Author:
- Qing Li
Post-doctoral Fellow
Innovative Transportation Research Institute
Texas Southern University
3100 Cleburne Street, Houston, Texas, 77004
Tel: 713-313-7532
E-mail: liq@tsu.edu
Received date: July 14, 2017; Accepted date: July 21, 2017; Published date: July 26, 2017
Citation: Qiao F, Li Q, Yu L (2017) How the Roadway Pavement Roughness Impacts Vehicle Emissions? Environ Pollut Climate Change 1:134. 10.4172/2573- 458X.1000134
Copyright: © 2017 Qiao F, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Environment Pollution and Climate Change
Abstract
Understanding the environmental impacts of roadway management strategies is essential not only to the estimation of construction cost, but also the protection of the environment and the conservation of the global ecological system. Vehicle speed and fuel consumptions may vary with driving conditions. Vehicle emissions can be estimated based on the speed, acceleration rate, and Vehicle Specific Power (VSP), which could normally be listed in an Operating Mode Identification (OMID) table. The relationships between pavement roughness (indicated by International Roughness Index or IRI) and speed/fuel consumption could be reflected by linear models, while the IRI is nonlinearly correlated to the emissions. It is recommended further identifying the relationships between IRI and emissions with more on-road tests for all types of vehicles on different types of roadway systems, so as to minimize the environmental, ecological, and even public health impacts through proper roadway management strategies.
Keywords
Vehicle emissions; Environmental impacts; Public health impacts; Roadway pavement; Transportation infrastructure management
Introduction
Minimizing the environmental impacts of roadway construction and maintenance is essential to comprehensive design, planning and management of roadway infrastructure system for the optimistic goals of balanced sustainability, mobility, and safety. The vehicle emission related environmental costs during roadway pavement management are influenced by pavement-surface type, pavement condition, roadway geometrics, weather, temperature, vehicle operation speed, and so on.
The life cycle assessment (LCA) is normally used to evaluate air pollution from vehicle exhaust and the energy consumption under different pavement management strategies [1]. The major pollutants emitted from motor vehicles mainly include volatile organic compounds (VOC), carbon monoxide (CO), and nitrogen oxides (NOx), which have several adverse health effects on human lives and even the global environment. As long term pavement conditions deteriorate, road roughness increases and predictions based on fuel consumption and therefore vehicle emissions will increase. It is therefore very important to understand the relations between pavement roughness and vehicle emissions.
Pavement Roughness and its Relationships with Vehicle Speed
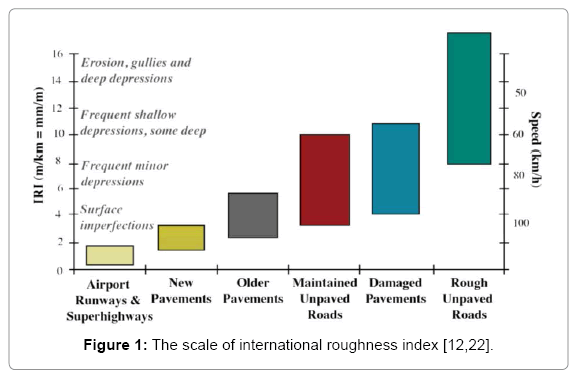
The pavement roughness, which is also called “smoothness”, is the deviation of a pavement surface from a true planar surface, with wavelength deviations ranging between 0.5 and 50 m [2]. The World Bank defines the pavement roughness using the so-called International Roughness Index (IRI), which is now in worldwide use [3] (Figure 1).
Pavement roughness affects vehicle speeds after maintenance and rehabilitation (M&R) activities [4-6], even though several studies did not report out such change [1,7-9] under certain conditions.
An early study [10] observed the increases in the mean speed after resurfacing: 2 km/h for private cars, 2.3 km/h for light goods vehicles, 2 km/h for medium goods vehicles and 2.6 km/h for heavy goods vehicles. Anund [11] investigated the relationship between surface quality (in IRI) and vehicle speed. The results showed that there was a statistically significant speed reduction of 1.6 km/h for passenger cars between 3.00 p.m. and 9.00 a.m. if the rut depth increased by 10 mm and a reduction of 2.2 km/h for an increase of one IRI.
Fuel Consumption Model and Cost Function Considering Pavement Roughness
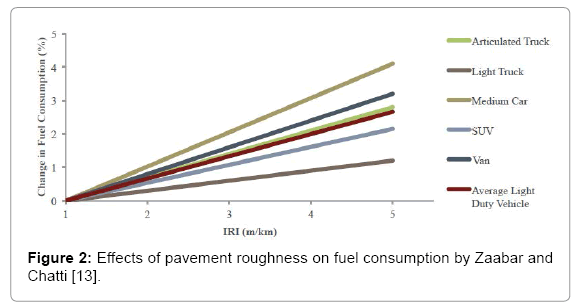
While the pavement condition affects the vehicle travel speed, it further affects fuel consumption and vehicle emissions. Rougher roads will lead to greater fuel consumption [12] and stiffer pavements could reduce fuel consumption up to 3 percent for the U.S. pavement network with a savings of 273 million barrels crude oil per year, and an annual decrease in CO2 emissions of 46.5 million metric tons (CSHUB) (2014). Various models have been developed to quantify fuel consumption based on the operational speed. The World Bank’s Highway Design and Maintenance Standards Model (HDM) is one such model, considering for the impact of pavement vehicle interaction (PVI) as part of the rolling resistance forces. Zaabar and Chatti [13] calibrated the mechanistic HDM-IV model for vehicles in the United States, which is showing in Figure 2.
Ozbay et al. [14] developed emission function to estimate the quantity of pollutant generated by motor vehicles, where the cost function is the multiplication of the unit cost values of each pollutant by the amount of pollutant emitted. The emission cost model assumes that the amount of pollutant released during motor vehicle operation is proportional with the amount of fuel consumed in quadratic form in Equation (1).
F=0.0723-0.00312V+5.403×10-5 V2 (1)
where F is fuel consumption at cruising speed (gallons/mile) and V is average speed (miles/hour). The total air pollution cost Cair, for a one mile long link, with a traffic volume Q (vehicles/hour) is calculated in Equation (2).
Cair=Q(0.01094+0.2155F) (2)
where Cair is measured in dollars per mile per hour.
Vehicle Specific Power and Emission Rates of Operating Mode Bins
In another study, the Highway Economic Requirements System- State Version (HERS-ST) [15] defines the emissions of a single pollutant per vehicle-mile of travel according to different average speeds and roadway section types. A common variable used in vehicle emission simulation is Vehicle Specific Power (VSP), which is a function of vehicle speed and acceleration. VSP is defined as the instantaneous tractive power per unit vehicle mass. The main advantages of using VSP as an independent variable for studying the stabilized emissions of passenger cars and light-duty trucks are: it can be directly calculated from roadside measurements; it captures most dependence emissions on engine operating parameters; and the certification driving cycles are defined as a speed versus time trace and can also be specified in terms of VSP. The commonly used unit of VSP is Kw/Metric Ton. VSP distributions not only represent well the driving characteristics but also are highly correlated with the vehicle emission characteristics. VSP is calculated using Equation (3).
VSP=v×[1.1a+9.81×grade(%)+0.132]+0.000302v3 (3)
where V is the vehicle speed (m/s), a is the vehicle acceleration (m/ s2) and grade(%) is the vehicle vertical rise divided by slope length. The VSP-based emission modeling approaches have been used to quantify a vehicle’s emissions during its regular operations [16]. As shown in the formula above, vehicle emission is directly affected by the travel speed and acceleration. Table 1 illustrates details of the operating mode binning, where the Operating Mode Identification (OMID) refers to operating mode bins that represent braking, idling, and varying levels of the vehicle’s VSP and speed. The operating modes are broken down into 23 bins that range from 0 to 40. As shown in Table 1, bins 0 and 1 represent braking and idling. Bins 11 to 16 represent driving behavior with lower speeds. Bins 21 to 30 represent driving behavior between 25 mph to 50 mph. Bins 33 to 40 represent driving behavior with speed 50 mph and greater.
| Operating Mode ID | Operating Mode Description | Vehicle Specific Power, VSPt (kW/tonne) |
Vehicle Speed, vt (mph) |
Vehicle Acceleration, at (mph/s) |
|---|---|---|---|---|
| 0 | Braking | (at ≤ -2) or (at ≤ -1 and at-1 ≤ -1 and at-2 ≤ -1) |
||
| 1 | Idling | -1 ≤ vt<1 | ||
| 11 | Low Speed Coasting | VSPt<0 | 1 ≤ vt<25 | |
| 12 | Cruise/Acceleration | 0 ≤ VSPt<3 | 1 ≤ vt<25 | |
| 13 | Cruise/Acceleration | 3 ≤ VSPt<6 | 1 ≤ vt<25 | |
| 14 | Cruise/Acceleration | 6 ≤ VSPt<9 | 1 ≤ vt<25 | |
| 15 | Cruise/Acceleration | 9 ≤ VSPt<12 | 1 ≤ vt<25 | |
| 16 | Cruise/Acceleration | 12 ≤ VSPt | 1 ≤ vt<25 | |
| 21 | Moderate Speed Coasting | VSPt<0 | 25 ≤ vt<50 | |
| 22 | Cruise/Acceleration | 0 ≤ VSPt<3 | 25 ≤ vt<50 | |
| 23 | Cruise/Acceleration | 3 ≤ VSPt<6 | 25 ≤ vt<50 | |
| 24 | Cruise/Acceleration | 6 ≤ VSPt<9 | 25 ≤ vt<50 | |
| 25 | Cruise/Acceleration | 9 ≤ VSPt<12 | 25 ≤ vt<50 | |
| 27 | Cruise/Acceleration | 12 ≤ VSPt<18 | 25 ≤ vt<50 | |
| 28 | Cruise/Acceleration | 18 ≤ VSPt<24 | 25 ≤ vt<50 | |
| 29 | Cruise/Acceleration | 24 ≤ VSPt<30 | 25 ≤ vt<50 | |
| 30 | Cruise/Acceleration | 30 ≤ VSPt | 25 ≤ vt<50 | |
| 33 | Cruise/Acceleration | VSPt<6 | 50 ≤ vt | |
| 35 | Cruise/Acceleration | 6 ≤ VSPt<12 | 50 ≤ vt | |
| 37 | Cruise/Acceleration | 12 ≤ VSPt<18 | 50 ≤ vt | |
| 38 | Cruise/Acceleration | 18 ≤ VSPt<24 | 50 ≤ vt | |
| 39 | Cruise/Acceleration | 24 ≤ VSPt<30 | 50 ≤ vt | |
| 40 | Cruise/Acceleration | 30 ≤ VSPt | 50 ≤ vt |
Table 1: Operating mode characteristics [21].
Once VSP is determined, the vehicle emissions can be calculated based on the operating mode binning approach. Tao et al. [17] conducted a research study and determined the emission rates in each operating mode bin using the real emission data of one lightduty vehicle collected by a Portable Emission Measurement System (PEMS). Those emission rates are shown in Table 2. Therefore, the total emissions can be calculated by combining the emission rates in Table 2 and the operating mode bins. Emission indexes analyzed in this study were Carbon Monoxide (CO), Carbon Dioxide (CO2), Oxides of Nitrogen (NOx) and Hydrocarbons (HC). The specific values in Table 2 should vary if a different type of vehicle with different mileage and vehicle age are measured.
| Operating Mode Identification (OMID) | CO2 (g/s) | CO (mg/s) | HC (mg/s) | NOx (mg/s) |
|---|---|---|---|---|
| 0 | 0.89 | 1.83 | 0.85 | 1.3 |
| 1 | 0.75 | 0.84 | 1.04 | 1.71 |
| 11 | 1.08 | 3.9 | 1.49 | 1.3 |
| 12 | 1.84 | 8.19 | 2.77 | 2.38 |
| 13 | 3.44 | 22.41 | 4.24 | 3.97 |
| 14 | 4.6 | 22.04 | 7.04 | 5.72 |
| 15 | 5.67 | 23.11 | 7.51 | 9.92 |
| 16 | 6.83 | 32.4 | 2.72 | 18.25 |
| 21 | 1.25 | 2.57 | 1.38 | 1.93 |
| 22 | 1.97 | 3.51 | 3.94 | 2.36 |
| 23 | 2.83 | 6.65 | 4.72 | 4.59 |
| 24 | 3.92 | 9.31 | 3.51 | 6.55 |
| 25 | 4.87 | 9.65 | 3.39 | 10.49 |
| 27 | 6.3 | 12.51 | 5.31 | 20.28 |
| 28 | 7.41 | 11.17 | 9.26 | 31.05 |
| 29 | 7.89 | 11.35 | 14.09 | 35.42 |
| 30 | 5.17 | 13.74 | 2.35 | 11.5 |
| 33 | 2.46 | 4.11 | 1.64 | 3.47 |
| 35 | 4.56 | 9.25 | 1.92 | 7.11 |
| 37 | 5.68 | 10.51 | 4.24 | 13.05 |
| 38 | 6.64 | 9.82 | 3.98 | 18.99 |
| 39 | 7.44 | 18.68 | 5.66 | 28.62 |
| 40 | 5.20 | 9.03 | 4.74 | 13.09 |
Table 2: Emissions rates of operating mode bins [17].
Recent Studies on Pavement Roughness and Vehicle Emissions
Li et al. [18] found that, the pavement roughness can be specified into four categories in terms of the characteristics of emission factors. They used the average Normalized Emission Factor (ANEF) to describe such classification. The ANEFs are 0.051, 0.032, 0.030 and 0.039 at levels of (1) IRI between 0+ and 1.99 m/km (category A), (2) IRI between 1.99 and 3.21 m/km (category B), (3) IRI between 3.21 and 6 m/km (category C), and (4) IRI being greater than 6 m/km (category D). They found that, the pavement categories C and D would induce higher exhaust emissions, higher interior noise, and higher driving stress (measured by drivers’ higher heart rates), which should not be recommended in pavement management.
Recently, based on the on-road measured emission data on one dedicated light duty vehicle from the PEMS and the related pavement roughness information with a sampling interval of 5 m along more than 1,000 miles road tests in Texas, USA, Li et al. [19] developed several nonlinear models such as the K-nearest neighbors (K-NN) and Neural Network models, for four major exhaust emission indexes (CO2, CO, HC and NOx.) The estimated emissions from those identified models are highly correlated to the real measured values. This study revealed that the relationship between pavement roughness and emission factors is complicated and nonlinear. While the rougher pavement would result in higher emissions, but the very smooth pavement would also induce higher emissions. Such findings should however, be further verified through larger scale tests and modeling studies.
In another study reported by Li et al. [20], an on-board emission test from four light duty vehicles was conducted in year 2016 with 12 subjects driving along several weaving areas (with very frequent on- and off-ramp operations) along State Highway 288 in Houston, Texas, USA during weekdays’ peak and nonpeak hours. Speed, acceleration, IRI, second-by-second vehicle emissions from PEMS were recorded, while five feature selection algorithms were used to identify the importance of dependent variables for a Normalized Emission factor (NEF). The predictive power of the four data mining algorithm based emission models was tested by a 10-fold cross validation procedure. The bagged decision tree algorithm was finally selected to construct the exhaust emission model with 50 grown decision trees. The predicted NEFs are highly correlated to the observed NEFs for both training and validation datasets (R-values=0.91 and 0.90, respectively.) While those results were from the limited tests on four light-duty vehicle, a very promising nonlinear modeling possibility is illustrated in the connecting pavement roughness with vehicle emissions.
Summary and Recommendation
In this paper, the impacts of pavement roughness IRI on vehicle speed, fuel consumption, and vehicle emissions are scanned. With the change of driving conditions including pavement roughness, the vehicle speed, fuel consumption, and emissions may all change. While some use the linear model to characterize the relationships between speed (as well as fuel consumption) and IRI, the models to reflect the impacts of IRI on vehicle emissions are normally complicated and nonlinear. Based on recently studies, both very smooth and very rough pavement would be associated with higher emissions. However, such findings were based on the measurement from one dedicated vehicle. It is recommended further investigating the relationships between IRI and vehicle emissions through even large scale on-road measurement for all types of vehicles. Such relationships are highly related to not only the understanding of environmental cost of roadway management system, but also the health of the public and even the entire ecological system.
Acknowledgement
The authors acknowledge that this paper is supported in part by the National Science Foundation (NSF) under the grant #1137732. The opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the funding agencies.
References
- Wang T, Harvey J, Lea JD, Kim C (2013) Impact of pavement roughness on vehicle free-flow SPEED. UCPRC-TM-2013-04.
- Sandberg U, Ejsmont JA (2003) Tyre/road noise reference book. NCEJ 51: 348-348.
- Sayers MW (1995) On the calculation of international roughness index from longitudinal road profile. Transp Res Rec 1501: 1-12.
- Kean AJ, Harley RA, Kendall GR (2003) Effects of vehicle speed and engine load on motor vehicle emissions. Environ Sci Technol 37: 3739–3746.
- Zhang H, Lepech MD, Keoleian GA, Qian SZ, Li VC (2010) Dynamic life-cycle modeling of pavement overlay systems: Capturing the impacts of users, construction and roadway deterioration. Journal of Infrastructure Systems 16: 299-309.
- Yu B, Lu Q (2012) Life cycle assessment of pavement: Methodology and case study. Transportation Research Part D: Transport and Environment 17: 380-388.
- Santero NJ, Horvath A (2009) Global warming potential of pavements. Environ Res Lett 4: 1-7.
- Wang T, Lee IS, Kendall A, Harvey J, Lee EB, et al. (2012) Life cycle energy consumption and GHG emission from pavement rehabilitation with different rolling resistance. J Clean Prod 33: 86-96.
- Lidicker J, Sathaye N, Madanat S, Horvath A (2013) Pavement Resurfacing Policy for Minimization of Life-Cycle Costs and Greenhouse Gas Emissions. JIS 19: 129-137.
- Cooper DR, Jordan PG, Young JC (1980) The effect on traffic speeds of resurfacing a road (Supplementary Report, SR571). Wokingham: TRL.
- Concrete Sustainability HUB (CSHub) (2014) New developments in the debate on pavement-vehicle interaction: The impact of pavement design on fuel consumption. Massachusetts Institute of Technology.
- Greene S, Akbarian M, Ulm FJ, Gregory J (2013) Pavement roughness and fuel consumption.
- Zaabar I, Chatti K (2010) Calibration of HDM-4 models for estimating the effect of pavement roughness on fuel consumption for U.S. conditions. Journal of the Transportation Research Board, pp: 105-116.
- Ozbay K, Bartin B, Berechman J (2001) Estimation and evaluation of full marginal costs of highway transportation in New Jersey. Journal of Transportation and Statistics 4: 81-103.
- Federal Highway Administration (FHWA) (2005) Highway economic requirements system – State Version Technical Report, Washington D.C.
- Shi Q, Yu L (2011) Evaluation of mobile source greenhouse gas emissions for assessment of traffic management strategies.
- Tao F, Yu L (2012) Effects of driving behavior on vehicle emission: A case study in Houston, Texas. In TRB 91st Annual Meeting Compendium of Papers DVD, No 0852, Transportation Research Board of the National Academies, Washington, D.C.
- Li Q, Qiao F, Yu L (2016) Clustering pavement roughness based on the impacts on vehicle emissions and public health. Ergonomics 6: 1-4.
- Li Q, Qiao F, Yu L (2017a) Non-linear models of light-duty vehicle emission factors considering pavement roughness. J Civil Environ Eng 7: 7: 268.
- Li Q, Qiao F, Yu L, Chen S, Li T (2017b) Impact of freeway weaving segment design on light-duty vehicle exhaust emissions. J Air Waste Manag Assoc.
- EPA (2011) Development of emission rates for light-duty vehicles in the motor vehicle emissions simulator (MOVES2010), Final Report EPA-420-R-11-011, U.S. Environmental Protection Agency.
- Sayers MW, Gillespie TD, Paterson WDO (1986) Guidelines for the conduct and calibration of road roughness measurements. World Bank Technical Paper Washington, DC, The World Bank. No. 46.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 4484
- [From(publication date):
July-2017 - Apr 04, 2025] - Breakdown by view type
- HTML page views : 3537
- PDF downloads : 947