Journal of Infectious Diseases & Therapy
Open Access

The COVID-19 (SARS-CoV-2) pandemic has caused more than 5 million casualties during the years 2020-2021, despite huge global efforts to dampen the spread of the virus [1]. Several vaccines have been developed and more than 9 billion vaccine doses have already been distributed [1]. Unfortunately the virus is gradually evolving, resulting in new COVID-19 variants under monitoring (VUM), Variants of Interest (VOI) and variants of concern (VOC), including the Alpha (B.1.1.7), Beta (B.1.351), Gamma (P.1), Delta (B.1.617.2) and Omicron (B.1.1.529) variants. These variants have higher basic reproduction number (R₀) and higher resistance against today’s vaccines as compared to the original COVID-19 virus.

Governments and other authorities all around the world are constantly trying to identify ideal strategies for counteracting the pandemic with minimal impact on health and economy. The aim of this study was to utilize an improved generic epidemiological equilibrium transmission model (with empirical input data) to predict required vaccination rates and restriction strengths for controlling different COVID-19 variants, including the Delta and Omicron variants. The model results can be used to optimize the preventive measures against COVID-19 variants.

Compartmental models, like the SIR (Susceptible, Infectious or Recovered) model [2], are used in epidemiology to capture timedependent phenomena, but the aim of this study is only to capture steady-state properties. Therefore, the mathematical model in this study was instead based on a well-known epidemiological equilibrium equation [3].

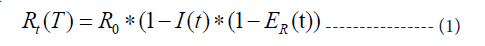
where Rt(t) is the time-dependent reproduction ratio at time t, R₀ is the initial reproduction ratio without restrictions, I(t) is the relative proportion of the population that is immune to the disease, and E_R(t) is the relative efficiency of all preventive measures against the spread (e.g. social distancing, increased hygiene rules, face-masks, quarantines etc.). Both I(t) and E_R(t) are limited to the interval 0 to 1. For I(t), 0 and 1 correspond to no immunity and complete immunity in the population,respectively. For E_R(t), 0 and 1 correspond to no preventive measures and complete isolation of every single individual in the population, respectively.

In this study, it was assumed that I(t) equals the fraction of vaccinated persons ϕ_v(t) times the average vaccine efficiency E_v(t), plus the fraction of recovered (non-vaccinated) persons ϕ_r(t) times the average preventive effect of recovering E_r(t):

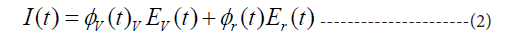
Typically, E_r(t) and E_v(t) decreases with time, whereas ϕ_r(t) and ϕ_v(t) gradually increases. In practice, several COVID variants and vaccines with different E_v(t)-values often co-exist, but for visualization and prediction purposes it is favorable to focus on one at the time. For simplicity and for pedagogical reasons, we counterfactually also assume that Er=Ev even though Er in reality often is higher than Ev, especially after longer periods of time. This assumption gives ϕ=ϕ_v+ϕ_r, resulting in:

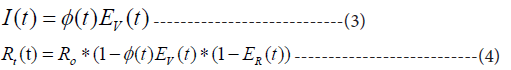
The condition for a decreasing infection rate is R_t(t)<1 and the equilibrium level is R_t(t)=1. If the latter condition is inserted in Equation 4, the equation for the required equilibrium fraction of vaccinated and recovered person’s ϕ_Eq becomes:

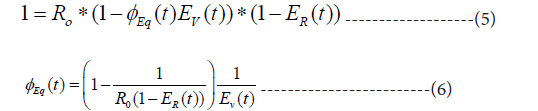
This relatively uncomplicated expression is useful for rapidly predicting the required fraction of vaccination in a population, both for COVID-19 and other pandemic infections. Since the model uses an average R-number for the whole population, it is conservative and rather overestimates than underestimates the required vaccination rates [1]. (People with many contacts typically become infected early in a pandemic, which lead to overestimated average transmission coefficients.)

As complement and validation for the modeling, data for COVID-19 incidence as function of vaccination fraction was collected from public sources for different European countries and regions 19-26 November 2021.

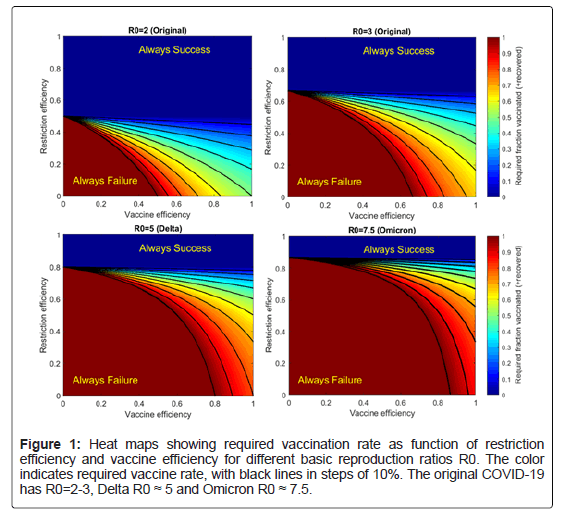
To predict how large fraction of the population that must be vaccinated and how strong restrictions that must be maintained to cease the pandemic, Equation 6 was plotted as function of basic reproduction number R₀, vaccine efficacy, and restriction efficiency (Figure 1).

Figure 1: Heat maps showing required vaccination rate as function of restriction efficiency and vaccine efficiency for different basic reproduction ratios R₀. The color indicates required vaccine rate, with black lines in steps of 10%. The original COVID-19 has R₀=2-3, Delta R0 ≈ 5 and Omicron R₀ ≈ 7.5.

The original COVID-19 virus has R₀ around 2-3 [4,5], Delta R₀ ≈ 5 [5] and Omicron R₀ ≈ 7.5 [5,6]. The basic reproduction number increases with increasing population density, and it becomes higher during the winter (on the northern hemisphere), probably because of lower humidity, less sunshine and more indoor activities.

The efficiency of today’s vaccines is lower against Omicron than against Delta and the ancestral COVID-19 virus. For Pfizer (BNT162b2), the efficacy is 88.2% and 88.0% against Delta and Omicron, respectively, 2-9 weeks after dose 2 [7]. The efficacy drops to 64.8% and 36%, 20-24 weeks after dose 2. A third dose increases the efficacy (after 2 weeks) to 92.6% and 75.5%, respectively. Similar trends were found for AstraZeneca (ChAdOx1-S with BNT162b2 booster-dose) [7] and Moderna (mRNA-1273) [8] and 75.5%, respectively. Similar trends were found for AstraZeneca (ChAdOx1-S with BNT162b2 boosterdose) [7] and Moderna (mRNA-1273) [8]. For the original COVID-19 variant, with basic reproduction number R₀ around 2-3 and a vaccine efficiency around 80-90% (2 doses), Figure 1 indicates that mediumstrong restrictions (50-70%) or a vaccination rate around 70% is sufficient to halt the pandemic. This has been confirmed empirically in many countries, both for the original COVID-19 virus and e.g., for the Alpha (B.1.1.7) and Beta (B.1.351) variants of concern.

For the Delta version, with R₀ ≈ 5 and vaccine efficiency around 65%-90% (2 doses), very high vaccination rates (~ 90%), very strong restrictions (80%), or a combination of medium high restrictions (50%-60%) and vaccination rates (70%) are required. This prediction is confirmed e.g., by the observation that the partial lockdown in Germany December 2021 succeeded to stop the Delta wave under these conditions.

For the Omicron version, with R₀ ≈ 7.5 and vaccine efficiency around 0%-88% (2 doses) or 54.6%-75.5% (3 doses), extremely strong restrictions (90%) or a combination of strong restrictions (70%-80%) and a high vaccination rate with three doses (70%-85%) is required.

Note that the required vaccination rate in Figure 1 is the combined fraction of vaccinated or recovered persons. Even if the vaccination/ restriction strategy fails, the transmission will stop when enough people have been infected and recovered, but to a larger cost in human lives and suffering. A high vaccination rate is strongly desired because it reduces both the virus transmission and the risk for serious health effects for the infected individuals. Although the hospitalization probability for Omicron is 40%-45% lower than for Delta, it is still high [9].

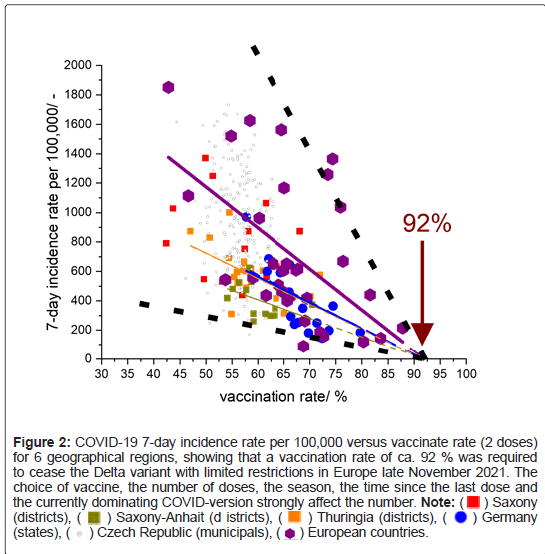
To confirm the modeling results, data for COVID-19 incidence and vaccination rate was collected 19-26 November 2021 for countries in Europe and regions in Germany and the Czech Republic. Data was mainly retrieved before the partial lockdown in Germany, which started 24th November. The 7-incidence (per 100 000) clearly decreased with increasing vaccination rate (Figure 2). A triangular pattern is evident, indicated by two enveloping black dashed lines. The logic behind these lines is that each country, city, or region has a specific reporting/testing procedure, resulting in different degrees of underreporting. Therefore, a huge scatter is evident for low or moderate vaccination rates. When approaching a specific rate of vaccination, the scatter must be smaller and reach (almost) zero. Thus, the two dashed lines must have a common intersection with the x-axis, and this point is the required vaccination rate to halt the pandemic.

Figure 2: COVID-19 7-day incidence rate per 100,000 versus vaccinate rate (2 doses) for 6 geographical regions, showing that a vaccination rate of ca. 92 % was required to cease the Delta variant with limited restrictions in Europe late November 2021. The choice of vaccine, the number of doses, the season, the time since the last dose and the currently dominating COVID-version strongly affect the number. Note: ,

The data indicates that a vaccination rate around 92% (2 doses) would have been sufficient to suppress the pandemic in Europe late November 2021, without serious restrictions. At that time, the Delta (B.1.617.2) variant of concern was dominant. Since the required vaccination rate is affected by season, currently dominant Covid variant, typical vaccinetype [10], average time since the last dose, maximum number of doses etcetera, the value of 92% is obviously not generally applicable. In December 2021, during the partial lockdown in Germany, the German incidence decreased, indicating that those restrictions were sufficient to halt the Delta-virus at a vaccination level around 70% (2 doses). The currently dominating Omicron (B.1.1.529) variant of concern is however more infectious and requires stronger measures to quench. All these results agree with the modeling predictions.

An epidemiological equilibrium model was applied to predict required vaccination rate and/or required amounts of restrictions as function of (empirically known) vaccine efficiencies and basic reproduction numbers (R₀). The model indicates that for the Omicron (B.1.1.529) variant of concern, a combination of strong restrictions (70%-80%) and high vaccination rates (70-90%) with three doses of e.g. the Pfizer (BNT162b2) vaccine will be required; otherwise a large proportion of the population will be infected. Tailor-made updates of the vaccine will probably be needed to stop the pandemic completely without maintaining relatively severe restrictions or without accepting that large fractions of the population become infected. It is strongly recommended to rapidly encourage a high (3-dose) vaccination rate, because that will decrease both the virus transmission and the severity of the infections. For the Delta (B.1.617.2) variant of concern, our data (empirical and model predictions) indicate that a vaccination (and/or recovery) rate of ~ 92% (2 doses) is sufficient for stopping the pandemic without serious restrictions, under conditions like those in Europe late November 2021.

1. Ritchie H, Mathieu E, Rodés-Guirao L, Appel C, Giattino C (2020) Coronavirus pandemic (COVID-19). Our world in data.

   [Google Scholar]

2. Cooper I, Mondal A, Antonopoulos CG (2020) A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solit Fractals 139:110057.

   [Crossref] [Google Scholar] [PubMed]

3. Britton T, Trapman P, Ball F (2020) The risk for a new COVID-19 wave-and how it depends on $ R_0 $, the current immunity level and current restrictions. R Soc Open Sci

   [Crossref] [Google Scholar] [PubMed]

4. Hilton J, Keeling MJ (2020) Estimation of country-level basic reproductive ratios for novel Coronavirus (SARS-CoV-2/COVID-19) using synthetic contact matrices. PLoS Comput Biol 16:1008031.

   [Crossref] [Google Scholar] [PubMed]

5. Liu Y, Rocklöv J (2021) The reproductive number of the Delta variant of SARS-CoV-2 is far higher compared to the ancestral SARS-CoV-2 virus. J Travel Med.

   [Crossref] [Google Scholar] [PubMed]

6. Nishiura H, Ito K, Anzai A, Kobayashi T, Piantham C, et al. (2022) Relative Reproduction Number of SARS-CoV-2 Omicron Compared with Delta Variant in South Africa. J Clin Med 1:30.

   [Crossref] [Google Scholar] [PubMed]

7. Andrews N, Stowe J, Kirsebom F, Toffa S, Rickeard T, et al. Effectiveness of COVID-19 vaccines against the Omicron (B.1.1.529) variant of concern. medRxiv

   [Google Scholar]

8. Hansen CH, Schelde AB, Moustsen-Helms IR, Emborg HD, Krause TG, et al. (2021) Vaccine         effectiveness against SARS-CoV-2 infection with the Omicron or Delta variants following a two-dose or booster BNT162b2 or mRNA-1273 vaccination series: A Danish cohort study. medRXiv.

   [Crossref] [Google Scholar] [PubMed]

9. Ferguson N, Ghani A, Hinsley W, Volz E. Hospitalisation risk for Omicron cases in England. Imperial College London.

   [Crossref] [Google Scholar] [PubMed]

10. Katella K (2021) Things to Know About the Delta Variant Yale Medicine.