Review Article Open Access
Geometry and Proportion of Conical Domes' Plans in Iran: Reviewing Case Studies
Sepideh Korsavi* and Mohammad Aliabadi
Art and Architecture Faculty, Shiraz University, Iran
- *Corresponding Author:
- Sepideh Korsavi
Master Student, Art and architecture
faculty Shiraz University, Iran
Tel: +420 603 979 915
E-mail: Sepidehkorsavi@gmail.com
Received Date: August 07, 2014 Accepted Date: April 17, 2015 Published Date: April 27, 2015
Citation: Korsavi S, Aliabadi M (2015) Geometry and Proportion of Conical Domes' Plans in Iran: Reviewing Case Studies. J Archit Eng Tech 4:137. doi:10.4172/2168-9717.1000137
Copyright: © 2015 Korsavi S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Architectural Engineering Technology
Abstract
The aim of this paper is to identify descriptive and quantitative features of conical domes to introduce geometry and proportion of their plans through analytic reviewing of case studies. Since geometry and proportion have been studied in conical domes, plans of conical domes need more attention in terms of geometry and proportion. Authors hypothesized that with introducing a new Ratio, analyzing geometry would be possible. This Ratio revealed nearly the value of √2 or √3 which is one of the most important Ratios in Islamic architecture. Authors have presented diagrams of superimposed squares and circles to suggest principles of designing with such Ratios. All kinds of plans whether circles or polygons can be designed based on these diagrams since circle is the basic geometry in Islamic architecture. Studying conical domes is important since studies show that their construction has lasted until Qajari era and may continue despite advances in other kinds of domes. Such studies strengthen the connection between past and present architecture of Iranian architecture.
Keywords
Conical domes; Plan form; Ratio; Proportions; Geometry
Introduction
Islamic art favors geometry in general and geometrical proportion in particular which carry great importance in the design process of Islamic art [1]. Islamic architecture has long been known as the embodiment of mathematical and geometrical premises [2]. In an architectural monument all dimensions, both in its integrity (height, length and width) and in its components (including geometrical surface patterns), are interrelated and never divorced from geometry [3]. Geometry as science for selection of structural dimensions such as height, length and width of the building and its structural elements governs the structural behavior of the building, the behavior that follows the geometry. The right geometry makes the building behave correctly [3]. In Persian architecture, it is geometry that provides diverse stylistic developments for constructions and designs; not only to serve a function, but also to evoke an emotional response by harmonization of the constructional elements, such as domes and columns and decorative elements [1]. Seyyid Hossein Nasr argued that geometry and rhythm manifest a doctrine of unity which is central to Islam, upon which Islamic art developed based on mathematical ratios and proportions which represent the very heart of Islam [4].
On the other hand, geometry involves proportions and prime roots that are considered the most beautiful proportions (the proportions of beauty) [4]. Proportion in architecture can be said to be ‘‘an harmonious relationship between the parts, with and within the whole’’ [3]. In architecture, the role of the proportioning system is to create a set of visual relationships between all the different parts of a building, and between the parts and their whole. The aim is to provide a sense of order in the overall structure [4]. Geometrical analysis of many Persian historic buildings has proven that a complete knowledge of proportions was widely used in Persian architecture [5] and it was the basis of Persian aesthetics [3].
Regarding studies related to geometry and proportion of domes, some papers [2-4,6-16] are worth considering. As can be seen, much attention has been paid to geometry and proportion of domes and their patterns but not that much to geometry and proportion of Islamic plans [6], especially those of conical domes which have been ignored compared to other kinds of domes. Moreover, plans of conical domes are more likely to have special Ratios compared to pointed and bulbous domes mainly due to two reasons. First, technological and architectural advances has caused pointed and bulbous domes to be more various in geometry and proportion of plan forms. Second, pointed and bulbous domes have often been used in religious complexes than in single funerary buildings where the proportion and geometry of the whole complex becomes more important. In fact, such proportion may seem unique in the plans of conical domes. Authors hypothesized that having a Ratio in plans of conical domes does not seem inconceivable since geometry is apparent in other parts of these domes. We tend to examine the layout of these plans through samples to test our hypothesis. Accordingly, this paper is arranged into three parts: 1) studying descriptive information of case studies: morphology, plan form and their origin 2) Defining new Ratios based on quantitative features to test our hypothesis 3) introducing principles of drawing and designing.
Origin, History and Types of Conical Domes
Regarding the evolution of conical domes, double-shells are followed by one-shell domes and were mostly used due to climatic conditions like heavy raining [17]. Accordingly, these domes were first used in the north of Iran with such climatic conditions [18] to protect the internal shell from humidity [19]. Moreover, the interior shell could expose ornamentations with its proportionate dimension and the exterior shell could be designed higher to add significance to the building [19]. The triple-shell demonstrates the advancement of structural design by adding a third shell to enhance its stability [8]. The third shell provides more resistance against forces [20]. In the conical roof (shell) cases, stone slabs or brick layers rested on the lower roof (shell) with some internal voids for reducing the weight and protecting the lower parts [7].
Regarding different eras, there are numerous innovative architectural contributions made during Seljuks among which is advancing the use of conical domes [21]. Some of the most enduring signs of Seljuk architecture are the distinct types of polyhedral and conical domes which still stand in Iran as seen in Figure 1. These edifices are commonly well-known as a primitive architectural formula for the Islamic funerary buildings topped with conical and polyhedral shells which mainly appeared in the Seljuk period [8] (Figure 1).
Figure 1: Case studies of Seljuks era. From left to right: Qabus dome [photo: 6]. Mehmandust [photo: http://ghiasabadi.com/pep/tower-of-mehmandust.html]. Toqrol [http://www.irantouronline.com/tehran/historical-places/toqrol-tower-ray.html]. Sorkh, Seh gonbad, Kabud [photo: http://en.wikigogo.org/en/168827/]. f) Damavand [photos:31].
During the Ilkhanid period, the construction of conical and polyhedral domes decreased considerably in comparison with the Seljuk era, but still there were two specific architectural achievements during this period, small brick connectors and extensive use of turquoise tile works as can be seen in Figure 2 [8].
The construction of conical and polyhedral domes became less important during the Timurid period due to two main reasons, by developing the use of pointed domes and with the introduction of the bulbous style [8]. It should be noted that these domes have also been built in hot-arid areas like Qom in this era. Its reason is mainly attributed to the fact that some great conical domes have been destroyed by sunnis1 in Ilkhanids era which lead to the usage of conical domes as the symbol of shias'2 buildings. That is why the usage of these domes became common in Qom and kashan after Ilkhani era without having any congruence with hot and dry climate of these cities [18]. Case studies of Timurids era show the emergence of polyhedral and pyramidal domes in religious complexes and hot-arid areas. Figure 3 shows case studies of Timurid era [22].
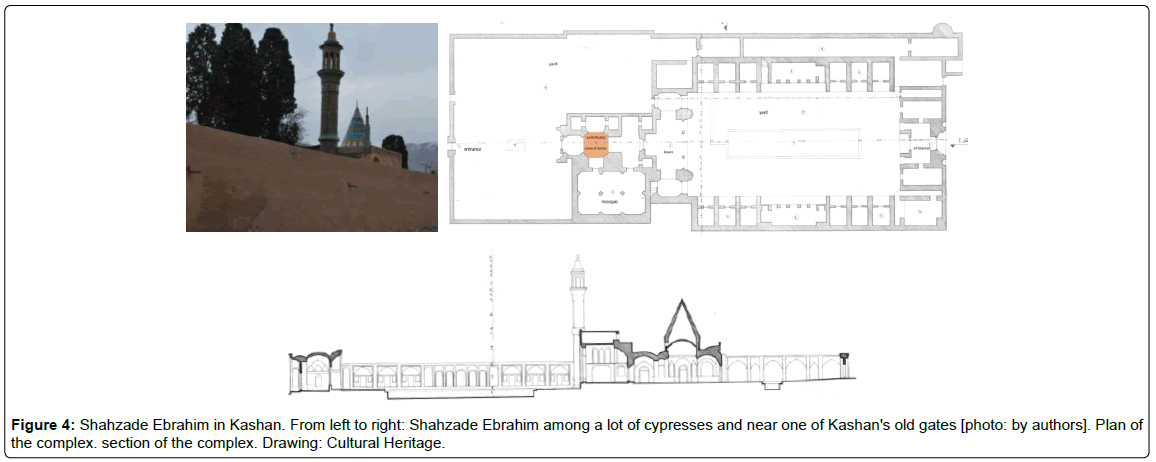
Still we can see the trace of these domes in different eras which surely shows their popularity among Muslims [23]. Another important point is that conical domes have appeared in religious complexes afterward and not as an individual funerary building. In some cases, the sanctuary's proportion can easily be addressed by conical domes and there is no need to construct domes with larger spans or heights. Shahzade Ebrahim in Kashan is among one of these complexes as can be seen below. This conical dome has been designed in a site with a lot of cypresses and near one of Kashan's old gates to attract attention when entering city. Therefore polyhedral dome is in complete agreement with required dimension, the shape of cypresses and location of the complex in city. That is why their construction continued in some cases even after Ilkhanids era (Figure 4).
Furthermore, the construction of conical domes have made progresses in following eras including the increased number of hedrons3 and increased height of drums as can be below Figure 5.
Case Studies' Information
Twenty-five samples of conical domes, which were built in Iran, were subjects of this analysis. Authors examine plans of conical domes to test their hypothesis. Tables 1 and 2 show the descriptive and quantitative features of case studies respectively. In Table 2, exterior diameter (E) shows either diameter of the circular plan or diameter of the circle that surrounds polygon or has been surrounded by polygon. Moreover, O Ratio (external to internal diameter Ratio) is introduced to reveal geometry and proportion of plans which is the purpose of this paper. M and N Ratios help show the overall form of conical domes. In Table 2, dimensions are based on plans acquired from different papers. These plans have been drawn and dimensioned again by authors to find out exact figures (Tables 1 and 2).
| Case Studies (Towers, Tombs, shrines) |
Place | Era | Plan | Parts | Ref | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Exterior Plan-(number of divisions) | Interior Plan | bench | Load Bearing System | Transition Tier | Drum | Shell | |||||
| Exterior Shell | Interior Shell | ||||||||||
| Qabus Dome | Gorgan | 1007 | circle- 10 | circle | no | cylinder | one shell and conical | 2 | |||
| Mehmandust | Damqan | 1097 | circle- 22 | circle | yes | cylinder | 31 | ||||
| Toqrol Tower | Rey | 1139 | circle- 24 | circle | yes | cylinder | conical | 31 | |||
| Surkh Dome | Maraqe | 1147 | Square | square | yes | Cubic | octagon | octagonal pyramid | semi-spherical | 6, 8, 31 | |
| SehGonbad | Oromie | 1180 | Circle | circle | yes | cylinder | conical | saucer | 6, 23, 31 | ||
| KabudGonbad | Maraqe | 1196 | Decagon | decagon | yes | decagonal prism | 10-sided prism | pyramid | 10, 31 | ||
| Damavand Tower | Damavand | Octagon | circle | yes | octagonal prism | octagonal pyramid | saucer | 31 | |||
| Above case studies are of Seljuks Era, 1038-1194 A.D | |||||||||||
| Allaeddin Tower | Varamin | 1289 | Circle | circle | no | cylinder | conical | semi-spherical | 2,5,23 | ||
| Sheikh abddolsamad | Natanz | 1325 | Square | no | octagonal prism | octagon | Octagonal prism | octagonal pyramid | saucer | 2,5,18 | |
| HamdollahMostofi | Qazvin | 1340 | Square | no | Cubic | octagon | cylinder | conical | semi-spherical | 5, 16 | |
| Khajeasilodin | Qom | 1340 | 12-sided | octagon | no | 12-sided prism | 16-sided prism | One shell and 16-sided pyramid | 2 | ||
| Ali ebnejafar | Qom | 1346 | Octagon | square | no | 12-sided prism | 12-sided pyramid | semi-spherical | 2 | ||
| Baba qasem | Esfahan | 1350-1400 | Square | square | no | Cubic | Octagonal prism | One shell and octagonal pyramid | 6 | ||
| Radkan tower | Radkan | 12-sided | octagon | no | cylinder | conical | semi-spherical | 28, 29 | |||
| Above case studies are of Ilkhanids Era, 1256-1353 A.D | |||||||||||
| Khajealisafi | Qom | 1398 | 12-sided | octagon | no | 12-sided prism | 16-sided prism | 16-sided pyramid | 2 | ||
| Abbas shrine | Qom | 1406 | Octagon | octagon | no | octagonal prism | octagon | octagonal pyramid | semi-spherical | 4 | |
| Ebrahim shrine | Qom | 1412 | Octagon | square | no | octagonal prism | 16-sided prism | 16-sided pyramid | semi-spherical | 2, 3 | |
| Shams tabarsi | Amol | 1427 | Square | square | no | Cubic | octagon | Square pyramid | 23, 34 | ||
| Qasem Shrine | Sari | 1466 | Circle | circle | no | Cylinder | 12-sided prism | decagonal pyramid | 4 | ||
| Zeinolabedin shrine | Sari | 1484 | Square | square | no | Cubic | octagon | octagonal pyramid | semi-spherical | 4, 16 | |
| BayazidBastami complex | Natanz | 1516 | Square | no | Cubic | cylinder | Triple-shell and conical | saucer | 5, 6 | ||
| Shomali tomb tower | Qom | Octagon | octagon | no | octagonal prism | 16-sided pyramid | 2 | ||||
| Above case studies are of Timurids Era, 1370-1510 A.D | |||||||||||
| Mirneshane Shrine | Kashan | 1583 | octagon | 12-sided | no | 16-sided prism | 16-sided pyramid | semi-spherical | 11 | ||
| Abulolo Tomb | Kashan | before Safavi | decagonal prism | 20-sided prism | 20-sided pyramid | authors | |||||
| ShahzadeEbrahim | Kashan | qajar | Part of a complex | 16-sided prism | 16-sided pyramid | saucer | authors | ||||
Table 1: Shows the descriptive features of case studies.
| Case Studies | Dimensions and Proportions | Plans- All plans' drawings: authors | Ref | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Height of Bench | Height | Interior diameter = I | Exterior diameter = E | N=Rise/span | M= H/E | O= E/I |  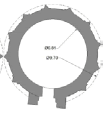 |
||
| Seljuks Era, 1038-1194 A.D | |||||||||
| Qabus Dome | 57 | 6.9 | 9.7 | 1.3 | 5.8 | ~1.40 | 2 | ||
| Mehmandust (right plan) |
1 | 14.5 | 6.8 | 9.7 | 1.49 | ~1.42 | 31 | ||
| Toqrol Tower | 21 | 10.3 | 14.8 | 1.418 | ~1.43 | 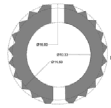 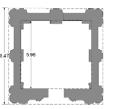 |
31 | ||
| SurkhGonbad (right plan) |
1.5 | 10 | 5.9 | 8.4 | 1.2 | ~1.42 | 6, 8, 31 | ||
| SehGonbad | 1.5 | 13 | 3.4 | 5 | 2.6 | ~1.45 | 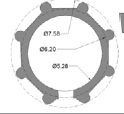 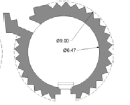 |
3, 23, 31 | |
| Kabud Dome (right plan) |
2.3 | 6.7 | 9.8 | ~1.46 | 10, 31 | ||||
| Damavand | 2 | 10 | 5.25 | 7.5 | 1.6 | ~1.44 | 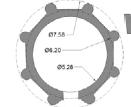 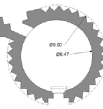 |
31 | |
| Ilkhanids Era, 1256-1353 A.D | |||||||||
| Allaeddin Tower (right plan) |
18 | 6.45 | 9 | 1 | 2 | ~1.40 | 2, 5, 23 | ||
| Khajeasilodin | 20 | 6.9 | 10 | 2 | ~1.44 |  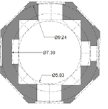 |
2 | ||
| Ali ebnejafar shrine (right plan) |
22.5 | 5.8 | 9.25 | 1 | 2.4 | ~1.59 | 2 | ||
| Radkan Tower | 25.6 | 8.5 | 12.7 | 0.75 | 2 | ~1.49 | 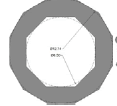 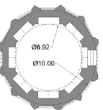 |
29, 28 | |
| Timurids Era, 1370-1510 A.D | |||||||||
| Khajealisafi (right plan) |
20 | 6.9 | 10 | 2 | ~1.44 | 2 | |||
| Abbas shrine | 20 | 8.9 | 13.3 | 1.5 | ~1.49 | 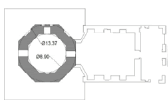 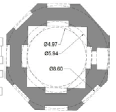 |
4 | ||
| Ebrahim shrine (right plan) |
14.6 | 5 | 8.6 | 1 | 1.70 | ~1.72 | 2, 3 | ||
| Shams tabarsi | 32 | 11.2 | 16.7 | 0.55 | 1.9 | ~1.49 | 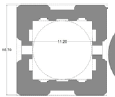 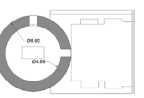 |
23, 35 | |
| Qasem Shrine (right plan) |
15 | 4.9 | 6.6 | 2.3 | ~1.35 | 4 | |||
| Zeinolabedin | 20 | 4.65 | 6.8 | 2.9 | ~1.46 | 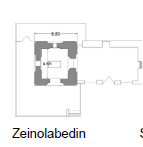 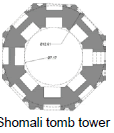 |
4, 16 | ||
| BayazidBastami complex | 20 | 8 | 1 | 2.5 | 5, 6 | ||||
| Shomali tomb tower | 12 | 7.1 | 12.6 | 0.95 | ~1.77 | 2 | |||
| Other eras | |||||||||
| Mirneshane | 20 | 7.3 | 10.2 | 1 | 2 | ~1.4 | 11 | ||
| ShahzadeEbrahim | 14 | 4.8 | 1.2 | 2.9 | Cultural heritage | ||||
Table 2: Shows the quantitative features of case studies.
Discussion
Regarding the variety of case studies, it can be realized that conical and polyhedral domes are so various and have different morphological features and plan forms in each era. Generally, Islamic domes present a wide variety of sizes and types, but some geometric properties were repeatedly used in their composition designs. Nevertheless, no two samples are exactly the same [7].
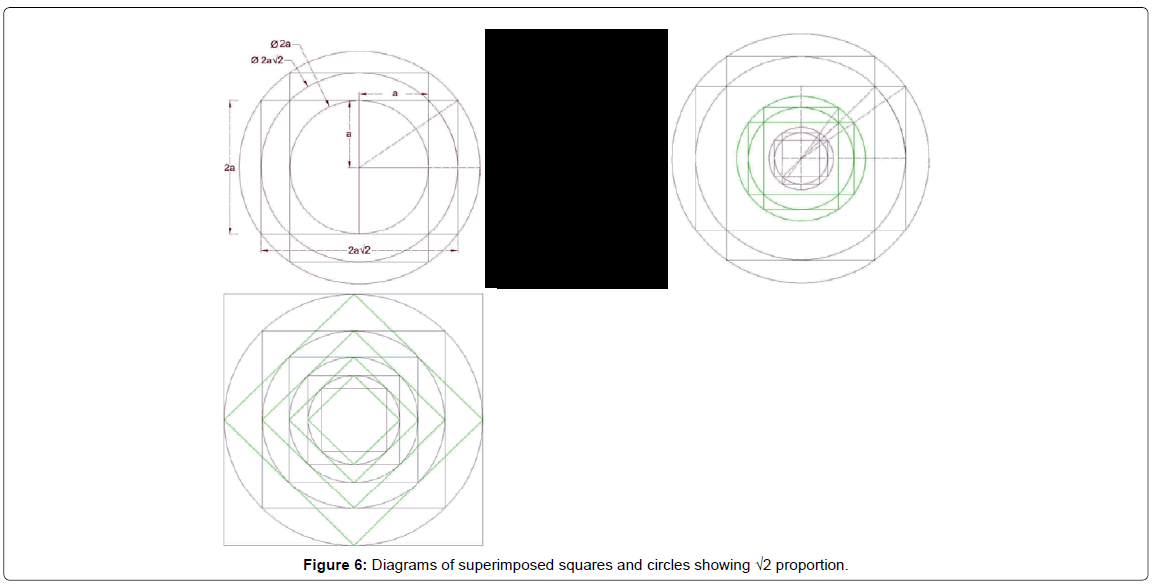
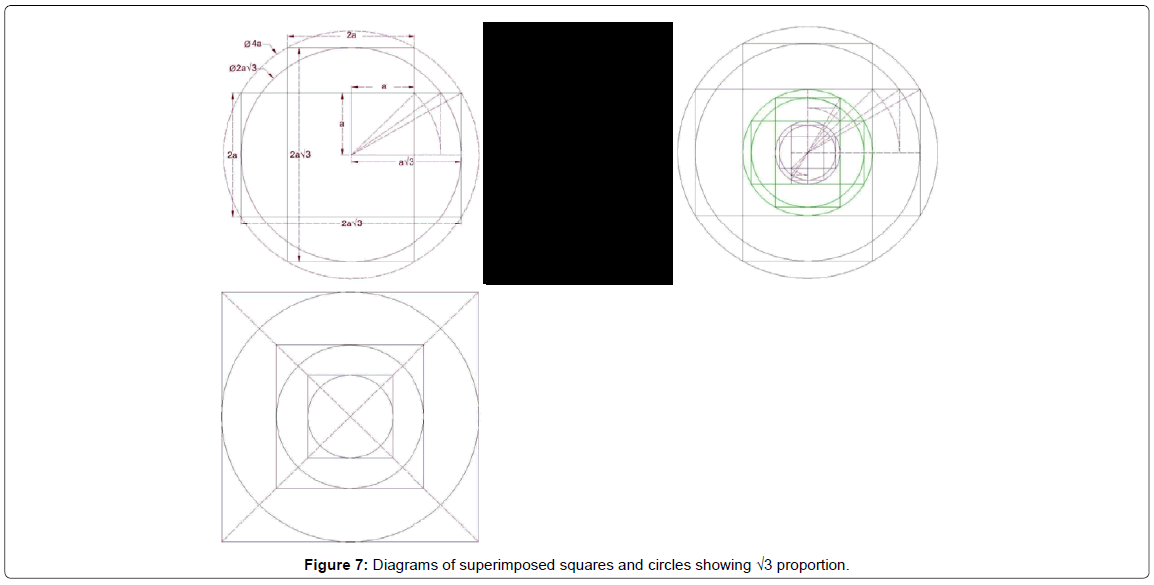
Through geometrical analysis of case studies, the authors have noticed the value near the √2 Ratio (with an approximation of less than 0.08) or in some cases the value near the √3 Ratio (with an approximation of less than 0.04) for plan's external diameter to internal diameter (O) for most case studies. In architecture dating back to prehistory, particularly in Islamic arts and architecture, the most important geometric proportional systems are: the proportions of the golden mean and the primary three proportional roots √2, √3 and √5, on which all Islamic arts and architectural forms, especially their geometric pattern design, are based [1]. The usage of √2 and √3 Ratio and modules in Iranian architecture in pre-Islamic era and Islamic era show an exact system of proportions which have been widely used [24]. These Ratios can be seen and followed in the below diagrams of superimposed squares and circles (Figures 6 and 7).
In the above diagrams, the circle plays a major role in defining and designing plans. The circle is an obvious example of a basic geometry, constituting all the proportional geometries inherent in traditional architecture. The circle of Unity is the most significant form, for it contains a circumference revolving around a fixed center. It is therefore extremely important to understand that all other geometric shapes can be determined from a circle, from which come the full polygons, including series of roots and proportions [1]. Some researchers stated that the use of the circle is a way of expressing the Unity of Islam. According to this doctrine, the circle and its center is the point at which all Islamic patterns begin [6]. Circular plan in Islamic architecture represents one of the most important aspects of life which is unity and perfection. Circle is the symbol of holiness and the only perfect figure able to express God' glory [25]. Squares, pentagons, octagons, decagons and all other polygons can be drawn based on surrounded or inscribed circles. That is why diagrams have been prepared based on circles and squares.
Having examined O Ratio, we turn to M and N Ratios. These two Ratios do not show any special relationship unless M Ratio reveals the fact that height to exterior diameter Ratio has increased to some extent over time. It shows a revolutionary process in the proportions of conical domes.
Conclusion
Conical, polyhedral and pyramidal domes are among distinct features of Iranian domes which play an important role in the development of tomb towers and shrines. In Iranian architecture [26], geometry and proportions provide developments for constructions and designs of conical domes. Through geometrical analysis of case studies, the authors have noticed the value near the √2 Ratio and √3 Ratio for plan's external diameter to internal diameter (O) for most case studies. This Ratio is the most important one since it reveals the form and dimensions of the plan. Diagrams have been presented showing these Ratios by superimposed squares and circles. Circle is the most significant form of these diagrams for its basic geometry. All samples' plans can be designed based on these diagrams.
Finally, it can be concluded that recalling mathematics and proportions to Iranian architecture [27-30] is of great importance and value for a better connection between past and present architecture. A comprehensive understanding of conical domes and their proportions can set the stage for standards which strengthen such a connection.
1Sunni: One of the two main branches of Islam, differing from shia in its acceptance of the first three caliphs.
2Shia: One of the two main branches of Islam, regarding Ali, the fourth caliph, as Muhammad's first true successor.
3Hedrons: Denoting geometrical solids having a specified number of plane faces or denoting geometrical solids having faces of a specified shape.
References
- Dabbour LM (2012) Geometric proportions: The underlying structure of design process for Islamic geometric patterns. Frontiers of Architectural Research1: 380-391.
- Sarhangi R (2012) Persian Architecture and Mathematics: An Overview. Nexus Network Journal14:197-201.
- SarhangiR (1999) The Sky Within: Mathematical Aesthetics of Persian Dome Interiors. Nexus Network Journal1: 87-98.
- Boussora K,MazouzS (2004) The use of the Golden Section in the Great Mosque at Kairouan. Nexus Network Journal6: 7-16.
- Qolamali H (2000) Islamic Iranian architecture in Seljuks era, Tehran
- Saoud R (2003) Muslim Architecture Under Seljuk Patronage, foundation for science technology and civilization.
- AbdullahiY, Embi MRB (2013)Evolution of Islamic geometric patterns. Frontiers of Architectural Research2: 243-251.
- Ashkan M, Ahmad Y (2010) Discontinuous Double Shell Domes through Islamic eras in the Middle East and Central Asia: History, Morphology, Typologies, geometry and Construction. Nexus Network Journal12 : 287-319.
- Ashkan M, Ahmad Y (2012) Significance of Conical and Polyhedral Domes in Persia and Surrounding Areas: Morphology, Typologies and Geometric Characteristics. Nexus Netw J14 : 275-290.
- Carol B(2012) The Decagonal Tomb Tower at Maragha and Its Architectural Context: Lines of Mathematical Thought. Nexus Netw J14: 251-273.
- Chorbachi WAK (1989) In the Tower of Babel: Beyond symmetry in islamic design. Computers & Mathematics with Applications17: 751-789.
- Cromwell PR, Beltrami E (2011)The whirling kites of Isfahan: geometric variations on a theme. The Mathematical Intelligencer33: 84-93.
- Hejazi M (2005) Geometry in nature and Persian architecture. Building and environment40: 1413-1427.
- Huerta S (2006) Galileo was wrong: the geometrical design of masonry arches. Nexus Network Journal8: 25-52.
- HuertaS (2007) Oval domes: History, geometry and mechanics. Nexus Network Journal9: 211-248.
- Kaplan CS, Salesin DH (2004) Islamic star patterns in absolute geometry. ACM Transactions on Graphics (TOG)23: 97-119.
- Mustafa FA, Hassan AS (2013) Mosque layout design: An analytical study of mosque layouts in the early Ottoman period. Frontiers of Architectural Research2: 445-456.
- MemarianQ(1988)Vaulted Sructures in Islamic Architecture of Iran. Elm o Sanat University, Tehran.
- Arab K (1994) Features of the tombs of eighth century, Mater Thesis in Archeology, TarbiatModarres University.
- Asgari S (1998) Vernacular architecture of Mazandaran, three tombs of Sari (In Persian). Javidan Heritage.
- Zemorshedi H(1994) Reviewing in Architecture and Vaulted Works of Iran, KeihanFarhangi.
- Memarian Q (1988) Vaulted Sructures in Islamic Architecture of Iran. Elm o Sanat University Press, Tehran.
- Wilber D, Golombek L (1995) The Timurid architecture of Iran and Turan.Cultural Heritage.
- Saoud R (2003) Muslim Architecture Under Seljuk Patronage, foundation for science technology and civilization.
- Bemanian M, Okhovat H, Baqaiee P (2010) The usage of geometry and proportions in architecture.
- Nosrati M (1998) Sacred Art in Tomb Towers, KeihanFarhangi 145:38-40.
- Pirnia M (2008) Iranian Architecture.
- Pirnia M (1993) Iranian Islamic Architecture, SorushDanesh Press.
- Pirnia M (2004) Stylistics of Iranian Architecture.
- Pope A (2004) Persian Architecture. Akhtaran Press.
Relevant Topics
- Architect
- Architectural Drawing
- Architectural Engineering
- Building design
- Building Information Modeling (BIM)
- Concrete
- Construction
- Construction Engineering
- Construction Estimating Software
- Engineering Drawing
- Fabric Formwork
- Interior Design
- Interior Designing
- Landscape Architecture
- Smart Buildings
- Sociology of Architecture
- Structural Analysis
- Sustainable Design
- Urban Design
- Urban Planner
Recommended Journals
Article Tools
Article Usage
- Total views: 17641
- [From(publication date):
March-2015 - Apr 20, 2025] - Breakdown by view type
- HTML page views : 12838
- PDF downloads : 4803