Research Article Open Access
Genotype × Environment Interaction and Stability Estimate for Grain Yield of Upland Rice Genotypes in Nigeria
Maji AT1, Bashir M2, Odoba A1, Gbanguba AU1 and Audu SD1*
1National Cereals Research Institute Badeggi, Niger state. Nigeria
2National Biotechnology Development Agency, Lugbe, Abuja, Nigeria
- Corresponding Author:
- Audu SD
National Cereals Research Institute Badeggi
Niger state, Nigeria
E-mail: Saudatu28@gmail.com
Received December 23, 2014; Accepted February 26, 2015; Published February 28, 2015
Citation: Maji AT, Bashir M, Odoba A, Gbanguba AU, Audu SD (2015) Genotype × Environment Interaction and Stability Estimate for Grain Yield of Upland Rice Genotypes in Nigeria. J Rice Res 3:136. doi: 10.4172/2375-4338.1000136
Copyright: © 2015 Maji AT, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited
Visit for more related articles at Rice Research: Open Access
Abstract
Genotype × environmental interaction and stability estimate were investigated on grain yield of 30 upland rice varieties at Sabon Daga, Amakama, Yandev and Uyo in 2003. The experiments were laid out in a randomised complete block design with three replications. AMMI Anova for grain yield revealed no significant different among genotypes (P<0.01), but there is significant difference on environments and the interaction. The significant different on the interaction indicates that, the genotypes respond differently across the different environments. The partitioning of GGE through GGE biplot analysis showed that principal component1 and principal component 2 accounted for 62.21% and 28.57% of GGE sum of squares respectively, explaining a total of 90.78% variation. AMMI 2 biplot revealed that, genotype ART16-9-3-15-3-B-1-1 (8) gave the highest mean yield of 2925 kg/ha with high main additive effect better than the check varieties. Hence, the genotype would be considered more adapted to wide environments than the rest of genotypes. Environments, such as Sabon Daga and Amakama could be regarded as a more stable site for high yielding rice varieties compare to the other locations.
Keywords
Genotype; Stability; ANOVA
Introduction
Rice (Oryza sativa L.) is the second most important cereals crop, grown in more than 144 million farm worldwide, most certainly than any other crop on a harvested area of about 162 million ha [1]. The author also reported that, global rice production rise more than tripled between 1961 and 2010, with a compound growth rate of 2.24% per year, most of the increase in rice production was due to higher yields, which increase at annual average rate of 1.74%, compared with an annual average growth rate of 0.49% for area harvested. He further stated that, per capital consumption of rice continues to grow fast particularly in most sub-Saharan Africa, where high population growth with changing consumer preferences is causing rapid expansion in rice consumption. In countries such as Kenya, Niger, Nigeria and Tanzania people are moving away from maize and cassava to rice as their income rises. Along with strong population growth, the rapid rise in per capita consumption also contributed to such rapid growth in rice demand.
In Nigeria, rice is a leading staple crop cultivated in virtually all the agro-ecological zones of country, from the mangrove and swamps environment of the coastal areas, to the dry zones of the Sahel in the North [2]. On the other side, the demand for rice has been soaring over years, since mid 1970’s rice consumption in Nigeria has risen tremendously growing by 10.3% per annum, as a result of accelerating population growth rate, increasing per capita consumption, rapid urbanization, increase income levels, and associated changes in family occupational structures [2-4]. GRISP [1] reported that, Nigeria is blessed with three major rice production environments and their coverage is rainfed lowland (69.0%), irrigated lowland (2.7%) and rainfed upland (28.3%). More than 90% of Nigeria’s rice is produced by resource poor small-scale farmers, while the remaining 10% is produced by cooperate/commercial farmers.
Upland rice is grown in rainfed, naturally well drained soils without surface water accumulation, normally without pyretic water supply, and normally not bunded. In the upland environment, rice cultivation is challenged by drought, low adoption of improved varieties, soil acidity and general soil infertility, poor weed control, limited capital investments, labor shortages and low mechanization, resulting in low yield range from 1.0 to 1.7 t/ha compared with a potential of 2.0-4.0 t/ha. Most upland rice is grown on small subsistence farms with few purchased inputs and most production is for family consumption. Therefore developing high yielding upland varieties combine with tolerant to biotic and abiotic stress will contribute substantially to poverty alleviation, especially, for resource constrained households and can increase household food security.
Numerous statistical methods have been developed for the analysis of Genotype by Environment Interactions (GEI) and phenotypic stability [5-8]. Regression technique has been widely used [9,10] due to its ease and the fact that its information on adaptive response is easily applicable to locations. The Principal Component Analysis (PCA) method that shows the mean squares of the principal components axes [11] has also been used. [12] Zobelet al. compared the traditional statistical analysis such as Analysis of Variance (ANOVA), Principal Component Analysis (PCA) and Linear Regression with AMMI analyses, and showed that the traditional analyses were not always effective in analyzing the multi-environment trial data structure. The ANOVA is an additive model that describes main effects effectively and determines if GE interaction is a significant source of variation, but it does not provide insight into the patterns of genotypes or environments that give rise to the interaction. The PCA is a multiplicative model that contains no sources of variation for additive G or E main effects and does not analyze the interactions effectively. The linear regression method uses environmental means, which are frequently a poor estimate of environments, such that the fitted lines in most cases account for a small fraction of the total GE and could be misleading [13-15].
Additive main effects and multiplicative interaction (AMMI) has been proved to be a suitable method for depicting adaptive responses [15-17]. AMMI analysis has been reported to have significantly improved the probability of successful selection [17] and has been used to analyse GxE interaction with greater precision in many crops [13,15,18]. The model combines the conventional analysis of variance for genotype and environment main effects with principal components analysis to decompose the GEI into several Interaction Principal Component Axes (IPCA). With the biplot facility from AMMI analysis, both genotypes and environments are plotted together on the same scatter plot and inferences about their interaction can be made.
This study, reports the use of AMMI model to analyse yield data of thirty genotypes of upland rice evaluate in four locations. The objectives is (1) to determine the nature and magnitude of G × E interaction effect on grain yield in diverse environment (2) to determine environment where upland rice genotypes would be adapted and produce economically competitive yield.
Materials and Methods
Thirty upland rice varieties selected from breeding task force upland mega environmental trial (MET) of 2012 are composed as preliminary yield trial (PET) in National Cereals Research Institute, Badeggi rice breeding unit, evaluated during 2013 cropping season at four locations as shown in Table 1. The experiment was conducted in a randomised complete block design in three replication, The plot size was 4 m × 3 m square with 20 cm inter and intra row spacing. Fertilizer application was 40 kg N, 40 Kg P2O5 and 40 Kg K2O at transplanting, while additional 40 kg N per ha was used as top dressing at vegetative and panicle initiation in equal split. Weed control was by chemical at 21 days after transplanting (DAT) using a formulation of Propanil and 2-4-D (Orizo Plus(R)), and was followed by hand weeding at 43 days after transplanting. Grain yield was recorded after harvest at 14% moisture content and was subjected to analysis of variance (ANOVA) using Crop Stat statistical package. In order to determine the effect of genotype × environment interaction on rice grain yield, the data was further subjected to an additive main effect and multiplicative interaction (AMMI), GGE-biplot and Boxplot analysis using Breeding View (BV) statistical package.
| Location | Longitude | Latitude | State | Agro-Ecological Zones |
|---|---|---|---|---|
| SabonDaga | 090.73’N | 060.52’ E | Niger | Southern Guinea Savannah |
| Amakama | 050.29’ N | 070. 33’ E | Abia | Rain Forest zone |
| Uyo | 040. 50’ N | 070. 56’ E | AkwaIbom | Rain Forest zone |
| Yandev | 080.47’ N | 070.22’ E | Benue | Southern Guinea Savannah |
Table 1: Geographic description of coordinates of the trial location in 2013 cropping season.
Results and Discussion
AMMI analysis of variance
The fit of an additive model to the rice grain yield data are presented in Table 2. It showed that, there is no significant difference in genotypes main effect. However, significant differences (P<0.01) exist among environments and genotypes × environment (G × E) interaction, PCA1 and PCA2 main effects. The environments are characterised by the average performance of the genotypes at a particular environment and the results indicates that, the environments differ significantly. Marcos et al. [19] reported that, environmental difference is not a major concern, but the differences that exist between the genotypes. No significant genotype main effect indicates that genotypes are not different in their mean performance across environment. Although genotypic and environmental scores are deemed to represent genetic and environmental qualities, they come from a mathematical procedure, a principal components analysis on the GEI [12,20] that maximizes the variation explained by the products of the genotypic and environmental scores. The first two PCA explains most of the variation,in grain yield. This is reflected in Table 2, which shows the results from the AMMI model to the grain yield data. In the AMMI model, GEI is explained by two axes (principal component 1, PCA1, and principal component 2, PCA2) that are highly significant respectively, both with an associated (P<0.001). Thus the interaction of the 30 genotypes across four environments was best predictable by the first two principal components.
| Source | d.f. | s.s. | m.s. | v.r. | F pr |
|---|---|---|---|---|---|
| Genotypes | 29 | 3120724 | 107611 | 1.20 | 0.2529 |
| Environments | 3 | 79273389 | 26424463 | 295.33 | <0.001 |
| Interactions | 87 | 7784210 | 89474 | 3.37 | <0.001 |
| IPCA 1 | 31 | 4842595 | 156213 | 5.88 | <0.001 |
| IPCA 2 | 29 | 2224187 | 76696 | 2.89 | 0.0035 |
| Residuals | 27 | 717428 | 26571 |
Table 2: AMMI analysis of variance for grain yield of 30 rice genotype across 4 environments.
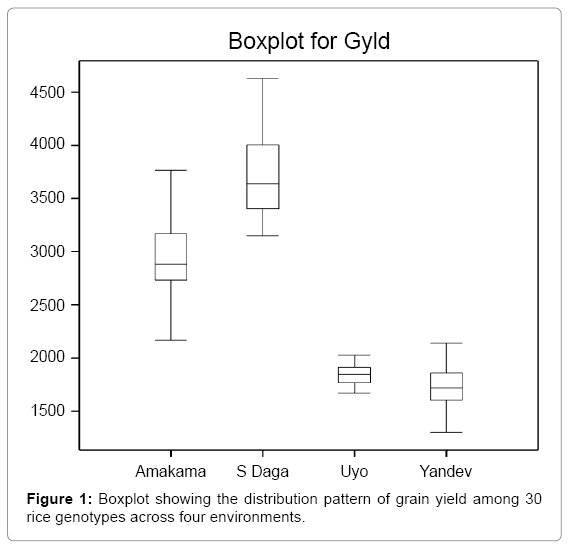
Box Plot is a convenient way of graphically depicting group of numerical data through their qualities. It displays varieties in samples of a statistical population without making any assumptions of the underlying statistical distribution [21]. The spacing between the different parts of the box indicates the degree of dispersion (spread) of the data and allows visually estimate of inter-quartile mean, median and mode. Result in Figure 1 is showing the distribution pattern of grain yield of 30 rice genotypes across four environments. The result revealed that, Sabon daga has the highest mean grain yield of 3692 kg/ha (Table 3) with large variance followed by Amakama with mean yield of 2940 kg/ha, while Yandev and Uyo discriminate less between genotypes with mean of 1719 and 1846 kg/ha, respectively. This is reflected in the smaller variance Przystalski [22] reported that, the genetic variance tends to be larger in better environments than in poorer environments.
| Location | Range | Lower quartile | Upper quartile | Std. d | Mean | %cv | s. sq |
|---|---|---|---|---|---|---|---|
| S Daga | 1477 | 3405 | 4004 | 398.4 | 3692 | 10.79 | 4603301 |
| Amakama | 1600 | 2733 | 3167 | 406.3 | 2940 | 13.82 | 4787551 |
| Uyo | 358 | 1768 | 1911 | 98.7 | 1846 | 5.35 | 282616 |
| Yandev | 839 | 1606 | 1861 | 206.1 | 1719 | 11.99 | 1231466 |
Table 3: Showing the statistical distribution of environmental performance
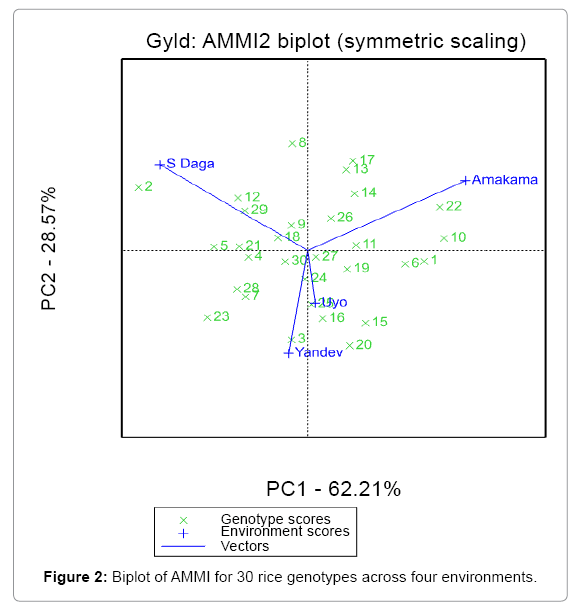
A desirable property of the AMMI model is that, the genotypic and environmental scores can be used to construct powerful graphical representations called biplots [19] that help to interpret the GEI, the biplot showing both genotypes and environments in the same plot. The author further stated that, biplots facilitate the exploration of relationships between genotypes and/or environments. Genotypes that are more similar to each other are closer to each other in the plot than genotypes that are less similar. The same is true for environments. Genotypes/environments that are alike tend to cluster together. Result in Figure 2 indicates that, S Daga location has the highest mean yield 3692 kg/ha, while ART12-1L6P7-8-1-B-1 (2) is the genotype with the highest mean yield. The result also shows that, there is no correlation between Amakama and Yandev/ Uyo locations. The projection of ART12-1L6P7-8-1-B-1 (2) and ART16-9-3-15-3-B-1-1 (8) on to S Daga axis reflects the higher mean yield performance of the genotypes. Similarly in Amakama genotype ART3-9L9P3-1-B-2 (22) and ART2- 6L6P6-1-B-1(10) performed best in the location, while genotype ART12-1L6P7-8-1-B-1 (2) and ART16-9-3-15-3-B-1-1 (8) has positive interaction with S Daga. It is also predicted that, genotype ART3- 3L12P9-1-1-B (15), ART3-7L9P8-3-B-B-2(20) and ART3-6L3P9- B-B-2 (16) has negative GEI values in S Daga because their projections were towards the negative direction of S Daga arrow. Also genotype FARO55 (23), ART16-22-1-1-2-B-1-1 (7) and WAB706-27-K5-KB-2 (28) have negative interaction with Amakama location. Generally, there was a poor yield performance in Yandev and Uyo locations as shown in Figure 2.
AMMI 2 biplot display
In the AMMI 2 biplot, (Figure 2) the environmental scores (locations) are joined to the origin by side lines. Sites with short vectors do not exert strong interactive forces (Uyo and Yandev). While those that long vectors exert strong interaction (S. Daga and Amakama). Weikai Yan reported that, a short vector indicates a location in which there is a small range of genotype performance.
The vertical Y axis is showing the best one dimension measure of the GE effect for each genotype. Thus, genotypes close to the X axis have a small GE effect, while those far away the X axis in either the positive or negative directions has a large GE effect. Figure 2 shows that, genotype ART10-1L12P2-1-B-1(1) and ART16-16-5-23-1-B-1-1 (6) has a small GE effect, which is considered stable and less influenced by the environments.
Weikai Yan reported that, If the angle between two genotype vectors is less than 90 degrees, then the genotypes are positively correlated, tending to do well, or badly, in the same environment. But if the angle between the vectors of two genotypes is greater than 90 degrees, then they tend to perform differently over the trial environments. If the angle between two genotype vectors is 90 degrees, their performance is independent, of each other. Figure 2 shows that, ART16-9-3-15- 3-B-1-1 (8), ART3-9L9P3-1-B-2 (22) and ART3-6L3P9-B-B-3 (17) are positively correlated. However, there is negative correlation between ART16-9-3-15-3-B-1-1 (8), ART10-1L12P2-1-B-1 (1) and ART16-16- 5-23-1-B-1-1(6). Also, there is no correlation between ART16-9-3-15- 3-B-1-1 (8) and ART3-12L11P2-B-B-1 (11) ART16-12-22-4-1-B-1-1 (5), ART3-8L6P6-5-B-2(21) and FARO58 (24). The ideal genotype is the genotype with high performance combined with good stability.
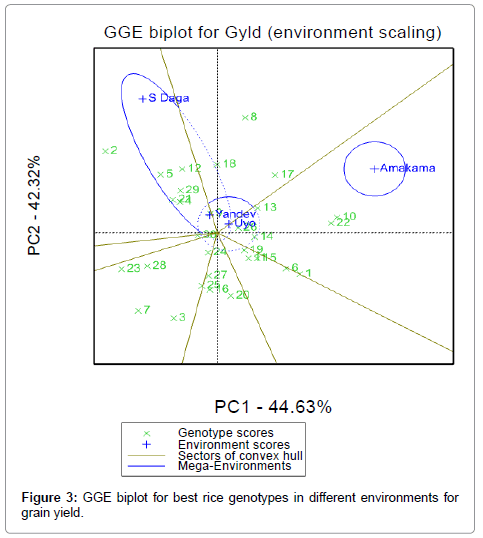
GGE biplot also allows the partitioning of environment into groups. In this study, three environmental groups are identified as shown in the Figure 3. S Daga and Amakama in the upper part are two different environments, while Yandev and Uyo close to each other at the origin form one similar environment. The partitioning of GGE through GGE biplot analysis of grain yield showed that, PC1 and PC2 accounted for 44.63% and 42.32% of GGE sum of squares respectively, explaining a total of 86.95% variation. GGE biplot shows the cosine of the angle between two environment vectors is proportional to the correlation between those two environments that is an angle of less than 90 degrees. The environments are positively correlated [21]. The result in Figure 3 shows a negative correlation between S Daga and Amakama indicating that different genotypes performed differently across the two environments. The distance between S Daga and Amakama in the GGE biplot is related to the independence of the genotype performance in the two environments, while the closeness of Yandev and Uyo location signifies that genotypes response patterns are similar in yield performance. Therefore to save resources, it is better to select only one location out of this group for further trials, Yandev location could be selected in group 3 as it has the longest vector (Tables 4 and 5).
| S/no. | Genotype | Location Mean Grain Yield (Kg/ha) | MeanGrain yield (Kg/ha) | |||
|---|---|---|---|---|---|---|
| SabonDaga | Amakama | Uyo | Yandev | |||
| 1 | ART10-1L12P2-1-B-1 | 3150 | 3333 | 1870 | 1611 | 2491 |
| 2 | ART12-1L6P7-8-1-B-1 | 4627 | 2500 | 1743 | 1739 | 2652 |
| 3 | ART15-4-14-63-2-B-1 | 3214 | 2367 | 1810 | 1678 | 2267 |
| 4 | ART16-12-17-3-4-B-1-1 | 4004 | 2800 | 1849 | 1936 | 2647 |
| 5 | ART16-12-22-4-1-B-1-1 | 4248 | 2767 | 1861 | 2028 | 2726 |
| 6 | ART16-16-5-23-1-B-1-1 | 3225 | 3267 | 1810 | 1681 | 2496 |
| 7 | ART16-22-1-1-2-B-1-1 | 3417 | 2167 | 1794 | 1369 | 2187 |
| 8 | ART16-9-3-15-3-B-1-1 | 4429 | 3500 | 2016 | 1756 | 2925 |
| 9 | ART16-9-4-17-3-B-1 | 3856 | 2967 | 1771 | 1708 | 2576 |
| 10 | ART2-6L6P6-1-B-1 | 3405 | 3767 | 1854 | 1939 | 2741 |
| 11 | ART3-12L11P2-B-B-1 | 3428 | 3067 | 1712 | 1611 | 2455 |
| 12 | ART3-12L2P1-B-B-1 | 4255 | 2933 | 1804 | 1778 | 2693 |
| 13 | ART3-1L6P5-1-B-1 | 3783 | 3300 | 1714 | 1450 | 2562 |
| 14 | ART3-2L4P5-1-B-1 | 3599 | 3167 | 1910 | 1300 | 2494 |
| 15 | ART3-3L12P9-1-1-B | 3334 | 3100 | 1918 | 2083 | 2609 |
| 16 | ART3-6L3P9-B-B-2 | 3291 | 2700 | 1767 | 1817 | 2394 |
| 17 | ART3-6L3P9-B-B-3 | 3954 | 3500 | 2028 | 1494 | 2744 |
| 18 | ART3-7L3P3-B-B-2 | 4132 | 3167 | 1843 | 2139 | 2820 |
| 19 | ART3-7L9P8-1-B-B-2 | 3468 | 3067 | 1671 | 1861 | 2517 |
| 20 | ART3-7L9P8-3-B-B-2 | 3166 | 2800 | 1931 | 1917 | 2454 |
| 21 | ART3-8L6P6-5-B-2 | 4048 | 2767 | 1790 | 1894 | 2625 |
| 22 | ART3-9L9P3-1-B-2 | 3423 | 3700 | 1992 | 1583 | 2675 |
| 23 | FARO55(NERICA1) | 3712 | 2200 | 1740 | 1833 | 2371 |
| 24 | FARO58(NERICA7) | 3576 | 2800 | 1986 | 1689 | 2513 |
| 25 | FARO59(NERICA8) | 3354 | 2667 | 1722 | 1756 | 2375 |
| 26 | NERICA11 | 3680 | 3100 | 1768 | 1597 | 2536 |
| 27 | NERICA18 | 3446 | 2733 | 1911 | 1394 | 2371 |
| 28 | WAB706-27-K5-KB-2 | 3679 | 2367 | 1903 | 1606 | 2389 |
| 29 | WAB788-16-1-1-2-HB | 4121 | 2833 | 1993 | 1606 | 2638 |
| 30 | WAB891-SG12 | 3732 | 2800 | 1887 | 1728 | 2537 |
| LSD @ 0.05% | NS | NS | NS | NS | NS | |
| % CV | 19.7 | 24.3 | 7.4 | 10.2 | 14.3 | |
Table 4: Mean grain yield of upland rice varieties across four location in Nigeria.
| s/no. | Trt/no. | Genotype | Sensitivity | Mean | Mean square deviation |
|---|---|---|---|---|---|
| 1 | 3 | ART15-4-14-63-2-B-1 | 0.6666 | 2453 | 7633 |
| 2 | 13 | ART3-1L6P5-1-B-1 | 0.7323 | 2267 | 22924 |
| 3 | 18 | ART3-7L3P3-B-B-2 | 0.7335 | 2609 | 49011 |
| 4 | 28 | WAB706-27-K5-KB-2 | 0.7814 | 2394 | 5782 |
| 5 | 22 | ART3-9L9P3-1-B-2 | 0.8351 | 2374 | 5527 |
| 6 | 5 | ART16-12-22-4-1-B-1-1 | 0.8481 | 2491 | 201906 |
| 7 | 7 | ART16-22-1-1-2-B-1-1 | 0.8652 | 2496 | 141668 |
| 8 | 9 | ART16-9-4-17-3-B-1 | 0.8931 | 2187 | 114581 |
| 9 | 29 | WAB788-16-1-1-2-HB | 0.8947 | 2371 | 199216 |
| 10 | 16 | ART3-6L3P9-B-B-2 | 0.9020 | 2513 | 10073 |
| 11 | 10 | ART2-6L6P6-1-B-1 | 0.9223 | 2517 | 52360 |
| 12 | 30 | WAB891-SG12 | 0.9226 | 2741 | 337543 |
| 13 | 23 | FARO55(NERICA1) | 0.9326 | 2388 | 107737 |
| 14 | 4 | ART16-12-17-3-4-B-1-1 | 0.9480 | 2371 | 38952 |
| 15 | 15 | ART3-3L12P9-1-1-B | 0.9724 | 2454 | 43037 |
| 16 | 25 | FARO59(NERICA8) | 0.9836 | 2537 | 8713 |
| 17 | 11 | ART3-12L11P2-B-B-1 | 0.9957 | 2675 | 324508 |
| 18 | 1 | ART10-1L12P2-1-B-1 | 1.0467 | 2647 | 55744 |
| 19 | 14 | ART3-2L4P5-1-B-1 | 1.0767 | 2536 | 17852 |
| 20 | 26 | NERICA11 | 1.0896 | 2625 | 68563 |
Table 5: Twenty environmentally sensitive rice varieties in grain yield across four upland rice growing environments in 2013 using AMMI analysis.
Conclusion
AMMI statistical model is a tool in selecting the most suitable and stable high yielding crop genotype for specific as well as for diverse environments. In the present study, AMMI model has shown that the largest proportion of the total variation in rice grain yield in the genotypes is attributed to environments. Most of the genotypes showed environment specificity. The mean grain yield value of genotypes averaged over environments indicated that ART16-9-3-15-3-B-1-1 (8) had the highest mean grain yield 2925 kg/ha. Genotypes ART10- 1L12P2-1-B-1(1) and ART16-16-5-23-1-B-1-1 (6) has a small GE effect, which is considered as stable and less influenced by the environment.
References
- GRISP (Global Rice Science Partnership) (2013). Rice almanac, 4th edition. Los Banos (Philippines) International Rice Research Institute: 283
- AkandeSO(2002)An Overview of the Nigerian Rice Economy, NISER, Ibadan
- AkpokodjeGF, LançonO, Erenstein (2001)Nigeria's Rice Economy: State of the Art. Project Report - The Nigerian Rice Economy in A Competitive World: Constraints, Opportunities And Strategic Choices. Bouake: WARDA:11-55.
- UNEP (United Nations Environment Programme) (2005). Annual report; Division of Early Warning and Assessment (DEWA) Nairobi, 00100, Kenya
- Hill,J (1975) Genotype- environment interaction- A challenge for plant breeding. J. Agri Science, Cam 85: 477-493
- Lin CS, MR Binn, LP Lefkovitch (1986) Stability an alysis: Where do we stand. Crop Sci 26: 894-900.
- Crossa J, Gauch HGJ, Zobel RW (1990) Additive main effects and multiplicative interaction analysis of two international maize cultivar trials. Crop Science 30: 493-500
- Flores GV, Daga A, Kalhor HR, Banerjee U (1998) Lozenge is expressed in pluripotent precursor cells and patterns multiple cell types in the Drosophila eye through the control of cell-specific transcription factors.Development 125: 3681-3687.
- Eberhart SA, Russell WA (1966) Stability parameters for comparing varieties. Crop Sci 6: 36-40.
- Perkins JM, Jinks JL (1968) Environmental and genotype-environmental components of variability. 3. Multiple lines and crosses.Heredity (Edinb) 23: 339-356.
- Gauch HG, Furnas RE (1991) Statistical analysis of yield trials with MATMODEL. Agronomy Journal 83:916-920.
- Gauch HG(1988) Model selection and validation for yield trials with interaction. Biometrics 44: 705-15
- Crossa J, Fox PN, Pfeiffer WH, Rajaram S, Gauch HG Jr (1991) AMMI adjustment for statistical analysis of an international wheat yield trial. TheorAppl Genet 81: 27-37
- Zobel RW, Wright MJ, Gauch HG (1988) Statistical analysis of a yield trial. Agronomy Journal 80: 388-393.
- Kayode A Sanni OJ, Ariyo DK, Ojo G, Gregorio, etal.(2009) Additive Main Effects and Multiplicative Interactions Analysis of Grain Yield Performances in Rice Genotypes Across Environments. Asian Journal of Plant Sciences8: 48-53.
- Gauch HG (1993) Matmodel version 2.0. AMMI and related analysis for two way data matrics. Micro computer power, Ithaca, New York, USA
- Gauch HG Jr, Zobel RW (1989) Accuracy and selection success in yield trial analyses.TheorAppl Genet 77: 473-481.
- Gauch HG (1990) Using Interaction to Improve Yield Estimates. In: Kang MS (ed.) Genotype-by-Environment Interaction and Plant Breeding, Department of Agronomy, Louisiana State University, Baton Rouge, Louisiana,141-150.
- Marcos M, Jean-Marcel R, Fred A (2013) The statistical analysis of multi-environment data: modelling genotype-by-environment interaction and its genetic basis; Wageningen University, Netherland
- Gabriel K (1978) Least squares approximation of matrices by additive and multiplicative models. J. R. Stat. Soc. B 40: 186-196
- McDermott B, Coe R (2012). An Easy Introduction to Biplots for Multi-Environment Trials; Statistical Services Centre, University of Reading, UK and World Agroforestry Centre, Kenya
- Przystalski M, Osman A, Thiemt EM, Rolland B,et al.(2008). Comparing the performance of cereal varieties in organic and non-organic cropping syste ms in different European countries. Euphytica 163:417-433
Relevant Topics
- Basmati Rice
- Drought Tolerence
- Golden Rice
- Leaf Diseases
- Long Grain Rice
- Par Boiled Rice
- Raw Rice
- Rice
- Rice and Aquaculture
- Rice and Nutrition
- Rice Blast
- Rice Bran
- Rice Diseases
- Rice Economics
- Rice Genome
- Rice husk
- Rice production
- Rice research
- Rice Yield
- Sticky Rice
- Stress Resistant Rice
- Unpolished Rice
- White Rice
Recommended Journals
Article Tools
Article Usage
- Total views: 15306
- [From(publication date):
April-2015 - Apr 05, 2025] - Breakdown by view type
- HTML page views : 10645
- PDF downloads : 4661