Research Article Open Access
Fusion of Multi-slice MR-Scan Images with Genetic Algorithm with Curvelet-transform
Dhanesh Kumar Solanki1*, Naresh Solanki2 and Mohammed Fakhreldin Adam2
1Department of Computer Science Engineering, Birla Institute of Technology PILANI, Kota Medical College, Rajasthan, India
2Assistant professor, University Malaysia Pahang, Malaysia
- *Corresponding Author:
- Dhanesh Kumar Solanki
Department of Computer Science Engineering
Birla Institute of Technology PILANI
Kota Medical College, Rajasthan, India
Tel: +91-9414062512
E-mail: solankidhanesh@gmail.com
Received date: September 03, 2014; Accepted date: October 24, 2014; Published date: October 31, 2014
Citation: Solanki DK, Solanki N, Adam MF (2014) Fusion of Multi-slice MR-Scan Images with Genetic Algorithm with Curvelet-transform. Lovotics 2:109. doi:10.4172/2090-9888.1000109
Copyright: © 2014 Solanki DK, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permitsunrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Lovotics
Abstract
On considerable progress on Medical Image fusion techniques, many algorithm are used from intensity-huesaturation (IHS), principal component analysis (PCA), multi resolution analysis based method & Artificial Neural Network (ANN), but all these algorithm had heavily degrade the brightness of the input images. In IHS fusion, it converts a low resolution color images from RGB space into the IHS color space and a combined IHS with PCA to improve fused image quality but it generates several drawback, (a) The Pixel-level fusion- method are sensitive to accuracy (gives low accuracy), (b) The color channel of input spectrum should be less than or equal to IHS transform (created very large spectrum) and in ANN-based fusion include: (1) The long iteration time of the ANN and the need to manually parameterize it before each fusion; (2) An occasional failure to converge, such as in the PCNN-based method when some neurons did not fire during the whole iteration.
Keywords
Multi-Resolution Image(MR Images) Fusion; Genetic Algorithm; Curvelet transformation; Copulas
Background
Medical image fusion can be performed at three broad levels: pixel level, feature level, and decision level. Pixel based fusion is performed on a pixel-by-pixel basis, generating a fused image in which information associated with each pixel is selected from a set of pixels in the source images. Medical image fusion at the feature level requires the extraction of salient environment-dependent features, such as pixel intensities, edges, or textures [1-3]. Decision-level fusion involves merging information at a higher level of abstraction, combining the results from multiple algorithms to yield a final fused decision. At this level, input images are processed individually for information extraction. The obtained information is then combined by applying decision rules to reinforce a common interpretation [4].
For multi-resolution analysis (MRA)-based fusions, such as the pyramid transformation, have been used for nearly three decades. Pyramid-based image fusion methods, which were all developed from the Gaussian pyramid transform, have been extensively modified and widely used. Wavelets and their related transform represent another widely used technique in this category. Wavelet transforms provide a framework in which an image is decomposed into a series of coarseresolution sub-bands and multi-level finer-resolution sub-bands. The contrast pyramid fusion method loses too much source information to obtain a clear, subjective image; the ratio pyramid method produces lots of inaccurate information in the fused version, and the morphological pyramid method creates a large number of artifacts that do not exist in the original source images. Wavelets and their related transform represent another widely used technique in this category. Wavelet transforms provide a framework in which an image is decomposed into a series of coarse-resolution sub-bands and multi-level finer-resolution sub-bands [5].
Many times multi-slice transform based image fusion methods assume that the underlying information is the salient features of the original images, which are linked with the decomposed coefficients, This assumption is reasonable for the transform coefficients that correspond to the transform bases which are designed to represent the important features, such as edges and lines of an image. Wavelets and related multi-slice transforms are working with a limited dictionary; each multi-slice transform has its own advantages and disadvantages [6].
Motivation
Progress on medical image fusion techniques has been made, and various fusion algorithms have been developed. Medical image fusion can be performed at three broad levels: pixel level, feature level, and decision level. Pixel based fusion is performed on a pixel-by-pixel basis, generating a fused image in which information associated with each pixel is selected from a set of pixels in the source images. Medical image fusion at the feature level requires the extraction of salient environment- dependent features, such as pixel intensities, edges, or textures. Decision-level fusion involves merging information at a higher level of abstraction, combining the results from multiple algorithms to yield a final fused decision and also with this medical Images are exchanged for number of reasons, for example tele-conference among clinicians interdisciplinary exchanged between radiologists for consultative purpose and distant learning of medical personal. Like, the spatial precision of fMRI could be complemented with the temporal precision of EEG to provide unprecedented spatiotemporal accuracy [7].
A chief purpose of multimodal fusion is to access the joint information provided by multiple imaging techniques, which in turn can be more useful for identifying dysfunctional regions implicated in many brain disorders. This is a complicated endeavour, and can generate results that are not obtainable using traditional approaches which focus upon a single data type or processing multiple datasets individually [1].
In order to overcome the computational complexity and manual parameterization in MRA-based fusion, as well as the long iteration time of ANN-based fusion. So, we decompose an image into multi-layers of the same size as the original. Similar to the wavelet-like method, we decompose an image into coarse and detailed layers and for jointly analyzing multimodal data are to take maximal advantage of the crossinformation of the existing data, and thus may discover the potentially important variations which are only partially detected by each modality. Approaches for combining of fusion data in brain imaging can be more conceptualized as having a place on an analytic spectrum with mata-analysis to examine convergent evidence at one end and largescale computational modelling.
Challenges often come from the fact that conclusions need to be drawn from high dimensional and noisy brain imaging data from only a limited number of subjects. Hence efficient and appropriate methods should be developed and chosen carefully.
Research Methodology
Meta-heuristic Genetic Algorithm (GA) approach with curvelet transforms
For the higher accuracy and best pixel based fusion of Multi-slice image I am using Meta-heuristic Genetic Algorithm Approach with curve-let transform. Thus for more effectiveness of image fusion techniques, one divergence measures are derived from algorithm [8]:
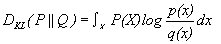 (1)
(1)
With the help of divergence measures equation. (1) can be re written as
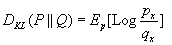 (2)
(2)
Where
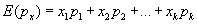 (3)
(3)
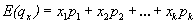 (4)
(4)
& probability p & q are:-
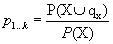 (5)
(5)
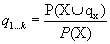 (6)
(6)
Where p(x) and q (x) are probability density function of X and Y respectively and divergence based information can be considered as the special case of the divergence between the joint probability density function and the product of the marginal probability density functions.
The divergence with Gaussian state that the outward probability of a vector field through a closed surface is equal to the volume integral divergence over the region inside the surface, Hence it states that the sum of all sources minus the sum of all sinks gives the net flow out of a region. So, similarly the values of E(Px), E(Qx) and the probability of p and q, will give a flow of data which is must necessary for the fusion of MR Images with GA. the values of equation will very helpful for directional characteristics with Curvelet transform, this above equation (1) will be able to provide the direction multi-slice fusion and its solution under GA to minimize the FS values.
Curvelet transform has direction characteristics, and its base supporting session satisfies content anisotropy relations, except have multi-scale wavelet transform and local characteristics. Here from equation. 1 to equation. 6 will provide the initial probability for image fusion. While performing the Meta heuristic with G, We get these three Issues and to solve these three issues, I had used four approaches which are used to provide the probability to solve the image fusion and help us to get rid these issues in image fusion and these above stated below.
Issues
Neighbor filtrations: While performing the Genetic Neural Network, we need to find the best solution for each images fusion because each image can’t fuse on any other images because if we fuse two non comparable image over each other than the output will be something else and more disturbing to get real data, for this we need to check the Neighbor Images which can fuse on other images and get the best solution from the fusion. So this creates a very big issue while performing the fusion which is known as Neighbor Filtration and to solve this issue I purposed two approaches and these are Linear Superposition Image Fusion &Non-Linear method MR Image Fusion under these approaches we need to find the best paring images as Neighbor which can fused and help us to get the solution out of it and under this each step will check the mutual information of images for each neighbor images.
Probability for curvelet transform: In the Curvelet transformation after neighbor filtration we need to check the probability of mutual information generated by each neighbor images for perfect fusion, under this need to transform few images after the mutual information totally depend on mutual information. Under this Curvelet we need to check the maximum probability of match of two images under best Fusion symmetry (FS) and fusion factor, because these fusion factors (FF) will help us to provide the factor of transformation of images. So this FF wills responsible to any angle or mutual transformation of images, hence this create the issue of Probability of Curvelet Transformation and for its solution we can optimize probability of fusion by the approach “Optimization Approaches of Images”. Hence need to optimise the probability each time to solve this issue for make perfect Curvelet transformation.
Fusion solution for GA: For the GA neural network we need to find the best solution amongst all the images used for fusion to get best FF and FS, for this best fusion we need to break the images into the pixel fusion and every time this pixel solution will provide the best solution and help us to get mutual information required after Curvelet transformation and neigbhors filtration and just after these two issue the pixel mutual arrive to get the best solution, hence Fusion Solution became the main issue for this kind of fusion so, we need to solve this issue, and Genetic Neural Network for Pixel fusion can solve this kind of problem by pixel mutual information related to fusion process of MR Scan images.
Now as per the issues highlighted above with Meta-heuristic GA with curve-let transform, I intended for few approaches according to solve them. These approaches are stated below as per their requirement and these are used to solve the their respective issues, every issue is generated while their fusion of images and their probabilities with respect to GA and with the help of divergence measures equation. (1) & Meta-heuristic Genetic Algorithm Approach with curve-let transform, there are many approaches to pixel level fusion of spatially input images. A few generic approaches categorization according the issues and solve them of Meta-heuristic Genetic Algorithm Approach with curve-let transform for Image Fusion and these are according to serial of issue generated.
Approach to Solve the above Issues
Linear Superposition Image Fusion
Non-Linear method MR Image Fusion
Optimization Approaches of Images
Genetic Neural Network for Pixel fusion
Linear superposition image fusion: This approach is used to solve the first issue generated while performing the fusion & that was Neighbor Filtrations (Issue 1) but this issue needs two approaches to solve this issue, and the first approaches is stated below and its research method also and this is first step to solve issue and fuse the image after getting Neighbor information and after this step we need to check with Non-linear Method MR Image Fusion.
For the higher accuracy in MR Image fusion, we should know the nearest neighbour for superposition of images, because every neighbor of images creates an issue to be got solved, because without knowing the accurate neighbor, we can’t superposed the images. So, with the help of Meta-heuristic Genetic Algorithm Approach with curve-let transform divergence measures equation. (1), we can use equation. (1) modified version with probability for Linear Superposition image Fusion for the marginal densities of the image with variable x and y respectively [9].
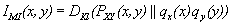 (7)
(7)
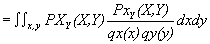 (8)
(8)
Where pXY (x,y) is the joint probability density function of the variable x and y, q X(x) and qY(y) are the marginal densities of variable x and y respectively. Mutual information can also be defined in terms of entropy measures as [10]:
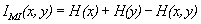 (9)
(9)
Where,
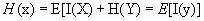 (10)
(10)
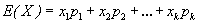 (11)
(11)
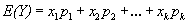 (12)
(12)
where H(x), H(y) and H(x,y) are the Shannon entropies of X and Y and the joint entropy between x & y respectively and p is relative probability of X and Y, E is expected value operator with x and y. If X and Y obey Gaussian distribution, then mutual information become one: Considering X & Y as two input image, and F as the fused image, then the mutual information based performance measure is defined as [11]:
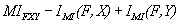 (13)
(13)
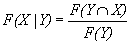 (14)
(14)
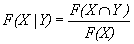 (15)
(15)
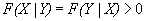 (16)
(16)
Where MI is Mutual information and FXY is a modified measure of mutual information for Neural Network & from equation. (5), equation. (6) & equation. (7) is providing the mutual probability of “F” density function and it should be greater than 0, because it will provide the multiplication (mutual) information of the X and Y.
Non-Linear method MR Image Fusion: From the probability of near neighbor MR Images, Now we can check the probability for Non- Linear Image Fusion because the Non Linear Image fusion creates lots of problem in data fusion and accurate answers, so, we need to check the possibility of higher probability, I introduce equation. (9) & equation. (13), respectively [12].
equation (9) & (13) are:-
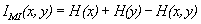 (17)
(17)
Where
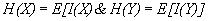 (18)
(18)
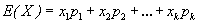 (19)
(19)
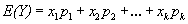 (20)
(20)
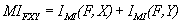 (21)
(21)
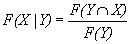 (22)
(22)
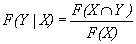 (23)
(23)
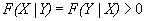 (24)
(24)
where H(x), H(y) and H(x,y) are the Shannon entropies of X and Y and the joint entropy between x & y respectively and p is relative probability of X and Y, E is expected value operator with x and y. If X and Y obey Gaussian distribution, then mutual information becomes one.
So the key to calculation of the divergence based information’s the estimation of the joint probability density for nearest neighbor Image Fusion. Approaches to this estimation problem can be classified into two categories: Non-parametric and Parametric Methods. The typical Non-parametric methods applied to image fusion processing are often referred to as the joint histogram method. The method usually requires a large amount of data of reliable results, but the operations on small size of pixel neighbors are often required. The pixel intensity distributions usually offer more stable information than pixel intensities themselves, while the joint histogram method counts the number of occurrences of pixel intensity pairs [13].
The distributions of the image pixel, the probably most straightforward way to build a fused image of several input frames is performing the fusion as a weighted superposition of all input frames. The optimal weighting coefficients, with respect to information content and redundancy removal, can be determined by a principal component analysis (PCA) of all input intensities. By performing a PCA of the covariance matrix of input intensities, the weightings for each input frame are obtained from the eigenvector corresponding to the largest eigenvalue. A similar procedure is the linear combination of all inputs in a prechosen color space (eg. R-G-B or I-H-S), leading to a false color representation of the fused image intensities in the real world usually do not obey the Gaussian or other certain probability distributions. Another simple approach to image fusion is to build the fused image by the application of a simple nonlinear operator such as max or min [7]. Here from Eq.7-Eq.24 will provide the neighbor probability in the form of image superposition linear or non-linear & then prepare image for next stage.
Optimization approaches of images: This is an approach to solve the issue Probability for Curvelet Transform (Issue 2), under this issue we need to solve all the transform probability with Curvelet Transformations of images need to fused. This will give a solution which is more optimal to transform in terms of GA approaches to fuse images and this is second step to solve issue and fuse the image after getting optimal Solution.
Since the Curvelet transform is the transformation of image in 2D or 3D for this near neigbhors and it helps us in the finding real probability of Image fusion because sometimes the image near to be rotated or transformed for its data fusion or fused Symmetry (FS). This image properties causing the many issues in fusion so, by the help of Curvelet and copula distribution function, I am solving this issue also.
If in all input images the bright objects are of interest, a good choice is to compute the fused image by a pixel-by-pixel application of the maximum operator. An extension to this approach follows by the introduction of morphological operators such as opening or closing. One application is the use of conditional morphological operators by the definition of highly reliable 'core' features present in both images and a set of 'potential' features present only in one source, where the actual fusion process is performed by the application of conditional erosion and dilation operators. A further extension to this approach is image algebra, which is a high-level algebraic extension of image morphology [14].
The basic types defined in image algebra are value sets, coordinate sets which allow the integration of different resolutions and tessellations, images and templates. For each basic type binary and unary operations are defined which reach from the basic set operations to more complex ones for the operations on images and templates. Image algebra has been used in a generic way to combine multisensory images Furthermore; the multivariate distributions require that the types of marginal distribution are consistent. If the marginal’s do not have the same type of distributions, for example, one image is Gaussian distributed, and another one is Gamma distributed, then there is no obviously known multivariate distribution model available that can estimate the associated joint probability density functions. Copulas [15] represent a mathematical relationship between the point distribution and the marginal distributions of random variables. A two-dimensional copula is a bi-variant cumulative distribution function with uniform marginal distributions on the interval (0,1).
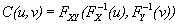 (25)
(25)
Where C(u,v) is called copula distribution function, and u=FX(x), v=FY(y) are the marginal cumulative probability distributions for variables X & Y respectively. The copula density is derived from equation (4), (5) & (6) is
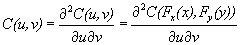 (26)[3]
(26)[3]
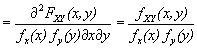 (27)[16]
(27)[16]
With the help of equation. (8), we know this equation (15), (16) & (17) already for finding the probability associate with X and Y.
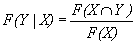 (28)
(28)
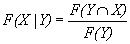 (29)
(29)
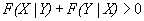 (30)
(30)
equation. (9), (10) & (11) is providing the mutual probability of “F” density function and it should be greater than 0, because it will provide the multiplication (mutual) information of the X and Y.
Where C(u,v) is the copula density function, fXY(x,y) is the joint probability density function of X & Y & fX(x), fY(y) are the marginal probability density function respectively.
The mutual information is computed by using both Gaussian assumption based method and copula method, while been computed using a Gaussian & Copula, the Copula parameter estimated by using Genetic Algorithm. Here we implement Eq.25-30 after all other above equation, the image is now ready to implement for GA.
Genetic neural network for pixel fusion: (With Gaussian components): This is also an approach to solve the Fusion Solution for GA (Issue 3) [17-20], under this approaches I solve the GA to get the best solution to find the Fusion symmetry, and this approaches will provide the best solution under pixel fusion of images and help GA and neural network to identify the best solution in terms of Curvelet transform. With this last approaches we can fuse the image and get the best solution out of it and this is last step of image fusion.
The genetic algorithm, by contrast, does not try every possible combination. It attempts instead to intelligently get closer and closer to the best solution. Therefore, far more variables can be utilized, and you can allow all values of a variable. Optimization can still take a good deal of time if you give a GA a fair number of variables, but it will be doing much more work in that amount of time. So for time and best solution, I implement Fusion Symmetry by Curvelet transform with higher probability for nearest neighbor in pixel fusion, because fusion in pixel with probability creates a issue for time and accurate looping for best solution with GA with Curvelet transform.
By the Genetics Algorithm with divergence wavelet, the mutual result will be in Ratio of pixel, So for Principal Components Analysis (PCA), because PCA fused image is very to visible image, so that a very high mutual information is generated between PCA with Gaussian with Genetic Algorithm. The PCA fused image is 'very distant' from infrared image, and so the mutual information between PCA fused image & the infrared is very low, however mutual information is always great or equals to 0. The PCA fused image still has very mutual information with input images and is mistakenly considered as the best algorithm. To avoid this type of error, the Fusion Symmetry (FS) [17] is introduced to solve this problem with the help of Gaussian and Meta- Heuristic Genetic Algorithm.
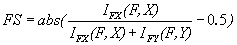 (31)
(31)
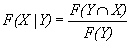 (32)
(32)
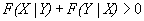 (33)
(33)
where
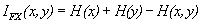 (34)
(34)
Where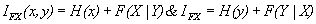 (35)
(35)
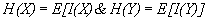 (36)
(36)
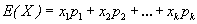 (37)
(37)
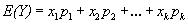 (37)
(37)
where IFX() is a modified measure of mutual information, for the divergence based information. The smaller the FS, the better performance of image fusion and also H(x), H(y) and H(x,y) are the Shannon entropies of X and Y and the joint entropy between x & y respectively and p is relative probability of X and Y, E is expected value operator with x and y. If X and Y obey Gaussian distribution, then mutual information become one All the results of image fusion performance the Gaussian copula were applied and GA method used to estimate the copula parameter. The FS measure is much better than the simple, visible image fusion respectively. This measure is called Fusion Factor (FF). The next step is to compare the methods between mutual information, divergence based information. Since fusion symmetric measure is obviously better fusion factor, hence only fusion symmetry measure is considered. According to all derived rule, the smaller FS, the better the performance of image fusion [2].
According the Mutual information between Gaussian with Copula's and divergence equation, the FS should be smaller for better performance, hence the information of all equations [6] will deal with GA to find the best solution without many repetitions probabilities, since this all entropy and their probabilities will help GA to find its best solution. The Fusion Factor (FF) will cover all probability between the mutual information with copulas and divergence. This FF is covered all FS levels to provide the best solution and help the Image in all aspect fusion's. After all above equation we processed the ready image after Equation. 30 to next level for GA to find best solution in terms of FF and FS, so this the image is processing with Eq.31-38 and after all this we got below solution [21].
Solution
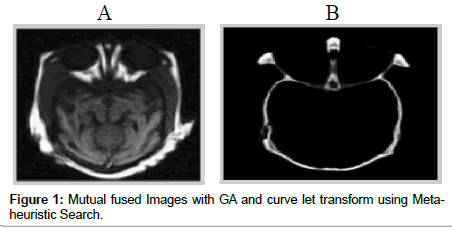
The mutual information (MI) between two image measures degree of dependence of the images (A & B). Its values are zero when Figure 1(a) and (b) are independent of each other. Mi between two source Images (A & B) and fused image F is given by histograms of images and the joint probability by the FS over FF. So, a higher MI value indicates good fusion results with lower FS values.
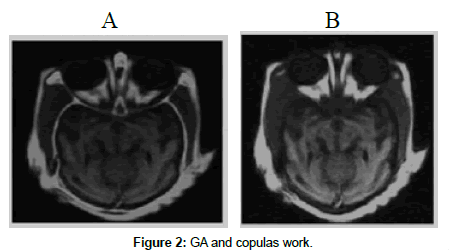
This is the divergence will check the maximum probability of mutual information if found if not then the Curvelet transform will work to transform the images for getting the probability for fusion, then the Copulas entropy is start the probability checking & fused the image initially, later on the GA and copulas will work together in below Figure 2(a) and (b) images.
After finding the maximum probability of Mutual information (MI), the Fusion Factor (FF) will work for finding the best solution in fusion method for Fusion Symmetry (FS) to be smaller because smaller the values will increase the fusion pattern and merge high intensity property reading & its variation toward next Figure 3 image.
As per the FS and FF, if a fused image is fused then it will show all properties of both images and it contain all necessary data in details, this means it contain all the data mention in both images, it will be helpful to check all required data, shown in Figure 3 “F” above. This image gives all aspect of image fusion with all details of both images in very prospectus manner and this fused image will all details according to mutual information with smaller FS. This FS fused image will show all the data according to linear pattern with reference of each images and gives a better idea about the problem in brain and other MR scanned Images.
Fusion algorithm - meta-heuristic genetic algorithm (GA) approach with curve-let transform contribution
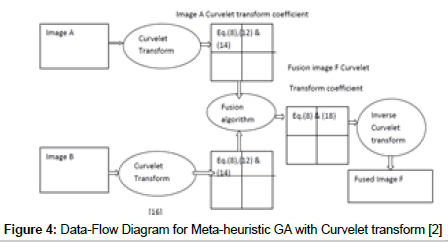
In the above, I am implementing a heuristic search with GA and Curvelet transform for the image fusion (Figure 4), to solve few issues like Neighbor filtration, Probability for curvelet transform and fusion solution for GA, In this I am using a Mutual Information for Symmetric fusion and best solution with time complexity equation. (2),(3), with equation. (5). in these equation, i am searching the mutual information for the GA to reduce the time for best solution but the curvelet transformation, i can rolate the images with transformation into RDB to IHS for the fusion and best solution in GA algorithm and optimization approaches if images. The conversion of RGB to IHS will also lead the Algorithm for the encryption for the data protection & privacy, this conversion is also helpful for data sharing across the globe and it will help us to implement other latest technology over already fused image and help us to rethink over the data and other thing from technology.
References
- Image Fusion and Its Applications, Edited by YufengZheng p. cm ISBN 978-953-307-182-4, 2011.
- Sandeep K, Yash Kumar S, Mahua B (2011) Curvelet Based Multi-Focus Medical Image Fusion Technique: Comparative Study With Wavelet Based Approach, International Conference on Image Processing, Computer Vision, and Pattern Recognition (IPCV),Worldcomp, July, Las Vagas USA.
- Henson R, Flandin G, Friston K, Mattout J(2010) A parametric empirical Bayesian framework for fMRI-constrained MEG/EEG source reconstruction, Hum. Brain Mapp 31(10):1512��?1531.
- Science Daily-Combat-Related Injuries: Brain Imaging Differences in Veterans With TBI 12-13-2013
- http://brainweb.bic.mni.mcgill.ca/brainweb/
- Science Daily-Combination of Two Imaging Techniques Allows New Insights Into Brain Function 13-08-2013
- Jyothi V, Rajesh Kumar B, Krishna Rao P, Rama Koti Reddy DV (2011)Image Fusion Using Evolutionary Algorithm (GA), Int. J. Comp. Tech. Appl, 2(2):322-326.
- Chen V, Su Ruan (2010) Graph cut segmentation technique for MRI brain tumor extraction, 2nd International Conference on Image Processing Theory Tools and Applications (IPTA), PP:284��?287.
- Wentao W, Cong C (2010) Dirichlet Markov Random Field Segmentation of Brain MR Images, 4th International Conference on Bioinformatics and Biomedical Engineering (iCBBE), PP:1��?4.
- Rasmussen CE, Williams CKI (2006) Gaussian Processes for Machine Learning, the MIT Press, ISBN 026218253X
- Cover TM, Thomas JA (1991) Elements of Information Theory, 2nd edition, John Wiley & Sons, Inc.
- Satpathy A,Jiang X,Eng HL (2010) Extended histogram of gradients feature for human detection. In 17th IEEE InternationalConference on Image Processing (ICIP), PP:3473 ��?3476.
- Angeline Nishidha A (2012) Multi-Focus Image Fusion using Genetic Algorithm and Discrete Wavelet Transform, International Conference on Computing and Control Engineering (ICCCE 2012), p.12.
- Cvejic N,CanagarajahCN, Bull DR (2006) Image fusion metric based on mutual information and Tsallis entropy, IET Electronic Letter, 42:626-627.
- Neural Networks by Rolf Pfeifer, Dana Damian, Rudolf Fuchslin 2012.
- Rybski P, Huber D, Morris D, Hoffman R (2010) Visual classification of coarse vehicle orientation using histogram of oriented gradients features. In IEEE Intelligent Vehicles Symposium (IV), pp:921��?928.
- Xiaolin Hu, Balasubramaniam P (2012) Recurrent Neural Networks:ISBN 978-953-7619-08-4.
- Wang J, Guan H, Solberg T (2011) Inverse determination of the penalty parameter in penalized weighted least-squares algorithm for noise reduction of low-dose CBCT, Med Phys, 38:4066��?72.
- Evans JD, Politte DG, Whiting BR, O��?Sullivan JA, Williamson JF (2011) Noise-resolution tradeoffs in X-ray CT imaging: a comparison of penalized alternating, Med Phys, 38:1444��?58.
- Sui J, Pearlson G, Caprihan A, Adali T, Kiehl KA, Liu J, et al. (2011)Discriminating schizophrenia and bipolar disorder by fusing fMRI and DTI in a multimodal CCA+ joint ICA model. NeuroImage, 57:839��?55.
- Yuan Q, Dong CY, Wang Q (2009) An adaptive fusion algorithm based on ANFIS for radar/infrared system, Expert Systems with Applications, 36:111-120.
Relevant Topics
- Artificial Intelligence and Philosophy
- Automated Reasoning and Inference
- Case-based reasoning
- Cognitive Aspects of AI
- Commonsense Reasoning
- Constraint Processing
- Heuristic Search
- High-Level Computer Vision
- Human Centered
- Human-Robot Interaction
- Intelligent Interfaces
- Mobile Robot System
- Nano/Micro Robotics
- Robotics
- Robotics for Application
- Robotics for Mechanism
- Robotics In Medical
- Sensing and Perception
Recommended Journals
Article Tools
Article Usage
- Total views: 15051
- [From(publication date):
December-2014 - Jan 30, 2025] - Breakdown by view type
- HTML page views : 10541
- PDF downloads : 4510