Fisheries Harbour Development: A Review
Received: 20-Sep-2017 / Accepted Date: 02-Nov-2017 / Published Date: 05-Nov-2017 DOI: 10.4172/2332-2608.1000254
Abstract
Due to ever increasing trade and sea-borne traffic, new fisheries harbours and ports are required to be developed and expended the existing port with deeper and wider approaching channel. If a port is to be developed in the zone of high littoral drift, it is of vital importance to predict its effect on the adjacent shoreline and suggest remedial measures to minimize the adverse effects due to construction of the port. Rapid expansion of human activities in the coastal zone is causing several problems. There are various environmental forces like tides, currents, waves and sediment transports and pollutant transport associated with the coastal processes. This note deals with the forces against development of fisheries harbour and feasibility studies would be carried out for the fisheries planning in the coastal region. Scale model are long being used to study coastal engineering problem. Various models are used in dealing with coastal engineering problems particularly in fisheries harbours. Since last two decades mathematical modeling has become a very efficient tool for studying coastal engineering problem for fisheries harbour. These models are essentially based on conservation of mass and momentum equation. Similar to scale model, there are tidal model as well as wave model. These models can be three dimensional (3D) or two dimensional (2D) depending upon governing equation. It is suggested that the above methodologies should be followed for any development of fisheries harbours in India as well as other countries.
Keywords: Fisheries harbours; Reclamations; Dredging; Hydrodynamics; Shoaling
Introduction
Due to ever increasing trade and sea-borne traffic, new fisheries harbours and ports are required to be developed and expended the existing port with deeper and wider approaching channel. If a port is to be developed in the zone of high littoral drift, it is of vital importance to predict its effect on the adjacent shoreline and suggest remedial measures to minimize the adverse effects due to construction of the port. Rapid expansion of human activities in the coastal zone is causing several problems. For example development of ports, construction of jetties/breakwaters and other structures, reclamations, dredging discharges from industries, thermal/nuclear power stations etc are causing adverse impacts on the coastline. Coastal engineers are associated with these developments in the coastal area. Before these developments, it is necessary to properly plan these developments so as to minimise the adverse effects. Also to protect the coastline from erosion, it is required to construct protective structures in the coastal area. Therefore it is necessary to understand the coastal processes which would help in planning the costal works in a sustainable way. Numerical modeling provides a useful tool for study of hydrodynamics, wave modelling, sediment transport, littoral drift distribution and shoreline changes. The present scenario of the Indian fisheries harbours is to be reviewed because every fisheries harbour is facing problem of siltation, sedimentation/erosion and wave disturbances in the fisheries harbours. The west coast and east coast of India, severe erosion problems is observed all along the coastlines. This editor’s note describes feasibility studies of the existing fisheries harbour and proposed harbours in the above Indian coasts [1-5].
Environmental Parameters of Importance
There are various environmental forces associated with the coastal processes. The following are the important environmental parameters which affect the coastal processes in the nearshore region.
• Waves
• Tides
• Currents
• Wind and storm surge
These environmental parameters are described as follows.
Waves
Waves are generated in the offshore region by the interfacial shear exerted by the wind blowing over the sea surface. The parameters which govern the wave generation process are
Fetch of water surface which is subject to wind (F), Wind Speed (U), Duration of wind (t)
These wind generated waves are important as energy-transfer agents; first obtaining their energy from the winds, transferring it across the oceans and then delivering it to the coastal zones where it can generate variety of nearshore currents and sand transport patterns. The waves are generated due to the transfer of energy from wind to initially calm water surface of sea (seas). After leaving the generation area they propagate towards the coastline without major change in their characteristics (swells). As waves approach the coastline, they undergo transformation due to the processes of refraction, shoaling, diffraction etc. Due to refraction, the wave crests tend to align themselves parallel to the bottom contours. As a result, the wave energy gets concentrated at headlands, whereas the wave energy reduces in the bays the wave height and angle of approach of waves at the coastline play an important role in governing the coastal processes [6-10].
Tides
Tides are defined as the periodic rise and fall of water level in the ocean caused by the gravitational attraction between the celestial bodies. Though many celestial bodies influence the tides, the moon and the sun are the main contributors to the gravitational pull compared to others. Gravitational pull causes water mass in one part of the ocean to rise with corresponding decrease in water level on the other part of the ocean. This rise and fall of water level in ocean is a regular phenomena and occurs daily. The magnitude of the rise and fall of water level at a given location is linked with the relative positions of the moon, the earth and the sun and is influenced further by the geography of the location on the earth. The tides are classified as (i) diurnal (ii) semidiurnal and (iii) mixed. The diurnal tides have one high water and one low water in each lunar day i.e., 24 hours and 50 minutes. The semidiurnal tides occur twice a day with a tidal period of 12 hours and 25 minutes. The mixed tides are characterized by a combination of diurnal and semidiurnal tides. A typical semidiurnal tide. It may be noted that the tidal range is maximum on full moon and no moon days, which are called spring tides. During the first and last quarter of the moon, the tidal range is small, which are called neap tides.
Currents
In the ocean, currents are generated due to various reasons. Some of these which are of concern to coastal engineers are as follows:
a) Ocean circulation
b) Tidal currents
c) Nearshore currents
d) Longshore currents
e) Rip currents
f) On shore – off shore currents.
a) Ocean circulation: Exchange of energy between the atmosphere and the ocean surface is complex. The atmospheric factors which generate circulation in the ocean are, wind and heating of the ocean.
b) Wind driven circulation: The atmosphere receives large solar radiation in the equatorial region compared to the polar region. This differential heating causes air circulation which is influenced by a phenomena known as Coriolis Force.
c) Thermohaline circulation: This is a process which occurs in the deep waters and is caused by the variation in the density of the sea water. This circulation is mainly a convection process wherein the cold water at high latitudes sinks and flows towards the equator. In essence, the major current systems in the oceans are due to the combined effects of wind blowing on the ocean surface and the variation in the density of sea water. The nearshore currents are influenced by ocean currents to some extent.
d) Tidal currents: These currents are generated due to rise and fall of water level caused by tides. The tidal currents play an important role in the coastal processes. In the estuaries and near the river mouths, change in direction of flow every six hours is experienced due to tides. The flow reversal is caused due to rise and fall of water level in sea and the currents generated in the process are known as tidal currents. In addition, tidal currents are quite strong along the region whenever the coastline exhibits drastic change in geometric shape.
e) Nearshore currents: In the nearshore region meteorological factors such as sunshine, wind and precipitation have strong influence on the coastal waters compared to that of deep ocean. Seasonal variations in water temperature, salinity and silt charge are comparatively large in coastal waters. As the coastal waters are influences by fresh water supplied by rivers, the seasonal change in temperature, salinity and silt charge cause density difference and generate currents. In addition, predominant currents in the coastal region are generated due to waves. Depending upon the direction of wave approach, longshore current is generated. The long-shore current continue to occur for some distance along the coast and returns to the sea in the form of rip currents. Also on-shore off-shore currents are generated across the beach which are caused by the waves breaking in the near-shore zone. The strength of these currents depends on the wave characteristics and the beach profile.
Wind and storm surge
As seen earlier, the winds and storms generate waves in the sea, which travel to the coastline and influence the coastal processes. In addition, they cause rise in water level at the coast, which is known as storm surge. Due to the increase in water level at the coast due to the storm surge, higher waves can reach the coastline, which influence the coastal processes.
Coastal sediments
The supply of sediments to the coastal zone is mostly through rivers and partially by disintegration of coastal rock outcrops due to continuous wave action. The sediment budget consists of littoral drift, sediment gain from river sources and cliff erosion, losses down a canyon and shoreward into sand dunes. In addition to the natural supply of sediments, the following human activities accelerate the sediment supply at a particular place.
• Disposal of dredged material
• Pumping of coastal sand for artificial nourishment of coastline.
• Dumping of inland quarried sand for beach replenishment.
Beach processes
The morphological process that the beaches undergo depend upon the interaction between external environmental forces and beach sediments. The beaches adapt their profiles, both transverse and longitudinal, according to the environment. Thus, beach maintains a dynamic equilibrium with the environmental conditions depending on the characteristics of the sediments on the beach.
Longshore transport: In the nearshore region, currents parallel to the shore are generated due to oblique incidence of waves, which are termed as longshore currents Due to energy imparted by the breaking waves, littoral material is transported parallel to the shore, which is termed as littoral drift. The rate of littoral drift (Q) can be computed as follows:
Q (m3/yr)=1290 P
P=pgH2 Cb Sin 2b/16
Where,
ρ=Mass density of water
g=Acceleration due to gravity
H=Wave height
Cb=Celerity of breaking wave
Cb=Breaking wave angle.
The littoral drift is thus a function of wave climate, sediment characteristics, beach profile and configuration of the shoreline. It is seen that on the east coast of India, the general direction of littoral drift is from south to north, which is practically nil at Tuticorin and increases gradually to 1 to 1.5 million cum per year at Paradip. The littoral drift is less on the west coast having magnitude of 0.1 to 0.2 million cum per year and the direction varies depending on the local configuration of the coastline.
Onshore-offshore transport: The sediment transport in transverse direction to the coastline due to wave action is termed as onshoreoffshore transport. This is especially predominant during storms, when high waves are encountered. Onshore-offshore transport of sand associated with profile changes from storm to swell conditions is correlated with the wave steepness H/L, the ratio of the wave height (H) to the deep-water wave length (L). Storm waves have high steepness values, due to both their greater heights and shorter periods, while long swell waves have low steepness values. In general for wave steepness of less than 0.025 (as in fair weather conditions) onshore movement of sand takes place which results in building of beach whereas when wave steepness is greater than 0.025 (as in storm conditions), offshore movement of sand taken place resulting in erosion of the shoreline.
Tidal inlets
A tidal inlet is a waterway connecting the sea and a bay, a lagoon or a river entrance through which tidal and other currents flow. Tidal inlet is a classical example which demonstrates various coastal processes due to the combined effect of waves, tides, currents and wind:
Normally, three major forms of sediment accumulation are associated with ebb-tidal deltas
(a) Asymmetric swash bars, oriented landward and formed by wave action, which form a broken semicircle around the perimeter of the ebb-tidal delta and sometimes meet the shore obliquely on either side of the inlet. They form at the inlets because of a combination of the influence of the ebb-tidal currents, and wave refraction around the lobe, which tends to slow down the transport of sand past the inlet.
(b) Channel margin linear sand bars which are perpendicular to shore and parallel to the main channel.
(c) A lunate, which is formed by the sand deposited seaward of the main channel by ebb currents.
Two different methods of bypassing exist in nature, viz., “bar bypassing” and “tidal flow bypassing”. Most cases of bypassing present combinations of these two general principles. Whether we have predominant bar bypassing or predominant bypassing by tidal flow, seems to depend upon the ratio between littoral drift and tidal flow. If the predominant mean littoral drift (M) is expressed in cubic units per year and the maximum tidal flow under spring tide conditions in the same cubic units per second (Qm), bypassing may be described by
M/Qm=r factor.
with r>200–300 usually bar bypassing results, whereas
with r<10–20 we usually have tidal flow bypassing
The degree of stability of a tidal inlet can be evaluated as follows:
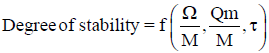
where Ω is the tidal prism and τ is the bed shear stress given by
τ=Pg Q2m/A2C2
which
p=density of water
g=acceleration due to gravity
C=Chezy’s coefficient
A=Area of cross section of tidal inlet
Check for
Ω/M,
Ω/M>300 for high stability
Ω/M<100 rather unstable
Check for
Qm/M,
Qm/M>0.01 generally stable
Qm/M<0.01 less stable.
The value of τ should be 0.4 to 0.6 kg/m2 for stability.
It is seen from the foregoing that the beach is under a state of dynamic equilibrium with the environmental parameters of waves, tides, currents, winds etc which are prevalent in the coastal area. The response of the beach is a function of shoreline configuration, beach profile and sediment characteristics. Also, the coastal processes are influenced by sources/sinks of sediment materials. Thus, the morphological processes in coastal areas are quite complex and need comprehensive understanding of the various coastal processes involved. The coastal engineer has to plan development activities duly considering the coastal processes in that region.
Physical Modelling
Scale model are long being used to study coastal engineering problem. Types of models are used in dealing with coastal engineering problems particularly in fisheries harbours.
Wave model
Wave models are undistorted model usually used to determine wave tranquillity or simulation of littoral current in coastal area.
Tidal model
Tidal models are distorted model used for simulation of tidal phenomena like tidal level, tidal current.
Wave cum tidal model
For simulation of inlet phenomena where both wave and tide are important wave cum tidal model are used. These models are usually distorted.
Wave flume
Wave flumes are used to test breakwater section or any other maritime structure under regular and irregular waves.
Hot water circulation model
As a number of power plants are situated along the coast of India, hot water circulation model are used for these studies. These are usually wave cum tide model having facility of injecting hot water and measurement system of temperature rise.
The scale models used for studying coastal engineering problems are Froudian model. Equality of Froud number both in proto and model is used for deriving model laws – Similarly other model laws can be derived.
Mathematical Modeling
Since last two decades mathematical modeling has become a very efficient tool for studying coastal engineering problem. These models are essentially based on conservation of mass and momentum equation. Similar to scale model, there are tidal model as well as wave model. These models can be three dimensional (3D) or two dimensional (2D) depending upon governing equation. At present for coastal engineering problems mostly two dimensional models are used.
In mathematical modeling, the region of interest are schematised by regular square grids in finite difference method or by irregular triangular grids in finite element method. In natural closed boundary usually no flow condition for tidal flows and reflection coefficient for wave model are provided as boundary condition. At open boundary observed tide or flow (velocity) are used as boundary condition for tidal model. For wave model observed wave (height and period) and wave angle are used as boundary condition.
In tidal model Navier stokes equations are solved to get tidal level, velocity (magnitude and direction) at all interior wet grid points. Instantaneous velocity field are depicted by vector diagram. The water level fluctuation and continuously changing velocity field can be demonstrated through animation. In wave model two equations are solved (i) conservation of wave energy (ii) irrotationality of wave number. As output wave models produce wave height and wave direction. The results are presented both as vector field indicating magnitude of wave height and wave direction at all grid points, Also wave isolines are presented to indicate wave crests and troughs. Besides tidal and wave model sediment transport model, pollution transport model, ship navigation model, ship motion models are also used.
Conclusion
It is concluded that the above methodologies should be followed for any development of fisheries harbours in India as well as other countries.
References
- Manivanan (2008) Water Quality Modelling lakes, streams and Estuaries, NIPA, New Delhi.
- Patil BMR, Manivanan SN, Jha C, Kanetkar KHB (2009) Simulation of shoreline changes to assess impact of proposed port, HYDRO2009 held at CWPRS, Pune.
- Coastal Engineering Manual (2004) Coastal Engineering Research Centre, Viksburg, Mississippi, USA.
- Dean RG, Dalrymple RA (1984) Water Wave Mechanics for Engineers and Scientists. Advanced Series on Ocean Engineering 2.
- Brown S, Ferguson (1958) Manual of Tidal Prediction. Nautical Publishers, Glasgow.
- Central Water and Power Research Station (1984) Feasibility Studies for the Tidal Power Project in the Gulf of Kutchch.
- Open University team (1989) Wave, tides and shallow water processes published by the Open University, England.
Citation: Manivanan R (2017) Fisheries Harbour Development: A Review. J Fisheries Livest Prod 5: 254. DOI: 10.4172/2332-2608.1000254
Copyright: © 2017 Manivanan R. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 4740
- [From(publication date): 0-2017 - Mar 13, 2025]
- Breakdown by view type
- HTML page views: 3941
- PDF downloads: 799
