Rapid Communication Open Access
Evaluation of Molecular Perturbation of a Deuterated Protein by Temperature Factor Refinement in X-Ray Structural Analysis of High- Resolution Diffraction Data
Takuya Uemura1,2, Akiko Kita2 and Yukio Morimoto2*1Graduate School of Science, Kyoto University, Kyoto 606-8502, Japan
2Research Reactor Institute, Kyoto University, Kumatori, Osaka 590-0494, Japan
- Corresponding Author:
- Yukio Morimoto
Division of Quantum Beam Material Science
Research Reactor Institute, Kyoto University
Kumatori, Osaka 590-0494, Japan
Tel: +81-72-451-237
Fax: +81-72-451-2371
E-mail: morimoto@rri.kyoto-u.ac.jp
Received date: April 09, 2016; Accepted date: April 21, 2016; Published date: April 28, 2016
Citation: Uemura T, Kita A, Morimoto Y (2016) Evaluation of Molecular Perturbation of a Deuterated Protein by Temperature Factor Refinement in X-Ray Structural Analysis of High-Resolution Diffraction Data. J Biotechnol Biomater 6:223. doi:10.4172/2155-952X.1000223
Copyright: © 2016 Uemura T, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Biotechnology & Biomaterials
Abstract
Structural analysis of deuterated proteins, which are essential for neutron protein crystallography, involves refinement of X-ray crystallographic data using atomic or molecular thermal stability factors. Analysis of high resolution (~0.9 Å) X-ray data can localize some of the hydrogen atoms in a protein molecule. Thermal stabilities and temperature factors are affected by some reasons; one of them is the masses of hydrogen and deuterium atoms. We propose a method to refine X-ray data, taking into account these effects, to show existence probability for deuterium in the protein. Thermal factors were calculated using several physical parameters, and the resultant values were fitted to the experimental thermal factors with high accuracy. This computational method can be applied to analyze and predict the hydrogen/deuterium exchanged states of protein crystals, even small crystals that are unsuitable for neutron crystallography.
Keywords
Deuterium temperature factor; Protein structure; X-ray crystal analysis; Molecular perturbation
Introduction
It is important in the structural analysis of protein tertiary structures to determine the positions of hydrogen atoms and solvent water. For example, the catalytic sites of enzymes include specific hydrogen atoms that are essential to their catalytic mechanisms. This information has contributed to progress in chemical biology, pharmacy, and medical sciences. Neutron diffraction is a powerful technique to determine the positions of hydrogen atoms in a protein molecule with high precision, although it is necessary to crystallize the deuterated protein because of decreasing incoherent scattering from the many hydrogen atoms in a protein molecule. Exchanged deuteriums behave similarly to hydrogen atoms and their precise positions can reveal processes involved in biological functions. It is important to evaluate the deuterated ratio of the protein in a crystal state before carrying out a neutron experiment, but a protocol with which to estimate this ratio has never been reported.
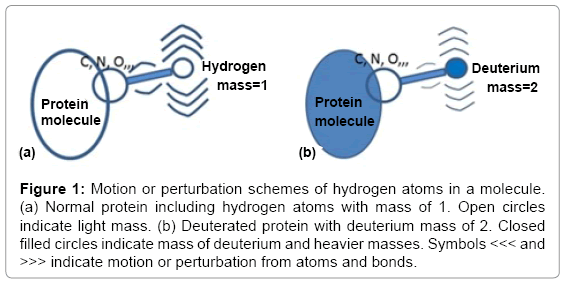
In exchanging hydrogen atoms to deuteriums, protein molecules become heavier, and due to the isotopic effect, chemical bonds involving deuterium will be stronger (Figure 1) [1]. Thus, the motion and/or frequency of a deuterated protein molecule in the crystal condition is lower and the thermal temperature (B) factor, which shows isotropic atomic fluctuations due to thermal effects, B = 8π2Δr2, is reduced [2]. In this report, we propose a method to characterize deuterated protein molecules from the viewpoint of molecular hardness, which is defined by thermal factors using ultra-high resolution X-ray crystallographic data. Using this characteristic of the B factor, we propose a method to estimate how a crystal transferred to a deuterated solvent is really deuterated and to assign the deuterated positions.
Figure 1: Motion or perturbation schemes of hydrogen atoms in a molecule. (a) Normal protein including hydrogen atoms with mass of 1. Open circles indicate light mass. (b) Deuterated protein with deuterium mass of 2. Closed filled circles indicate mass of deuterium and heavier masses. Symbols <<< and >>> indicate motion or perturbation from atoms and bonds.
Materials and Methods
Theory
In X-ray diffraction, the Debye-Waller factor M is related to the B factor as M = B (sinθ /λ)2, where θ is twice as big as the angle between the injection beam and the scattering beam, and ë is the wavelength of the X-ray. Thus, using the approximation of the Debye-Waller factor and the Debye model in crystallography, the B factor is approximated as [3],
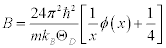
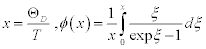 (1)
(1)
where m is mass of a molecule in the unit cell, T is the temperature, and ÈD is the Debye temperature. According to this approximation, the Born-Karman boundary condition may be carefully adopted. In addition, in the following discussion the longitudinal wave and the transverse wave are not distinguished, and it is considered that there is one molecule per unit cell. If there are actually several molecules in a unit cell, they are all treated as one big molecule. Periodic boundary conditions of the crystal are considered, and the maximum angular frequency of the lattice vibration ωD is calculated as
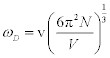 (2)
(2)
where v is the sound velocity in the crystal, N is the number of molecules in a unit cell; N = 1 in this discussion, and V is the lattice volume. The Debye temperature is related to the maximum angular frequency by: 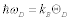 . According to an approximation in the Debye model, the sound velocity is represented as
. According to an approximation in the Debye model, the sound velocity is represented as 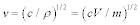 , where c is the elastic modulus and ρ is the density of the unit cell, following the relation of
, where c is the elastic modulus and ρ is the density of the unit cell, following the relation of 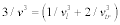 ; l and tr are the longitude and transverse waves. The Debye temperature is written as:
; l and tr are the longitude and transverse waves. The Debye temperature is written as:
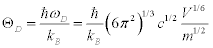 (3)
(3)
When the temperature is significantly higher than the Debye temperature, the formula in the bracket at the right side is approximated as:
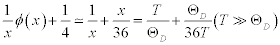 (4)
(4)
From Equation.1, Equation.3 and Equation. 4:
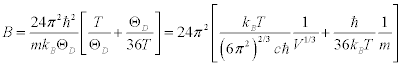 (5)
(5)
Thus, if the temperature is constant, the B factor depends only on the elastic modulus, the molecular mass and the lattice volume.
Crystallization, data collection and refinement
Three types of hen egg-white lysozyme protein crystals were grown. One was in hydrogen water (H-Lys). The other two were denatured and refolded in deuterated solvent; one solvent contained DCl (D-Lys) and another contained NaOD (NaOD-Lys). Later two proteins have some deuterated parts in a molecule, for example dissociable amino acids and/or on the surface. These three proteins were crystallized at 293 K using sitting-drop vapor diffusion. A 2.0 uL aliquotof protein solution at a concentration of 40 mg/mL was mixed with an equal volume of reservoir solution [25% ethylene glycol, 10% NaCl and 100 mM sodium acetate-acetate buffer at pH 4.6]. Crystals grew to full size (0.5 x 0.5 x 0.8 mm) after 1 week. X-ray diffraction data were collected at beamlines BL44XU (Bruker-AXS SMART 6500) at SPring-8 and BL17A (ADSC Quantum 270 detector) at the Photon Factory, Japan. The data were processed using CCP4i:iMOSFLM [4,5] and CCP4i:SCALA [6]. These three crystals all belonged to the tetragonal space group P43212. The data sets are summarized in Table 1. As the starting model of lysozyme, PDB entry 1LYZ was selected [7]. All refinements were carried out using CCP4i:REFMAC5 [8]. The structures were visualized and modified using Coot [9].
| Lysozyme Spring-8 BL44XU |
H-Lys | DCl-Lys | NaOD-Lys |
|---|---|---|---|
| Wavelength (Å) | 0.9 | 0.9 | 0.9 |
| Resolution range (Å) | 33.32 – 0.94 (0.96– 0.94) |
30.77 – 0.90 (0.92 – 0.90) |
33.41 – 0.94 (0.96 – 0.94) |
| Space group | P43212 | P43212 | P43212 |
| Unit cell (Å, deg.) | 78.6 78.6 36.8 90 90 90 |
79.0 79.0 36.9 90 90 90 |
78.9 78.9 36.9 90 90 90 |
| Total reflections | 1,815,518 | 1,822,325 | 1,512,065 |
| Unique reflections | 77,366 (4,524) | 87,610 (4,748) | 78,264 (4,568) |
| Multiplicity | 19.7 (15.6) | 19.6 (14.1) | 17.7 (14.9) |
| Completeness (%) | 99.9 (100.0) | 99.9 (100.0) | 100.0 (100.0) |
| Mean I/sigma(I) | 17.5 (3.9) | 59.0 (4.5) | 957.3 (3.7) |
| Wilson B-factora (Å2) | 8.175 | 7.454 | 7.185 |
| Rbmerge | 0.075 (0.971) | 0.065 (0.788) | 0.096 (0.808) |
| Rcwork | 0.185 | 0.182 | 0.185 |
| Rdfree | 0.208 | 0.194 | 0.200 |
| Number of atoms | 2426 | 2426 | 2426 |
| Macromolecules | 1969 | 1969 | 1969 |
| Ligands | 52 | 52 | 52 |
| Water (oxygene) | 405 (137) | 405 (137) | 405 (137) |
| Protein residues | 129 | 129 | 129 |
| RMS(bonds) (Å) | 0.027 | 0.027 | 0.028 |
| RMS(angles) (deg.) | 2.17 | 2.24 | 2.20 |
Statistics for the highest-resolution shell are shown in parentheses.
aWilson B factor by the Wilson plot computed (ref.11)
bRmerge = Σ (|I-<I>|)/Σ<I>
cRwork = Σ||Fobs|-|Fcalc||/Σ|Fobs|
dRwork is calculated from a set of reflections in which 5% of the total reflections have
been randomly omitted from the refinement and used to calculate Rfree
eNumber of oxygen atoms
Table 1: Data collection and refinement statistics.
Results and Discussion
Three types of lysozyme crystal, H-Lys, DCl-Lys and NaOD-Lys, produced high-resolution data, to 0.9 Å, and each showed typical electron density maps for hydrogen atoms around the main chain and some amino acid side chains. Model building and structural modifications with graphical software can identify the positions of hydrogens around the terminal amino acid residues, nitrogen in the polypeptide-chain and oxygen of water molecules (Figure 2). Results of the three structure determinations indicated 137 water molecules (H-O-H atoms) (Table 1). The crystallographic refinement was done using the scattering length of a hydrogen atom even if a deuterium had replaced the hydrogen.
All of the experiments were carried out at constant temperature, 100 K. The Debye temperature of a globular protein in a powder state is about 13 K [10], so T»Θ_D. In order to calculate m in Equation. 5, the protein particle, ligand and water molecular masses were mathematically added, and since the number of enzymes in the unit cell of the P43212 crystal is 8, the calculated mass was multiplied by 8. For the deuterated protein, however, the number of deuterated hydrogens was set to 260 temporarily, which is the approximate number of dissociable hydrogens in lysozyme. However, this number would not significantly influence the result under this experimental condition. Using Equation. 5, the overall B factors were calculated. The B factors of the three proteins were all about 0.045 Å2. However, the experimental B factors of H-Lys, DCl- Lys and NaOD-Lys from the crystallographic data were 12.811, 12.352, and 11.537 Å2, respectively (Table 2), in which B factors were averaged over all atoms in the protein. Differences in the numerical order were explained by considering that the elastic modulus in this crystal state is different from that of the powder crystal because of the existing water molecules. Considering that the Debye temperature is dependent on the elastic modulus, the Debye temperature of the lysozyme crystal containing water molecules was calculated using the experimental B factor of H-Lys. In addition, it is considered that the deuterated protein is more rigid than the non-deuterated protein [1]. Accordingly, the elastic modulus of a deuterated protein should be higher. As the elastic moduli of deuterated lysozymes were 1.06-1.07 times as large as that of H-Lys, the ratio of calculated B factors of these two deuterated proteins to that of the non-deuterated protein corresponds to the ratio of the experimental B factors (Table 2). Similar result was obtained in an experiment carried out for two crystals of γE-Crystallin, in which X-ray diffraction data were obtained for the non-deuterated protein soaked in hydrogen water and for the non-deuterated protein in deuterium water at 1.45 Å resolution and showed the B factor of the former was greater than that of the later [2]. Results of our experiments indicate that deuterated ratio of protein molecule can be determined using this equation, i.e. by considering how the protein is really deuterated and utilizing the deuterium effect on the elastic modulus.
| Data set | H-Lys | DCl-Lys | NaOD-Lys |
|---|---|---|---|
| Ma (g/mol) | 138849 | 143134 | 143134 |
| m (kg) | 2.3057×10-22 | 2.3769×10-22 | 2.3765×10-22 |
| a (Å) | 78.610 | 78.960 | 78.935 |
| b (Å) | 78.610 | 78.960 | 78.935 |
| c (Å) | 36.790 | 36.875 | 36.870 |
| V (Å3) | 2.2735×105 | 2.2990×105 | 2.2973×105 |
| ΘD (K) | 13 | 12.8 | 12.8 |
| x = ΘD/T | 0.130 | 0.128 | 0.128 |
| Φ/x + 1/4 | 7.70 | 7.80 | 7.80 |
| B (calculated) (Å2) | 4.9×10-2 | 4.9×10-2 | 4.9×10-2 |
| Bb (observed) (Å2) | 12.805 | 12.352 | 11.537 |
| ΘD (corrected) (K) | 0.804 | 0.820 | 0.820 |
| Bhc (corrected) (Å2) | 12.8 | 11.9 | 11.9 |
aTotal mass in the unit cell
bAveraged by individual B factor of atoms in the coordinates
cCorrected by ΘD parameter
Table 2: Concrete values in the equations and evaluated thermal factors.
As the elastic modulus depends on the number of deuterated water molecules, the B factor of the protein will change along with changes in the deuterated ratio. For example, in 50% H2O/50% D2O solvent, the elastic modulus would be at the midpoint between that of the non-deuterated protein and the hydrogen protein soaked in 100% deuterium water. This elastic modulus can be used to estimate the number of deuterated waters in the crystal state and to evaluate the rate of deuteration of the protein. Moreover, this approach may indicate how rigid or flexible protein regions or domains are, by taking into account thermal perturbations and/or stability factor evaluation by analysis of the X-ray diffraction data. It is of course clear that neutron diffraction studies to localize hydrogen or deuterium atoms with high accuracy will allow analyses and clarification of factors affecting structural stabilities using the neutron refinement technique. In the case where only small crystals for neutron diffraction analysis, this deuterium refinement method, which utilizes synchrotron high-resolution data, is available to evaluate molecular perturbations and mobility in structural analyses.
In this model, a number of parameters were implicitly contained in the correction of the elastic modulus, for example, the differences between transverse and longitude waves, the anharmoniceffect, the lattice strain, and so on. Research to accurately determine the deuterium effect on the elastic modulus in the crystal structure should be carried out using other experimental methods. This future research will establish how to accurately evaluate the deuteration rate and the state of hydrogen atoms in protein molecules.
Acknowledgements
This work was supported by the Photon and Quantum Basic Research Coordinated Development Program from the Ministry of Education, Culture, Sports, Science and Technology, Japan (AK and YM), and the Customer Care Plan Foundation (YM), and by the Project Research Foundation (YM) under approvals 27037 and 27040 of Research Reactor Institute, Kyoto University. The synchrotron radiation experiments were conducted under the approvals 2015A6550 and 2016A6649 for SPring-8 and 14G557 and 15G023 for PF, Japan.
References
- Cioni P, Strambini GB (2002) Effect of heavy water on protein flexibility. Biophys J 82: 3246-3253.
- Artero JB, Härtlein M, McSweeney S, Timmins P (2005) A comparison of refined X-ray structures of hydrogenated and perdeuterated rat gammaE-crystallin in H2O and D2O. ActaCrystallogr D BiolCrystallogr 61: 1541-1549.
- Debye P (1913) Interferenz von Röntgenstrahlen und Wärmebewegung. Annalen der Physik 348: 49-92.
- Winn MD, Ballard CC, Cowtan KD, Dodson EJ, Emsley P, et al. (2011) Overview of the CCP4 suite and current developments. ActaCrystallogr D BiolCrystallogr 67: 235-242.
- Battye TG, Kontogiannis L, Johnson O, Powell HR, Leslie AG (2011) iMOSFLM: a new graphical interface for diffraction-image processing with MOSFLM. ActaCrystallogr D BiolCrystallogr 67: 271-281.
- Evans P (2006) Scaling and assessment of data quality. ActaCrystallogr D BiolCrystallogr 62: 72-82.
- Diamond R (1974) Real-space refinement of the structure of hen egg-white lysozyme. J MolBiol 82: 371-391.
- Murshudov GN, Skubák P, Lebedev AA, Pannu NS, Steiner RA, et al. (2011) REFMAC5 for the refinement of macromolecular crystal structures. ActaCrystallogr D BiolCrystallogr 67: 355-367.
- Emsley P, Cowtan K (2004) Coot: model-building tools for molecular graphics. ActaCrystallogr D BiolCrystallogr 60: 2126-2132.
- Edelman J (1992) The low-temperature heat capacity of solid proteins. Biopolymers 32: 209-218.
Relevant Topics
- Agricultural biotechnology
- Animal biotechnology
- Applied Biotechnology
- Biocatalysis
- Biofabrication
- Biomaterial implants
- Biomaterial-Based Drug Delivery Systems
- Bioprinting of Tissue Constructs
- Biotechnology applications
- Cardiovascular biomaterials
- CRISPR-Cas9 in Biotechnology
- Nano biotechnology
- Smart Biomaterials
- White/industrial biotechnology
Recommended Journals
Article Tools
Article Usage
- Total views: 11546
- [From(publication date):
June-2016 - Mar 31, 2025] - Breakdown by view type
- HTML page views : 10611
- PDF downloads : 935