Review Article Open Access
Electromagnetic Radiation in Bio-Tissue: A Numerical implementation
Michele Buonsanti*, Giuseppe Megali and Matteo Cacciola
Department DICEAM University of Reggio Calabria, Italy Via Graziella loc. Feo di Vito 89060 Reggio Calabria, Italy
- Corresponding Author:
- Michele Buonsanti
Department DICEAM University of Reggio Calabria
Italy Via Graziella loc. Feo di Vito 89060 Reggio Calabria, Italy
E-mail: michele.buonsanti@unirc.it
Received date June 12, 2013; Accepted date July 09, 2013; Published date July 18, 2013
Citation: Buonsanti M, Megali G, Cacciola M (2013) Electromagnetic Radiation in Bio-Tissue: A Numerical implementation. J Biomim Biomater Tissue Eng 18:109. doi: 10.4172/1662-100X.1000109
Copyright: © 2013 Buonsanti M, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Biomimetics Biomaterials and Tissue Engineering
Abstract
Wireless personal communication is a rapidly expanding sector, particularly in the field of wireless local area networks. In an indoor wireless network system, an user can be close to the radiating antenna. Therefore, it is important to consider possible health hazards due to this type of exposure. This paper presents an approach to estimate and evaluate the main characteristics, i.e., Specific Absorption Rate and temperature rise, related to human exposure to electromagnetic field radiated by common wireless devices such as Wireless Access Points or Hot-Spot. The assessment is done numerically using two different approaches, respectively Ray-Tracing model and Finite Element Method. The general goal is to provide an efficient and accurate method to assess human head exposure to electromagnetic fields at a frequency of 2.45 GHz and for different types of exposure conditions.
Keywords
Electromagnetic radiation; Wi-Fi; FEM; Specific absorption rate; Bio-Tissue; Indoor
Introduction
In the recent years, wireless personal communications have registered a rapidly expansion particularly in the field of wireless local area networks (WLANs). The existing applications of WLANs are spread spectrum systems operating at the Industrial Scientific Medical (ISM) frequency (2.45GHz) and the Unlicensed National Information Infrastructure (U-NII) (5.5 GHz) [1].
Although this framework has given numerously advantages to people, the steadily increasing use of these new technologies may result in greater radio-frequency (RF) exposure in homes and work places. Health agencies have expressed their concern about cumulative exposure [2]. In this paper we focus our attention on the risks of human head exposure to such devices evaluating some important parameters, i.e., Specific Absorption Rate (SAR) and superficial temperature increasing. In this analysis, it is important to underline that WLAN systems use almost omni-directional antennas.
The user can be close to the radiating antenna, where the Electro Magnetic (EM) field assumes its highest values. As a consequence, it is important to consider the possible health hazard due to such systems and, in particular, to define criteria and thresholds for human safety [3]. Our goal is to verify if actual standards in wireless devices respect the Institute of Electrical and Electronic Engineers (IEEE), International Commission on Non-Ionizing Radiation Protection (ICNRIP) and European Committee for Electro technical Standardization (CENELEC) standards. Thus, our goal is to quantify the absorbed power by a biological organism exposed to a EM field and determine its distribution. For our purposes, we approached the problem in two steps. Firstly, we realized the indoor environment and set antenna specifications to evaluate EM field that propagates inside several scenarios. Afterward, retaining previously results, we exploited a FEM approach for simulating the EM absorption of a human head.
Magneto-Hydrodynamics and Physiological Basic Considerations
Red blood cells are the blood cells responsible for the transport of oxygen from the lungs to the tissues and carbon dioxide from the tissues to the lungs. The hemoglobin contained in the nuclei of red blood cells is the substance that operates this transport, thanks to the iron it contains, which gives these cells their color [4,5]. The iron can be magnetized in two ways, or by contact with a magnet, or effect of an electromagnetic field. As it is known, the red blood cells contain iron atoms.
Consequently it is reasonably safe to assume that red blood cells can be electrified and magnetized, attracting one another, forming one pile and by doing so increasing the ESR. The ESR measures the fluidity of the blood, the higher the ESR, less fluid is blood. When the blood is magnetic, the ESR values rise [6].
Generally, a high ESR is interpreted as the sign of an infection. But in the case of blood the magnetic VES can be high without the presence of any infection. A result of the magnetized blood is both a lower fluidity, and a decrease in its ability to transport energy to the cells, tissues and organs.
The effects of electric and magnetic blood can be different at times with seemingly inexplicable symptoms. It’s opinion of the authors that the investigation of the actions of electromagnetic fields interacting with the human body may allow the acquisition of important information on useful and sensible aspects of human response in circulatory terms.
In other words the flow of blood in the presence of a electromagnetic field gives rise to induced spiral phenomena in the blood vessel of the circulatory system. In fact, the presence of ferrous component within the blood flow determines the magnetism of the same due to external magnetic source which it’s subjected. So, the magnetism causes the vertical motion phenomena that is one the most important aspects in the blood circulation.
In first approximation the sliding blood in the arteries can be described by Poiseuille’s law which relates the flow rate Q of a current of a constant laminar and incompressible fluid in a rigid circular duct with constant cross section through the expression:
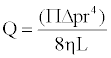 (1)
(1)
Where η is the viscosity while r and L are radius and length of the cylindrical vessel, Δp is the pressure difference at the ends of the duct. Consequently, small changes in radius produce large flow variations.
In the case of vessels, with a diameter greater than 0.5 mm, the viscous behavior blood can be considered as Newtonian type; blood flows as a series of coaxial cylindrical foils, where the central layer has the maximum speed and the most external has zero speed .
The speed u will be parabolic descending from the central axis with it gradient as dv/dr and shear stress τ = η(∂u/∂r). In reality, the blood vessels are not rigid and the blood flow is not constant, but pulsatile.
From the energetic point of view, in every instant, the theorem of conservation allows the conversion of kinetic energy to pressure, depending on the change of section of the vessel. The laminar flow that is typical of the great vessels can become turbulent as it approaches the critical Reynolds number R.
In the micro-circulation blood behaves as a non-homogeneous fluid (likely structured fluid) therefore blood viscosity varies with shear rate and apparent viscosity ηapp is influenced by the temperature of the plasma viscosity, the pH of the concentration of erythrocytes and their size and deformability [5].
For vessels whose diameter is comprised between 500 and 30 μm the value of ηapp decreases with decreasing radius. Either way, the presence of red blood cells, in high concentration, determines the rheological behavior of the blood giving this the character of non-Newtonian fluid.
From the rheology, combined with the non-laminar flow regime, descends a physical picture for an analytical model whose actual behavior is very close to the Beltrami flow model [7]. About this last generally speaking Beltrami flow is defined by ω=λu, where ω is a vector field and normally represents the vorticity field, with velocity field u. The resulting problem solution is hard to obtain since great difficulties appear to Navier-Stokes closed form solution.
Following [7] a coherent approach, with our model, has been compared through helical solution for the free Maxwell equation, representing this the electromagnetic analogy of the Beltrami fields. In [7] the author find, in closed form, stable spherical formations in according to previous experiences in vorticity treating.
Problem Formulation
Electrical properties of biological materials have been a focus of interest since influences of electromagnetic waves are particularly interested by these properties [8-11].
Specifically, human tissues exposed to EM field absorb its energy and are subjected to different effects depending principally on its frequency. We focus our attention on effects produced by high frequency radiations, particularly at 2.45 GHz because of our interest in WLAN applications. The analysis can be consequentially reduced to the determination of 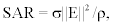 expressing the power absorbed per unit of mass, where σ is the conductivity of human brain tissue, ? the density, and
expressing the power absorbed per unit of mass, where σ is the conductivity of human brain tissue, ? the density, and 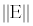 is the norm of the electric field.
is the norm of the electric field.
Studies about the interaction of EM field with human bodies were investigated since '80s when WLAN technology did not exist yet. Advances started in '90s with more performing computers and software [1]. Studies were focused on single parts of human body (e.g., the head) and not to the whole body since high frequency radiations. The main advantages of actual tools are the precise modeling of human head by importing MRI images and setting the parameters of different tissues. In addition, it has to model not only the direct radiation, but also the effects of scattering. FEM approach retrieves accurate results and can be exploited for multi-physics analysis, i.e., for studying the effects of EM field on the SAR and temperature of human heads.
But, in presence of large scenarios, FEM is affected by high computational complexity. In order to decrease the computational load of FEM, we reduced the in-study environment, reproducing indoor scenarios in a Ray Tracing [12,13] based environment, evaluating the EM field propagation and retaining the results for the subsequent FEM based step. Within Ray Tracing based software, we realized wireless antennas by referring to common commercial antennas. Moreover, we evaluated the EM field by placing different fictitious receivers, delimitating a volumetric area in which is supposed to stay the human head. In this way, we consider as much common situations as possible and provided a variety of results (see Table 1). Subsequently, we introduced our results in a FEM based software, where the human head has been imported by SAM Phantom provided by IEEE and IEC in their studies about SAR measurements [14-18]. Here, a cube has been modeled, containing the human head. Suitable boundary conditions have been applied to cube’s surfaces, satisfying the theorem of equivalence [19] and exploiting the Ray Tracing numerical results.
In this way, we have the same EM effects on the head without modeling the whole large scenarios within the FEM software. Thus, Maxwell equations have been exploited to calculate energy filed that invests the head model. Particularly, our model solves the vector Helmholtz equation everywhere in the domain for an imposed frequency:
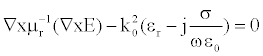 (2)
(2)
Where μr is the relative permeability (1.35 [S/m]), k0 is the freespace wave vector, and εr is the permittivity for a vacuum (56). Constant values of brain tissues have been taken from Schmid studies [20,21]. With this approach, we are able not only to evaluate EM field that invests the head model, but also the EM field inside the head. In this way we can determine also how radiation energy is absorbed by head tissues, thus calculating the SAR values for the head subdomain. The SAR value is an average over a region of either 10 [g] or 1 [g] of brain tissue, depending on national rules. This model does not calculate the average value and so it refers to the local SAR value.
The maximum local SAR value is always higher than the maximum SAR value. In our case, we calculate SAR distribution in the head both on the surface and in depth. To evaluate temperature increases, instead, Bio-heat equation has been exploited [22]:
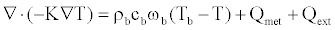 (3)
(3)
where ρb is the blood density, cb the specific heat of blood, ωb the perfusion rate of blood, Tb the blood temperature, Qmet the metabolic thermic source and Qext the spatial thermic source.
| Parameter | Omni-directional | Unidirectional |
|---|---|---|
| Gain | 5.0 [dBi] | 6.0 [dBi] |
| Polarization | Vertical | Vertical |
| E-Plan half-power beamwidth | 100.00 | 105.00 |
| E-Plan first null beamwidth | 170.00 | 165.00 |
| H-Plane half-power beamwidth | 90.00 | 90.00 |
| H-Plane null beamwidth | 180.00 | 180.00 |
Table 1: Parameter imposed for WLAN antenna.
Constant values were previously set referring to Schmid's works [20,21]. Since our multi-physic approach, it has been possible to calculate directly the Qext within the FEM software package by referring to the Joule effect inside the head, exposed to EM radiation. The Bioheat equation models the heating of the head with a heating loss due to the blood flow. This heat loss depends on the heat capacity and density of the blood, and on the blood perfusion rate. The perfusion rate varies significantly in different parts of the human body, and the Table 2 presents the values used in the present work. In order to numerically solve the approached problem, different meshes have been generated with different degrees of accuracy, depending on head sections we were interested in. But, for wave-propagation problem such ours, it is necessary to limit the mesh size according to the problem’s minimum wavelength (typically five elements per wavelength to properly resolve the wave). Our main goal is to verify that the SAR values respect the international ICNRIP standards of 2 [W/kg] for head and body. Then, we want to establish the temperature increase respect to the measured SAR values.
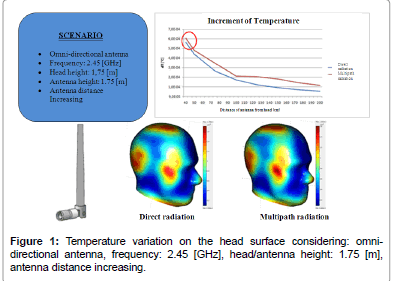
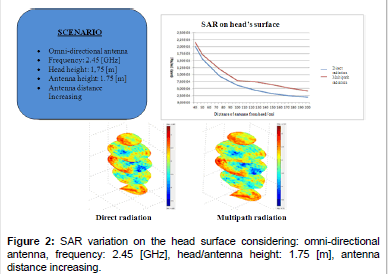
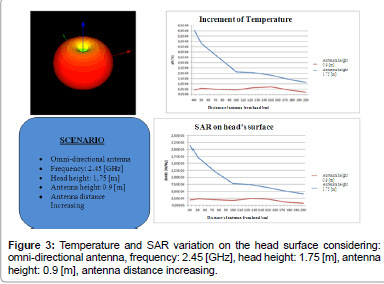
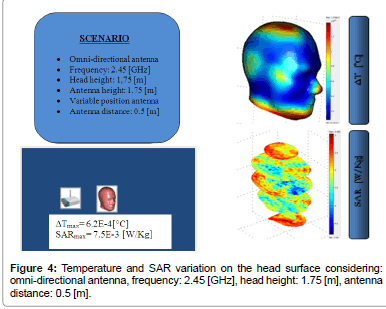
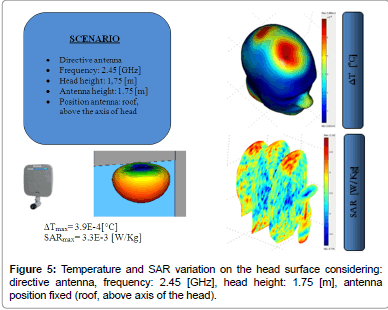
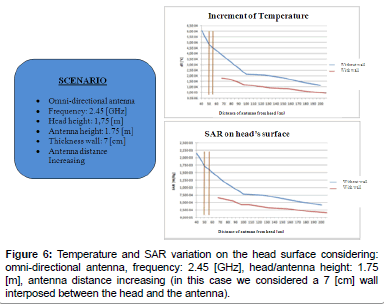
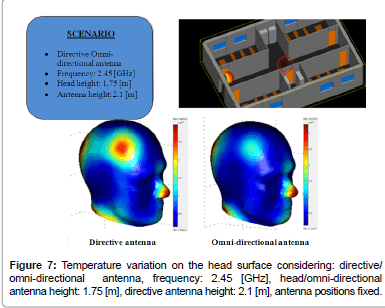
Following figures (please refer to Figures 1-7) show the SAR and temperature variations according with different scenarios simulated and different kind of antenna propagation [22,23].
Generally, SAR distribution in head model and temperature plots draw that the areas where the increase of SAR and temperature are concentrated and where the peak values are reached.
SAR distribution, instead, allow to verify that limits are respected and study how the radiation penetrate in the model. For example, it is possible to see that the radiation penetrate mostly from the side where the antenna is positioned, but other areas are interested in temperature increasing due to the presence of reflected/scattered radiations (by roof or walls). Several simulations were carried out for analyzing the EM effects with the distance between the antenna and the head model. As we expected, in general, temperature and SAR decrease with the distance, and calculated values are influenced by reflected radiation. Particularly, there is a decrement of 4-5*10-4 [°C] for temperature and about 17*10-4-1.5*10-3[W/kg] for SAR.
| Part | Perfusion rate |
|---|---|
| Brain | 2×10-3 [(ml/s)/ml] |
| Bone | 3×10-4 [(ml/s)/ml] |
| Skin | 3×10-4 [(ml/s)/ml] |
Table 2: Parts of human body and relatively perfusion rates.
We also consider the effect due to presence of 7 [cm]-thick brick wall, positioned between the antenna and the head model, in order to simulate the case of two rooms close each other. The presence of the wall causes a decrement of values of 4-5*10-4 [°C] for temperature and 1.5*10-3[W/kg] for SAR, according to the fact that quite part of radiation is absorbed by the wall. Many other cases with antenna positioned in different placed were examined, but never registering values higher than the standard limit. For instance, we examined the case of antenna positioning on a desk close to a user: in this case, simulations showed a temperature increment at the bottom part of the head near the chin, but values do not exceed standard limits.
All these cases are referred to an omni-directional antenna. Considering directive antennas, peaks values of temperature and SAR are positioned in correspondence of axis of maximal directivity. We considered also these cases, showing that calculated values were a little bit higher than the case of omni-directional antenna, and temperature increments are more concentrated in the areas of direct exposure. On the contrary, when user is not positioned in correspondence of the maximum directivity axis, omni-directional antennas have registered values higher than directive ones. For instance, in this last case, at a distance of 2.0 [m], the increment of temperature is 4*10-6 [°C] with a directive antenna and 10-5 [°C] with an omni-directional antenna.
Conclusion
In this study, we analyzed the effects of EM field exposure to human head from WLAN instrumentations like Access-Point or Hot-Spot. Our interest was focused on SAR evaluation and temperature increase due to EM-wave propagation. Based on numerical simulations carried out with a joint Ray-Tracing and FEM based approach, interaction between EM field and head model has been investigated. For this reason, different scenarios have been implemented. The proposed method provides a good overall accuracy in determining these effects, as our simulations demonstrate. Numerical models remarked that the distance between antenna and user is the most important parameter for determining the intensity of SAR and temperature increments as well as the exposed area of the human head. Within this framework, we have analyzed field penetration: the radiation penetrates till 1 [cm] of deepness, especially when the antenna is positioned in front of the user(in this case, the eyes, for their composition, are the organs that absorb most part of radiation).
Anyway, results of our simulations never overcame the thresholds imposed by international laws.
The proposed study shows preliminary results, since we consider general cases. Further improvements could analyze particular situations and investigate other wireless technologies using different frequency ranges, in order to establish the impact on human safety.
References
- Bernardi P, Cavagnaro M, Pisa S (1997) Assessment of the potential risk for humans exposed to millimeter-wave wireless lans: the power absorbed in the eye. Wireless Networks 3: 511-517.
- Kuhn S, Urs L, Kramer A, Kuster N (2007) Assessment Methods for Demonstrating Compliance With Safety Limits of Wireless Devices Used in Home and Office Environments. IEEE Trans on Electromagnetic Compatibility 49: 519-525.
- Bernardi P, Cavagnaro M, Pisa S, Piuzzi E (1998) SAR distribution and temperature increase in an anatomical model of the human eye exposed to the field radiated by the user antenna in a wireless LAN. IEEE Trans on Microwave Theory andTechniques 46: 2074-2082.
- Fung YC (1990) Biomechanics: Circulation, Springer, New York, Vol 3.
- Fung YC (1990) Biomechanics: Motion, flow, stress and growth, Springer, New York, Vol. 2.
- Foster KR, Schwan HP (1995) Dielectric properties of tissues. In: Polk C, Postow E (Eds.), Handbook of Biological Effects of Electromagnetic Fields (2ndedn), CRC Press, 1996.
- Kwang-Hua Chu R (2004) Possible Ball like formations of the Beltrami Flow Field, Meccanica, 39: 181-186.
- Levallois P (1999) Study review of hypersensitivity of human subjects to environmental electric and magnetic field exposure. Report to public Health Institute, California Depart. Health Service.
- Salford LG, Brun AE, Eberhardt JL, Malmgren L, Persson BR (2003) Nerve cell damage in mammalian brain after exposure to microwaves from GSM mobile phones. Environ Health Perspect 111: 881-883.
- Preece AW, Iwi G, Davies-Smith A, Wesnes K, Butler S, et al. (1999) Effect of a 915-MHz simulated mobile phone signal on cognitive function in man. Int J Radiat Biol 75: 447-456.
- Henshaw DL, Ross AN, Fews AP, Preece AW (1996) Enhanced deposition of radon daughter nuclei in the vicinity of power frequency electromagnetic field, International Journal Radiation Biology 69: 25-38.
- Glassner A (1989) In: Academi Press, New York, NY, USA.
- Shirley P, Morley KR (2001) In: Peters AK (2ndedn), New Jersey, USA (2001)
- (1980) International Commission on Radiation Units and Measurements, \Radiation quantities andunits," ICRU Report 33 (Bethesda, MD: ICRU).
- (2003) Electronics Communications Committee (ECC) within the European Conference Postal andTelecommunications Administrations. “Measuring Non-Ionizing Electromagnetic Radiation (9 kHz-300 GHz)".
- (2005) Human Exposure to Radio Frequency Fields From Handheld and Body-Mounted WirelessCommunication Devices-Human Models, Instrumentation and Procedures, Part 1: Procedure to Determine the Specific Absorption Rate (SAR) for Handheld Devices Used in Close Proximityto the Ear (Frequency Range of 300MHz to 3 GHz), IEC 62209 Part 1.
- (2003) IEEE Recommended Practice for Determining the Peak Spatial-Average Specific AbsorptionRate (SAR) in the Human Head From Wireless Communications Devices: Measurement Techniques, IEEE Standard 1528-2003.
- (2001) Basic Standard for the Measurement of Specic Absorption Rate Related to Human Exposureto Electromagnetic Fields From Mobile Phones (300 MHz{3 GHz), CENELEC EN 50361.
- Franceschetti G (1983) Boringhieri, Turin, Italy (in Italian language).
- Schmid G, Neubauer G, Mazal PR (2003) Dielectric properties of human brain tissue measured less than 10 h postmortem at frequencies from 800 to 2450 MHz. Bioelectromagnetics 24: 423-430.
- Schmid G, Neubauer G, Illievich UM, Alesch F (2003) Dielectric properties of porcine brain tissue in the transition from life to death at frequencies from 800 to 1900 MHz. Bioelectromagnetics 24: 413-422.
- Megali G (2011) PhDThesis.
- Megali G, Cacciola M (2012) Mondo Digitale Vol. 44.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 21648
- [From(publication date):
July-2013 - Apr 19, 2025] - Breakdown by view type
- HTML page views : 16976
- PDF downloads : 4672