Effect of Infragravity Waves Oscillations on Formation, Development and Destruction of Beach Cusps at a Strand Coastal Plain Sand in Southeastern Nigeria
Received: 24-Jul-2021 / Accepted Date: 14-Sep-2021 / Published Date: 21-Sep-2021 DOI: 10.4172/2155-9910.1000331
Abstract
An in-depth study on effect of infragravity wave’s oscillations on shoreline morphodynamics was carried out to determine its implications on formation, development and destruction of beach cusps at Ibeno beach along a strand coastal plain sand in southeastern Nigeria. Detail analysis of field data acquired over a neap-spring tidal phase a strand that infragravity wave’s oscillations frequencies ranged from 0.0322 to 0.0067Hz. The effects on the horeline were classified according to the order of harmonic frequencies spectra of wave swash patterns: First, Second, Third and Fourth Harmonics Frequencies respectively. However, it was noted that wave swash of the first harmonics infragravity waves frequencies with the highest spectral energy index (SEI), which ranged from 0.5 to 1.0, formed the bays and displaced sediment from the centre of the bays to the rims of the wave swash which developed into horns. Whereas, backwash processes transported sediment seaward from the centre of the bays and formed a depression accordingly. Moreover, the second and third harmonics infragravity wave’s frequencies broadened the bays. However, interference of the fourth harmonic infragravity waves frequencies with the fifth harmonic (gravity) waves frequencies (0 - 0.033Hz) generated oscillatory and turbulent motions which sorted and winnowed sediments in the bays. While sediment displaced from two adjacent bays converged to form the horn between two bays. Averaged beach cusps wavelength increased and fluctuated between 38.50 and 44.30m. On the other hand, the first harmonic waves frequencies were also observed to be responsible for the destruction of beach cusps during flood tide. Result of beach profile surveys at the horns and bays locations within the studied transect generally showed erosion which is an indication of the fact that beach cusps formation is independent of beach volumetric change.
Keywords: Infragravity waves; Beach cusps; Horns and bays; Accretion; Erosion
Introduction
Beach cusps are crescent and sinusoidal geomorphic depressions on sandy beaches. Topographic development of shoreline into beach or swash cusps is a complex nearshore wave breaking phenomenon and can be attributed to standing infragravity edge waves in which infragravity energy must be in the form of a narrow spectral peak with one edge wave mode [1]. Swash cusps configured the beach through the processes of erosion and accretion into bays and horns [2]. Several field studies in the past such as Short [3] and Wright et al. [4] had attempted to establish the relationship between infragravity waves and beach morphology but unable to identify the type of infragravity energy that could be a prime factor in beach morphodynamics. Moreover, several works such as Bowen and Inman [5], Guza and Bowen [6], and Guza and Thornton [7] have suggested that edge waves are a factor in the formation of beach cusps.
Inman and Guza [2] genetically classified beach cusps into surf zone cusps and swash cusps. The surf zone cusps are formed by the currents of the nearshore circulation which configured the beach in the order of surf zone width. Swash cusps are formed by the waves swash and backwash acting directly on the beach face and berm. ‘Swash cusps scallop the beach into regular forms of horns and bays with wavelengths typically ranging from a few centimeters to about 75m, but otherwise do not change the overall alignment of the beach’. Swash cusps are most common on reflective beaches where the incident waves produce a substantial surge of swash up the beach face. The superposition of swash on incoming waves with the motion of sub-harmonic edge waves produced a systematic variation in runup height along the beach face which in turn produced a periodic erosional perturbation [2].
Moreover, as Bowen and Inman [1], Guza and Bowen [6] attributed the formation of beach cusps to edge waves; Inman and Guza [2] defined edge waves as longshore periodic gravity waves which can be excited by wind generated waves which impinged on a beach. According to Eckart [8] the longshore wavelength, Le, and period, Te, are related thus:
Le = (g/2π) T2e (2n+1) tanβ (1)
Where g is the gravity and n=0, 1, 2 etc., is the mode number. The most easily excited edge wave, and the one with the largest amplitude, is of mode zero (n=0) and is a sub-harmonic of the incident wave, i.e the edge wave has a period twice that of the incident wave, Te =2Ti, where Ti is the incident wave period.
Inman and Guza [2] assumed that the wavelength of cusps generated by edge waves is equal to the longshore separation between run-up maxima of the incident edge wave interaction that formed the initial perturbation along the beach face. Based on the above assumption, the cusps wavelength is equal to one-half of the wavelength of a sub-harmonic edge wave (λe=Le/2), and is equal to the wavelength of a synchronous edge wave (λ=Le). Therefore, the cusps wavelength associated with zero mode sub-harmonic and synchronous edge waves will be given as:
λe =Le/2=(g/n)T2i tan β, sub-harmonic (2)
λe =Le =(g/2n) T2i tan β, synchronous (3)
Where λe is the cusp wavelength measured longshore between cusp apexes [2]
It is quite obvious that cusp wavelength can be predicted mathematically using the above equations but Dean and Maurmeyer [9] noted discrepancies between predicted cusp wavelength and field measurement. It was observed that predicted cusp wavelength was greater than the observed data in the field and attributed to non- planar beach geometry. They had difficulties in accepting edge waves as the causative factor of beach cusp.
But Antia [10] attributed the development and prevalence of beach cusps on Nigerian beaches as a function of beach morphodynamic state, foreshore slope, swash actions and grain-size characteristics of the beaches. Antia [10] asserted that beach cusps played passive role in morphodynamic adjustment of dissipative beaches. It tends to develop during mild coastal condition indicative of seasonal influence and reflective beach state. Moreover, beach cusps seem to form best on beaches that range in sediment size from fine sand to shingle [11].
Beach cusps are called cusplets if the spacing is less than 1.5m or cusps if the spacing is between 1.5m and 25m [12]. However, the findings of Antia [11] revealed that cusps developments and disappearances on sandy beaches along Nigeria coastline have no significant relationship with the direction of beach volumetric change. In fact, the origin of beach cusps is still not well known. Nevertheless, several theories have been proposed to explain the origin of beach cusps. For example, Evans [12] attributed beach cusp development to erosional process while Inman and Guza [2] attributed to the actions of wave swash and backwash on beaches as well as nearshore circulation system in the surf-zone.
Furthermore, knowledge gained from the studies of beach cusp phenomenon has been applied by many investigators in assessment and management of beach erosion and accretion processes [3,5,11,13- 16]. Although the above studies were either theoretical or quantitative however Eliot and Clarke [17] carried out a quantitative but time limited study of cusps dynamics and beach response during a storm event and its associated impact on the beach face of a sheltered sandy beach. Also, Antia [11] noted in his study on cusps development and beach dynamics that 22 and 30% of volumetric erosion and accretion rates respectively were evident during the cusps existence phase than extinction phase.
Therefore, this work attempts to establish the role of infragravity waves on formation, development and destruction of beach cusps and its implications on morphodynamic variability of the shoreline, east of Qua Iboe river estuary, at the coastal plain sand in the southeasten Nigeria.
Study Area
The downdrift shoreline adjoining Qua-Iboe River Estuary is located in Ibeno Local Government Area of Akwa Ibom State, southeastern coast of Nigeria (Figure 1). The shoreline is a mesotidal tropical sandy beach exposed to semi-diurnal tides and southwesterly waves with amplitude less than 20cm, which is associated with southwesterly wind conditions, which vary annually from calm (November-February) through transitional (February-April) to storm weather conditions ( May-October) [18]. Modal wave periods close to the shore are 8 to 12s. Longshore current velocities along the ocean shoreline ranged from 50 to 125cm/s east with periodic reversals to the west at the downdrift beach contiguous to the estuary mouth due to changes in tidal stage [19]. The shoreline represents an exposed section of the abandoned beach ridges laterally bounded by mangrove swamps of the lower Deltaic Plain of Holocene age. It is underlain by Sombreiro-Warri Deltaic Plain Sand of late Pleistocene [20]. The beach is texturally homogeneous with predominantly well sorted fined-grained sand [21].
Materials and Methods
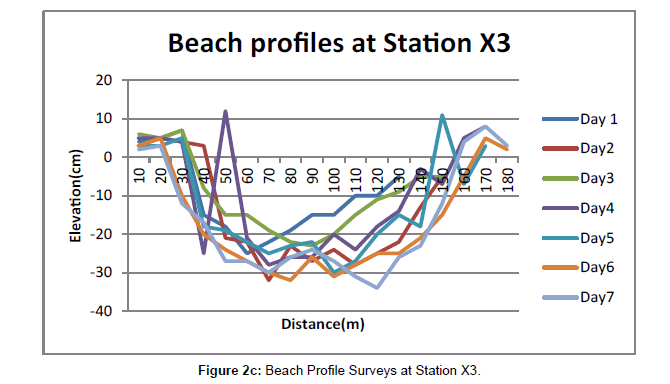
The study covered a period of seven days from August 24 (neap tide) through 30 (spring tide) in 2015. The main monitoring station for this study was established at 500m location at a bay between two beach cusps at Station X3 (Figure 1) with the following geographic coordinates: Longitude 70 591.4011 E and Latitude 40 321 3011 N. However, a total of five consecutive beach profile stations, three at the bays and two at the horns were established within a-100m wide study transect at the shoreline and denoted as stations X1, X2, X3, X4 and X5. Full monitoring of field parameters within fifteen (15) minutes intervals per hour were made on the days of neap and spring tides respectively. These parameters included wave breaker height and water depth, current velocities, breaker types, wave swash frequencies, beach profiles, etc. Daily beach profiles were made at the stations over a near-spring tidal phase, while linear beach profile measurements were converted to beach volumetric change. Details of wave swash oscillations spectra and other hydrodynamic parameters at the stations are presented in Udo-Akuaibit [22].
Result and Discussion
Beach cusps parameters
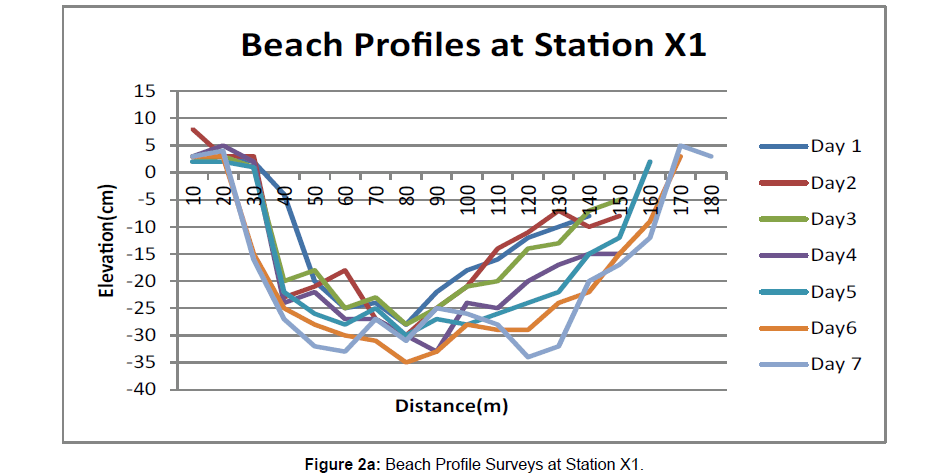
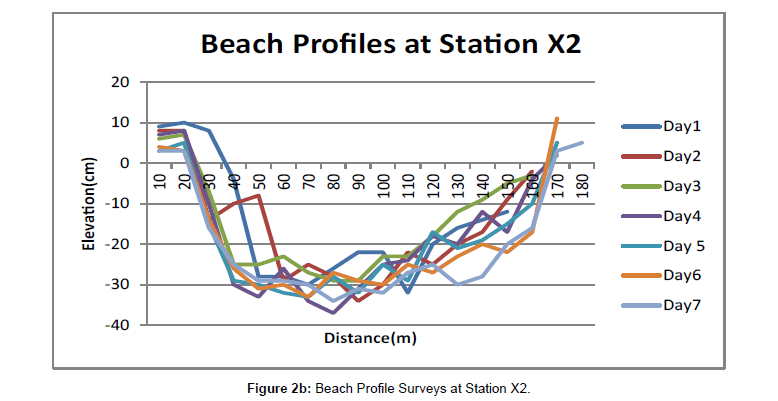
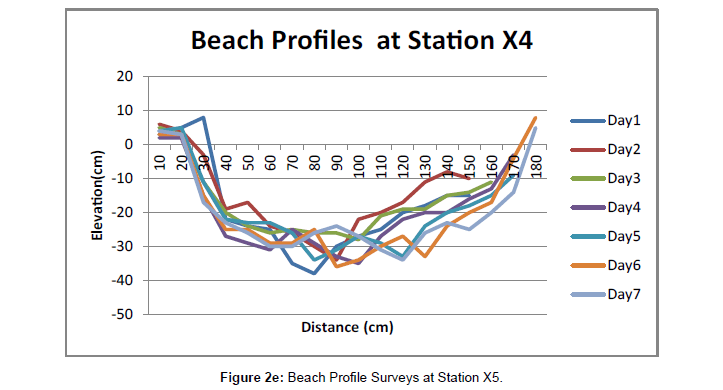
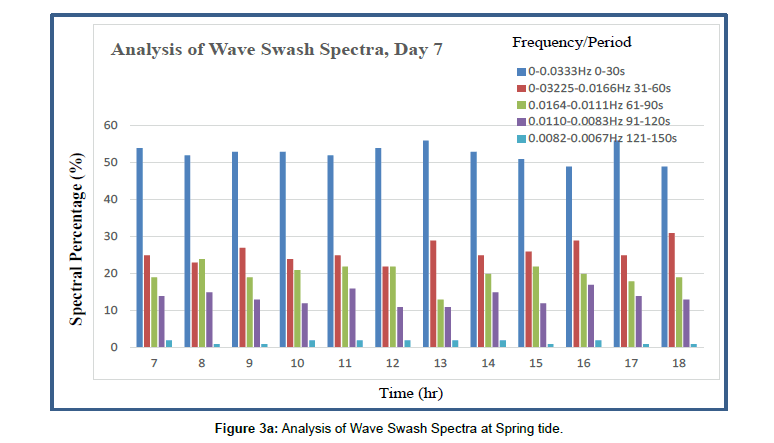
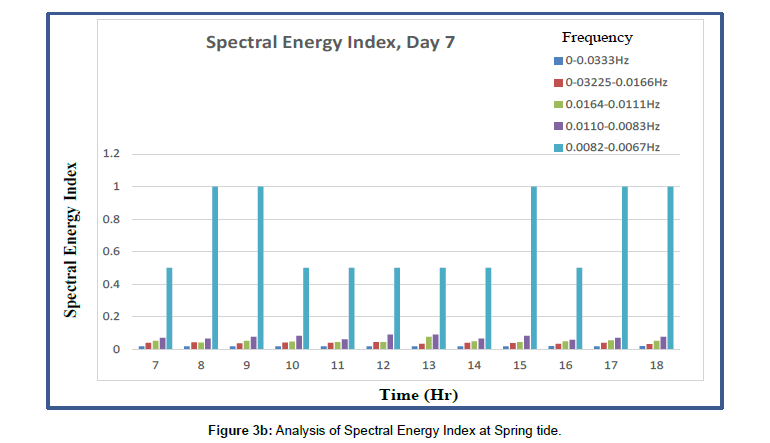
Upper levels of beach cusps were prevalent at the study area. Cusps wavelengths varied between 38 and 44m. Swash length varied and increased from 10 to 70m. Beach foreshore slope ranged from 1 to 50. Net beach sediment volumetric changes were -1.43m3 -1.84m3, -1.54m3,-2.68m3 and -1.89m3 at stations X1, X2, X3, X4 and X5 respectively (Figures 2a, b, c, d and e). Beach profile results showed that the 100m wide study transects generally experienced erosion. The stations X1, X3 and X5, being the bays, recorded a higher degree of erosion than stations X2 and X4 being the horns. Infragravity waves spectrum filtered into frequency groups of first (0.0082-0.0067Hz), second (0.0110-0.0083Hz) third (0.0164-0.0111Hz) and fourth (0.03225-0.0166 Hz) harmonics as well as the fifth harmonic (gravity) waves frequencies (0 - 0.033Hz) as shown in Figures 3a and b [22] played significant role in the formation, development and destruction of beach cusps at the study area.
Formation of beach cusps
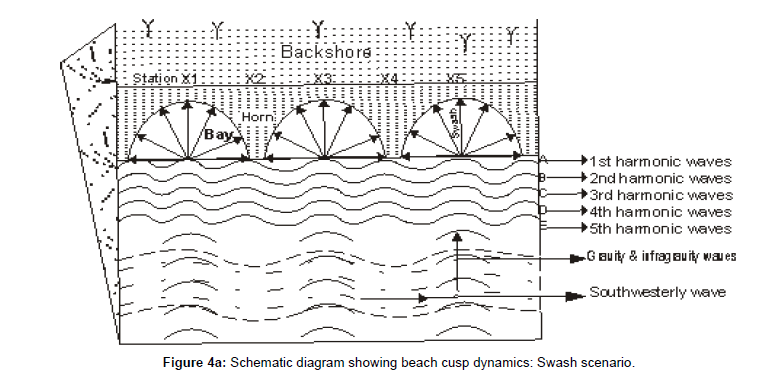
It was observed in the field that wave swash of the first harmonics (0.0082-0.0067Hz) infragravity waves frequencies with the highest spectral energy index (SEI) range from 0.5 to 1.0 as shown in Figures 3a and b [22] formed the beach cusps in which the shapes represented the wave swash geometry on the beach face. So, as the southwesterly waves, parallel to the shoreline, propagated towards the east like edge waves, wind generated infragravity and gravity waves transformed northward towards the shoreline, across the southwesterly waves, which at breaking, mostly plunging breakers, produced wave swash which configured the beach surface into cusp-like shape at a regular interval on the upper foreshore -berm region (Figure 4a). The cusps wavelengths synchronized with that of the southwesterly waves. It was also observed that the cusps bay opened and aligned to the crest of the shore parallel southwesterly waves in the surf zone while the horns pointed towards the trough of the southwesterly waves. The beach cusps formed sequentially in the order of stations X1, X2, X3, X4 and X5 respectively, towards the east in the direction of propagation of southwesterly waves in the surf zone. The second harmonic wave frequency swash preceded wave swash processes of the first harmonic waves group in the formation of beach cup.
Development of beach cusps
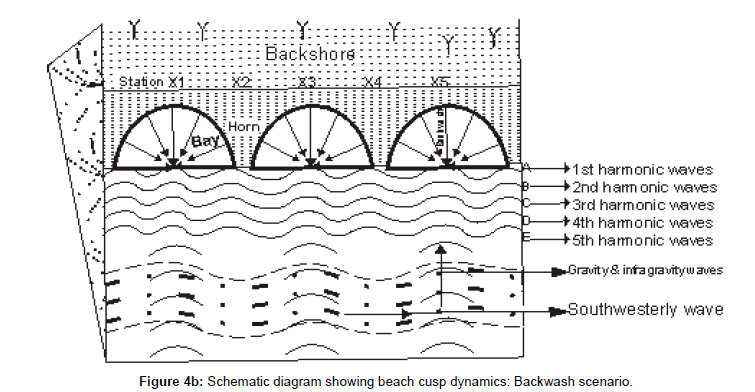
The development of beach cusps is controlled by the third and fourth harmonics infragravity waves swash processes. Waves swash of the first and second harmonics waves frequencies formed the beach cusps, while the third harmonic wave spectrum developed the cusps formed by the first harmonics. The interferences and superposition of wave’s swash of the third harmonics wave frequencies with and over the backwashes of the first and second harmonics generated turbulent and oscillatory motions at the centre of the bay at the mid foreshore. Sediment transported by the backwash of the first and second harmonics from the bays to mid foreshore generated turbulence in which the sediment is transported as undertow to the sea and /or alongshore by longshore currents forming a shallow depression at the centre of the bay (Figure 4b). The fourth harmonics waves inundated and developed the cusps through continuous swash and backwash actions. The interference of the backwash of the third harmonics with the wave swash of the fourth and fifth harmonics waves during midflood to high tide winnowed sediment and consolidated the cusps surface area. However, during ebb tide, the cusps surfaces are exposed by the impact of the first harmonics. It is the swash impact of the first harmonics that formed the cusp during flood tide and the last to impact on the cusp surface during ebb tide forming the cusps final crescent shape which depicted the geometry of the wave swash. The impact of the waves swash on the beach surface transported sediment from the centre of the swash and deposited at the landward fringes of the swash marks towards the berm edge and alongshore fringes to form the horns. Eventually, the associated backwash reduced in volume and flow energy due to water percolation into the beach, transported small quantity of sediment from the crescent outline towards the Centre of the cusps and finally transmitted shoreward as undertow and developed the bay. The horns are developed as a result of convergence of adjacent wave swash actions and deposition of sediment at the point of convergence. Beach cusps are well developed and exposed during ebb tide.
Destruction of beach cusps
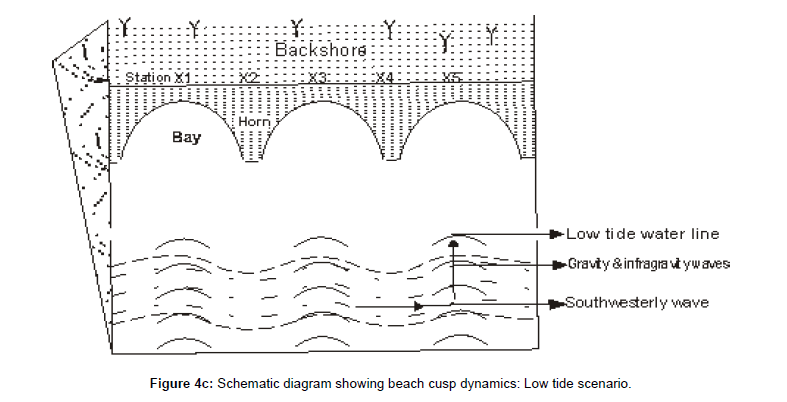
Beach cusp destruction is a complex shoreline processes. The first harmonic waves frequencies formed and destroyed beach cusps. Every preceding wave swash during flood tide superimposed on the former beach cusps formed by the previous wave swash and thereby destroyed the previous ones and formed new cusps. This resulted in a reworking and relocation of the cusps from the lower foreshore during rising tide to the upper foreshore - berm area of the beach. However, beach cusps are inundated and destroyed at high water and poorly developed during flood tide. Similarly, the accelerated neap-spring tidal phase favoured more of deformation and destruction than formation of beach cusps due to complete tidal inundation of the beach foreshore at spring tide. On the contrary, formation and destruction of beach cusps are a continuous process during mid-flood tide while ebb tide is dominated by formation process hence the exposure of beach cusps at low tide (Figure 4c).
Implication of infragravity waves on beach cusps morphodynamics
Beach cusp formation, development and destruction processes are intertwining. This investigation is in support of the findings of Inman and Guza [2] and Antia [10] which attributed beach cusp development to the actions of wave swash and backwash on beaches as well as nearshore circulation system in the surf-zone. Also, this work posits that the wave swash and backwash action which formed beach cusps are generated by the First Harmonic Infragravity Waves Frequencies while southwesterly waves in the surf zone constituted the nearshore circulation system. The eastward sequential trend of formation of beach cusps with northward pointed crescent crests, tangential to the berm edge, are in congruent with the directions of propagation and impact of the southwesterly waves and infragravity wave energy in the surf zone circulation system. It was noted that during the propagation of the southwesterly waves through the surf zone, the crests of the waves aligned with the bays while the troughs aligned with the horns of the beach cusps (Figure 4a). However, the occurrence of beach cusps in this study segment of the beach revealed erosion, given by the net beach sediment volumetric change, and corroborated the findings by Antia [11] and Antia and Nyong [17] that beach cusp played passive role in morphodynamic adjustment of beaches. Moreover, the absence of lower level beach cusps can be due to the flat nature of the foreshore, in which slope varied between 2 and 40. Also, the flat lower-and mid –foreshore of the beach facilitated swift wave swash motions across the lower foreshore to the upper foreshore creating swash marks which developed into beach cusps [22].
Conclusion
Beach cusps formation, development and destruction are a complex shoreline processes controlled by infragravity waves oscillations, beach slope, beach sediment characteristics and nearshore circulation system. The swash and backwash processes of the first harmonic infragravity waves frequencies, with spectral energy index range from 0.5 to 1.0, generated by southwesterly waves circulation system in the surf zone are responsible for the formation and destruction of beach cusps, while their (cusps) developments are controlled by swash and backwash processes of other harmonic waves frequencies in the wave spectra. Therefore, by implication, beach cusps dynamics played significant role in morphodynamic adjustment of the beach.
Acknowledgements
This research did not receive any grant from funding agencies in the public, commercial, or not-for-profit sectors. The assistance of the following personnel in the field: Gabriel Udo-Akuaibit, Uduak Akpan and Ndifreke Gabriel are highly appreciated.
References
- Norhem CA, Herbers THC (1998) Non-Linear evolution of surface gravity wave spectra on a beach. J Phys Oceanography 28: 1534-51.
- Rhie J, Romanowicz B (2004) Excitation of Earth’s continuous free oscillations by atmosphere-ocean-seafloor coupling. Nature 431: 552-6.
- Dolenc D, Romanowicz B, Stakes D, McGill P, Neuhausser D (2005) Observations of infragravity waves at the Monterey ocean bottom  broadband station (MOBB). Geochem Geophys Geosyst 6: Q09002.
- Tanimoto T (2005) The oceanic excitation hypothesis for the continuous oscillation of the Earth. Geophys J Int 160: 276-88.
- Webb SC (2008) The Earth’s hum: the excitation of Earth normal modes by ocean waves. Geophys. J Int 174: 542-66.
- Munk WH (1950) Origin and generation of waves. Proceedings 1st International Conference on Coastal Engineering, Long Beach, California. ASCE: 1-4.
- Tucker M (1950) Surf beats: Sea waves of 1 to 5 minute period, Proc R Soc London Ser A 202: 565-73.
- Munk W, Snodgrass F, Carrier G (1956) Edge waves on the con tinental shelf. Science 123: 127-32.
- Elgar S, Herbers THC, Okihiro M, Oltman-Shay J, Guza RT (1992) Observations of infragravity waves. J Geophys Res 97: 15573-7.
- Bertina X, Bakkera A, Dongerenc A, Cocod G, Andrée G, et al (2018) Infragravity waves: From driving mechanisms to impacts. Earth-Sci Rev 177: 774-99.
- Rawat A, Ardhuin F, Ballu V, Crawford W, Corela C, Aucan J ( 2014) Infragravity waves across the oceans. Geophys Res Lett 41: 7957-63.
- Crawford W, Ballu V, Bertin X, Karpytchev M, (2015) The sources of deep ocean infragravity waves observed in the North Atlantic ocean. J Geophys Res 120: 5120-33.
- Smit PB, Janssen TT, Herbers THC, Taira T, Romanowicz BA (2018) Infragravity wave radiation across the shelf break. J Geophys Res: Oceans 123: 4483-90.
- Fiedler JW, Brodie KL, McNinch JE, Guza RT (2015) Observations of run up and energy flux on a low-slope beach with high-energy, long-period Ocean swell. Geophys Res Lett 42: 9933-41.
- Inch K, Davidson M, Masselink G, Russell P (2017) Observations of near shore infragravity wave dynamics under high energy swell and wind-wave conditions. Continental Shelf Res 138: 19-31.
- Bertin X, Martin K, Baker T, Chataigner T, Guerim T, et al. (2020) Energy transfers and reflection of infragravity waves at a dissipative beach under storm waves. J of Geophys Res Oceans 125.
- Hollman RA, Bowen AJ (1984) Longshore structure of infragravitywave motions. J of Geophys Res 89: 6446-52.
- Kobayashi N, Karjadi E (1996) obliquely incident irregular waves in surf and swash zones. J Geophys Res 101: 6527-42.
- Yasso WE (1965) Plan geometry of headland bay beaches. J Geology 73: 702-13.
- Udo-Akuaibit SP (2014) Sediment Budget Analysis for Sustainable Shoreline Protection and Management. J Geol Geosci 3: 170.
- Centre for Environment and Development in Africa-Ceda (1997) Coastal profile of Nigeria.
- Awosika LF (1992) Cited in Coastal Profile of Nigeria. Centre for Environment and Development in Africa-Ceda 1997.
- Balsillie JH, Carter RWG (1984) The visual estimation of shore- breaking wave height. Coastal eng 8: 367-85.
- Udo-Akuaibit SP (2017) Sea-Level Rise and Coastal Submergence along the South-East Coast of Nigeria. J Oceanogr Mar Res 5: 172.
- Antia EE (1995) Tidal range-related reversal in grain size pattern on tropical sandy beaches of S.E. Nigeria. Senckenbergiana martima 25: 147-53.
- Asangwe CK (1993) Issues and problems in controlling the threats of erosion along the Nigerian coastline: Coastline of West Africa (ed. Awosika, L.F., Ibe. A.C. and shroader, P,) American Society of Civil Engineers, New York: 309-24.
- Ibe AC, Antia EE (1983) Preliminary assessment of the impact of erosion along the Nigerian Shoreline. Nigerian Inst Oceanography and Mar Res, Technical Paper: 18.
- Ibe AC (1988) Coastal erosion in Nigeria. Ibadan University Press, Ibadan: Nigeria.
- Antia EE (1998) A short-term study of the effects of the changing coastal condition on some geomorphic elements on Nigerian beaches. Zeitschrift f. Geomorphologie 73: 1-16.
- Short KC, Stauble AJ (1967) Outline geology of the Niger Delta. American Ass of Pet Geol Bul 51: 761-9.
- Udo SP (2002) Estuarine Shoreline Erosion Dynamics: Case Study of Qua-Iboe River Estuary,S.E. Nigeria. P.G.D.C.Z.M. A Research Thesis, Department of Physical Oceanography, Institute of Oceanography, University of Calabar, Nigeria.
- Hollman RA, Guza RT (1984) Measuring run-up on a natural beach. Coastal Engineering 8: 129-40.
- Longuet-Higgins M, Stewart R (1962) Radiation stress and mass transport in gravity waves, with application to surf beats. J Fluid Mech: 13.
- Herbers THC, Elgar S, Guza RT (1995) Generation and propagation of infragravity waves. J Geophys Res 100: 24863-72.
- Okihiro M, Guza RT (1995) Infragravity energy modulation by tides. J Geophys Res 100: 16143-8.
- Rabinovich AB (2009) Seiches and harbor oscillations. In: Kim, Y.C. (Ed.), Handbook of Coastal and Ocean Engineering. World Scientific Publ, Singapore. 193-236 (Chapter 9).
Citation: Udo-Akuaibit SP (2021) Effect of Infragravity Waves Oscillations on Formation, Development and Destruction of Beach Cusps at a Strand Coastal Plain Sand in Southeastern Nigeria. J Marine Sci Res Dev 11: 331. DOI: 10.4172/2155-9910.1000331
Copyright: © 2021 Udo-Akuaibit SP. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 2791
- [From(publication date): 0-2021 - Nov 29, 2025]
- Breakdown by view type
- HTML page views: 2071
- PDF downloads: 720