Comparison of MLP-ANN Scheme and SDSM as Tools for Providing Downscaled Precipitation for Impact Studies at Daily Time Scale
Received: 28-May-2018 / Accepted Date: 05-Jun-2018 / Published Date: 12-Jun-2018 DOI: 10.4172/2157-7617.1000475
Abstract
Statistical downscaling has become an important part in most of the watershed scale climate change investigations. It is usually performed using multiple regression-based models. Basic working principle of such models is to develop a suitable relationship between the large scale (predictors) and the local climatic parameters called predictands. The development of such relationships using linear regression becomes very challenging when the local parameter to be downscaled is complex in nature such as precipitation. For this reason, use of nonlinear data driven techniques including Artificial Neural Networks (ANNs) is becoming more and more popular. Therefore, an attempt has been made in the study presented here to introduce a new Multi-Layer Perceptron (MLP) ANN-based scheme to develop a robust predictors-predictand relationship to be used as a downscaling model at daily time scale. The efficiency of this model has been compared with a popularly used model called Statistical Down Scaling Model (SDSM), for daily precipitation at the Clutha watershed in New Zealand. The results show that the model developed based on ANN scheme exhibits better performance than the SDSM. Hence, it is concluded that the use of artificial intelligence techniques such as ANN can greatly help in developing more efficient predictor-predictand models for even for precipitation being the toughest climate variable to model
Keywords: Parameters; Hydrological; Neurons; Statistics
Introduction
Global Climate Models (GCMs) are recognized as the most sophisticated tool for producing global scale climate change projections but have limited suitability for regional scale hydrologic impact assessment studies [1,2]. This is because spatial resolution of the GCMs is still too coarse to provide reliable information of local/regional scale climatic variables, especially daily precipitation. Hence, assessing hydrological impacts of climate change requires preprocessing GCM information through the use of a suitable downscaling scheme to generate climate input for the hydrological model being used. There are two broad classes of downscaling that normally appear in literature i.e., statistical and dynamical, and a number of studies provide comprehensive reviews on these two classes such as [1,3-6]. Focusing on statistical downscaling methods, based on their working principle these are of three major types namely; weather generators, weather typing and transfer function or multiple regression [4,7]. Multiple regression based statistical downscaling techniques have been reported to be the most popularly used [8]. These involve the large scale climatic parameters (predictors) and the local variables (predictands; such as temperature and precipitation) and develop a suitable relationship between them, with or without the involvement of principle component analysis (e.g. Schoof and Pryor) and/or the canonical correlation analysis [9] as a data pre-processing technique to simplify the process of regression [10,11]. Owing to its highly stochastic nature, precipitation modelling is always a tough task. Therefore, simplistic, linear regression-based methods may underperform to find an efficient predictor-predictand relationship when the predictand is precipitation. In such situations, soft computing/artificial intelligence techniques have recently shown promise in non-linear regression for developing downscaling models. Artificial Neural Networks (ANNs) is one such option, becoming more and more popular [12-15]. Some more recent studies have presented the application of ANN for downscaling precipitation of a watershed, at monthly time scale [8,16].
The study presented here is an improvement over the existing similar work in multiple ways. Firstly, for downscaling daily precipitation at the Clutha watershed in New Zealand, a new nonlinear multiple regression model developed for this study based on Multi-Layer Perceptron (MLP) ANNs is presented here. Secondly, the modelling time scale of this study is daily which offers more advantage over monthly or seasonal scale that most very recent similar studies work on multilayer perceptron neural network for downscaling rainfall in arid region of Baluchistan [16]. Thirdly, the present study compares MLP-ANNs based model with a popular contemporary method known as Statistical Down Scaling Model (SDSM) in terms of developing a suitable predictor-predictand relationship. In this way, this study will contribute to benchmarking of ANN downscaling models against well-established regression based downscaling models which will help in achieving more efficiency and reliability in precipitation downscaling studies.
Study site and data
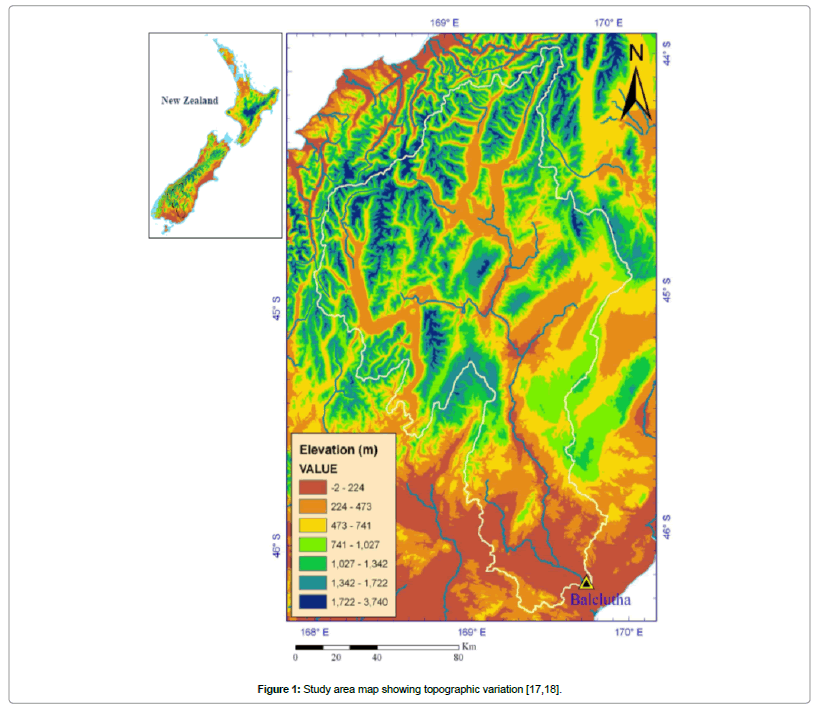
The study site for the modelling work presented here is the same as was described [17,18] i.e., the Clutha River watershed at Balclutha (river gauge) in the South Island, New Zealand (Figure 1). The obvious reason for this is availability of the required data to the authors due to their previous published work pertaining to this watershed. Also, as the Clutha River is the largest river by volume and the second longest river in New Zealand, it has a high national socio-economic value and any new scientific exploration for this watershed is considered important [17,18] provide greater details about the study watershed.
Research Methodology
The structure of ANN used in the study is based on the MLP. The MLP of this specific study has been built up through a network of neurons as its computational elements, interconnected by connection pathways, arranged in a series of layers. In the MLP of this study, there are three neuron layers:
(i) The input layer;
(ii) The output layer; and
(iii) The hidden layer between the input and output layers.
The input layer receives the external input array in a way that each input element is assigned to only one neuron. In this study, the elements of the external input array are the same ten final selected predictors used for constructing a multiple linear regression model using SDSM [17]. This choice of the elements external input array facilitates comparison of like with like to the possible extent between SDSM and ANN. The input neuron conveys its external input without any transformation to each of the hidden layer neurons. Thus, each neuron in this hidden layer has an input array consisting of the outputs of the input layer neurons. Each hidden layer neuron produces only a single output which becomes an element of the input array to each neuron in the subsequent (output) layer. In the present study, as there is only one predictand (precipitation) therefore, the output layer has only one neuron, which produces the final network output in the form of daily precipitation time series. Similar to other studies [19] the optimum number of hidden neurons is found through a trial and error. For this study, it came out to be two (02) neurons beyond which no significant improvement was observed.
As reported by Fernando et al. [19], the process of input-output transformation is transfer function based and is very similar for both hidden and output layer neurons given in Eq. 1. It is basically a "nonlinear transformation of the total sum of the products of each of its input array elements with its corresponding weight plus a constant term".
The weights and the threshold values are basically parameters of the network, which are estimated by calibration/training. This calibration process is achieved by minimizing the least squares objective function using non-linear optimization algorithms [19].
As explained in comparison of two data-driven approaches for Daily River flow forecasting [19], the transfer function used in conjunction with neurons in the hidden and the output layers is the hyperbolic tangent function. The function has an ‘S’ shape and its range varies between -1 and 1, which implies that the estimated network output values are likewise bounded within this range (-1,1). As the actual observed precipitation values are usually outside this range, rescaling of these precipitation values is required in order to compare the actual observed precipitation and the final output time series of the network. In the present study, linear scaling is adopted.
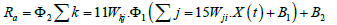 (1)
(1)
where i, j, k = the input, hidden, and output layers, respectively; Ra = the areal rainfall (mm); Φ1 (.) = the linear sigmoid transfer function of hidden layer; Φ2 (.) = the linear sigmoid transfer function of output layer; Wkj = the connection weights between the hidden and output layers; Wji = the connection weights between the input and hidden layers; X(t) = the time series data of input variables; B1 = the bias in hidden layer; and B2 = the bias in output layer.
In line with the similar studies [18], evaluation of the model performance was carried out based on the calculated values of two well-known statistics: (1) Root Mean Square Error (RMSE); and (2) Coefficient of Determination (R2) between the observed daily precipitation data and the model simulated precipitation data for the training and testing data periods. The period of 1961 to 1990 was termed as model training period, which, in climate impact studies is conventionally taken as the baseline period. Also, such a long training period helps proper learning of the model which is considered essential for efficient working of an artificial intelligence scheme such as ANNs. Hence, after achieving satisfactory level of model training (highest R2 and lowest RMSE), its efficiency was tested by inputing the data of 1991 to 2000 period (testing period).
To gauge performance of the ANNs based tested/validated model developed for this study, it was compared with the results of a previously published study by Hashmi et al. [17] for the SDSM downscaling model (a well-known and widely used linear regression based downscaling model) in terms of the values of the two statistics used for model performance evaluation (i.e., R2 and RMSE) and observed versus simulated scatter plots. This is quite in line with the similar studies on introducing new downscaling model published earlier [18], Full details about the SDSM are available in the study of Wilby et al. [4].
Results and Discussion
As mentioned earlier, both the SDSM and the ANNs baed model used the same set of ten (10) large scale predictors in the calibration/ training of their final models. Table 1 shows the full list of twenty-six (26) large scale predictors acquired for the study presented by Hashmi et al. [17]. The ten predictors used in the final SDSM model and the ANNs based model are shown in bold text in Table 1. Full description of each of the 26 predictors is available in the study of Hashmi et al. [17].
| S. No | Predictor Name | S. No | Predictor Name |
|---|---|---|---|
| 1 | ncepmslpaz | 14 | ncepp500az |
| 2 | ncepp5_faz | 15 | ncepp850az |
| 3 | ncepp5_uaz | 16 | ncepp__faz |
| 4 | ncepp5_vaz | 17 | ncepp__uaz |
| 5 | ncepp5_zaz | 18 | ncepp__vaz |
| 6 | ncepp5thaz | 19 | ncepp__zaz |
| 7 | ncepp5zhaz | 20 | ncepp_thaz |
| 8 | ncepp8_faz | 21 | ncepp_zhaz |
| 9 | ncepp8_uaz | 22 | ncepr500az |
| 10 | ncepp8_vaz | 23 | ncepr850az |
| 11 | ncepp8_zaz | 24 | nceprhumaz |
| 12 | ncepp8thaz | 25 | ncepshumaz |
| 13 | ncepp8zhaz | 26 | nceptempaz |
Table 1: List of the NCEP reanalysis predictors used for model training/calibration [17,18].
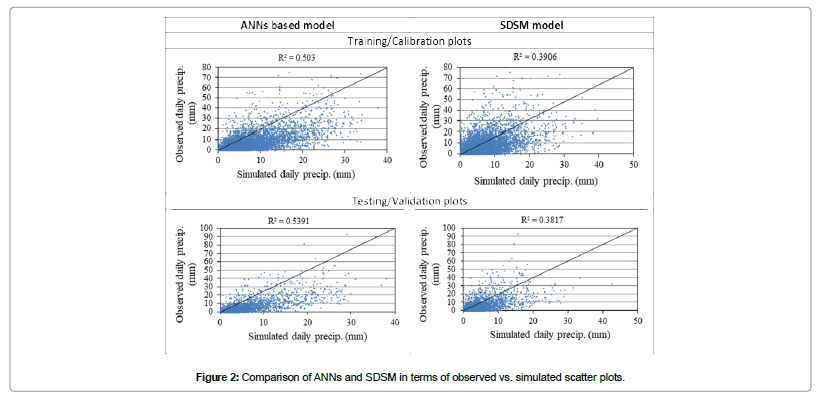
Model efficiency comparison of the ANNs based model and the SDSM model in terms of the values of RMSE and R2 is shown in Table 2 which reveals that the ANNs based model is more efficient than the SDSM model in both the calibration and the validation periods. It can be seen that the RMSE value obtained from ANNs based model is 5.070 as compared to 5.613 obtained for the SDSM for training/calibration. Likewise, R2 value for ANNs based model is 0.50 as compared to 0.39 for the SDSM for training/calibration. A similar trend has been observed for testing/validation. The higher level of the ANNs based model performance shows that it was able to detect, to a greater extent, the highly non-linear predictor-predictand relationship as compared to the SDSM model.
| Criteria | Simulation type | ANN | SDSM |
|---|---|---|---|
| RMSE | Training /Calibration | 5.070 | 5.613 |
| Testing /Validation | 5.180 | 6.033 | |
| R2 | Training /Calibration | 0.50 | 0.39 |
| Testing /Validation | 0.54 | 0.38 |
Table 2: Model efficiency comparison of the ANNs based model and the SDSM model in terms of the values of RMSE and R2.
Figure 2 presents the comparison of the ANNs based model with the SDSM model by showing daily observed vs. daily simulated scatter plots. This figure is a further confirmation and elaboration of what was revealed by the numeric values in Table 2, i.e., better performance of the ANNs based model over the SDSM model. In terms of the overall spread of obs-vs-sim scatter plots and spread around the diagonal line, the left column of Figure 2 (the ANNs based simulated data) has more agreement between the observed and simulated data than the right column.
Conclusion
The study presented in this paper aimed to explore the use of ANNs as a tool for downscaling daily precipitation for use in climate impact studies by comparing it with a widely used tool called the SDSM. To perform the modelling analysis required in this work, daily precipitation data of the Clutha watershed in New Zealand were used. Similar to previously published studies, the results of the SDSM modelling performed for the study presented [17] were set as a benchmark in order to analyse the performance of the ANNs based model fed with the same set of ten (10) predictor variables as were used in the final SDSM model [17]. Model comparison was performed by calculating and comparing the values of two widely used statistical parameters i.e., R2 and RMSE for the final SDSM and the ANNs based model and also by plotting the observed vs simulated scatter plots for both. Analysis of the results of this study reckons that the MLPANNs scheme can be used with confidence for developing a simple yet efficient predictors-predictand non-linear regression model that can be used for downscaling of daily precipitation for a watershed scale hyrological impact assessment study. Furthermore, by virtue of this study, the climate downscaling researchers are invited to broaden the exploration of similar artificial intelligence-soft computing techniques in the persuit of more efficient tools for climate downscaling (including precipitation) than the available lot [20,21].
Acknowledgments
The authors of this paper are thankful to the National Institute of Water and Atmospheric Research (NIWA), New Zealand for providing the daily precipitation data used in this study and the Higher Education Commission (HEC) of Pakistan for funding this research work.
References
- Maraun D, Wetterhall F, Ireson AM (2010) Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Reviews of Geophysics 48: 3.
- Snover AK, Mantua NJ, Littell JS (2013) Choosing and using climate-change scenarios for ecological-impact assessments and conservation decisions. Conserv Biol 27: 1147-1157.
- Xu CY (1999) From GCMs to river flow: A review of downscaling methods and hydrologic modelling approaches, Progress in Physical Geography 23: 229-249.
- Wilby RL, Charles SP, Zorita E (2004) Guidelines for use of climate scenarios developed from statistical downscaling methods, Supporting material of the Intergovernmental Panel on Climate Change. IPCC TGCIA. 27.
- Christensen JH, Carter TR, Rummukainen M (2007) Evaluating the performance and utility of regional climate models: The Prudence project. Climatic Change 81: 1-6.
- Douglas M, Martin W (2018) Statistical downscaling and bias correction for climate research. Cambridge University Press, USA.
- Hewitson BC, Daron J, Crane RG (2014) Interrogating empirical-statistical downscaling. Clim Chang 122: 539-554.
- Fistikoglu O, Okkan U (2010) Statistical downscaling of monthly precipitation using NCEP/NCAR reanalysis data fortahtali river basin in Turkey. Journal of Hydrologic Engineering 16: 157-164.
- Busuioc A, Tomozeiu R, Cacciamani C (2008) Statistical downscaling model based on canonical correlation analysis for winter extreme precipitation events in the Emilia-Romagna region. International Journal of Climatology 28: 449-464.
- Huth R (1999) Statistical downscaling in central Europe: Evaluation of methods and potential predictors. Climate Research 13: 91-101.
- Wilby RL, Dawson CW, Barrow EM (2002) SDSM-A decision support tool for the assessment of regional climate change impacts. Environmental Modelling and Software 17: 145-157.
- Mpelasoka FS, Mullan AB, Heerdegen RG (2001) New Zealand climate change information derived by multivariate statistical and artificial neural networks approaches. International Journal of Climatology 21: 1415-1433.
- Haylock MR, Cawley CG, Harpham C (2006) Downscaling heavy precipitation over the UK: A comparison of dynamical and statistical methods and their future scenarios. Int J Climatol 26: 1397-1415.
- Tripathi S, Srinivas VV, Nanjundiah RS (2006) Downscaling of precipitation for climate change scenarios: A support vector machine approach. Journal of Hydrology 330: 621-640.
- Tolika K, Maheras P, Vafiadis M (2007) Simulation of seasonal precipitation and raindays over Greece: A statistical downscaling technique based on artificial neural networks (ANNs). International Journal of Climatology 27: 861-881.
- Ahmed K, Shahid S, Haroon SB (2015) Multilayer perceptron neural network for downscaling rainfall in arid region: A case study of Baluchistan. J Earth Syst Sci 124: 1325.
- Hashmi MZ, Shamseldin AY, Melaville BW (2010) Comparison of SDSM and LARS-WG for simulation and downscaling of extreme precipitation events in a watershed. Stochastic Environmental Research and Risk Assessment 25: 1-10.
- Hashmi MZ, Shamseldin AY, Melville BW (2011) Statistical downscaling of watershed precipitation using Gene Expression Programming (GEP). Journal of Environmental Modelling and Software 26: 1639-1646.
- Fernando AK, Asaad YS, Robert JA (2011) Comparison of two data-driven approaches for daily river flow forecasting. 19th International Congress on Modelling and Simulation. p: 12-16.
- Schoof JT, Pryor SC (2001) Downscaling temperature and precipitation: A comparison of regression-based methods and artificial neural networks. International Journal of Climatology 21: 773-790.
- Shamseldin AY (2010) Artificial neural network model for river flow forecasting in a developing country. Journal of Hydroinformatics 12: 22-35.
Citation: Rahman Hashmi MZU, Shamseldin AY, Melville BW (2018) Comparison of MLP-ANN Scheme and SDSM as Tools for Providing Downscaled Precipitation for Impact Studies at Daily Time Scale. J Earth Sci Clim Change 9: 475. DOI: 10.4172/2157-7617.1000475
Copyright: © 2018 Rahman Hashmi MZU, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 4457
- [From(publication date): 0-2018 - Oct 19, 2025]
- Breakdown by view type
- HTML page views: 3519
- PDF downloads: 938