Comparative and Evaluate of Empirical Models for Estimation Global Solar Radiation in Al-Baha, KSA

Khalil SA; Aly HAS

doi:10.4172/2157-7617.1000492

Comparative and Evaluate of Empirical Models for Estimation Global Solar Radiation in Al-Baha, KSA

Khalil SA¹^* and Aly HAS²: ¹National Research Institute of Astronomy and Geophysics, Department of Solar and Space, Marsed Street, Helwan, Cairo, Egypt; ²Faculty of Women for Arts, Science and Education, Department of Physics, Ain Shams University, Cairo, Heliopolis, Egypt

^*Corresponding Author: Khalil SA, National Research Institute of Astronomy and Geophysics, Department of Solar and Space, Marsed Street, Helwan, Cairo, Egypt, Tel: +20225560645, Email: samynki@yahoo.com

Received: 18-Jul-2018 / Accepted Date: 10-Sep-2018 / Published Date: 15-Sep-2018 DOI: 10.4172/2157-7617.1000492

View PDF Download PDF

Keywords: Estimation solar radiation; Relative percentage error; Climate parameters; Statistical analysis; Clearness index and sunshine duration.

Introduction

The solar radiation is the most important energy resource to man and indeed it is essential factor for human life. The knowledge of solar radiation distribution at a particular geographical location is vital of solar energy devices; solar energy is the clean, abundant, renewable and sustainable energy resource from the sun which reaches the earth in form of light and heat [1,2]. The developing countries solar radiation data are not easily available for not being able to afford the data equipment and techniques involved [3-5]. The most for renewable and sustainable energy has increased research in in any given location. The solar radiation from the sun is fast becoming an alternative to other conventional sources of energy. The most of variable types of clean and energy basses, solar energy appears to be the most favored option because of its infinite and non-polluting nature [6-13]. The solar radiation is the most ancient source of energy; it is the basic element for almost all fossil and renewable types. Solar energy is freely available and could be easily harnessed to reduce our reliance on hydrocarbonbased energy by both, passive and active designs. Precise solar radiation estimation tools are critical in the design of solar systems [14-16].

The measurement of solar radiation is always a necessary basis for the design of any solar energy conversion device and for a feasibility study of the possible use of solar energy. The measured data are the best but cannot always be available [17-20]. Solar energy is mostly preferred due to being safe, clean, free, limitless and non-polluting. The total solar radiation data in a particular region are essential for energy applications because the photovoltaic panel is directly affected by solar radiation [21-25]. The knowledge of total solar radiation data is essential for the research and basses of the economic viability of systems that use solar energy [26]. The total solar radiation data important for solar energy use are in the form of diurnal variation, monthly mean daily values, frequency distribution of number of constant consecutive days in each certain month, with insulation below above a certain threshold and frequency distribution of monthly mean and annual mean values [27-30]. The measurements of the total solar radiation are very important to design the solar system, but it is not available in the few of countries, which depend on the prediction by using the meteorological parameters in any locality [31-35].

The developed models of correlation used in estimating total solar radiation in Locations of similar latitude, altitude and climatology, the accuracy of such models depends on the quality and quantity of the measured data used. Though less accurate, modeling is a better tool for the estimation of global solar radiation at places where measurements are not available [36-45]. The most common is the Angstrom-type one-parameter equation correlating the total solar radiation to the percentage of bright sunshine hours in a simple linear regression form [46-55].

The models of daily solar radiation con are dividing to models consider the effect of time [56-60], and models’ variation in weather conditions and distribution between hourly total solar radiations of all times which results in a normal distribution [61-68]. The total solar radiation of different local sites is usually globally required [69-75]. The solar radiation data obtained through direct measurements are not available for different places across the world. Thus, the various estimation procedures have been developed to evaluate total solar radiation [76-80].

The initial empirical correlation to estimate of the total solar radiation by Angstrom [81], the Angstrom correlation was adjusted by Prescott [82] and Page [83], and their modifications are being used widely to estimate total solar irradiance [84,85]. The several derivatives for predicting solar radiation over an entire country has been examined in many countries have also modified the correlation [86-100]. These different models exist that correlates with different meteorological [101-115]. Moreover, several empirical models have been used to estimate solar radiation; utilizing available geographical, climatological and meteorological parameters [116-134].

The accuracy of the developed model which is evaluated using statistical errors, a positive MBE value indicates the amount of overestimation in the predicted total solar energy and vice versa. On the other hand, RMSE provides information on the short-term performance of the model and is a measure of the variation of the predicted values around the measured data. RMSE also shows the efficiency of the developed model in predicting future individual values. A large positive RMSE implies a big deviation in the predicted value from the measured value [135-144].

The essence of this research is to development of models for estimating the total solar radiation for the selected location during the present time from 2005 to 2017 and compares the statistical results in the present work. The data in this study were obtained from the Meteorological and Environmental Protection Agency (MEPA) in KSA.

Selected Location

Al-Baha location is situated between (Lat. 200 01' N and Long. 410 28' E) and it is an important city in the south-western region of the Kingdom of Saudi Arabia between the Holy Makkah and Asir region (KSA) shown in Figure 1. The area of study is divided by huge and steep Rocky Mountains into two main sectors, a lowland coastal plain at the west, known as “Tehama”, and a mountainous area with an elevation of 1450 to 2400 m above sea level at the east, known as “Al-Sarat or Al-Sarah” which forms a part of Al-Sarawat Mountains. The selected location in summer is moderate and cold in winter with mean temperatures ranging between 12–23°C. With regard to general weather conditions, the temperature varies from a minimum of 3°C to a maximum of 30 °C and average of 18°C. The surface pressure changes from 750 to 769 mb with a mean value of 759 mb. The relative humidity varies between 5% and 96% with an average value of 51% [144,145].

Figure 1: Map of Al-Baha city is the location studied in the present study.

Factors Affecting the Solar Radiation

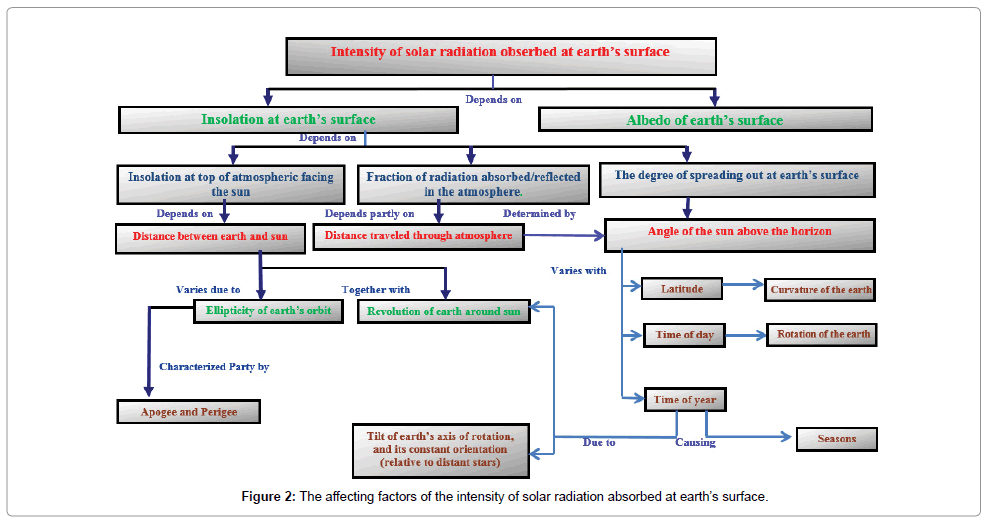
The factors affecting of the solar radiation absorbed at the Earth’s surface are consider fourth types; Firstly, the effect of the atmosphere in modifying the sun’s radiation before it arrives at earth surface is quite complex. When the sun rays get to within about 40 kilometers at earth surface some of the energy is absorbed in band of zone and some is absorbed and scattered by an upper dust layer which is periodically recharged volcanic eruption or galactic dust clouds. A considerable amount of energy is absorbed and scattered by dry air molecules, water vapor lying close to earth surface and seasonally varying lower layer dust. Secondly the distance between the Earth and Sun, the distance between the earth and sun at aphelion is equal to 152 million kilometer and at perihelia equal to 146.2 million kilometers. Third the incident angle of solar radiation, the earth receives maximum radiation when the radiation is incident at perpendicular to earth surface, when the incident angle of radiation increases the amount of radiation decrease. Also, the amount of radiation decreases with increase of atmosphere thickness which cross it. Fourth the length of day and rotation of earth, the earth rotated about the sun in 365.25 days and rotated by itself in 24 hours and the seasonal variation produce according to the inclined angle of earth axis rotation. The length of the days varies the amount of radiation received per days, then for long day the earth receives more radiation, more than short day these information’s are clear in Figure 2 [1].

earth-science-climatic-change-solar-radiation

Figure 2: The affecting factors of the intensity of solar radiation absorbed at earth’s surface.

Materials and Methods

The first correlation proposed for estimating the monthly average daily global radiation is based on the model of Angstrom [81]. The original Angstrom-Prescott type regression equation-related monthly average daily radiation to clear day radiation in a given location and average fraction of possible sunshine hours is given by the equation:

G/G_o = a+b (S/S_o) (1)

Where G is the monthly average daily global radiation on a horizontal surface (W/m²), G_o is the monthly average daily extraterrestrial radiation on a horizontal surface (W/m²), S the monthly average daily hours of bright sunshine, so is the monthly average day length, and “a” and “b” values are known as Angstrom constants and they are empirical.

Solar radiation incident outside the earth’s atmosphere is called extraterrestrial solar radiation. On average the extraterrestrial irradiance is 1367 W/m² (solar constant). The extraterrestrial radiation G_o is given as follows [143,146,147]:

G_o = (24/π) × I_SC × E_o × [cos φ cos δ sin ω+ (πω/180) sin φ sin δ] (2)

Where E_o is the correction factor of the Earth's orbit and ω is the sunrise/sunset hour angle given by:

E_o =1+0.033cos (2πdn/365), (3)

ω = cos^-1(-tan φ tan δ) (4)

And φ is latitude and the solar declination angle of the sun (δ) is the angle between a plane perpendicular to a line between the earth and the sun and the earth’s axis, which given in degrees according to Spencer [148] as:

δ = (0.006918-0.399912 cosΓ+0.070257 sinΓ-0.006758 cos2Γ+0.000907 sin2Γ-0.002697 cos3Γ+0.00148 sin 3Γ) (180/π) (5)

Where Γ is the day angle in radiance, it is represented by:

Γ = 2(d_n-1)/365 (6)

Where d_n is day of the year.

Therefore, the monthly mean of daily global radiation G was normalized by dividing with monthly mean of daily extraterrestrial radiation G_o. We can define clearness index (K_T) as the ratio of the observed/measured horizontal terrestrial solar radiation G, to the calculated/predicted horizontal/extraterrestrial solar radiation (G_o). Clearness index (K_T) gives the percentage deflection by the sky of the incoming global solar radiation and therefore indicates both level of availability of solar radiation and changes in atmospheric conditions in a given locality.

K_T = G/G_o (7)

The commonly used solar energy models developed in the past are based on linear and nonlinear models [109]. These models give a correlation between solar energy on a horizontal surface and some meteorological variables such as; shine hour’s s, ambient temperature T, cloud cover c_w, relative humidity R_h, and maximum T_max. and T_min. ambient temperatures. The linear models use simple linear function while the nonlinear models are polynomial function of the third or fourth degree [5,148].

Solar researchers have developed many empirical correlations which determine the relation between solar radiation and various meteorological parameters. As the availability of meteorological parameters, which are used as the input of radiation models is the most important key and output of radiation models (i.e., solar irradiance and solar irradiation). Among the models, some of them are based on ratio of monthly average daily global radiation to the extraterrestrial radiation (G/G_o), non-linear and some are based on empirical coefficients ‘a’ and ‘b’. Proposed models for the present research are listed in Table 1 [1].

Model No.	Regression equation	Model type	Model S_ource
1	G/G_o = a+b (S/S_o) (8)	Linear –Single Parameter	Angstrom, (1924) and Prescott (1940)
2	G/G_o = a+b log (S/S_o) (9)	Logarithmic	Ampratwum and Dorvlo (1999)
3	G/G_o = a+b exp (S/S_o) (10)	Exponential	Almorox et al. (2005)
4	G/G_o = a+b (RH) (11)	Linear –Single Parameter	Agbo et al. (2013)
5	G/G_o = a+b (ΔT/S_o) (12)	Linear – Double Parameter	Garica (1994)
6	G/G_o = a+b (q) (13)	Linear –Single Parameter	Okonkwo and Nwokoye (2014)
7	G/G_o = a+b (q) + c (q)² (14)	Quadratic	Okonkwo and Nwokoye (2014)
8	G/G_o = a+b (S/S_o) + c (S/S_o)² (15)	Quadratic	Akinoglu and Ecevit (1990)
9	G/G_o = a+b (S/S_o) + c R_H (16)	Multiple - Parameter	Swarthman-Oguniade (1964)
10	G/G_o = a+b (S/S_o) + c (ΔT/S) (17)	Multiple Meteo. Parameter	Olomiyesan and Oyedum (2016)
11	G/G_o = a+b (S/S_o) (18)	Linear – Single Parameter	Louche et al. (1991)
12	G/G_o = a+b (S/S_o) (19)	Linear – Single Parameter	Page (1964)
13	G/G_o = a+b (S/S_o) + c (S/S_o)² (20)	Quadratic	Bahel (1987)
14	G/G_o = a+b (S/S_o) + c (S/S_o)² (21)	Quadratic	Zabara (1986)
15	G/G_o = a[1-e(-bΔTc)] (22)	Exponential	Bristow and Campbell (1984)

Table 1: Proposed models for the present work.

Modeling Techniques

There are numerous works in literature which deal with the assessment and comparison of monthly mean daily solar radiation estimation models. The relative ability of the different models to predict the solar radiation on horizontal and tilted surfaces was tested. The performance of the individual models was determined by utilizing statistical methods. There are numerous works in literature which deal with the assessment and comparison of daily solar radiation estimation models. The most popular statistical parameters are the MBE (mean bias error) and the RMSE (root mean square error). In this study, to evaluate the accuracy of the estimated data, from the models described above, the following statistical estimators were used, MBE, RMSE, MPE (mean percentage error) and the correlation coefficient (R²), to test the linear relationship between predicted and measured values. For higher modeling accuracy, these estimators should be closer to zero, and the correlation coefficient, (R²), should approach to 1. However, these estimated errors provide reasonable criteria to compare models but do not objectively indicate whether the estimates from a model are statistically significant. The t-Test statistic allows models to be compared and at the same time it indicates whether or not a model’s estimate is statistically significant at a particular confidence level. So, the t-Test was carried out on the models to determine the statistical significance of the predicted values [84].

Mean Bias Error (MBE)

To evaluate the accuracy of the prediction data from the models described above, this test provides information on the long-term performance of a model. A low MBE value is desired. A negative value gives the average amount of underestimation in the calculated value. So, one drawback of MBE is that overestimation of an individual observation may cancel underestimation in a separate observation. We can be obtained the values of MBE as follow:

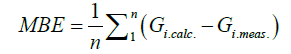equation (23)

And the equation of mean percentage error MPE% is expressed by:

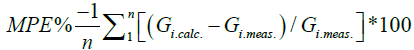equation (24)

The subscript i refer to the ith value of the daily solar irradiation; n is the number of the daily solar irradiation data. The subscripts “calc.” and “meas.” refer to the calculated and measured daily solar irradiation values, respectively. A percentage error between -10% and +10% is considered acceptable [143].

Root Mean Square Error (RMSE)

The value of RMSE is always positive, representing zero in the ideal case. The normalized RMSE gives information on the short-term performance of the correlations by allowing a term-by-term comparison of the actual deviation between the predicted and measured values. The smaller the value, the better the model’s performance is, and the equation of RMSE as follows [144].

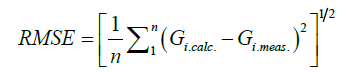equation (25)

The t-Test statistic (t)

The tests for mean values, the random variable t with n-1 degrees of freedom may be written here as follows [145].

t = [(n-1) (MBE)²/ (RMSE)² – (MBE)² ]^1/2 (26)

The smaller values of t-statistic the better the performance of modeling.

The correlation coefficient (R²)

In statistics literature, it is the proportion of variability in a data set that is accounted for by a statistical model, where the variability is measured quantitatively as the sum of square deviations. Most often it is defined notationally as:

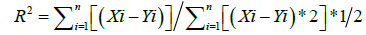equation (27)

This can also be expressed as:

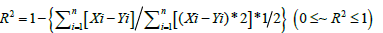equation (28)

Herein, Xi and Yi are the measurements and model estimates, respectively. A high value of R² is desirable as this shows a lower unexplained variation. R² is a statistic that gives some information about the goodness-of-fit of a model. In regression, the R² coefficient of determination is a statistical measure of how well the regression line approximates the real data points. An R² of 1.0 indicates that the regression line perfectly fits the data, which is never valid in any solar radiation estimation model.

The relative percentage error (e) of the estimated values of the global solar radiation at each site may be calculated from the following equation:

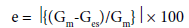equation (29)

Results and Discussion

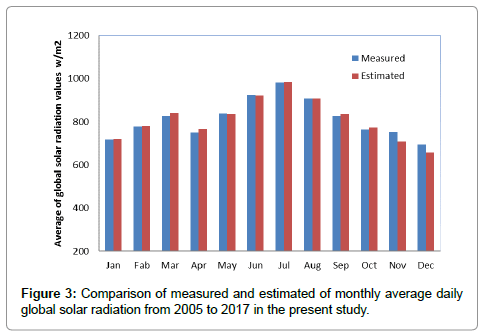
The comparison between measured and estimated values of monthly average daily global solar radiation during the period time from 2005 to 2017 in the present study is illustrated in Figure 3. We noticed that a good agreement between measured and estimated values of the global solar radiation for the whole months in the present study. As can be seen from this figure a small deviation between measured and estimated values of global solar radiation during the period time in the current study. The deviation between measured and estimated values does not exceed 6%. It is also noticeable from this figure that the maximum values of global solar radiation in the summer months. While, the lowest values ranging between the values of the global solar radiation in the winter and autumn months and the differences between them are almost equal. We also conclude that the global solar radiation values in the spring months lie between the highest value of summer and the lowest values in the winter and autumn months. The estimated values of the global solar radiation are nearly coinciding with the measured values. It is clear that, the accuracy of model that used in the present work is almost coinciding with measured for average monthly variation in the selected location. It is clear from the previous results that the model that used in the study gives good results compared to the measured results of global solar radiation during the period time in the present research.

earth-science-climatic-change-global-solar

Figure 3: Comparison of measured and estimated of monthly average daily global solar radiation from 2005 to 2017 in the present study.

The monthly average values of the extraterrestrial solar radiation (G_o W/m²), measured (G_mes. W/m²), estimated global solar radiation (G_est. W/m²), and the climate parameters; the fraction of sunshine hours (S/S_o), clearness index (kT = G_mes./G_o), relative humidity (RH), the ratio between min. and max. temperature (θ), the differences between max. and min. temperature (ΔT) and the ratio of change in temperature to day length (ΔT/S_o) in the present research during the period time from 2005 to 2017 are listed in Table 2. From this table we notice that the ratio between the measured and estimated global solar radiation with extraterrestrial solar radiation is varies 68-76% and 68-75% respectively. Therefore, the differences between maximum and minimum are varying from 24% to 32%. Moreover, the average differences between measured and estimated solar radiation to the extraterrestrial solar radiation in the present work during the period time not exceed 8%. Also, we noticed that the change between measured and estimated values of solar radiation does not exceed 3%. Also, we noticed that from this table the change between the climate parameters; (KT, RH, θ and ΔT/S_o) for all months during the period time in the present study are small variables.

Month	G_o	G_mes.	G_est.	S/S_o	G_mes./G_o=KT	R_H %	q	ΔT	ΔT/S_o
Jan	6652	4637	4532	0.875	0.697	81	0.467	8	0.728
Feb	7862	5578	5489	0.911	0.709	85	0.470	9	0.793
Mar	9542	6485	6534	0.842	0.680	88	0.450	10	0.858
Apr	10321	7631	7712	0.815	0.739	71	0.455	11	0.925
May	10945	7826	7698	0.809	0.715	72	0.462	14	1.21
Jun.	11238	8564	8435	0.861	0.762	82	0.464	15	1.278
Jul	10756	7782	7647	0.922	0.724	75	0.483	16	1.342
Aug	10412	7345	7512	0.913	0.705	72	0.429	15	1.213
Sep	9756	6689	6746	0.882	0.686	77	0.407	14	1.099
Oct	8923	6348	6489	0.842	0.711	81	0.434	13	1.101
Nov	7537	5537	5637	0.869	0.735	86	0.474	11	0.942
Dec	6496	4489	4529	0.831	0.691	84	0.500	9	0.789

Table 2: Mean value of input climate parameters for selected site in the present work.

The monthly relative percentage error (e) between the estimated (by each model) and measured values of global solar radiation of the year in the present work during the period time from 2005 to 2017 is summarizing in Table 3. The required variables were substituted into each of the aforementioned models to estimate global solar radiation. The performance of each model in predicting the measured solar radiation was then measured using the above statistics. Then, we first consider the predictability of each model during each month of the year using the relative percentage error. The overall performance using the rest of the statistical indicators will be second step to selecting the best model. A relative percentage error between -10 to 10% is considered acceptable for reasonably predicting global solar radiation data for many applications. The relative percentage error varies by model and by month. Therefore, we briefly discuss the main feature and issues in the performance of the models. Table 3 includes fifteen models, which are used to estimate global solar radiation in the current study during the period time from 2005 to 2017. We can divide these models into five different categories.

Model	Eq. No.	Month
Model	Eq. No.	Jan.	Feb.	Mar.	Apr.	May	Jun.	Jul.	Aug.	Sep.	Oct.	Nov.	Dec.
Angstrom	8	11.25	6.52	4.21	8.37	15.34	7.54	3.87	-0.91	-0.64	-4.51	6.27	1.87
Ampratwum	9	15.67	4.35	-3.75	7.34	12.37	6.48	-3.74	-2.89	1.56	6.21	-4.68	1.36
Almorox	10	-22.11	15.37	4.35	5.32	4.65	2.89	-3.45	-0.95	2.65	-1.45	1.34	-4.52
Agbo	11	9.23	-3.65	2.89	1.65	-7.35	-4.12	2.38	1.89	-0.45	-0.18	4.56	2.75
Garica	12	18.56	-2.56	4.65	2.89	-3.45	-7.25	-4.89	5.65	7.32	4.23	1.57	-6.27
Okonkwo)	13	5.32	7.25	-25.22	15.32	-5.36	-3.57	-2.87	1.68	2.54	7.32	6.45	9.28
Nwokoye	14	16.25	-15.68	-9.45	14.32	17.32	11.78	5.64	19.45	17.32	-5.45	13.45	1.98
Akinoglu	15	13.56	-15.21	-8.34	13.78	12.78	11.54	-6.45	4.65	13.78	12.45	11.98	11.35
Swarthman	16	-0.65	1.35	3.87	2.35	1.78	11.45	8.35	4.35	-3.12	6.58	9.45	10.65
Olomiyesan	17	3.45	6.89	-3.41	9.56	16.32	9.45	4.65	3.26	7.32	12.54	2.56	1.54
Louche et	18	15.32	2.69	11.54	-3.56	-6.89	3.78	4.35	4.35	2.45	1.67	11.25	8.32
Page	19	5.32	-6.45	9.48	2.45	11.78	9.32	8.45	10.56	7.35	-3.45	-8.32	-6.54
Bahel	20	11.35	16.48	12.35	24.11	9.45	-13.15	2.34	6.45	18.45	10.35	7.35	16.34
Zabara	21	16.45	13.15	-13.45	2.78	1.38	-16.32	8.32	5.32	24.23	14.32	22.87	11.32
Bristow	22	11.32	9.32	5.46	11.89	2.87	4.45	-3.45	-2.41	9.45	13.12	15.32	-3.76

Table 3: Monthly relative percentage error (e) of the models in the present study.

The first category, the (e) value ranges between 18.56 and -0.18%. All the models in these categories performed well in the months of February, April, July, August, September and October. In October month the models demonstrated the lowest (e) attained by equation (11). The highest (e) values were observed in January month, when equation (12) had the highest values. As regarding, the second category as performed in equation (9). The lowest (e) value is observed in August month. While the highest value is occurred in January month. In addition to the (e) values in March, July and November months consider small values. The third category exhibited significant differences in performance. Equations (10) and (22) demonstrated extremely variable of (e) in all months, the (e) values range from 15.37 to -0.95% and 15.32 to -2.41 respectively. The lowest value of (e) in equations (10) and (22) are observed in July, August and October months. The fourth category there were major discrepancies and the best and worst performing models were in this category. Equation (14) demonstrated the highest value of (e) of all models considered in this study. The highest (e) was 19.45% in the month of August in equation (14). Equations (14), (15), (20) and (21) reported values of (e) less than 10% through March, July and August months. The last category the (e) value range from 16.32 to -0.65% by equation (16) and (17). The lowest value of (e) is occurring in January month for equation (16) and the highest values observed in equation (17) during May month. We notice from the above discussion that the models are performed differently for different months. Some models performed well in some months, while others performed poorly, and vice versa. In addition, some models demonstrated reasonable predictability, while others produced unreliable estimations.

Summarized values of statistical parameters and regression coefficient in the present study during the period time from 2005 to 2017 is listed in Table 4. From this table we select the model with the most accurate performance in estimating global solar radiation in the current study by assessing overall performances using the overall MBE, RMSE, MPE, R² and t-test. Selected the best model is to reduce the number of equations by allowing MPE values between -10 and 10% to be an acceptable range. Using this criterion, we excluded eleven models, leaving five. Three of these five were from first category Eq (12), (20) and new model, one from first category eq (12) and the last one from fourth category eq (20). Among these models, three of them exhibited on MPE and RMSE less than 2%, and other two models less than 8%. While value of R² for three models Eq 12, 20 and new model are 0.963, 0.959 and 0.972 respectively. The lowest values of t-test observed in models no. (12, 20, and new model), this means that, these models consider the best for using to estimate global solar radiation. Finally, the models of Graica eq 12, Bahel eq 20 and new model was the most suitable relation for estimating the global solar radiation for Al-Baha site, KSA.

Model No.	Model Type	Statistical parameters					Regression constants
Model No.	Model Type	MBE	MPE (%)	RMSE	R²	t-statistical	a	b	c
1	Linear –Single Parameter	1.25	7.85	2.56	0.896	4.12	2.459	-3.456	-
2	Logarithmic	3.26	5.69	3.56	0.912	6.23	1.358	-1.325	-
3	Exponential	2.89	11.23	5.63	0.853	8.12	3.589	-0.358	-
4	Linear –Single Parameter	0.89	15.65	4.89	0.867	3.12	1.345	-2.358	-
5	Linear – Double Parameter	0.67	1.63	1.32	0.963	1.67	4.325	-1.357	-
6	Linear –Single Parameter	3.78	19.45	5.62	0.9123	5.34	5.321	-3.356	-
7	Quadratic	2.67	15.27	7.89	0.885	4.76	1.658	-4.235	-3.248
8	Quadratic	1.98	17.89	9.52	0.845	5.89	2.965	2.315	1.895
9	Multiple - Parameter	-2.65	13.45	5.45	0.796	7.32	0.658	-2.354	-3.126
10	Multiple Meteo. Parameter	-3.56	15.12	4.23	0.832	4.89	0.123	-1.985	2.356
11	Linear – Single Parameter	2.98	18.32	2.13	0.953	6.89	3.269	-3.245	-
12	Linear – Single Parameter	3.56	11.45	5.23	0.847	5.45	1.638	-1.358	-
13	Quadratic	4.89	1.89	1.32	0.959	1.45	0.689	-7.345	-5.648
14	Quadratic	-1.89	12.45	5.32	0.882	4.78	0.752	-0.625	-7.234
15	Exponential	-1.65	16.34	2.38	0.872	6.78	4.368	-0.795	2.358
New Model	Linear	0.84	1.23	1.61	0.972	1.23	0.175	0.265	-1.84

Table 4: Statistical parameters and regression constants for different models in selected site.

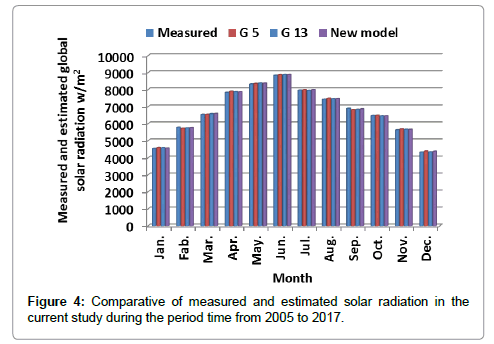
The comparative study of measured and estimated of global solar radiation for Al-Baha location in the period time from 2005 to 2017 is illustrated in Table 5. From this table it has been noticed that the estimated global solar radiation by using all sixteen models are in close agreement with the measured value of global solar radiation in the present study from 2005 to 2017. Also, it is observed that the values of the global solar radiation estimated by models (G5, G13 and new model) are good with measured data. The values of global solar radiation in other models are highly overestimated or underestimated. The estimated values of global solar radiation by modeling (G5, G13 and new model) and measured data are illustrated in Figure 4. From this figure we observed that good agreement between estimated and measured global solar radiation. The deviation between measured and estimated values is not exceeding 1%.

earth-science-climatic-change-estimated-solar

Figure 4: Comparative of measured and estimated solar radiation in the current study during the period time from 2005 to 2017.

Month	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
G_mes	4539	5786	6538	7826	8325	8832	7963	7425	6895	6475	5632	4326
G₁	4426	5632	6689	7936	8521	8736	7826	7536	6723	6528	5746	4438
G₂	4638	5842	6672	7789	8435	8935	7763	7625	6923	6389	5576	4536
G₃	4721	5673	6645	7921	8457	8934	8318	7562	6945	6548	5763	4298
G₄	4638	5596	6476	7725	8463	8739	7824	7347	6725	6378	5526	4472
G₅	4595	5723	6575	7895	8352	8869	7896	7486	6825	6488	5679	4385
G₆	4478	5637	6645	7735	8496	7683	7924	7612	6735	6548	5538	4438
G₇	4638	5589	6725	7695	8523	8925	7786	7568	6698	6389	5473	4538
G₈	4732	5627	6698	7915	8476	8745	7834	7645	6734	6528	5723	4493
G₉	4692	5693	6723	7735	8236	8695	7728	7586	6725	6632	5589	4527
G₁₀	4465	5711	6637	7697	8296	8738	7865	7637	6935	6472	5422	4621
G₁₁	4595	5811	6632	7825	8398	8875	8105	7496	6827	6387	5697	4386
G₁₂	4678	5827	6686	7997	8476	8795	7892	7575	6934	6527	5786	4473
G₁₃	4583	5741	6571	7866	8376	8872	7943	7454	6838	6447	5661	4337
G₁₄	7588	5673	6489	7758	8421	8932	7825	7526	6758	6345	5542	4473
G₁₅	4568	5548	6623	7821	8397	8915	7798	7612	6697	6289	489	4523
New Model	4562	5762	6582	7855	8373	8874	7993	7465	6862	6449	5658	4374

Table 5: Monthly mean measured and estimated values of global solar radiation (W/m²) in the present work during the period time from 2005 to 2017.

Conclusion

The objective of this study is to evaluate various models for the estimation of the monthly average daily global radiation on a horizontal surface from bright sunshine hours, relative humidity and temperatures ratio for Al-Baha, KSA. The collected models were comparative on the basis of the statistical error tests such as mean bias error (MBE), the mean percentage error (MPE), root mean square error (RMSE), correlation coefficient (R²) and t-test in the present study. Good agreement between measured and estimated values of the global solar radiation for the whole months in the present study. The maximum values of global solar radiation in the summer months. While, the lowest values ranging between the values of the global solar radiation in the winter and autumn months and the differences between them are almost equal. The estimated values of the global solar radiation are nearly coinciding with the measured values. The deviation between measured and estimated values does not exceed 6%. The ratio between the measured and estimated global solar radiation with extraterrestrial solar radiation is varies 68-76% and 68-75% respectively. The differences between maximum and minimum are varying from 24% to 32%. Moreover, the average differences between measured and estimated solar radiation to the extraterrestrial solar radiation in the present work during the period time not exceed 8%. Also, we noticed that the change between measured and estimated values of solar radiation does not exceed 3%.

The relative percentage error between -10 to 10% is considered acceptable for reasonably predicting global solar radiation data for many applications. The relative percentage error varies by model and by month. The first category, the (e) value ranges between 18.56 and -0.18%. All the models in these categories performed well in the months of February, April, July, August, September and October. The second category as performed in equation (9). The lowest (e) value is observed in August month. While the highest value is occurred in January month. The third category exhibited significant differences in performance. Equations (10) and (22) demonstrated extremely variable of (e) in all months, the (e) values range from 15.37 to -0.95% and 15.32 to -2.41% respectively. The fourth category there were major discrepancies and the best and worst performing models were in this category. The last category the (e) value range from 16.32 to -0.65% by equation (16) and (17). The models are performed differently for different months. Some models performed well in some months, while others performed poorly, and vice versa. In addition, some models demonstrated reasonable predictability, while others produced unreliable estimations.

The regression coefficients of some collected solar models have been generally presented to estimate the global solar radiation with high accuracy in a given site. The statistical results appear that, models of Graica eq 12, Bahel eq 20 and new model was the most suitable relation for estimating the global solar radiation for Al-Baha site, KSA. The estimated global solar radiation by using all sixteen models is in close agreement with the measured value of global solar radiation in the present study from 2005 to 2017. The values of the global solar radiation estimated by models (G5, G13 and new model) are good with measured data. The values of global solar radiation in other models are highly overestimated or underestimated. Good agreement between estimated and measured global solar radiation. The deviation between measured and estimated values is not exceeding 1%. Finally, according to the climate parameters and statistical results, we observed a new simple linear model:

[(G/G_o) = 0.175 + 0.265 (S/S_o) – 1.84(S/S_o)₂]

Based on modified Angstrom model is recommended to estimate monthly average daily global solar radiation Al-Baha site, KSA, and in other areas with similar climatic conditions where the radiation data is missing or unavailable. The current research will help to advance the state of knowledge of global solar radiation to the point where it has applications.

References

Jamilu M, Abdullahi GM, Yusif AY, Mika’il AA (2018)Global solar radiation models: A review.Journal of Photonic Materials and Technology 4: 26-32.
Namrata K, Sharma SP (2012) Comparison of estimated daily global solar radiation using different empirical models. 2: 132-137.
Teke A, Yıldırım HB, Çelik Ö (2015) Evaluation and performance comparison of different models for the estimation of solar radiation. Renewable and Sustainable Energy Reviews 50: 1097-1107.
Nik WBW, Ibrahim MZ, Samo KB, Muzathik AM (2012) Monthly mean hourly global radiation estimation. J Solar Energy 86: 379-387.
Sulaiman MY, Umar AB (2017) A comparative analysis of empirical models for the estimations of monthly mean daily global solar radiation using different climate parameters in Sokoto, Nigeria. International Journal of Marine, Atmospheric and Earth Sciences 5: 1-19.
Okonkwo GN, Nwokoye AOC (2014) Estimating global solar radiation from temperature data in minna location. European Scientific J 10: 15.
Bolaji BO (2005) Development and performance evaluation of a Box- Type Absorber Solar Air Collector for Crop Drying. J Food Technology 3: 595-600.
Chiemeka IU (2008) Estimation of solar radiation at Uturu, Nigeria. Int J Physical Science 3: 126-130.
Duffie JA, Beckman WA (1991) Solar engineering of thermal processes. (2nd edn) John Wiley and Sons press, New York, USA. p: 944.
El-Sebaii AA, Trabea AA (2005) Estimation of global solar radiation on horizontal surfaces over Egypt. Egypt J Solids 28: 163-166.
Falayi EO, Rabiu AB (2008) Prediction of clearness index for some nigerian stations using temperature data. J Sci & Tech 28: 94-101.
Igbal M (1983) An introduction to solar radiation.(1st edn) Academy Press, New York,USA. p: 408.
Iheonu EE (2001) Model for the prediction of average monthly global solar radiation on a horizontal surface for some locations in the tropics using temperature data. Nig J Solar Energy 9: 12-15.
Liu BYH, Jordan RC (1960) The interrelationship and characteristic distribution of direct, diffuse and total solar radiation. J Solar Energy 4: 1-19.
Pereira MC, Rabl A (1979) The average distribution of solar radiation-correlations between diffuse and hemispherical and between daily and hourly insolation values. J Solar Energy 22: 155-164.
Gueymard C (1986) Mean daily averages of beam radiation received by tilted surfaces as affected by the atmosphere. J Solar Energy 37: 261-267.
Garg HP, Garg SN (1987) Improved correlation of daily and hourly diffuse radiation with global radiation for Indian stations. J Solar and Wind Technology 4: 113-126.
Gueymard C (2000) Prediction and performance assessment of mean hourly global radiation. J Solar Energy 68: 285-303.
Ahmad MJ, Tiwari GN (2008) Study of models for predicting the mean hourly global radiation from daily summations. Open Environmental Sciences J 10: 6-14.
Jain PC (1984) Comparison of techniques for the estimation of daily global irradiation and a new technique for the estimation of hourly global irradiation. Solar Wind Technology p: 123-134.
Jain PC (1988) Estimation of monthly average hourly global and diffuse irradiation. Solar & Wind Technology p: 7-14.
Baig A, Akhter P, Mufti A (1991) A novel approaches to estimate the clear day global radiation. Renewable Energy p: 119-123
Shazly SME (1996) Estimation of hourly and daily global solar radiation at clear days using an approach based on modified version of Gaussian distribution. Adv Atmos Sci 13: 349-358.
Newell TA (1983) Simple models for hourly to daily radiation ratio correlations. J Solar Energy 31: 339-342.
Yao W, Li Z, Xiu T, Lu Y, Li X (2015) New decomposition models to estimate hourly global solar radiation from the daily value. J Solar Energy 120: 87-99.
Oluseyi OA, Fagbenle RO, James K, Joshua OO, Omotosho OA (2010) Wind energy potential for power generation of a local site in Gusau, Nigeria. Int J Energy Clean Environ 11: 99-116.
Ajayi OO, Fagbenle RO, Katende J (2011) Assessment of wind power potential and wind electricity generation using WECS of two sites in South West, Nigeria. Int J Energy Sci 1: 78-92.
Ajayi OO, Fagbenle RO, Katende J (2011) Wind profile characteristics and econometric analysis of wind power generation of a site in Sokoto State, Nigeria. Energy Sci Technol 1: 54-66.
Chegaar M, Chibani A (2011) A simple method for computing global solar radiation. Rev Energ Ren Chemss 1: 54-66.
Chineke TC (2008) Equations for estimating global solar radiation in data sparse regions. Renewable Energy 33: 827-831.
Fadare DA (2009) Modelling of solar energy potential in Nigeria using artificial neural network model. Appl Energy 86: 1410-1422.
Islam MD, Kubo I, Ohadi M, Alili AA (2009) Measurement of solar energy radiation in Abu Dhabi, UAE. Appl Energy 86: 511-515.
Jin Z, Wu Y, Gang Y (2005) General formula for estimation of monthly average daily global solar radiation in China. Energy Convers Manage 46: 257-268.
Akpabio LE, Etuk E (2003) Relationship between global solar radiation and sunshine duration for Onne, Nigeria. Turk J Phys 27: 161-167.
Robaa SM (2003) On the estimation of global and diffuse solar radiation over Egypt, Mausam. 54: 17-35.
Robaa SM (2009) Validation of the existing models for estimating global solar radiation over Egypt. Energy Convers Manage 50: 184-193.
El-Metwally M (2005) Sunshine and global solar radiation estimation at different sites in Egypt. J Atmos Solar Terr Phys 67: 1331-1342.
Massaquoi JGM (1988) Global solar radiation in Sierra Leon (West Africa). Solar Wind Technol 5: 281-283.
Kamal S (2006) Correlation of global solar radiation with common geographical and meteorological parameters for Damascus province, Syria. Energy Convers Manage 47: 331-345.
Lof GOG, Duffie JA, Smith CO (1966) World distribution of solar radiation. Sol Energy 10: 27-37.
Rietveld MR (1978) A new method for estimating the regression coefficients in the formula relating solar radiation to sunshine. Agric Meteorol 19: 243-252.
Soler A (1990) Statistical comparison for 77 European stations of sunshine based models. J Sol Energy 45: 365-370.
Turton SM (1987) The relationship between total irradiation and sunshine duration in the humid tropics. J Sol Energy 38: 353-354.
Haluoani N, Nguyen CT, Vo-Ngoc D (1993) Calculation of monthly average global solar radiation on horizontal surfaces using daily hours of bright sunshine. Sol Energy 50: 247-258.
Ma CCY, Igbal M (1984) Statistical comparison of solar radiation correlations, monthly average global and diffuse radiation on horizontal surfaces. J Sol Energy 33: 143-148.
Hutchinson MF, Booth TH, McMahon JP, Nix HA (1984) Estimating monthly mean value of daily total solar radiation for Australia. J Sol Energy 32: 277-290.
Samuel TDMA (1991) Estimation of global radiation for Sri Lanka. J Sol Energy 47: 333-337.
Hawas MM, Muneer T (1983) Correlation between global radiation and sunshine data for India. Sol Energy 30: 289-290.
Raja IA, Twidell JW (1989) Distribution of global insulation over Pakistan. J Sol Energy 43: 335-357.
Ledanois JM, Prieto AA (1988) New solar map of Venezuela. Sol Energy 41: 115-26.
Alaruri SD, Amer MF (1993) Empirical regression models for weather data measured in Kuwait during the years 1985, 1986 and 1987. Sol Energy 50: 229-233
Ahmad I, Al-Hamadani N, Ibrahim K (1983) Solar radiation maps for Iraq. Sol Energy 31: 29-44.
Tiris M, Tiris C, Ture E (1996) Correlations of monthly average daily global, diffuse and beam radiations with hours of bright sunshine in Gebze, Turkey. Energy Converse Manage 37: 1417-1421.
Togrul IT, Togrul H, Evin D (2000) Estimation of global solar radiation under clear sky radiation in Turkey. Renewable Energy 21: 271-287.
Leung CT (1980) The fluctuation of solar irradiance in Hong Kong, Sol Energy 25: 485-94.
Newland FJ (1989) A study of solar radiation models for the coastal region of South China. Sol Energy 43: 227-235.
Excell RHB (1976) The solar radiation climate of Thailand. Sol Energy 18: 249-354
Chuah Donald GS, Lee SL (1981) Solar radiation estimates in Malaysia. Sol Energy 26: 33-40.
Goh TN (1979) Statistical study of solar radiation information in an equatorial region (Singapore). Sol Energy 22: 105-111.
Nguyen BT, Pryor TL (1997) the relationship between global solar radiation and sunshine duration in Vietnam. Renewable Energy 11: 47-60.
Lin W, Lu E (1998) Correlations between monthly average global solar radiation on horizontal surfaces and relative duration of sunshine in Yunnan province, China. Renewable Energy 13: 355-362.
Kamel MA, Shalaby SA, Mostafa SS (1993) solar radiation over Egypt: comparison of predicted and measured meteorological data. Sol Energy 50: 463-467.
Tadros MTY (2000) Uses of sunshine duration to estimate the global solar radiation over eight meteorological stations in Egypt. Renewable Energy 21: 231-246.
Ezekwe CI, Ezeilo Clifford CO (1981) Measured solar radiation in a Nigerian environment compared with predicted data. Sol Energy 26: 181-186.
Khogali A (1983) Solar radiation over Sudan-comparison of measured and predicted data. Sol Energy 31: 41-53.
Gopinathan KK (1992) Estimation of hourly global and diffuse solar radiation from hourly sunshine duration. Sol Energy 48: 3-5.
Singh OP, Srivastava SK, Gaur A (1996) Empirical relationship to estimate global radiation from hours of sunshine. Energy Convers Manage 37: 501-504.
Sezai I, Tasdemiroglu E (1995) Evaluation of the meteorological data in northern Cyprus. Energy Convers Manage 36: 953-961.
Reddy SJ (1971) Sn empirical method for estimation of the total solar radiation. Sol Energy, p.13.
Ododo JC, Usman A (1996) Correlation of total solar radiation with common meteorological parameters for Yola and Calabar, Nigeria. Energy Convers Manage 37: 521-530.
Sabbagh JA, Sayigh AA, El-Salam MA (1977) Estimation of the total solar radiation from meteorological data. Sol Energy 19: 307-311.
Togrul IT, Onat E (1999) A study for estimating solar radiation in Elazig using geographical and meteorological data. Energy Convers Manage 40: 1577-1584.
Trabea AA, Shaltout MAM (2000) Correlation of global solar radiation with meteorological parameters over Egypt. Renewable Energy 21: 297-308.
Ertekin C, Yaldiz O (1999) Estimation of monthly average daily global radiation on horizontal surface for Antalya, Turkey. Renewable Energy 17: 95-102.
Akpabio LE, Etuk SE (2003) Relationship between global solar radiation and sunshine duration for Onne, Nigeria. Turk J Phys 27: 161-167.
Ododo JC (1994) New models for the prediction of solar radiation in Nigeria, Paper presented at the 2nd OAU/STRC Conference on New. Renewable and Solar Energies at Bamako Mali. pp: 16-20.
Sanusi YA (2004) Ranking of the performance of some climatological parameters in estimation of solar radiation in the Minna environment, Central Nigeria. Nig J Ren Energy 12: 27-37.
Togrul IT (2009) Estimation of Solar Radiation from Angstroms Coefficients by Using Geographical And Meteorological Data in Bishkek, Kyrgyzstan J. Therm. Sc. Tech 29: 99-108.
Angstrom A (1924) Solar and terrestrial radiation. Quart J Roy Meteor Soc, pp: 50-121.
Prescott JA (1940) Evaporation from a water surface in relation to solar radiation. Trans R Soc. South Aust, pp: 64-114.
Page JK (1961) The estimation of monthly mean values of daily total short wave radiation on vertical and inclined surfaces from sunshine records for latitudes 400 N–400 S. In: Proceedings of UN Conference on New Sources of Energy 4: 378-390.
Muzathik AM, Ibrahim MZ, Samo KB, Wan Nik WB (2011) Estimation of global solar irradiation on horizontal and inclined surfaces based on the horizontal measurements. Energy 38: 812-818.
Kambezidis HD, Psiloglou BE (2008) the meteorological radiation model: advancements and application. In: Badescu V, (ed), Modeling solar radiation at the earth’s surface, Springer, Verlag.
Khalil SA, Fathy AM (2008) An empirical method for estimating global solar radiation over Egypt, Acta Polytechnica 5: 48-53.
Kadir B (2009) Correlations for estimation of daily global solar radiation with hours of bright sunshine in Turkey. Energy 34: 485-501
Bahel V, Srinivasan R, Bakhsh H (1987) Statistical comparison of correlations for estimation of global horizontal solar radiation. Energy 12: 1309-1316.
Akinoglu BG, Ecevit A (1990) Construction of a quadratic model using modified Ångström coefficients to estimate global solar radiation. Solar Energy 45: 85-92.
Fletcher AL (2007) Estimating daily solar radiation in New Zealand using air temperatures. New Zealand Journal of Crop Horticultural Science 35: 147-157
Shafiqur R (1998) Solar radiation over Saudi Arabia and comparisons with empirical models. Energy 23: 1077-1082.
Rietveld MR (1978) A new method for estimating the regression coefficients in the formula relating solar radiation to sunshine. Agricultural Meteorology 19: 243-252.
Alnaser WE (1993) New model to estimate the solar global irradiation using astronomical and meteorological parameters. Renewable Energy 3: 175-177
Luis FZ, Lourdes R, Jesus P (2005) Artificial intelligence techniques applied to hourly global irradiance estimation from satellite-derived cloud index. Energy 30: 1685-1697.
Chibani CM (2001) Global solar radiation estimation in Algeria. Energy Convers Manage 42: 967-973.
El-Sebaii AA, Trabea AA (2005) Estimating global solar radiation on horizontal surfaces over Egypt. Egypt J Solids 28: 163-175.
Supit I, Van Kappel RR (1998) A simple method to estimate global radiation, Solar Energy 63: 147-160.
Halouani N, Nguyen CT, Vo-Ngoc D (1993) Calculation of monthly average global solar radiation on horizontal surfaces using daily hours of bright sunshine, Solar Energy 50: 247-258.
Gopinathan KK (1998) A general formula for computing the coefficients of the correlation connecting global solar radiation to sunshine duration. Solar Energy 41: 499-502
Sabziparavar AA, Shetaee H (2007) Estimation of global solar radiation in arid and semi-arid climates of east and west Iran. J Sol Energy 32: 649-655.
Jacovides CP (2006) Comparative study of various correlations in estimating hourly diffuse fraction of global solar radiation. Renew Energy 31: 2492-2504.
Kamali GH, Moradi AI, Khalidi A (2006) Estimating solar radiation on titled surfaces with various orientations: A case study in Karaj (Iran). Theor Appl Climatol 84: 235-241.
Muneer T, Saluja GS (1985) A brief review of models for computing solar radiation on inclined surfaces. Energy Convers Manage 25: 443-458.
Diez-Mediavilla M, Miguel AD, Bilbao J (2005) Measurement and comparison of diffuse solar irradiance models on inclined surfaces in Valladolid (Spain). Energy Convers Manage 46: 2075-2092.
Notton G, Poggi P, Cristofari C (2006) Predicting hourly solar irradiations on inclined surfaces based on the horizontal measurements: performances of the association of well-known mathematical models. Energy Convers Manage 47: 1816-1829.
Martínez-Durbán M, Zarzalejo LF, Bosch JL, Rosiek S, Polo J, et al. (2009) Estimation of global daily irradiation in complex topography zones using digital elevation models and meteosat images: comparison of the results. Energy Convers Manage 50: 2233-2238.
Perez R, Ineichen P, Seals R, Michalsky J, Stewart R (1990) Modeling daylight availability and irradiance components from direct and global irradiance. J Solar Energy 44: 271-289.
Kreider J, Kreith F (1981) Solar energy handbook, New York, USA p: 362.
Angström A (1956) On the computation of global radiation from RECP: ords of sunshine. Arkiv Geof 2: 471-479.
Sopian K, Othman MYHJ (1992) Estimates of monthly average daily global solar radiation in Malaysia. J Renew Energy 2: 319-325.
Janjai S, Praditwong P, Moonin C (1996) A new model for computing monthly average daily diffuse radiation for Bangkok. Renew Energy 9: 1283-1286.
Sben Z, Tan E (2001) Simple models of solar radiation data for northwestern part of Turkey. Energy Convers Manage 42: 587-598.
Chineke T (2008) Equations for estimating global solar radiation in data sparse regions. J Renew Energy 33: 827-831.
Yohanna J, Itodo I, Umogbai V (2011) A model for determining the global solar radiation for Makurdi, Nigeria. J Renew Energy 36: 1989-1992.
Khatib T, Mohamed A, Mahmoud M, Sopian K (2011) Modeling of daily solar energy on a horizontal surface for five main sites in Malaysia. Int J Green Energy 8: 795-819.
Abdalla Y, Baghdady M (1985) Global and diffuse solar radiation in Doha (Qatar). J Solar Wind Technol 2: 209-212.
Benson R, Paris M, Sherry J, Justus C (1984) Estimation of daily and monthly direct, diffuse and global solar radiation from sunshine duration measurements. J Solar Energy 32: 523-535.
Trabea A (2000) Analysis of solar radiation measurements at Al-Arish area, North Sinai, Egypt. J Renew Energy 20: 109-125.
Top S, Dilma U, Aslan Z (1995) Study of hourly solar radiation data in Istanbul. J Renew Energy 6: 171-174.
El-Sebaii A, Al-Hazmi F, Al-Ghamdi A, Yaghmour S (2010) Global direct and diffuse solar radiation on horizontal and tilted surfaces in Jeddah, Saudi Arabia. Appl Energy 87: 568-576.
Collares-Pereira M, Rabl A (1979) The average distribution of solar radiation: correlations between diffuse and hemispherical and between daily and hourly insolation values. J Sol Energy 22: 155-164.
Tuller SE (1976) The relationship between diffuse, total and extra-terrestrial solar radiation. J Solar Energy 18: 259-263
Li H, Ma W, Wang X, Lian Y (2011) Estimating monthly average daily diffuse solar radiation with multiple predictors: A case study. J Renew Energy 36: 1944-1948.
Mohandes M, Rehman S, Halawani TO (1998) Estimation of global solar radiation using artificial neural networks. Renew Energy 14: 179-184.
Alawi SM, Hinai HA (1998) An ANN-based approach for predicting global radiation in locations with no direct measurement instrumentation. J Renew Energy 14: 199-204.
Mihalakakou G, Santamouris M, Asimakopoulos DN (2000) The total solar radiation time series simulation in Athens, using neural networks. Theore Appl Climatol 66: 185-197.
Dorvio ASS, Jervase JA, Al-Lawati A (2002) Solar radiation estimation using artificial neural networks. J Appl Energy 74: 307-319.
Sozen A, Ogblu EA, Ozalp M, Kany´t EG (2004) Use of artificial neural networks for mapping the solar potential in Turkey. Appl Energy 77: 273-286.
Fadare D (2009) Modelling of solar energy potential in Nigeria using an artificial neural network model. Appl Energy 86: 1410-1422.
Lam J, Wan K, Yang L (2008) Solar radiation modeling using ANNs for different climates in China. Energy Convers Manage 49: 1080-1090.
Mellit A, Kalogirou S, Shaari S, Salhi H, Arab A (2008) Methodology for predicting sequences of mean monthly clearness index and daily solar radiation data in remote areas: Application for sizing a stand-alone PV system. J Renew Energy 33: 1570-1590.
Reddy K, Ranjan M (2003) Solar resource estimation using artificial neural networks and comparison with other correlation models. Energy Convers Manage 44: 2519-2530.
Benghanem M, Mellit A (2010) Radial basis function network-based prediction of global solar radiation data: application for sizing of a stand-alone photovoltaic system at Al-Madinah, Saudi Arabia. J Renew Energy 35: 3751-3562.
Khatib T, Mohamed A, Sopian K, Mahmoud M (2011) Modeling of solar energy for Malaysia using artificial neural networks. In: The 11th WSEAS/IASME International Conference on Electric Power Systems, High Voltages and Electric Machines pp: 486-489.
Hontoria L, Aguilera J, Zufiria P (2005) An application of the multilayer perceptron: solar radiation maps in Spain. J Sol Energy 79: 523-530.
Zarzalejo L, Ramirez L, Polo J (2005) Artificial intelligence techniques applied to hourly global irradiance estimation from satellite-derived cloud index. J Energy 30: 1685-1697.
Samy A, Khalil A, Shaffie M (2016) Evaluation of transposition models of solar irradiance over Egypt. Renewable and Sustainable Energy Reviews 66: 105-119.
Bird RE, Riordan CJ (1986) Simple solar spectral model for direct and diffuse irradiance on horizontal and tilted planes at the Earth’s surface for cloudless atmosphere. J Climate Appl Meteorol 25: 87-97.
Khalil A, Samy A, Shaffie M (2013) Performance of statistical comparison models of solar energy on horizontal and inclined surface. Int J Energy Power 2: 1.
Samy A, khalil A, Shaffie M (2013) A comparative study of total, direct and diffuse solar irradiance by using different models on horizontal and inclined surfaces for Cairo, Egypt. Renewable and Sustainable Energy 27: 853-863.
Glover J, McCulloch JS (1958) The empirical relation between solar radiation and hours of sunshine. J of Royal Meteorological Society 84: 172-175.
Iqbal M (1983) An introduction to solar radiation. Academic Press, New York, USA.
Saeed AAG, Ahmed MAL, Adel SN, El-Shahat FM, Ashraf SE (2016) Global Solar Radiation over Al-Baha City, KSA: Comparison of Predicted Models and Measured Data. International Journal of Engineering Science and Innovative Technology p: 5.
Saeed AAG, Ahmed MAL, Adel SN, El-Shahat FM, Ashraf SE (2017) Wind data analysis for Albaha city, Saudi Arabia. Journal of basic and applied sciences 1: 1-9.
Hamdy KE, Ahmed EG, El-Hussainy F, Hamid R, Beheary MM, et al. (2006) Optimum solar flat-plate collector slope: Case study for Helwan, Egypt. Energy Conversion and Management 47: 624-637.
Bird RE, Riordan CJ (1986) Simple solar spectral model for direct and diffuse irradiance on horizontal and tilted planes at the Earth’s surface for cloudless atmosphere. J Climate Appl Meteorol 25: 87- 97.
Spencer JW (1975) Fourier series représentation of the position of the sun. 2: 165-172.
Khatib T, Mohamed A, Sopian K (2012) A review of solar energy modeling techniques. Renewable and Sustainable Energy Reviews 16: 2864-2869.

Citation: Khalil SA, Aly HAS (2018) Comparative and Evaluate of Empirical Models for Estimation Global Solar Radiation in Al-Baha, KSA. J Earth Sci Clim Change 9: 492. DOI: 10.4172/2157-7617.1000492

Copyright: © 2018 Khalil SA, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Journal of Earth Science & Climatic Change
Open Access