Research Article Open Access
Chemometrical Evaluation of Metoprolol Tartarate Enantiomers Separation Applying Conventional Achiral Chromatography
Ivkovic B1*, Karljikovic-Rajic K2, Vujic Z1 and Ibric S3
1Department of Pharmaceutical Chemistry and Drug Analysis, Faculty of Pharmacy, University of Belgrade, Serbia
2Department of Analytical Chemistry, Faculty of Pharmacy, University of Belgrade, Serbia
3Department of Pharmaceutical Technology and Cosmetology, University of Belgrade, Serbia
- *Corresponding Author:
- Branka Ivkovic
Department of Pharmaceutical Chemistry and Drug Analysis
Faculty of Pharmacy, University of Belgrade
Vojvode Stepe 450, 11221 Belgrade-Kumodraz
PO Box 146, Serbia
Tel:+381113951335
Fax: +381113972840
E-mail: blucic@pharmacy.bg.ac.rs
Received Date: January 27, 2016; Accepted Date: February 24, 2016; Published Date: March 04, 2016
Citation: Ivkovic B, Karljikovic-Rajic K, Vujic Z, Ibric S (2016) Chemometrical Evaluation of Metoprolol Tartarate Enantiomers Separation Applying Conventional Achiral Chromatography. J Anal Bioanal Tech 7:303. doi:10.4172/2155-9872.1000303
Copyright: © 2016 Ivkovic B, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Analytical & Bioanalytical Techniques
Abstract
In this paper, the separation of metoprolol tartarate enantiomers using conventional achiral chromatography was followed employing experimental design 24. Design was useful tool in evaluation of chromatographic behavior of enantiomers. For the separation, Supelcosil LC18 4.6 mm × 250 mm, 5 m particle size column was used. UV detection was performed at 275 nm. Because of the large number of factors which can influence chromatographic separation, in preliminary study ″one factor at a time″ method was applied to define values of important factors. As outputs, retention factor, selectivity factor and resolution factors were chosen. Chromatographic behavior of investigated enantiomers was affected by acetonitrile content, chiral modificator content in the mobile phase and flow rate the most, demonstrated by obtained linear models. On the basis of results from screening of experiment, factors with strong influence on the separation, were analyzed in method optimization applying response surface methodology (RSM). The appropriate region of chromatographic behavior of metoprolol tartarate enantiomers was defined using three-D graphs and analysis of variance. The methodology proposed represents an efficient approach in resolving the problem of searching for optimal HPLC chromatographic conditions via experimental design.
Keywords
Metoprolol tartarate; Enantiomers; RP-HPLC; Experimental design
Introduction
Metoprolol tartarate ((R,S)–3[4–(2–methoxyethyl) phenoxy)–1– (isopropylamino) propan–2–ol] tartarate) is a β1-adrenoreceptor antagonist (β1-blocker) widely used in the treatment of hypertension, angina pectoris and cardiac dysrhythmias [1,2].
Most β-adrenergic antagonists (β-blockers) are therapeutically used as a racemic mixture and their enantiomers demonstrate different pharmacodynamic and pharmacokinetic properties [1,2]. The both enantiomers are reducing blood pressure, but the therapeutic effects of the (S)-enantiomer is about 100 times stronger than (R)-enantiomer. The increasing demands for the production of enantiomerically pure drugs have led to enantioselective separations becoming one of the most important analytical tasks. In this context, enantioselective HPLC is one of the most powerful and widely employed separation techniques, both for analytical and preparative purposes, as well as for research in pharmaceutical and biomedical analysis.
Separation of β1-blocker enantiomers included conventional achiral chromatography with pre-column derivatisation [3,4]. Using different chiral stationary phases or chemically different chiral mobile phase additives, β-blockers has been recently separated [5-8]. Also, the spectrophotometric method for analysis of β-cyclodextrin/metoprolol tartarate inclusion complex was investigated [9].
The aim of our investigation was analysis of metoprolol tartarate enantiomers using achiral stationary phase with β-cyclodextrin as chiral additive in the mobile phase. The experimental design was applied as the best way to define chromatographic behavior of enantiomers. Analysis employed ″one factor at a time″ method for preliminary study, full factorial design for screening of experiment and response surface methodology (RSM) for method optimization. A literature search showed many experimental design applications in analytical method development and validation, especially in the area of separation science. Experimental design has been used for separation optimization [10-12] and for validation in RP-HPLC method [13,14]. It was used for robustness testing in RP-HPLC method [15,16] and capillary electrophoresis [17]. The methodology proposed in this paper represents novel, efficient and easily attainable approach in resolving metoprolol tartarate enantiomers using conventional achiral chromatography.
Experimental
Reagents and samples
All reagents used were of an analytical grade. Methanol-gradient grade (Merck, Darmstadt, Germany), acetonitrile (Merck, Darmstadt, Germany), water-HPLC grade, triethylamine (TEA) (Merck, Darmstadt, Germany). Beta cyclodextrine (-CD) was obtained from Cyclolab, Hungary. Presolol® tablets (containing 100 mg of metoprolol taratarat) were manufactured by Hemofarm d.o.o., SCG. Working standard of metoprolol tartarate was obtained from Hemofarm d.o.o., SCG.
Chromatographic conditions
The chromatographic system Hewlett Packard 1100 (Agilent, Technologies) consisted of a HP 1100 pump, HP 1100 UV-VIS detector and HP ChemStation integrator. Separations were performed on a Supelcosil LC18 4.6 mm × 250 mm, 5 μm particle size column. UV detection was performed at 275 nm. The samples were introduced through a Rheodyne injector valve with a 20 μL sample loop
Buffer solution
Buffer solution was prepared by adding of 2 ml of TEA to 600 ml of HPLC water, pH was adjusted in the range from 2 to 6 with glacial acetic acid.
Solution for equlibration and storage of column
Solution was prepared in concentration of 3 mM of β-CD in water.
Results and Discussion
In preliminary investigations, influence of different chromatographic factors on separation of metoprolol tartarate enantiomers was analyzed. As the separation was performed employing conventional achiral chromatography, beta cyclodextrine (β-CD) was added to the mobile phase as chiral modificator. Mobile phases consisted of acetonitrile and β-CD in triethylamine/glacial acetic acid buffer in different ratios. Column was stored and conditioned with solution of 3 mM of β-CD in water. In chromarography many factors can influence separation e.g., content of organic modifier in mobile phase, pH of the mobile phase, column temperature, flow rate, concentration of solute etc. In the first step of our study, pH of the mobile phase and temperature were defined using "one factor at a time" method. pH of the mobile phase (2.5; 3.0; 4.0; 5.0 and 6.0) was changed and other factors were kept at constant level. Obtained chromatograms demonstrated the best separation of enantiomers at pH 3.0 and in following investigations it remained constant. Secondly, temperature was analyzed on two levels 30°C and 40°C. The accepted separation was at 35°C column temperature.
In the second step, for the screening of experiment, full factorial design 24 was chosen. Full factorial designs at two levels are mainly used for screening, that is, to determine the influence of a number of effects on a response and to eliminate those that are not significant [18]. Selected factors and their "low" (–) and "high" (+) levels are presented in Table 1. Matrix of the experiment is given in Table 2.
| Factors | Levels of the investigation | ||
|---|---|---|---|
| (-) | (+) | ||
| X1 | Acetonitrile (%) | 9.1 | 14.5 |
| X2 | β–CD (mM) | 5.81 | 8.81 |
| X3 | Flow rate (mlmin-1) | 1 | 1.5 |
| X4 | Concentration of metoprolol tartarate (mlL-1) | 0.25 | 0.50 |
(-) and (+) are “low” and ”high” levels
Table 1: Factor and their levels.
| Number of experiments | X1 | X2 | X3 | X4 |
|---|---|---|---|---|
| 1 | - | - | - | - |
| 2 | + | - | - | - |
| 3 | - | + | - | - |
| 4 | + | + | - | - |
| 5 | - | - | + | - |
| 6 | + | - | + | - |
| 7 | - | + | + | - |
| 8 | + | + | + | - |
| 9 | - | - | - | + |
| 10 | + | - | - | + |
| 11 | - | + | - | + |
| 12 | + | + | - | + |
| 13 | - | - | + | + |
| 14 | + | - | + | + |
| 15 | - | + | + | + |
| 16 | + | + | + | + |
Table 2: Matrix for screening of experiment.
As outputs (Y) capacity factors (k1 (Y1)-retention factor for enantiomer R (+), k2 (Y2)-retention factor for enantiomer S (-)), selectivity factor (α–Y3) and resolution factor (Rs–Y4) were analyzed. The obtained results are presented in Table 3.
| Number of exp | k1 (Y1) | k2 (Y2) | a (Y3) | Rs (Y4) |
|---|---|---|---|---|
| 1 | 1.03 | 1.17 | 1.13 | 0.96 |
| 2 | 0.75 | 0.85 | 1.14 | 0.94 |
| 3 | 1.03 | 1.17 | 1.14 | 0.93 |
| 4 | 0.68 | 0.77 | 1.13 | 0.93 |
| 5 | 1.03 | 1.18 | 1.15 | 0.96 |
| 6 | 0.73 | 0.84 | 1.16 | 0.94 |
| 7 | 1.03 | 1.18 | 1.15 | 0.96 |
| 8 | 0.70 | 0.80 | 1.14 | 0.94 |
| 9 | 1.03 | 1.17 | 1.13 | 0.98 |
| 10 | 0.75 | 0.85 | 1.14 | 0.94 |
| 11 | 1.03 | 1.17 | 1.14 | 0.93 |
| 12 | 0.68 | 0.77 | 1.13 | 0.93 |
| 13 | 1.03 | 1.18 | 1.15 | 0.95 |
| 14 | 0.73 | 0.84 | 1.16 | 0.94 |
| 15 | 1.03 | 1.18 | 1.15 | 0.97 |
| 16 | 0.70 | 0.80 | 1.14 | 0.95 |
Table 3: Results for outputs.
In experimental design for the evaluation of influence of investigated factors, on measured response, mathematical model was applied. Often form of a mathemathical model is:
y=b0+b1x1+b2x2+b3x3+ …+bN-1xN-1+bNxN+b12x1x2+b13x1x3+b23x2x3+…+b(N-1)NxN-1xN (Eq. 1)
where y presents the estimate response, b0, is the average experimental response, the coefficients b1 to bN are the estimated effects of the factors considered and the extend to which these terms affect the performance of the method is called main effect. The coefficients b12 to b(N-1)N are called the interaction terms. We can see that the factorial design provides information about the importance of interaction between the factors [18]. The calculating coefficients of mathematical models for outputs are presented in Table 4.
| Number of exp | k1 | k2 | a | Rs |
|---|---|---|---|---|
| b1 | -0.315 | -0.36 | 0 | -0.01625 |
| b2 | -0.025 | -0.03 | -0.005 | -0.00875 |
| b1b2 | -0.025 | -0.03 | -0.01 | 0.00625 |
| b3 | 0.00000 | 0.01000 | 0.01500 | 0.00875 |
| b1b3 | -4.16334E-17 | -1.38778E-17 | 0 | -0.00125 |
| b2b3 | 0.01 | 0.01 | -0.005 | 0.01625 |
| b1b2b3 | 0.01 | 0.01 | 0 | -0.00875 |
| b4 | 0 | 5.55112E-17 | -3.60822E-16 | 0.00375 |
| b1b4 | 1.38778E-17 | -6.93889E-17 | 0 | -0.00125 |
| b2b4 | 0 | 0 | -2.77556E-17 | 0.00125 |
| b1b2b4 | 0.01 | 0.01 | 0 | -0.00875 |
| b3b4 | 0 | 5.55112E-17 | -2.77556E-17 | -0.00125 |
| b1b3b4 | 1.38778E-17 | -1.38778E-17 | 0 | 0.00375 |
| b2b3b4 | 0 | 0 | 2.77556E-17 | 0.00625 |
| b1b2b3b4 | 0 | -1.38778E-17 | 0 | -0.00375 |
| b0 | 0.8725 | 0.995 | 1.1425 | 0.946875 |
Table 4: Coefficients for mathematical models.
The results showed that acetonitrile content and concentration of β-CD had the biggest influence on retention factors (Y1 and Y2). The flow rate and content of β-CD influenced selectivity factor (Y3) and resolution (Y4) the most. Concentration of metoprolol tartarate had negligible influence on analyzed outputs and in further investigations it was kept constant.
In the third step of method optimization, three factors (content of acetonitrile, content of -CD and flow rate) were analyzed in 22 experiments. Matrix of experiment for optimization is presented in Table 5. Experimental data for outputs are presented in Table 6.
| Number of exp. | X1 | X2 | X3 |
|---|---|---|---|
| 1 | - | - | - |
| 2 | 0 | - | - |
| 3 | + | - | - |
| 4 | - | 0 | - |
| 5 | 0 | 0 | - |
| 6 | + | 0 | - |
| 7 | - | + | - |
| 8 | 0 | + | - |
| 9 | + | + | - |
| 10 | - | - | + |
| 11 | 0 | - | + |
| 12 | + | - | + |
| 13 | - | 0 | + |
| 14 | 0 | 0 | + |
| 15 | + | 0 | + |
| 16 | - | + | + |
| 17 | 0 | + | + |
| 18 | + | + | + |
| 19 | 0 | 0 | - |
| 20 | 0 | 0 | - |
| 21 | 0 | 0 | + |
| 22 | 0 | 0 | + |
Table 5: Matrix of experiment for optimization.
| Number of exp | k1 (Y1) | k2 (Y2) | a (Y3) | Rs (Y4) |
|---|---|---|---|---|
| 1 | 1.03 | 1.17 | 1.13 | 0.96 |
| 2 | 1.05 | 1.18 | 1.12 | 0.68 |
| 3 | 0.75 | 0.85 | 1.14 | 0.94 |
| 4 | 1.31 | 1.48 | 1.13 | 0.72 |
| 5 | 1.05 | 1.19 | 1.13 | 0.67 |
| 6 | 1.14 | 1.28 | 1.12 | 0.68 |
| 7 | 1.03 | 1.17 | 1.14 | 0.93 |
| 8 | 1.05 | 1.18 | 1.13 | 0.67 |
| 9 | 0.68 | 0.77 | 1.13 | 0.93 |
| 10 | 1.03 | 1.18 | 1.15 | 0.96 |
| 11 | 1.1 | 1.23 | 1.12 | 0.67 |
| 12 | 0.73 | 0.84 | 1.16 | 0.94 |
| 13 | 1.32 | 1.51 | 1.14 | 0.72 |
| 14 | 1.09 | 1.23 | 1.13 | 0.67 |
| 15 | 1.15 | 1.31 | 1.14 | 0.67 |
| 16 | 1.03 | 1.18 | 1.15 | 0.96 |
| 17 | 1.03 | 1.17 | 1.14 | 0.67 |
| 18 | 0.7 | 0.8 | 1.14 | 0.94 |
| 19 | 1.04 | 1.2 | 1.13 | 0.66 |
| 20 | 1.05 | 1.19 | 1.13 | 0.67 |
| 21 | 1.1 | 1.22 | 1.13 | 0.67 |
| 22 | 1.09 | 1.23 | 1.13 | 0.66 |
Table 6: Results of experiment for optimization.
On the basis of the results, outputs Y1 and Y4 were chosen to analyze separation. The results for others outputs gave bad coefficient of determination (≤ 0.5) and they fitted badly in the obtained model. Those results could be explained with different characters of metoprolol tartarate enantiomers. The results for analysis of variance concerning influence of acetonitrile content and β-CD content, as the most important inputs, are presented in Table 7 for output Y1 and in Table 8 for output Y4.
| Source of variation | Sum of squares | d.f. | Mean square | F-ratio | F-tab |
|---|---|---|---|---|---|
| X1 | 0.21333333 | 1 | 0.2133333 | 22.15 | F1,18=1.14 |
| X2 | 0.00240833 | 1 | 0.0024083 | 0.25 | |
| X12 | 0.41423037 | 1 | 0.41423037 | 21.15 | |
| X22 | 0.21781833 | 1 | 0.2178183 | 22.61 | F3,18=3.16 |
| F15.3=8.70 | |||||
| Model | 0.43356000 | 3 | 0.1445184 | 15.0029 | |
| Error | 0.173390 | 18 | 0.00963278 | ||
| Lack of fit | 0.05539 | 15 | 0.00369 | 5.594 | |
| Purely experimental uncertainty | 0.01800 | 3 | 0.00066 | ||
| Total (corr) | 0.59814 | 21 | |||
| R2 | 0.7143 | ||||
Table 7: Analysis of variance for variables and for the full regression for retention factor (k’1).
| Source of variation | Sum of squares | d.f. | Mean square | F-ratio | F-tab |
|---|---|---|---|---|---|
| X1 | 0.00187500 | 1 | 0.00187500 | 0.42 | F1,17=1.45 |
| X2 | 0.00020833 | 1 | 0.00020833 | 0.05 | |
| X12 | 0.20423045 | 1 | 0.20423045 | 46.19 | |
| X22 | 0.08965974 | 1 | 0.08965974 | 20.28 | F4,17=2.96 |
| F14.3=8.71 | |||||
| Model | 0.29597352 | 4 | 0.0739934 | 16.7335 | |
| Error | 0.0751719 | 17 | 0.00442188 | ||
| Lack of fit | 0.05171 | 14 | 0.004083 | 0.6805 | |
| Purely experimental uncertainty | 0.01800 | 3 | 0.00600 | ||
| Total (corr) | 0.44086 | 21 | |||
| R2 | 0.7974 | ||||
Table 8: Analysis of variance for variables and for the full regression for resolution factor (Rs).
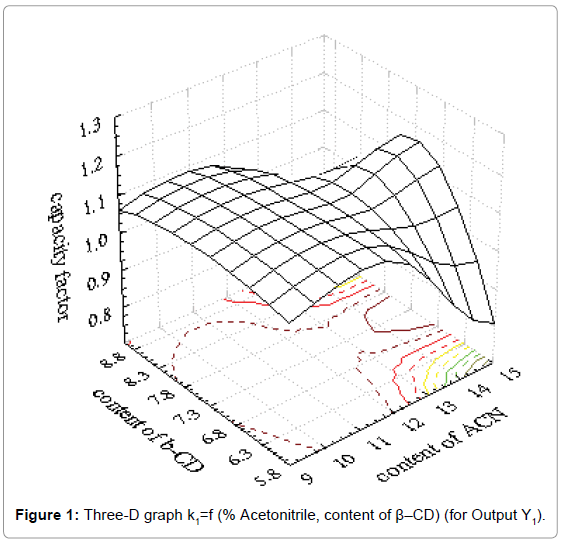
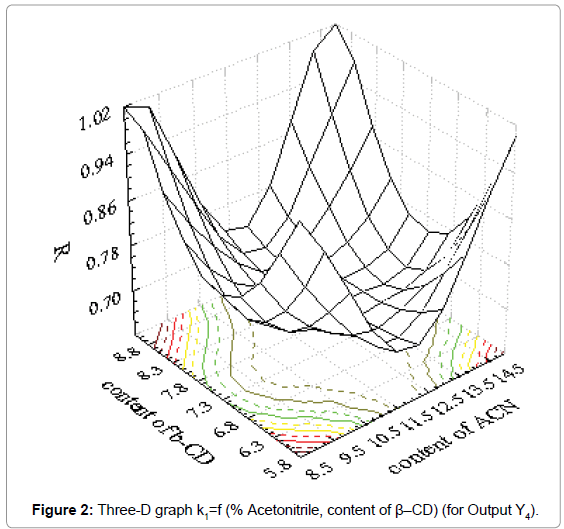
Coefficients of determination (R2) and results for factor Fisher value (F) demonstrated good fitting of obtained results in mathematical model. Suitable three-D graphs are presented in Figure 1 for output Y1 and in Figure 2 for output Y4.
Obtained three-D graphs gave information about influence of acetonitrile content and chiral modificator concentration on metoprolol tartarate enantiomers separation. The connection between influence of the factors and outputs can be presented with second order polynoms. The obtained polynoms are presented as Equation 2 and Equation 3.
Y1=-3.585+0.059x1+1.288x2-0.004x12-0.003x1x2-0.086x22 (Eq. 2)
where is Y1-is retention factor of enantiomer R (+)
Y4=6.918-0.52x1-0.875x2+0.022x12+0.001x1x2+0.059x22 (Eq. 3)
where is Y4-is resolution factor
As it could be seen from the Figure 1, retention factor of the first enantiomer has a higher value for higher content of β-CD and higher content of acetonitrile. Also, strong influence of acetonitrile content is obvious and drastical decrease of retention factor was observed. On the other hand, resolution factor is under strong influence of both investigated factors. It is clear that both factors must be carefully set in order to achieve acceptable separation of enantiomers investigated.
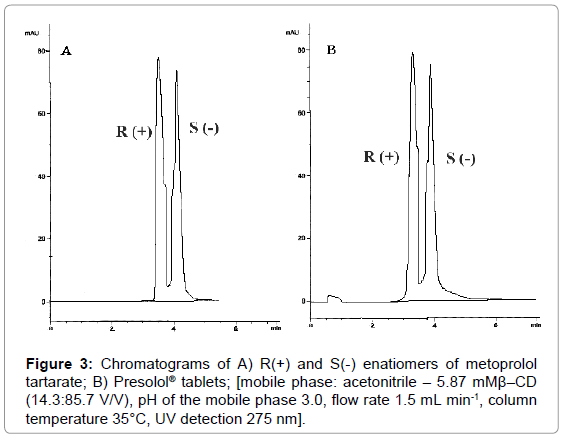
According to the presented results the best separation of metoprolol tartarate enantiomers can be achieved with mobile phase: acetonitrile-5.87 mM β-CD (14.3:85.7), pH of the mobile phase adjusted to 3.0 and flow rate 1.5 ml min-1 at 35°C column temperature. Under these conditions the value of the resolution factor is 0.98. The representative chromatograms are presented in Figure 3.
Conclusion
Applying experimental design it was possible to achieve optimal separation of metoprolol tartarate enantiomers performing a relatively small number of experiments. In this paper full factorial design 24 was used for experiment screening. Chromatographic behavior of investigated enantiomers was affected by acetonitrile content, chiral modificator content in the mobile phase and flow rate the most, which was demonstrated by obtained linear models. After experimental screening, RSM was used for optimization of RP–HPLC method and optimal chromatographic conditions were settled. The proposed methodology represents an efficient and easily attainable approach in resolving the problem of searching for optimal HPLC chromatographic conditions via experimental design.
Acknowledgements
Our work was supported by the Scientific Research Grants from the Ministry of Science and Technology OI172041 (Serbia).
References
- Gisvold O, Delgado JN, Remers WA (1998) Wilson and Gisvold’s Textbook of Organic Medicinal and Pharmaceutical Chemistry. Lippincott-Raven, Philadelphia, New York, pp: 498-503.
- Foye WO, Lemke TL, Williams DA (1995) Principles of Medicinal Chemistry. Williams and Wilkins, Baltimore, pp: 359-379.
- Kleidernigg OP, Posch K, Lindner W (1996) Synthesis and application of a new isothiocyanate as a chiral derivatizing agent for the indirect resolution of chiral amino alcohols and amines. J Chromatogr A 729: 33-42.
- Olsen L, Bronnumhansen K, Helboe P, Jorgensen GH, Kryger S (1993) Chiral separations of ß-blocking drug substances using derivatization with chiral reagents and normal-phase high-performance liquid chromatography. J Chromatogr 636: 231-241.
- Hedeland M, Isaksson R, Pettersson C (1998) Cellobiohydrolase I as a chiral additivein capillary electrophoresis and liquid chromatography. J Chromatogr A 807: 297-305.
- Aboulenein HY, Abou-Basha LI (1996) HPLC Separation of Nadolol and Enantiomers on Chiralcel OD Column. J Liq Chromatogr Relat Tehnol 19: 383-392.
- Piperaki S, Tsantilikakoulidou A, Parissi-Polou M (1995) Solvent selectivity in chiral chromatography using a ß-cyclodextrin-bonded phase. Chirality 7: 257-266.
- Egginger G, Lindner W, Vandebosch C, Massart DL (1993) Enantioselective bioanalysis of beta-blocking agents: Focus on atenolol, betaxolol, carvedilol, metoprolol, pindolol, propranolol and sotalol. Biomed Chromatogr 7: 277-295.
- Radulovic DM, Karljikovic-Rajic KD, Lucic BM, Vujic ZB (2001) A preliminary study of ß-cyclodextrin/metoprolol tartrate inclusion complex for potential enantiomeric separation. J Pharm Biomed Anal 24: 871-876.
- Araujo P (2000) A new high performance liquid chromatography multifactor methodology for systematic and simultaneous optimisation of the gradient solvent system and the instrumental/experimental variables. Trends Anal Chem 19: 524-529.
- Gennaro MC, Marengo E, Gianotti V, Angioi S (2002) Simultaneous reversed-phase high-performance liquid chromatographic separation of mono-, di-and trichloroanilines through a gradient elution optimised by experimental design. J Chromatogr A 945: 287-292.
- Medenica M, Jancic B, Ivanovic D, Malenovic A (2004) Experimental design in reversed-phase high-performance liquid chromatographic analysis of imatinib mesylate and its impurity. J Chromatogr A 1031: 243-248.
- Ye C, Liu J, Ren F, Okafo N (2000) Design of experiment and data analysis by JMP (SAS institute) in analytical method validation. J Pharm Biomed Anal 23: 581-589.
- Ficarra R, Ficarra P, Tommasini S, Melardi S, Calabro ML, et al. (2000) Validation of a LC method for the analysis of zafirlukast in a pharmaceutical formulation. J Pharm Biomed Anal 23: 169-174.
- Vander Heyden Y, Nijhuis A, Smeyers-Verbeke J, Vandeginste BG, Massart DL (2001) Guidance for robustness/ruggedness tests in method validation. J Pharm Biomed Anal 24: 723-753.
- Hund E, Vander Heyden Y, Haustein M, Massart DL, Smeyers-Verbeke J (2000) Robustness testing of a reversed-phase high-performance liquid chromatographic assay: comparison of fractional and asymmetrical factorial designs. J Chromatogr A 874: 167-185.
- Fabre H (1996) Robustness testing in liquid chromatography and capillary electrophoresis. J Pharm Biomed Anal 14: 1125-1132.
- Deming SN, Morgan SL (1993) Experimental design: a chemometrical approach. Elsevier, Amsterdam, pp: 317.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 10923
- [From(publication date):
April-2016 - Apr 02, 2025] - Breakdown by view type
- HTML page views : 10053
- PDF downloads : 870