Assessment of the Category of Technical Condition and Seismic Stability of Historic Structures Using the Method of Dynamic Geophysical Tests.
Received: 07-Sep-2018 / Accepted Date: 29-Sep-2018 / Published Date: 07-Oct-2017 DOI: 10.4172/2168-9717.1000214
Abstract
Protection of historical buildings is an important international task. Historical buildings, in addition to aging wear, are subjected to periodic and continuous dynamic effects from earthquakes and passing by road and rail transport and from effects of exhaust gases. Most historical objects are constructively made of local materials: adobe, brick and stone blocks, they have mixed structural schemes and do not possess the necessary seismic resistance. The authors of this article propose the technology of dynamic and geophysical testing of structures for assessing the category of technical condition and seismic stability. This article gives examples of the application of this technology to assess the state of historical objects.
Keywords: Buildings; History; Earthquakes; Seismic; Seismic wave
Introduction
Builders of historical buildings, as they could, tried to resist the destructive effects of static and dynamic loads. To increase the stability and seismic stability of structures they invented original design solutions, while harmoniously used ground and local conditions. To protect against earthquakes, they skillfully used the terrain and ground conditions [1-3]. For example, structures were equipped with ditches around them, or multi-layered foundations were used to protect the structures from seismic waves. An interesting fact is that most of the historical buildings that have survived in our time are on hills and have strong [4-6] rocky grounds at the base. One of such ancient structures on a rocky hill is the Antique Temple Parthenon in Athens. The temple was built on a high rocky hill, and the dimensions of the hill along the length, width and height are proportional to the size of the structure and about 4 times larger than the size of the temple [7-9].
The ancient builders paid much attention to the geometric proportions of the structures [1] When designing structures, they took into account the proportions of the hills on which the construction was erected. In the case of the Parthenon, the size of the hill is proportional to the size of the temple. Since the dynamics of the structure depends not only on its dimensions but also on its design and strength. The value that takes into account the geometric and strength parameters of the structure is called rigidity (Figure 1) [2-6].
Significance of Rigidity
The builders of historical buildings apparently understood well the significance of rigidity on the bearing capacity of structures and their seismic resistance. In addition, they used certain principles to reduce the seismic effect transmitted through the soil to structures they created, structures whose structural systems proportionally combined mass and rigid parameters. It is clear that the constructive solution of the structure depended on its dimensions. Sensitive parameters of rigidity of constructive systems are oscillations. The vibrations of the structure depend on its mass and rigidity.
The solution of the differential equation describing the oscillations of a beam of length L has the following form [5,6]:
 (1),
(1),
Where,
T1: Period of oscillation of the beam, sec;
l: Length of the beam, m;
m: Mass per unit length of the beam, kg/m;
E: Modulus of elasticity, N/m2;
J: Moment of inertia of the beam section, m4.
Examples of Calculations and Experimentally Obtained Values of the Periods of Natural Oscillations of Structures and Soils at their Base
The author suggests for engineering calculations, to determine the normative values of the periods of oscillations of structures of different design in accordance with the following empirical dependence:
 (2),
(2),
Where,
D: Length of the side of the structure in the horizontal plane, along which the period of oscillations is determined, m;
H: Height of the structure, m;
k: Coefficient that takes into account the structural design of the structure, for a block structure, equal to 0.3;
g: Acceleration of gravity, m/s2 (Figure 2 and Table 1).
| № | Name of the structure | Length of the structure (x), m | Width of the structure (y), m | Height of the structure (h), m | The period of oscillation along the X axis (Tx), s | The period of oscillations along the Y (Ty) axis, s | The period of oscillation along the Z axis (Tz), s |
|---|---|---|---|---|---|---|---|
| 1 | The Parthenon in Greece | 69,5 | 30,9 | 13,7 | 0,16 | 0,24 | 0,4 |
| 1.1 | The hill on which the Parthenon is built | 278 | 123,6 | 54,8 | 0,77 | 1,38 | 1,15 |
| 2 | Ancient Temple Garni Armenia | 15,7 | 11,5 | 12 | 0,3 | 0,34 | 0,16 |
| 2.1 | The predominant period of natural oscillation of soils in Garni (obtained experimentally) | 0,625 | 0,625 | - | |||
| 3 | Church of Santa Maria del Suffrajo in the town of Aquila in the Republic of Italy | 22 | 17 | 15,4 | 0.32 | 0,36 | 0,7 |
| 3.1 | The prevailing period of natural oscillation of soils in the city of Aquila (obtained experimentally) | 0,3 | 0,1 | 0,5 | |||
| 4 | The Church of St. John in León, the Republic of Nicaragua | 25 | 23 | [9,7], (19,55)* |
[0,14], 0,24 |
[0,21], 0,33 |
[0,3], 0,26 |
| 4.1 | The predominant period of natural oscillation of soils near St. John's Church in Leon, Republic of Nicaragua | 0,22-0,5 | |||||
| 5 | Buddhist Temple in Nepal | 12,87 | 12,3 | 14 | 0,298 | 0,31 | 0,42 |
| 5.1 | The predominant period of the natural oscillation of the hill on which the temple is erected | 0,156 | 0,178 | 0,83 |
*The height of the bell tower is indicated in parentheses. The square brackets indicate the normative values of periods of natural oscillations of structures. Comparing the periods of natural oscillations of structures with the periods of oscillations of the soil massifs at their base it can be seen that the smaller the difference in the values of the periods of oscillations of soils and structures, the more damages the structure receives under dynamic impact.
Table 1: Periods of fluctuations in historical structures and ground hills at the base (normative and experimental values).
Measure for Assessing the Category of Technical Condition of Buildings by Comparing the Normative and Experimentally Obtained Values of the Periods of Natural Oscillations
The author suggests criteria by which you can determine the degree of damage to the structure. It is proposed to use a relative value indicating the percentage increase in the period of natural oscillations of the structure:
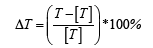 (3),
(3),
Where,
[T]: Normative value of the period of natural oscillations of the structure along the directions X, Y, Z;
T: Period of natural oscillations of the structure in the directions X, Y, Z (Table 2).
| Status Category | Increase in the period of natural oscillations, ΔТ,% | Degree of damage | Description of possible defects in bearing structures |
|---|---|---|---|
| 1 | to 10 | No damage, slight damage | Hair cracks are possible |
| 2 | to 30 | Moderate damage | Cracks up to 15 cm long. Reduction of strength up to 10%, traces of corrosion |
| 3 | to 60 | Strong damages | Reduction of the strength of masonry to 25%. Decrease the strength of concrete to 30%. Deflections of metal structures up to 1/150. Cracks intersecting up to 4-x rows of masonry. |
| 4 | to 90 | Heavy | Reduction of the strength of masonry to 50%. Cracks intersecting more than 4 rows of masonry. Deviation from the vertical is more than 1/50. Deflections of reinforced concrete beams more than 1/50, metal structures more than 1/75. |
| 5 | More than 90 | catastrophic | Collapse of individual parts, partial or complete collapse |
Table 2: Criteria for assessing the degree of damage to structures.
The greatest damages of the structure are expected at close values of the periods of natural oscillations of the soil base and the structure. To exclude resonant phenomena in the "soil-structure" system, the condition under which the oscillations created by the soil massifs should differ by 60% or more from the oscillations of the structure must be met. Such an example of collapse due to the coincidence of the values of the periods of oscillations of the soil and the structure and the insufficient rigidity of the structure to perceive the seismic load is the collapse of the dome of the Church of Santa Maria del Suffrajo in the town of Aquila in the province of Abruzzi in Italy.
For the construction of the Church of Santa Maria del Suffrajo in the city of Aquila in the Republic of Italy, the relationship between the periods of construction and soil is 1-1.6, which is less than 2 and corresponds to the resonant state, which apparently contributed to the collapse of the dome. Structures under the influence of seismic waves, have direction of motion of the wave. Traces of seismic waves on the stone pavement near the church showed that the waves moved parallel to the facade of the temple. Just the largest damage the dome received in the direction of motion of the front of seismic waves.
In contrast to the Italian temple, the Buddhist temple in Nepal, with strong seismic action, did not receive significant damage, its location on the rocky hill and the absence of resonance between the ground and the structure helped (Table 1 and Figures 3-7).
An Example of an Assessment of the Category of Technical Condition and Seismic Resistance of a Historical Structure
Let us consider an example of an assessment of the category of technical condition and seismic resistance of St. John's Catholic Church in Leon, Republic of Nicaragua (Figure 7) using dynamic-geophysical test data. The structure consists of a bell tower and a main block, there is a deformation seam between them. The foundation is ribbon, stone. The walls of the structure are made in the basement part of natural stone with the transition to brickwork. Lintels above the doors and windows are wooden. Columns inside the building with a height of 6,890 mm are wooden. Bearing beams on columns are also made of wood. To determine the dynamic parameters of the structure and soil and its seismic stability, the mobile diagnostic complex "Struna-3MStrela" was used, including [2]:
• Three-component seismic vibration sensors - 5 pcs;
• Connecting cables - 5 pcs;
• Multi-channel analog-to-digital converter;
• A computer with a software package for analyzing seismic vibration signals. During the dynamic tests of the soil-structure system, micro seismic effects of the soil on the structure were recorded. The first sensor was installed at the base of the structure, the rest sensors were installed on the different heights in the building itself. The results of dynamic geophysical tests are shown in Figures 8-10.
The normative values of the periods of the natural oscillations of the structure were determined taking into account their spatial dimensions and the constructive scheme and amounted to:
[T1X ] = 0,14 sec ;
[T1Y ] = 0, 215 sec ;
[T1Z ] = 0, 3 sec ;
Spectral analysis of data obtained as a result of dynamic tests shows that the periods of natural oscillations of blocks in the first tone along the X, Y, Z axes have the following values:
T1X = 0, 24 s ;
T1Y = 0, 33 s ;
T1Z = 0, 26 s ;
The deficit of rigidity along the X, Y, and Z axes of the building was determined by comparing the calculated and experimental data:
The deficit of rigidity along the X, Y, and Z axes of the building was determined by comparing the calculated and experimental data:



A stiffness deficit along the X and Y axes was found, along the Z-axis there was no stiffness deficit.
The permissible value of acceleration or seismic stability was determined using the value of the period of natural oscillations obtained from the test results and the allowable roll or displacement value.
The maximum allowable displacement for the structure was determined by the following dependence:
Δd = i* h (4),
Where,
i: Maximum permissible roll;
h: Considered height of the object.
To calculate the value of the acceleration A through the displacement Δd, we apply the relation connecting the values of displacements, accelerations and periods:
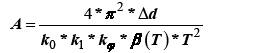 (5),
(5),
Where,
Δd: Maximum allowable values for the movement of the structure;
K0: coefficient that takes into account the peculiarity of the constructive decision and the degree of its responsibility K0 [3];
K1: Coefficient considering allowable damage k1 [3];
kϕ: Coefficient that takes into account the dissipative properties of the structure [3];
β(T): Coefficient of dynamism of the structure [3];
T: Experimentally obtained values of periods of natural oscillations of the structure.
The author on the basis of calculated-experimental data has established that when the stiffness is reduced by more than 30%, the seismic resistance significantly decreases.
Using the obtained dynamic parameters, the maximum permissible accelerations that could be sustained by the seismic action along the X, Y and Z axes were calculated (Table 3).
| № | Ах, m/s2 | Ау, m/s2 | Аz, m/s2 | Conclusion |
|---|---|---|---|---|
| 1 | 2,596 | 1,75 | 1,75 | Seismic resistance 1,75 m/s2 |
Table 3: Maximum acceleration in the axes that can withstand the construction.
Conclusion
According to the results of geophysical tests, the prevailing periods of natural oscillation of the soil base are in the interval 0.22÷0.45s.
Possible resonance phenomena the maximum acceleration of ground base oscillation is 0.24 g.
The structure has an earthquake resistance of at least 0.175 g.
Deficiency of seismic resistance is 0.065 g.
It is required to carry out engineering measures to seismically strengthen the structure. Thus, the proposed integrated technology for assessing the category of technical condition and seismic stability of historic structures can be used to diagnose and monitor structures, taking into account the dynamic impact on the construction of soils at their base.
References
- Grube GR, Kutschmar A, Romanik BV, Gegenwart BZ, Bildhandbuch E, et al. (2003) Designs from the Romanesque to the Present: A picture manual.
- Kirikov BA (1990) The oldest and newest seismic resistant structures. Moscow "Nauka".
- Paul CJ (1971) Engineering Flatures of the San Fernando Earthequake Fabrinary 9, 1971. California Institute of Technology, Pasdena California, pp: 174.
- Kirikov BA (1993) Selected pages of the history of seismic resistant construction. Moscow. Publisher Mir.
- Korobko VI, Korobko AV (2003) Control of quality of the building constructions: nhe vibro-acoustic technologes. Moscow 2003 Publishing House of the International Association Building Higher Educational Institute.
- Nigmetov GM, Chubakov M ZH (2011) Problemy monitoring buildings and structures, Seismic construction. Safety of buildings, p: 4.
- Code of rules. SP 14.13330.2014 Construction In Seismic Areas Of Snip Ii-7-81 Moscow 2016.
- Probability estimates of seismic loads on structures. Moscow "Science", 1987.
Citation: Nigmetov GM (2017) Assessment of the Category of Technical Condition and Seismic Stability of Historic Structures Using the Method of Dynamic Geophysical Tests. J Archit Eng Tech 6: 214. DOI: 10.4172/2168-9717.1000214
Copyright: © 2017 Nigmetov GM. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 2528
- [From(publication date): 0-2017 - Apr 21, 2025]
- Breakdown by view type
- HTML page views: 1774
- PDF downloads: 754










