Journal of Marine Science: Research & Development
Open Access

Wave spectra consists of both ‘wind-generated surface gravity waves which are the principal driving force of near shore fluid motions (e.g., long shore currents, rip currents, and undertow) and sediment transport (e.g., erosion and accretion of beaches, and the formation of bars and cusps); and infragravity waves. However, the incident waves and the nonlinearly excited higher frequency waves are predominantly dissipated in the surf zone while the nonlinearly excited lower frequency (infragravity) wave components reflect from the beach and often dominate wave run-up at the shoreline’ [1]. Therefore, wave swash oscillations patterns at the shoreline can be regarded as a signature of wave’s oscillations spectra in the surf zone.

Infragravity surface waves are generated by nonlinear interactions of gravity /wind wave or swells and have periods which ranged from 20 to200s. Also, it can be tidally-modulated as observed in the inner shelf and in the regional seismic record which could contribute to the Earth’s background free oscillations. Rhie and Romanowiez [2] Dolence and Romanowiez [3], Tanimoto [4], Webb [5] and Rabinovich posited infragravity waves as waves types with periods ranging from 25-30s to 300-600s, frequencies between 0.003 and 0.004Hz, and wavelengths between 100m and 10km. They occur both in the deep and coastal oceans [6-8] and are observed to be stronger near the shoreline [9], where tidal variations of surf zone width, beach slope and profile might affect the generation, energy dissipation, reflection or refraction.

Moreover ‘Infragravity waves are surface gravity waves with frequencies ranging from 0.004 to 0.04Hz [10] and a few mm to cmhigh in the deep ocean [11-13] but can exceed 1:0m close to shore under storm conditions [14-15]’ cited in Bertin et al. 2020 [16]. Infragravity waves induce cells circulations through generation of long shore and cross-shore currents, and transport sediment on the shoreline and surf zone [17-18].

When infragravity waves break at the shorelines; varying degrees of sediment perturbations and transport by cross-shore and long shore currents initiated by the breaking waves occur. These cause sediment perturbation and transport on the beach which result in erosion and accretion with morphological adjustment of the beach into beach cusps, log-spiral crenulated, embayment and intertidal bars, etc., [19].

Shoreline erosion is a global problem attributable to impact of waves on the shoreline. The dynamics of shoreline erosion reveals that accretion processes occur simultaneously with rosin but the net volumetric change of sediment transport into and out of littoral cells on the shoreline defines the morpho-dynamic status of the shoreline [20]. The net product of shoreline morph dynamics in recent past along Nigerian coastline is shoreline erosion which resulted in shoreline retreat. This can be attributed to changes in atmospheric and ocean dynamics such as global sea level rise and climate change [21-24]. These phenomena increased hydrodynamic processes to the extreme, such as storm surges with the attendant negative impact on the shoreline which include shoreline erosion, coastal submergence, threat to integrity of coastal structures and installations, etc. Previous works on coastal erosion along Nigerian coastline by several authors have indicated that shoreline erosion is caused by the actions of wave swash and backwash and long shore current transports on beaches [25-28]. Therefore, the need to investigate on the fundamental components of the wave spectra which are considered as the principal agents of shoreline changes is imperative. So, the focus of this study is to analyze short -term wavespectra and its effect on shoreline changes as well as implications for coastal engineering projects on the strand coastal plain of Ibeno beach, east of Qua-Iboe River estuary, Southeastern coast of Nigeria.

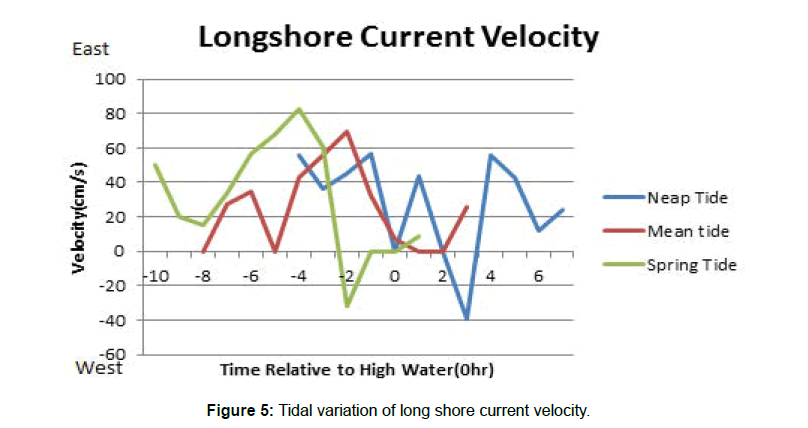
The downdraft shoreline adjoining Qua-Iboe River Estuary is located in Ibeno Local Government Area of Akwa Ibom State, Southeastern coast of Nigeria (Figure 1). The shoreline is a mesotidal tropical sandy beach exposed to semi-diurnal tides and southwesterly waves with amplitude less than 20cm, which is associated with southwesterly wind conditions which vary annually from calm (November- February) through transitional (February-April) and storm ( May- October) [29]. Modal wave periods close to the shore are 8-12s. Long shore current velocities along the ocean shoreline ranged 50-125cm/s east with periodic reversals to the west at the downdraft beach contiguous to the estuary mouth due to changes in tidal stage. The shoreline represents an exposed section of the abandoned beach ridges laterally bounded by mangrove swamps of the lower Deltaic Plain of Holocene age. It is underlain by Sombreiro-Warri Deltaic Plain sand of late Pleistocene [30]. The beach is texturally homogeneous with predominantly well sorted fined-grained sand [31].

Figure 1: Google map of the study area showing monitoring station [X].

The study covered a period of seven days from August 24 (neap tide) through 30 (spring tide) in 2015. The monitoring station for this study was established at location (X) defined by Longitude 70 591.4011 E and Latitude 40 321 3011 N, 500m away from Qua Iboe River estuary mouth (Figure 1). Wave swash oscillations times were recorded for each successive wave swash as it hits each of a series of range poles strategically fixed at 10m spacing intervals across the beach foreshore for a 12- hourly tidal cycle. Each recorded time was subtracted from the preceding one to obtain the wave swash period. The above method is an improvised technique inspired from previous work such as Hollman and Guza [32]. The wave swash frequencies and periods were grouped into 10-class intervals and their spectral percentage frequencies determined per hour over a 12- hour tidal cycle. Spectral Energy Index (SEI) was computed as an inverse of spectral percentage frequencies. Swash lengths were estimated based on the length of the beach foreshore relative to the range poles as the distance of the wave swash from the breaking point to the end of the swash length at every fifteen (15) minutes. Other hydrodynamic parameters such as wave-breaker height and water depth were measured, along the ocean shoreline, with the aid of a graduated staff. It was measured by placing the tip of the graduated staff on the water surface as the wave advanced to the beach and read off the height of the crest at breaking. The corresponding water depth was also measured immediately after the wave has broken by placing the tip of the staff to the bottom of the surf zone at the wave breaker point. Long shore current velocities were also monitored at quarter -hourly intervals as a time taken by a buoyant object to freely drift over a known distance. Daily beach profiles were made at the station over a near-spring tidal phase, while linear beach profile measurements were converted to beach volumetric change within a one-meter wide transect. At the monitoring station geomorphic beach segments were demarcated into: backshore, upper-, mid- and lower foreshore.

Wave parameters

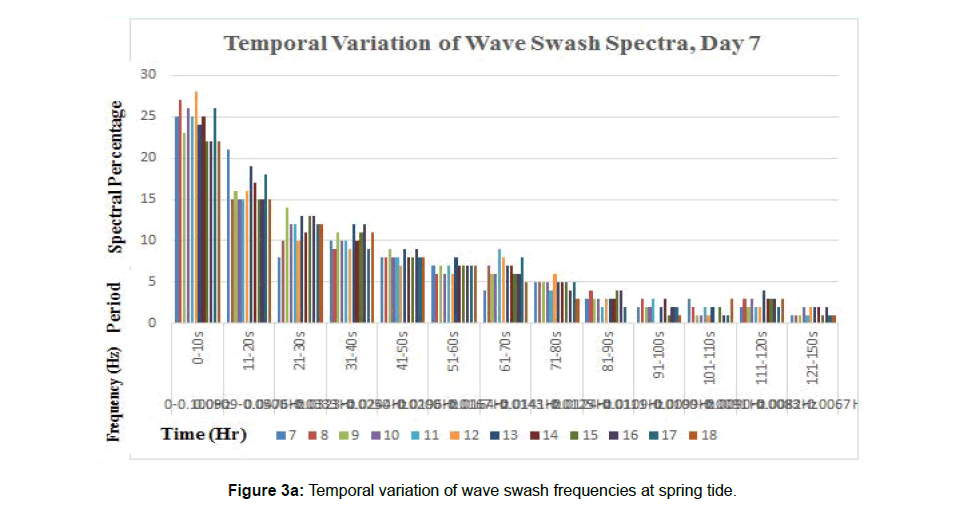
Result of wave swash spectra occurrence frequencies within a period class of 10s per hour in Figures 2a and 3a reveals that gravity and infra-gravity wave’s oscillations frequencies are inversely related with the spectral percentage frequencies of occurrences irrespective of tidal stage. However, analysis of the wave swash spectra filtered within a period class of 30s transformed into corresponding frequency intervals per hour in Figures 2b and 3b also reveals that gravity wave frequencies ranged between 0 and 0.033Hz while infragravity wave frequencies ranged from 0.0322 to 0.0067Hz and depicted five harmonic waves frequencies spectra at the coastal plain. The wave swash spectral frequencies within the period class defined later, and based on the order of arrival of the wave swash at the shoreline, are denoted as First Harmonic (0.0082-0.0067Hz), Second Harmonic (0.0110-0.0083Hz), Third Harmonic (0.0164-0.0111Hz) and Fourth Harmonic ( 0.0322- 0.0166 Hz) Waves frequencies respectively in the infragravity wave spectrum; while gravity waves frequencies (0-0.0333Hz) spectrum is the Fifth Harmonic Waves frequencies group and the last to arrive the shoreline.

Figure 2a: Temporal variation of wave swash frequencies at neap tide.

Figure 2b: Analysis of wave swash spectra on neap tide.

Figure 2c: Analysis of Spectral Energy Index at neap tide.

Figure 3a: Temporal variation of wave swash frequencies at spring tide.

Figure 3b: Analysis of wave swash spectra at spring tide.

Figure 3c: Analysis of Spectral Energy Index at spring tide.

In Figures 2b and 3b, the percentage occurrences of gravity waves (fifth harmonic frequencies) per hour, during flood and ebb stages, fluctuated around fifty percent (50%) and the apexes of the wave frequency bands showed a sinusoidal waveform. At neap tide, in Figure 1b, high water was recorded at the eleventh hour while at spring tide, in Figure 3b, Low water was also recorded at the eleventh hour. Also noted from the two plots are the occurrences of three wave crests and troughs in the waveforms over a twelve-hour tidal cycle with somewhat irregular periodicities respectively. The waveforms of the gravity waves spectrum in Figures 2b and 3b may be considered as a signature of southwesterly swell waves motions in the Gulf of Guinea towards the shoreline. But the irregular periodicity in the occurrences of the wave crests and troughs in the waveforms may be attributed to effects of increase in gravitational force in the Sun- Earth- Moon system, phase lag, shoaling, refraction, wave-waves interactions in the dissipative surf zone, etc., during phase change from neap to spring tide.

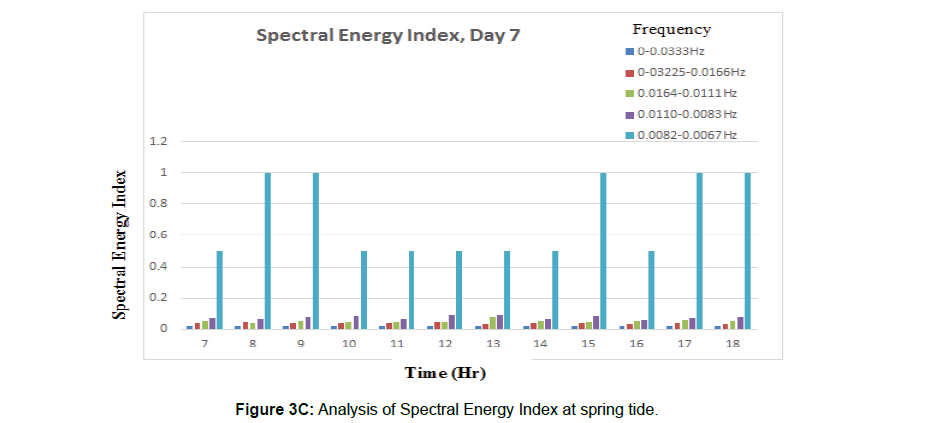
In the infragravity wave spectrum, at neap tide, with exception at high water in which the fourth harmonic wave frequencies were the highest, the third harmonic wave frequencies recorded the highest spectral percentage occurrences within a range from 25 to 30% per hour followed by the fourth, the second and the first wave harmonic frequencies in the order of percentage decrease during the twelve-hour tidal cycle. Whereas, at spring tide, the fourth harmonic wave spectral frequency percentages have the highest percentage concurrences and fluctuated almost within the range of 25 to 30% per hour while the percentage of occurrences of the third, second and the first harmonic wave spectral frequencies decreased in the same order. However, in Figures 2c and 3c, the Spectral Energy Indices (SEI) increased from the Fifth Harmonic wave spectrum ( 0.01-0.02), through the Fourth Harmonic Wave Spectrum (0.03 -0.05), the Third Harmonic Wave Spectrum (0.03-0.07), the Second Harmonic Waves Spectrum (0.04- 0.09) to the First Harmonic Wave Spectrum (0.5-1.0) which has the highest energy level in the wave spectra.

Obviously, from the above analysis of wave swash oscillations, the wave spectra in the study site is dominated by gravity waves (52.28%) over infragravity waves (47.72%) which corroborates the classification of ocean wave spectra according by Munk; and is also consistent within the range of classifications of infra-gravity waves by Longuet-Higgins and Stewart [33], Herbers et al. [34], Okihiro and Guza [35,36] and Rabinovich. Significantly, the percentage occurrences of the first harmonic wave frequencies (0.0082-0.0067Hz) in the infragravity wave spectrum were the least and fluctuated within the range from 1 to 2% per hour but have the highest Spectral Energy Indices (0.5-1.0).

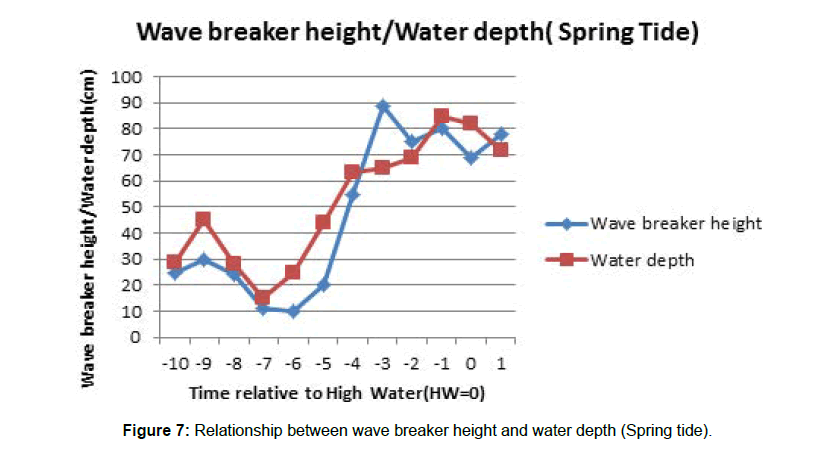
Furthermore, other wave-breaker parameters recorded during the study period reflected the dissipative characteristics of the surf zone. These include wave- breaker height and water depth which increased from 10cm at low tide to a maximum value of 80cm at high water during neap and spring tides (Figures 4-7). Wave swash length varies from 5to10m at low tide and from 50 to7om at high tide and was strongly influenced by increase in wave- breaker height and water depth and the gentle beach foreshore slope which ranged between 2 and 40. By implication, infragravity waves breaker heights increased with rising tide from low to high tide and from neap to spring tide. The percentage occurrence of spilling wave breakers was 60% over 40% of plunging breakers.

Figure 4: Tidal variation of wave breaker height.

Figure 5: Tidal variation of long shore current velocity.

Figure 6: Relationship between wave breaker height and water depth (Neap tide).

Figure 7: Relationship between wave breaker height and water depth (Spring tide).

Effects of wave spectra on the shoreline

Effects of wave swash oscillations at the shoreline are numerous but for the purpose of this investigation, the discussion below is made in respect of short- term wave dynamics and shoreline changes.

Wave dynamics

Effects of wave actions in the study area are examined based on five harmonic wave’s frequencies spectra, dominant wave processes and short-term shoreline changes. This discussion is based on both in-situ virtual observations and result of empirical data acquired during the investigation.

First harmonic infragravity waves frequencies spectrum (0.0082-0.0067Hz): This group of infra-gravity waves is the first to arrive, advance, inundate, and impact the beach in every 2 to 3 minutes interval. The First Harmonic Infragravity Waves spectrum has the lowest spectral percentage frequency of occurrence (3.20%) and the highest Spectral Energy Index in the wave spectra, characterized by highest wave- breaker height and water depth, generated the longest wave swash, backwash and undertow of about (70m) in lengths. In addition, the wave frequency band generates highest long shore currents velocities, scour and trigger-off cross-shore sediment movement on the beach at the highest degree and increase rip currents energetics than other harmonic wave’s frequencies spectra. However, the wave’s frequencies spectrum has the propensity to propel, with the highest force, energized by maximum wave-breaker height and water depth at a time (Figures 3a and b), any floating object in the surf zone to the shoreline than other harmonic wave’s frequencies. Therefore, the energy radiation and transmission by the First Harmonic Infragravity waves at the shoreline could be a factor for seiches and harbor oscillations which affect anchorage and moorings of marine vessels and other facilities in marinas. Knowledge of the above energy level is essential in engineering designs of coastal structures such as jetties, groins, seawalls, etc.

Second harmonic infragravity waves frequencies spectrum (0.0110-0.0083Hz): This harmonic is the second group of infragravity waves with 7.51% spectral frequency percentage of occurrence to impact the shoreline. Wave swash and backwash of these waves group performs an intermediary and a transitory role in effect between the First and the Third harmonic Infragravity Waves Groups. These include superposition and wedging of backwash and undertow from the impact of the First Harmonic Infragravity Waves causing intermittent erosion on the beach. Precisely, this wave frequency spectrum modulates the roles of the First Harmonic Waves Frequencies spectrum.

Third harmonic infragravity waves frequencies spectrum (0.0164-0.0111Hz): This wave spectrum is the third infra-gravity waves frequencies group with 12.33% frequency of occurrence to inundate the shoreline. It superposes on waves swash and backwash of the First and Second Harmonic Infragravity Waves and disperses sediment in the area. The wave swash processes of the Third Harmonic Infragravity Waves transport distribute and spread sediment on the beach by the processes of long shore and cross-shore currents. It performs a translational role between the Second and the Fourth Waves frequencies spectra.

Fourth harmonic infragravity waves frequencies spectrum (0.03225-0.0166 Hz): This group of infra-gravity waves with 24.68% spectral frequency percentage of occurrence is the fourth to impact the beach and the lowest frequencies in the infragravity waves spectrum. Similar to the Third Harmonic, wave swash and backwash actions of the Fourth Harmonic Infragravity Waves perform an intermediary and transitory role in sediment transport between the Third Harmonic wave’s frequencies (infragravity waves) and Fifth Harmonic waves (gravity waves) Frequencies Spectra.

Fifth harmonic gravity wave frequencies spectrum (0-0.0333Hz): The gravity waves, with 52.28% frequency of occurrence in the wave spectra, at breaking with the associated wave swash processes, sort, winnow and rework fine sediment into suspension. This wave spectrum, with it typical oscillatory and turbulent motions and mixing processes at the highest degree in the surf zone, performs the role of a compactor machine on the surface sediment. The above analysis suggests that incident waves groups of first, second, third, fourth and fifth harmonic waves frequencies oscillations waves spectra, inundate the beach at every 2 to 3 minutes interval during flood and ebb tides.

Shoreline morphodynamics

In Figure 8, net sedimentation patterns at the monitoring station fluctuated between -1.32m3 and -3.51m3 at neap and spring tides respectively indicative of erosion as shown by the concave beach profile plots. The First Harmonic Infragravity Waves were observed in-situ as the principal agent of cross-shore transport of sediment at the beach while the Second Harmonic Infragravity Waves in union with backwash from the First Harmonic waves generate long shore sediment transport. The net product of sediment transport between wave swash and backwash actions determines the morpho-dynamic state of the beach either as erosion or accretion. The erosion potential of the first harmonic waves spectrum, were observed in the field and noted from the beach profile plot (Figure 8) to increase with change in phase from neap to spring tide. In summary, the First Harmonic Infragravity Waves oscillations spectrum at breaking, dissipates energy (SEI, 0.5-1.0) and performs the task of a pay loader heavy equipment machine on the shoreline. It causes erosion, uproots trees, demolishes shoreline protection and stabilization structures, etc., during storm weather and transports sediment to the beach from the surf zone during calm weather conditions respectively. Intuitively, from the above analysis, the First and Second Harmonics Infragravity Waves Frequencies Spectra, during calm weather condition, will become the principal agents of sediment deposition at the shoreline while erosion will be the case in stormy weather condition. The wave swash actions of the Third Harmonic Infragravity Waves Frequencies Spectrum spreads sedimentary materials at the beach foreshore like motor grader heavy equipment machines in the direction of long shore and cross-shore currents transports accordingly. The Fourth Harmonic Infragravity Waves and Fifth Harmonic Wave Frequencies Spectra (gravity waves) winnow, sort, mix and rework fine sediment into suspension while coarser fractions settle at the bottom. The oscillatory and turbulent motions of gravity waves, act on sediment surface like a compactor heavy equipment machine.

Figure 8: Daily beach profile at the monitoring station.

The First and Second harmonic groups of infragravity waves oscillations spectra, which have the highest spectral energy indices than other harmonics, have been identified and delineated in the course of this study as the principal agents of erosion/accretion at the shoreline and the main factors in harbor oscillations and rip currents dynamics. However, an understanding of energy radiation and transmission by different harmonic infragravity waves frequencies spectra at the shoreline is crucial for engineering applications and designs of coastal structures, such as harbors, marinas, seaports, sea walls, breakwaters, etc.; and sustainable protection and management of shoreline erosion in the coastal zone. Moreover, infragravity waves have strong implications on near shore coastal sediment transport and self-cleansing potential of the surf zone than gravity waves, while gravity waves have a higher mixing and modulation potentials in the wave spectra than infragravity waves. On the other hand, the accretion/ construction and/or destruction/erosion dynamics and functions of different wave frequency bands, in the wave spectra, on the shoreline morphodynamics as discussed earlier, can be likened to the role of different heavy equipment machines used by construction companies (eg. Pay loader, Motor grader, Compactor, etc.). To construct roads or demolish structures and uproot trees.

This research did not receive any grant from funding agencies in the public, commercial, or not-for-profit sectors. The assistance of the following personnel in the field: Gabriel Udo-Akuaibit, Uduak Akpan and Ndifreke Gabriel are highly appreciated.