Research Article Open Access
A Derivative-less Approach for Generating Phase Envelopes
Siddiqui F*
Research Scientist, Petroleum Engineering, Texas Tech University, 2500 Broadway, Lubbock, TX 79409, USA
- *Corresponding Author:
- Siddiqui F
Research Scientist, Department of Fluid Flow
Texas Tech University, 2500 Broadway, Lubbock, TX 79409, USA
Tel: 8062812458
E-mail: fahdsiddiqui@gmail.com
Received date: October 21, 2015; Accepted date: November 17, 2015; Published date: November 21, 2015
Citation: Siddiqui F (2015) A Derivative-less Approach for Generating Phase Envelopes. Oil Gas Res 1:106. doi: 10.4172/2472-0518.1000106
Copyright: © 2015 Siddiqui F. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Oil & Gas Research
Abstract
Petroleum engineers are often interested in the phase envelope that describes the characteristics of the pore fluids. These phase envelopes are normally generated by conducting laboratory measurements involving expensive PVT equipment and trained personnel. By using an Equation of State (EOS) based computer model that requires some hydrocarbon composition data, these envelopes can be generated almost instantly. An algorithm for generating a complete phase envelope using computer modeling was proposed by Michelsen. His procedure, based on EOS modeling, may sometimes suffer from convergence issues, especially near the critical region. In addition, his procedure requires the partial derivatives of fugacity, which are often difficult to get. In this work a phase behavior model was developed that incorporates some modifications to Michelsen’s algorithm avoiding the need for calculating these derivatives, which in turn put fewer requirements on the data and computation. These modifications allowed running the model successfully for different hydrocarbon systems without any convergence issues. Because the new model does not have to deal with the partial derivatives of fugacity, it can work with any EOS based phase behavior model. The new method has been applied to three different reservoir fluids and shows an exact match with the phase envelope generated using commercial software.
Keywords
Phase envelopes; Fugacities; Interpolating polynomial; Dew point
Abbreviations
EOS: Equation of state; PR: Peng-Robinson; SRK: Soave-Redlich-Kwong
Nomenclature
f : Mole fraction
K: Equilibrium Ratio
z: overall composition in mole fraction
Subscripts
i: Component
v: Vapor
Introduction
Phase envelopes can be generated, in principle by performing a series of saturation pressure calculations at specified temperatures. But this method is not recommended as it is time consuming and is susceptible to convergence problems at higher pressure and temperature conditions. Michelsen [1] proposed a procedure for phase envelope generation by first starting the calculation at moderate pressure/temperature conditions and then using the K-values, and fugacities of previous saturation points to estimate the next saturation point. This procedure ensures a reasonable initial estimate and creates no problems when the data passes through the critical point. However, Michelsen uses the Newton-Raphson technique for solving the non-linear equation to calculate successive saturation points. His method is robust and allows a rapid construction of the phase envelope. Because his method is based on the Newton-Raphson method, it requires the first partial derivatives of the component fugacities with respect to pressure and temperature to populate a Jacobian matrix.
Calculation of the first partial derivatives of the component fugacities may not be practical to obtain analytically for some EOS that have complicated equations for fugacities. Therefore, numerical techniques, such as the finite difference method, are often used to obtain the first partial derivatives of the component fugacities.
Most of the convergence issues arise from selecting the initial K-values that are not within the radius of convergence of the numerical method being used. It is therefore, of paramount importance that the K-values be initialized correctly especially in the critical region. Michelsen uses the interpolating polynomials to estimate the K-values for the next points.
Proposed Modifications
Two phase flash algorithm using an EOS: Generally the nonlinear Muskat-McDowell [2] equation is solved using the Newton- Raphson method but the Newton-Raphson method may often diverge from the correct solution.
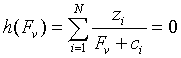 (1)
(1)
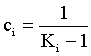 (2)
(2)
The Newton-Armijo method can be used to solve the Muskat- McDowell equation in a reliable method. The code for two-phase flash calculations in this study was developed using the Newton-Armijo method. The flash procedure can be used to find: liquid and vapor phase Z-factors, fugacities, molar compositions, and K-values and mole fraction vapor/liquid.
Phase envelope generation procedure: This paper proposes the following modifications to the phase envelope generation procedure described by Michelsen. These modifications make the original procedure more robust and provide an alternate way of solving the non-linear problem in simpler terms.
K-value initialization: The K-values are initialized by Wilson’s [3] method only at the initial point of the phase envelope. Since this is done at a moderate pressure and temperature, it guarantees convergence [1]. Each successive calculation uses K-values extrapolated using the PWCH (Piece-Wise Cubin Hermite) interpolating polynomials with the flash calculation performed at preceding Pressures and Temperatures. This ensures convergence.
Initializing the EOS flash calculations this way avoids all convergence-related problems with a few rare exceptions. In the case of such an event the Pressure and Temperature steps can be reduced and the calculations can be repeated.
Bisection method: The bisection root finding method is used to find the saturation points. This does not require the first partial derivatives of fugacity and this method is used in place of the multidimensional variant of the Newton Raphson Method, which relies on forming a Jacobian of first partial derivatives of fugacity with respect to temperature, pressure and composition.
The desirable property of the Newton-Raphson method is its ability to converge to a solution quadratically. This essentially means that it should take up to four iterations to converge to a solution on a doubleprecision floating point machine when starting from a guess that is accurate up to 1 decimal place. However, the property of quadratic convergence is only realized in certain cases where the initial guess is really close to the root (within the radius of convergence). Beyond the radius of convergence, the Newton-Raphson method falls back to linear convergence and may fail to converge in some cases. Since the bisection method converges linearly to the solution, it will take up to 16 iterations to converge on a double-precision floating point machine, starting from a guess value accurate up to 1 decimal place. Although it will be significantly slower, the bisection method is failsafe and always converges to the solution [4]. Additionally the bisection method does not require the partial derivatives of fugacity. Hence it is easier to program the codes and in some instances the bisection method works as good as the Newton-Raphson method in terms of number of computations since the derivatives are not being calculated at each iteration level [4].
Interpolating polynomials: Another modification done in this study is the use of interpolating polynomials in which the results of the previous saturation point calculations are used to find an interpolating polynomial. This polynomial is then used to extrapolate over a small pressure or temperature range, to estimate the next saturation point and also the K-values at this point. This new saturation point and K-values are then used to initialize the bisection calculation, which converges much quickly because it is closer to the actual solution.
Modified algorithm
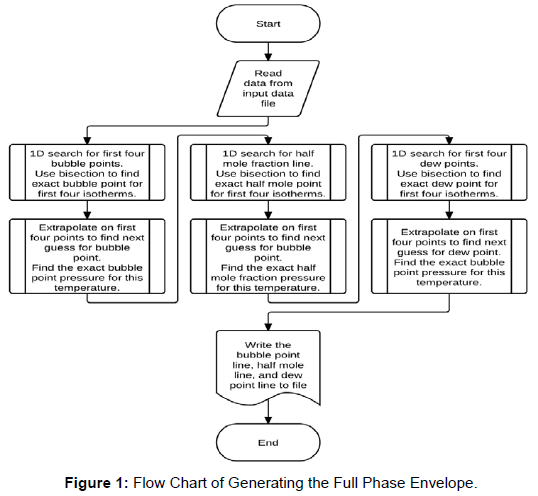
Bubble point line calculation: Run the EOS flash calculations on increasing pressures steps at an isotherm and look for a sign change on mole fraction vapor. Run PWCH interpolation to find an estimate of saturation pressure. Run the bisection root finding method on this estimate to find the exact Saturation Pressure for this temperature.
Then on the next isotherm start from this pressure and keep increasing the pressure until maximum specified pressure is reached. Use interpolation, followed by bisection, to find the next bubble point pressure at the next isotherm. Continue for two more steps like this, while using the K-values from previous pressure temperature conditions to initialize the EOS flash calculation to ensure convergence.
To accelerate calculation speed, these four points can be used to extrapolate the saturation pressure along with its K-values for the next isotherm. In this way, the use of brute force searching for sign change can be avoided all together. Use bisection root finding method on this extrapolated bubble point pressure to find an exact bubble point pressure within the specified tolerance.
This acceleration leads to quicker calculation of bubble point calculation and no problems are encountered while passing through the critical point. The procedure is repeated until the root finding subroutine fails, which only happens when the temperature exceeds the cricondenthem; i.e. only a vapor phase is encountered everywhere on the isotherm (Figure 1).
Dew point line calculation: The dew point line calculation can be done similar to bubble point line calculation. Only this time the temperature is reduced instead of increasing it. This is because the initial calculations are done farther away from the critical point to ensure convergence. Similarly run the EOS flash calculations on a number of different pressures at an isotherm (maximum specified temperature) and look for a sign change on mole fraction liquid. Run PWCH interpolation to find an estimate of dew point pressure. Run the bisection root finding method on this estimate to find the actual dew point pressure at this temperature.
Then on the next (lower) isotherm start from this pressure and keep increasing the pressure until maximum specified pressure is reached. Use interpolation followed by bisection to find the next bubble point pressure at this next isotherm. Continue for two more temperature steps like this while using the K-values from previous pressure and temperature conditions to initialize the EOS flash calculation to ensure convergence.
To accelerate the calculation speed, these four points can be used to extrapolate the dew point pressure along with its K-values for the next (lower) isotherm. In this way, the use of brute force searching for sign change can be avoided altogether. Use bisection root finding method on this extrapolated dew point pressure to find the exact dew point pressure within the specified tolerance.
Half mole fraction vapor and other quality lines: Similarly the procedure can be repeated for looking for a sign change on mole fraction liquid less one half to generate the half-mole-fraction-vapor quality line and other quality lines.
Advantages of modified phase envelope algorithm: No partial derivatives requirement is placed on fugacity with respect to Pressure, Temeprature, K-values etc. This in turn means that any EOS can be used with this algorithm without knowing the partial derivatives of fugacity. This is useful because of some disadvantages of the Newton- Raphson method which may be encountered in rare cases. These rare cases can be realized during the EOS calculations at high pressures and especially near the critical point where the Newton-Raphson method struggles with convergence. Moreover, the Newton-Raphson method may not be applicable if obtaining the derivatives of fugacity is difficult or cumbersome.
Following disadvantages of Newton’s method prompted the use of Bisection method for the phase envelope generation calculations:
1. Requirement of direct evaluation of derivatives. The derivatives may be obtained numerically which reduces the Newton’s method to the Secant method which has the same convergence rate as Bisection method. Because the real power of Newton’s method lies with the “Quadratic convergence rate” associated with it, reducing it to the secant method only gives a linear convergence rate and therefore, loses its advantage over the Bisection method.
2. Initial guess not close to root: If the initial guess is not in the radius of convergence for the Newton-Raphson method, the method may fail.
3. Stationary point: If the stationary point of the function is encountered, the method will terminate due to division by zero. This will happen because the function derivative is zero causing the Newton’s method to blow. This can also happen if the derivative is close to zero.
4. Overshoot: If the first derivative is not well behaved in the vicinity of the root, the method may overshoot and diverge to infinity.
The Bisection method does not suffer the disadvantages associated with derivatives and is simpler and robust. In fact a black-box EOS can be programed to run with this algorithm and the only requirement from the EOS would be mole fraction vapor (or liquid) at specified pressure and temperature conditions and no requirement of fugacity or partial derivatives of fugacity is placed on the EOS. This algorithm can also provide initializing K-values to the black-box EOS to aid in convergence of flash calculation and also an overall acceleration of computation because extrapolated K-values will be closer to the actual K-values (or K-values initialized by Wilson equation).
Validation of the proposed algorithm: The phase envelope generation was verified against commercial software by commercial software which uses the Michelsen’s algorithm to generate the phase envelope. Phase envelopes were generated using the commercial software and the modified algorithm on three real field datasets. These datasets include:
1. A light oil sample
2. A rich gas condensate
3. A lean gas condensate
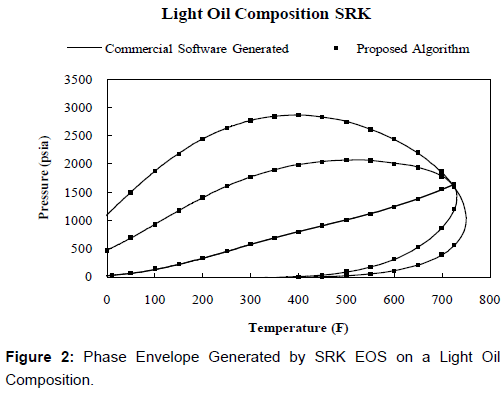
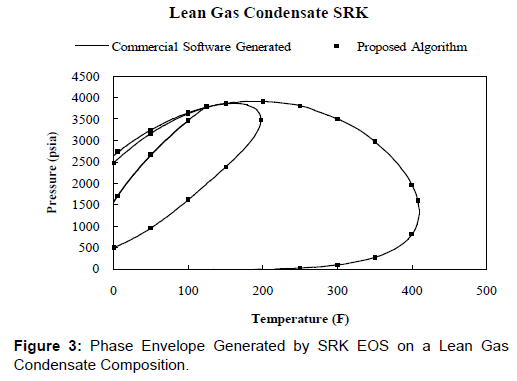
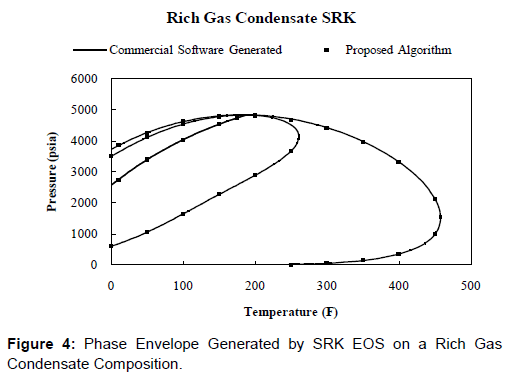
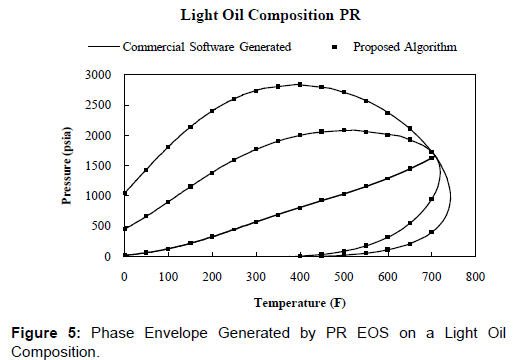
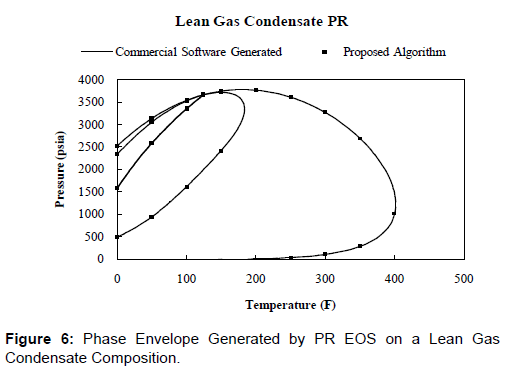
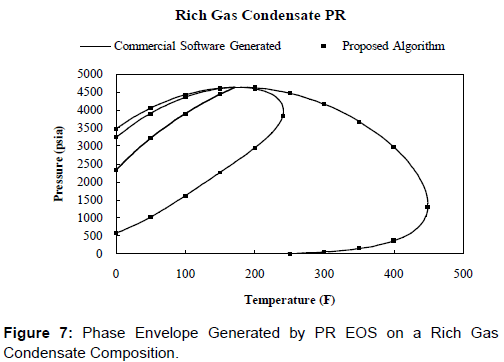
Figures 2-7 show a comparison of the results from the derivativefewer algorithms proposed in this paper and the phase envelope generated using the commercial software. The results match exactly, validating the proposed algorithm. Figures 2-7 show that the phase envelopes generated using the proposed algorithm and the commercial software are superimposed. This is expected since both are generated using the same EOS on respective datasets. If the results were not superimposed, that would suggest a problem with the algorithm. The proposed algorithm mimics exactly the phase envelope generated using Michelsen’s algorithm while incorporating a derivative-less technique and predicts the exact same results.
Figures 2 and 5 show the phase envelopes of a light oil composition (Table 1). Figure 2 was generated using the SRK [5] equation of state using commercial software and the algorithm presented in this thesis. The results superimpose on top of each other, validating the algorithm. Figure 5 was generated using the PR [6] equation of state, and it shows a comparison which also resulted in an exact match against commercial software, also validating the algorithm presented in this report.
| Composition | Mole Percent (%) |
|---|---|
| N2 | 0.16 |
| CO2 | 0.91 |
| H2S | 0 |
| C1 | 36.47 |
| C2 | 9.67 |
| C3 | 6.95 |
| iC4 | 1.44 |
| nC4 | 3.93 |
| iC5 | 1.44 |
| nC5 | 1.41 |
| C6 | 4.33 |
| C7+ | 33.29 |
C7+ Properties:
Molecular Weight: 218
Specific gravity: 0.8515
Bubble Point Pressure of Oil at 220F = 2620psia (Used for matching)
Table 1: Light Oil Composition Used for Phase Envelope Calculations.
Figures 3 and 6 show the phase envelopes of a Lean Gas Condensate fluid system (Table 2). Figure 3 was generated using the SRK EOS and again it shows an exact match against commercial softwre. The quality lines also match up properly suggesting that the algorithm is working properly. Similarly for Figure 6, which was generated using the PR EOS, the results are an exact match.
| Composition | Mole Percent (%) |
|---|---|
| N2 | 0.47 |
| CO2 | 2.42 |
| H2S | 0 |
| C1 | 68.22 |
| C2 | 11.8 |
| C3 | 5.46 |
| iC4 | 0.83 |
| nC4 | 1.74 |
| iC5 | 0.72 |
| nC5 | 0.74 |
| C6 | 1.07 |
| C7+ | 6.53 |
C7+ Properties:
Molecular Weight: 148
Specific gravity: 0.793
Dew Point Pressure at 275F = 4521psia (Used for matching)
Table 2: Lean Gas Condensate Composition Used for Phase Envelope Calculations.
Figures 4 and 7 show the phase envelopes of a rich gas condensate system (Table 3). Figure 4 was generated using the SRK EOS, while the Figure 7 was generated using the PR EOS. The comparison against their respective commercial software generated plots is an exact match and no deviation is noticed anywhere on the phase envelope. This sufficiently verifies the proposed algorithm.
| Composition | Mole Percent (%) |
|---|---|
| N2 | 1.35 |
| CO2 | 0.4 |
| H2S | 0 |
| C1 | 72.69 |
| C2 | 7.84 |
| C3 | 3.85 |
| iC4 | 1.04 |
| nC4 | 1.63 |
| iC5 | 0.7 |
| nC5 | 0.78 |
| C6 | 1.59 |
| C7+ | 8.13 |
C7+ Properties:
Molecular Weight: 148
Specific gravity: 0.793
Dew Point Pressure at 225F = 4800psia (Used for matching)
Table 3: Rich Gas Condensate Composition Used for Phase Envelope Calculations.
The above results showed that for the three completely different fluids used to generate the phase envelopes, an exact match of the dew point line, bubble point line and on the quality lines can be obtained using the proposed method. This verifies the algorithm against Michelsen’s algorithm for PR EOS and SRK EOS.
Uncertainty analysis: The described algorithm solves the optimization problem without derivatives. It depends on the Equation of State being used, but more importantly it depends on the quality of input data. This is also true if any other algorithm is used to solve this problem, such as any commercial software.
Mathematical Solution Techniques
Newton-Raphson method
Also known as the Newton’s method, this method is used for solving f(x) = 0. For the one variable case we start with an initial guess x0 and iterate to find the next value using the following equation.
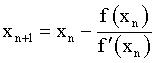 (3)
(3)
This consideration can also be extended to the case of more than one variable. It has the desirable property of converging to a solution quadratically.
This method requires the function to be continuously differentiable [4] and also note that if at any iteration the first differential, f’(xn) = 0 this method will terminate. Moreover in many instances, it if the first derivative of the function is close to zero near the root, this method will diverge [4]. Table 4 shows such an example where Newton-Raphson method fails. Further disadvantages of this method are discussed in subsequent sections of this thesis where the practical application of this method is considered for flash calculations and phase envelope generation.
| n | xn | |xn-xn+1| | f(xn) |
|---|---|---|---|
| 0 | 2 | - | 1.107 |
| 1 | -3.535 | 1.107 | -1.295 |
| 2 | 13.951 | 5.536 | 1.499 |
| 3 | -279.344 | 293.295 | -1.567 |
Table 4: Newton-Raphson Method for solving f(x) = tan-1(x).
Newton-Armijo method
Since Newton’s method may fail for a bad initial guess, the method may blow up due to division by small numbers. For example in the case of f (x) = tan−1(x) when given a sufficiently large starting value x0 = 2 (Figure 8).
Subsequent iterations blow up, reaching xn = 1021 in seven iterations. The increase in | xn+1 - xn | is not necessarily the evidence of failure although it does indicate that the region of quadratic convergence has not yet been reached. But the increase in successive values of | f(xn) | suggests a problem.
The backtracking idea is to reduce the Newton step as needed to avoid catastrophic overshoot. The Armijo backtracking algorithm can be simplified as:
1. Start at a current iterate xn, and evaluate fn = f(xn) and sn = -fn/ f’(xn). Initialize t = 1.
2. Compute a trial step yn,t = xn + tsn.
3. Compute f (yn,t).
4. If |f (yn,t)| < β |f(xn)| for some specified β =1, then accept the step. Set xn+1 = yn,t. Check for convergence: if converged, stop; otherwise, return to step 1.
5. Decrease t and return to step 2. The most common step reduction is to reduce t by a factor of 2.
The Newton-Armijo method attempts to compensate for a poor initial guess by backing off from a full Newton step when it does not reduce the residual. This method serves as a modification to Newton’s method with backtracking regulated by Armijo condition; hence it is often called Newton-Armijo method. It has the advantage of falling back, essentially, to bisection in case the Newton step begins to blow up. This is desirable for functions that tend to cause convergence issues like the example stated above of f(x) = tan-1(x).
Bisection method
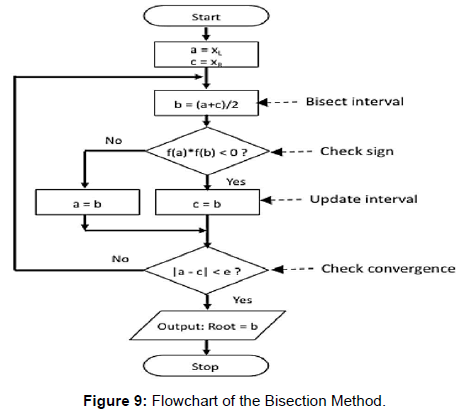
This method works by first finding the interval containing the root by looking for a sign change. At each step the method divides the interval into two by computing the midpoint c = (a+b)/2 of the interval and the value of the function f(c) at that point. Unless c is itself a root (which is very unlikely, but possible) there are now two possibilities: either f(a) and f(c) have opposite signs and bracket a root, or f(c) and f(b) have opposite signs and bracket a root. The method selects the subinterval that is a bracket as a new interval to be used in the next step. In this way the interval that contains a zero of f is reduced by half at each step. This process is continued until the interval becomes sufficiently small (Figure 9).
The method is guaranteed to converge to a root of f if f is a continuous function on the interval [a, b] and f(a) and f(b) have opposite signs. The absolute error is halved at each step so the method converges linearly, which is slower than the Newton’s Method.
SI Metric Conversion Factors
degree F (°F-32)/1.8 = °C
psi × 6894757 = kPa
Conclusions
In this work a new algorithm for phase envelope generation was suggested. This algorithm does not depend on the derivatives of fugacity and is simpler to program for EOS that has complicated functions of fugacity.
The following additional observations were made for the proposed algorithm:
1. The proposed algorithm works well without any convergence issues.
2. Phase envelopes can be easily generated for any EOS and without the requirement of partial derivatives of fugacity.
3. This algorithm is best applied to EOS whose fugacity functions are complicated and highly non-linear.
4. This algorithm is verified against the commercial software which uses Michelsen’s algorithm.
5. The modification of Newton-Armijo makes the VLE flash algorithm more robust.
References
- Michelsen ML (1980) Calculation of Phase Envelopes and Critical Points for Multicomponent Mixtures. Fluid Phase Equilibria 4: 1-10.
- Muskat M, McDowell JM (1949) An Electrical Computer for Solving Phase Equilibrium Problems. Trans., AIME 186: 291.
- Wilson G (1968) A Modified Redlich-Kwong EOS, application physical data calculation. Paper 15C presented at the annual AICHE National Meeting, Cleveland, Ohio.
- Kress R (1998) Numerical Analysis. Springer-Verlag Inc., New York.
- Soave G (1972) Equilibrium Constants from a Modified Redlich-Kwong Equation of State. ChemEngSci 27: 1197-1203.
- Peng DY, Robinson DB (1976) A New-Constant Equation of State. IndEng Chem Fund 15: 59-64.
Relevant Topics
Recommended Journals
- Oil & Gas Research Journal
- Renewable Energy and Applications Journal
- Oceanography Journal
- Industrial Pollution Control Journal
- Coastal Zone Management Journal
- Climatology & Weather Forecasting Journal
- Geoinformatics & Geostatistics Journal
- Engineering and Technology Journal
- Petroleum & Environmental Biotechnology Journal
- Polymer Sciences Journal
Article Tools
Article Usage
- Total views: 13152
- [From(publication date):
December-2015 - Mar 31, 2025] - Breakdown by view type
- HTML page views : 12038
- PDF downloads : 1114