Research Article Open Access
Modeling Development and Numerical Simulation of Transient Nonlinear Behaviors of Electric sensitive Hydrogel Membrane under an External Electric Field
| Zhen Yuan1,2* and Hua Li3 | ||
| 1Center for Strategic Communication, Arizona State University, POB 871205, Tempe, AZ 85287-1205, USA | ||
| 2Department of Biomedical Engineering, University of Florida, Gainesville, FL 32611, USA | ||
| 3School of Mechanical and Aerospace Engineering, Nanyang Technological University, Singapore | ||
| Corresponding Author : | Zhen Yuan Department of Biomedical Engineering University of Florida Gainesville, FL 32611, USA E-mail: yzhen.star@gmail.com |
|
| Received November 20, 2012; Accepted December 07, 2012; Published December 14, 2012 | ||
| Citation: Yuan Z, Li H (2013) Modeling Development and Numerical Simulation of Transient Nonlinear Behaviors of Electric-sensitive Hydrogel Membrane under an External Electric Field. J Biochips Tiss Chips 3:103. doi:10.4172/2153-0777.1000103 | ||
| Copyright: © 2013 Yuan Z, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. | ||
Related article at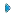 Pubmed Pubmed  Scholar Google Scholar Google |
||
Visit for more related articles at Journal of Bioengineering and Bioelectronics
Abstract
A multi-physics model is developed to predict the transient nonlinear behavior of electric-sensitive hydrogel membrane, based on a multi-phasic mixture theory. In the developed model involving chemo-electro-mechanics, the transient convection-diffusion equations for ionic concentrations incorporate the migration and diffusion terms; the Poisson equation is employed to compute the distribution of electric potential directly, and the transient hydrogel deformation is implemented easily by the continuity and momentum equations. To solve the present mathematical model consisting of transient nonlinear partial differential governing equations, a true meshfree, implicit numerical scheme is conducted for solution of convection-diffusion problem and hydrogel deformation, iteratively. Unlike the mesh-based
methods, the employed meshless Hermite Cloud Method (HCM) uses a fixed reproducing kernel approximation for construction of the interpolation functions, and employs the point collocation technique for discretization of partial differential boundary values and initial value problems. The transient responds of electric-sensitive hydrogels, including the membrane deformation, ionic concentrations and electric potentials, interior and exterior the membranes are numerically simulated, and the parameters having important influence on the transient hydrogel deformation are also investigated.
| Keywords | |
| Hydrogels; Membrane; Multiphasic mixture theory; Mathematical model; Diffusion; Convection; BioMEMS; Meshless method; Biomechanics | |
| Introduction | |
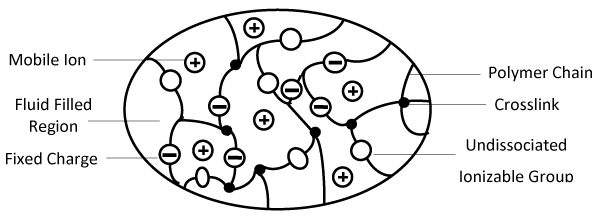
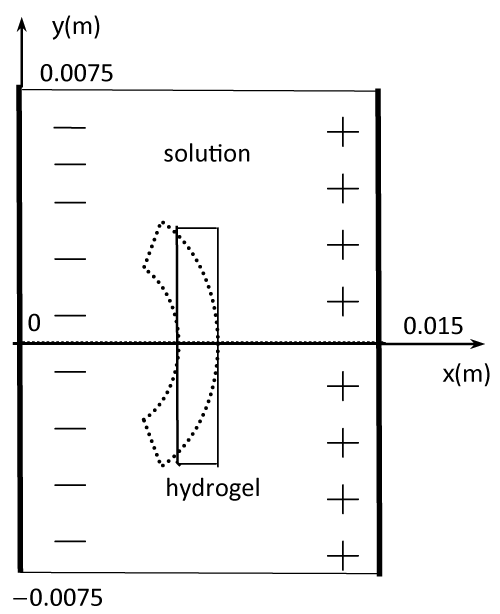
| Over the past decades, the actuators/sensors based on stimuliresponsive polymer hydrogels have attracted much attention for widerange biological applications, such as artificial muscles and Bio-MEMS [1-3]. Their reversible volume changes can be induced by external bio-stimuli including pH, light, temperature and electric field. Usually, hydrogel membranes are composed of the solid, interstitial water and ion phases. If an external electric field is applied, the electric-stimuli responsive hydrogel membranes with fixed-charge groups can bend reversibly, when they are immersed into a bathing-solution (Figures 1 and 2). A number of experimental studies and numerical simulations were performed to investigate the electric-sensitive behaviors of hydrogels which covered the preparation of such materials, studies of deformation mechanism and design of actuators. Tanaka et al. [4] reported a gel collapsed in an acetone/water mixture applied by electric field. Osada et al. [5] reported a polymer gel with electrically driven motility, and Kim et al. [6] studied the electric sensitive behavior of IPN hydrogel. Homma et al. [7,8] and Fei et al. [9] discussed the factors having important effects on the swelling deformation of electricsensitive hydrogels. Sun and Mak [10] studied the mechano-electrochemical behavior of chitosan composite fibers by experiment. Doi et al. [11], Shiga et al. [12] and Shahinpoor [13] investigated the dynamics of ionic polymer gels, subject to an external electric field. Brock et al. [3] studied the dynamic model for electric-sensitive hydrogels, with large-deformation. Nemat-Nasser and Li [14] developed an electromechanical model for ionic polymer metal composite. Accordingly, Neubrand [15] and Grimshaw et al. [16] developed electro-chemical model and electro-mechanical model for ion-exchange membrane and gel, respectively. Recently, Wallmerperger et al. [17] and Zhou et al. [18] made further studies of electric-sensitive hydrogel membranes. However, the multi-physic characteristics of the hydrogels are yet not fully understood, and now under extensive investigations. | |
| The multi-phasic mixture theory was early developed by Lai et al. [19-21] or the swelling and deformation behaviors of articular cartilage. Based on this theory, a new multi-physics model is developed, where the governing equations are composed of the continuity equation, describing the transient deformation of solid phase, the transient convection-diffusion equations computing the diffusive ionic concentrations, the Poisson equation calculating the electric field, and the momentum equation describing the mechanical field. To solve the governing equations with remeshing requirement in hierarchical iteration procedure, a true meshfree, implicit numerical scheme is conducted. The meshless Hermite-Cloud Method (HCM) based on a fixed kernel approximation is used for spatial discretization, in which the interpolation functions are constructed according to a set of points scattered in problem domain. The point collocation technique is employed in the problem domain for discretization of the governing equations, boundary and initial conditions. By the meshless implicit numerical scheme, the transient nonlinear partial differential governing equations are solved to simulate the distributions of diffusive ionic concentrations and electric potentials, interior and exterior the hydrogel membranes, as well as the swelling and bending deformations of the hydrogels. Moreover, several parameter having important influences on the transient hydrogels deformations are also investigated to enhance the understanding of the chemo-electro-mechanical coupled behaviors of the smart hydrogel membranes. | |
| Model Development of Electro-stimulus-sensitive Hydrogel Membrane | |
| Multi-phasic mixture theory | |
| The classical triphasic and multi-phasic mixture models [19-22], developed for simulation of charged hydrated biological soft tissues is extended to study the transient nonlinear behaviors of charged hydrogel membrane. Based on the multi-phasic mixture theory, this investigation conducts a novel mathematical model to investigate the multi-physics behaviors of the porous membrane applied by an external electric field. The main governing equations of the multi-phasic mixture model are given by Lai et al. [19-21] and Hon et al. [22]. | |
| The saturation condition, | |
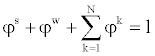 (1) (1) |
|
| The continuity equations | |
 (2) (2) |
|
| The conservation of fixed charge groups attached on the polymer network | |
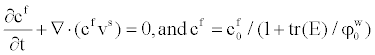 (3) (3) |
|
| The continuity equation of mixture phase by neglecting |
|
| The momentum equations, without the effects of body and the inertial forces | |
| Mixture phase |
|
Water phase 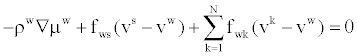 (6) (6) |
|
The kth ion phase 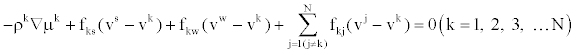 (7) (7) |
|
| The electro-neutrality condition | |
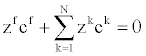 (8) (8) |
|
| The constitutive equations | |
 (10) (10) |
|
| The parameters definitions of the multi-phasic theory are indicated in table 1. | |
| Model development based on modified multi-phasic mixture theory | |
| As described above, the classical triphasic and multi-phasic mixture models are unable to directly calculate the distribution of electrical potentials due to the use of electro-neutrality condition. The migration and diffusion terms aren’t considered in the ionic continuity equations, and the solving domain only covers the hydrogel membranes. To overcome the drawbacks mentioned, a novel mathematical model based on modified multi-phasic mixture theories is developed, and the governing equations are derived as follows. | |
| By summarizing Equations (6) to (7) for all N ionic species, and neglecting |
|
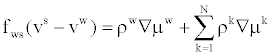 (12) (12) |
|
| Substituting the constitutive equations (10)-(11) into equation (12), and assuming the osmotic coefficients of all ionic species equal to Φ, the equation (12) is rewritten, | |
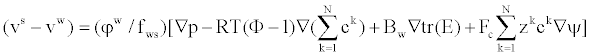 (13) (13) |
|
| It is noted, the continuity equation (4) can be rewritten as | |
| Substituting Equation (13) into Equation (14), the continuity equation of the mixture phase is obtained, | |
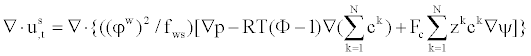 (15) (15) |
|
| Where us is the displacement of the solid phase and Bw is set to zero, since its value is very small [23,24]. | |
| In order to incorporate the effects of migration and diffusion, the Nernet-Planck type of convection-diffusion equations for each diffusive ionic flux, replacing the continuity equation (2) of the ionic phase, is employed, | |
| Moreover, as the velocity of propagation in the electric field is much higher than the one occurring in the convection-diffusion equation, the Poisson equation is given by, | |
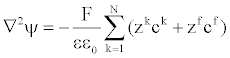 (17) (17) |
|
| where |
|
| And the interfacial conditions at hydrogels-solution interfaces, | |
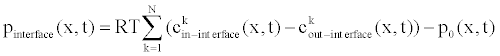 (20) (20) |
|
| where |
|
| A Numerical Scheme for Developed Mathematical Model based on Meshless HCM | |
| Meshless Hermite-Cloud Method (HCM) | |
| In this section, meshless Hermite-Cloud Method (HCM) [23], is introduced for the spatial discretization of the above nonlinear partial differential initial value problems. As an extension of the classical Reproducing Kernel Particle Method (RKPM) [25-27], this meshless approach employs Hermite theorem for the construction of the interpolation functions, and uses the point collocation technique for discretization of Partial Differential equations with Boundary Value (PDBV) problems. | |
| For any unknown real function |
|
 (22) (22) |
|
| Where NT and |
|
| In which |
|
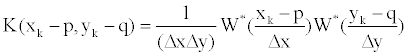 (24) (24) |
|
| And |
|
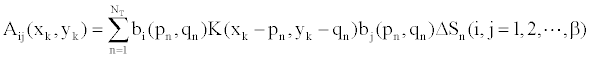 (27) (27) |
|
| In the equation (25), |
|
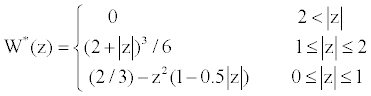 (28) (28) |
|
| Where |
|
| Assuming |
|
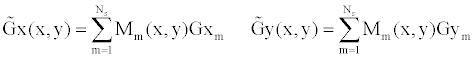 (29) (29) |
|
| It is noted that, compared with the shape functions |
|
| The auxiliary conditions are required for the additional unknown functions |
|
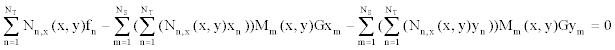 (30) (30) |
|
 (31) (31) |
|
| The meshless method employs the Hermite interpolation theorem to construct the approximate unknown function |
|
| Developed numerical scheme for convection-diffusion problems | |
| An implicit numerical scheme is developed to solve the transient nonlinear convection-diffusion equations (15) and (16), and a Newton iteration process is also implemented for each time step. In consideration of the general case, the convection-diffusion equation is given by | |
| Together with the general boundary and initial conditions | |
| In which k is the diffusion coefficient, v is the convection coefficient,c1, c2 are known constants, and f(x,t) and |
|
| If we define |
|
| Where |
|
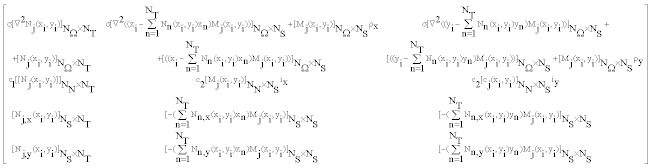 (37) (37) |
|
| Equation (36) can be rewritten, | |
| Where | |
| In which | |
| And | |
| Numerical Validations | |
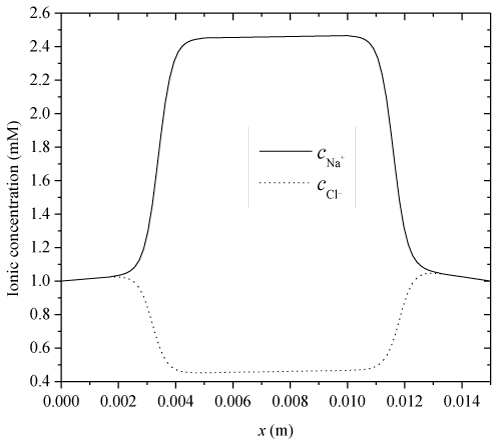
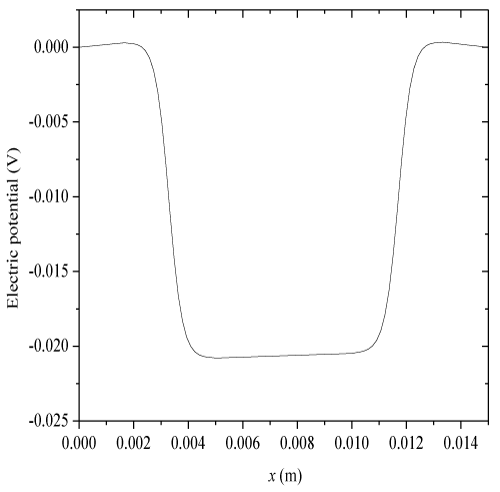
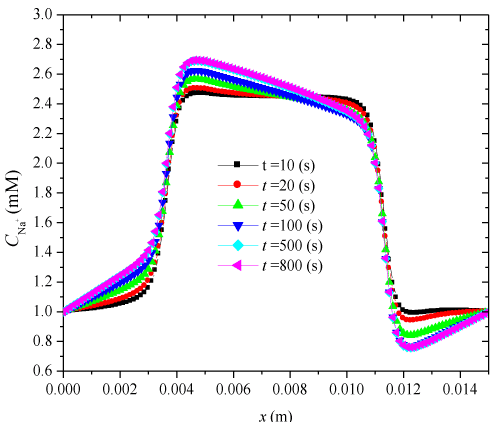
| To validate the presently developed model, several one-dimensional numerical simulations are implemented for the transient membrane deformation in the thickness h direction of strip-like electric-sensitive hydrogels, immersed into bathing solution under an external electric field (Figure 2), where it is assumed that the diffusive coefficients |
|
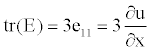 (41) (41) |
|
| Where |
|
| Where e1 and e2 indicate the swelling strains at the two ends of hydrogels thickness. To investigate the transient nonlinear behaviors of electric-stimulus responsive hydrogels, one-dimensional numerical simulations are carried out for a hydrogel strip immersed into NaCl solution applied by an externally applied electric field. In the solution domain x (m) ∈[0, 0.005] ∩ [0.010, 0.015], the Dirichlet boundary conditions for ionic concentrations and electrical potential at anode and cathode are imposed at x=0 and 15×10-3(m), respectively. The specified parameters are |
|
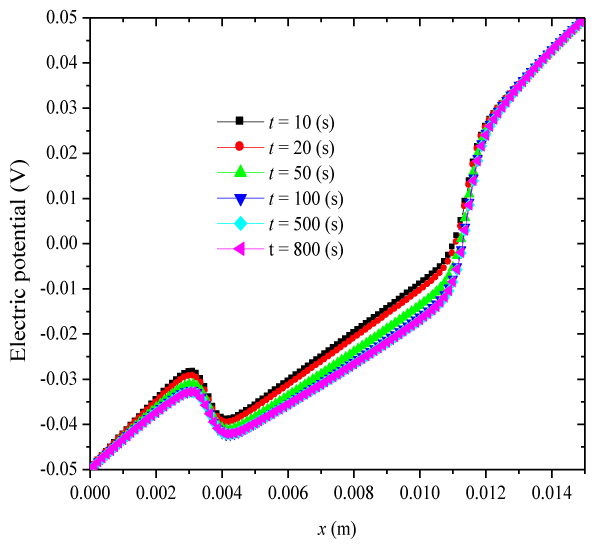
| In this validation, a time-constant external electric voltage Ve=0.1(V) is applied, c0f=2(mM), Zf=−1, h=5×10−3 (m), |
|
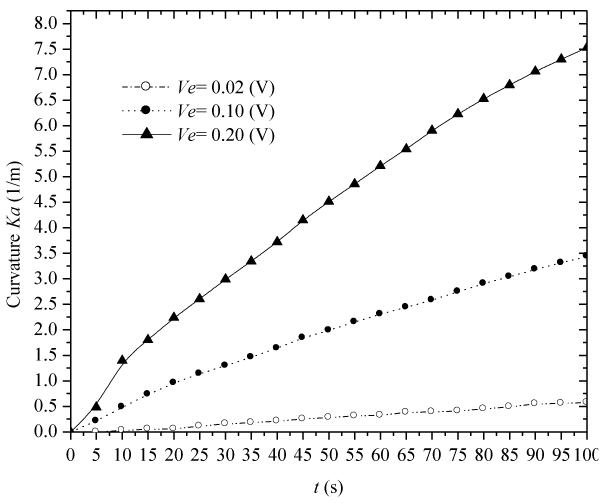
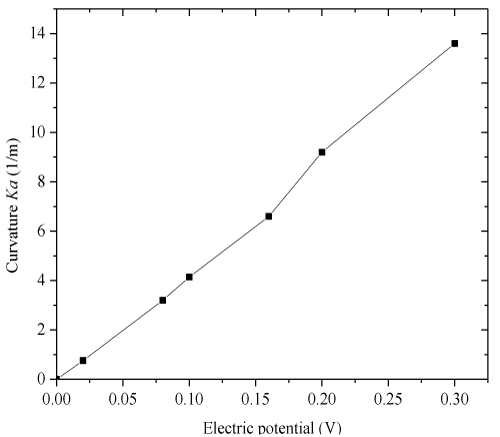
| Figure 9 displays the transient bending deformation of the hydrogel strip subject to different electric voltages, where h=5×10−3(m), |
|
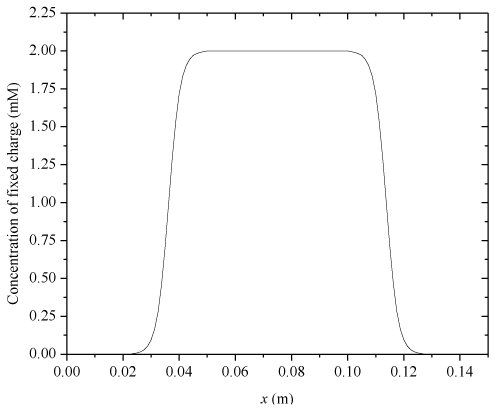
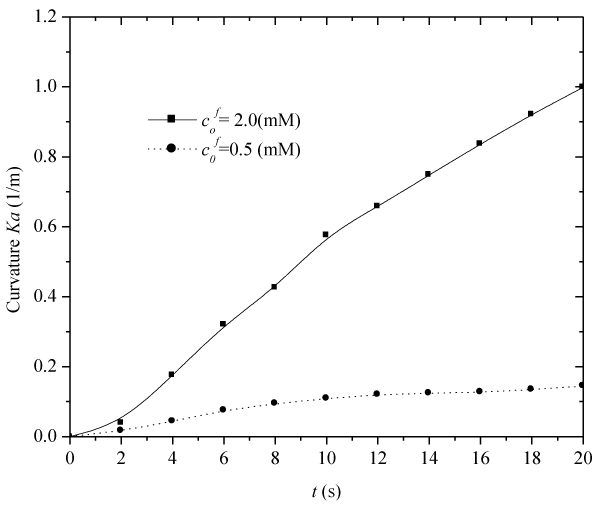
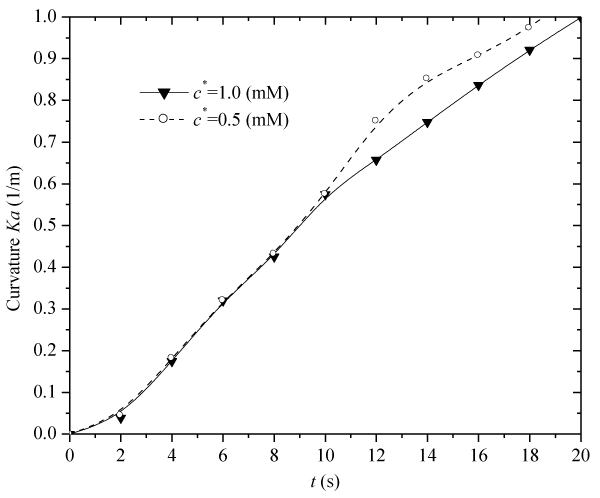
| Figure 11 demonstrates the influence of fixed-charge concentration c0f on the transient average bending curvature Ka, under an externally applied electric field, where Zf=−1, h=5×10−3(m), |
|
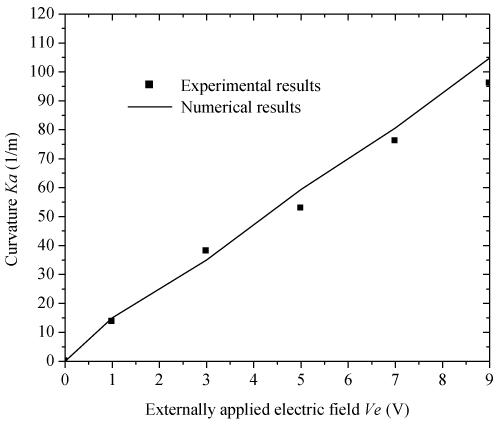
| Numerical simulation for a steady-state case is conducted to investigate the hydrogel membrane deformation and compared with experimental data [18,30]. The parameters used are |
|
| Conclusions | |
| In this study, a multi-physics mathematical model is developed for simulation of the transient nonlinear behaviors of electric-sensitive hydrogel membranes immersed into bathing solution, subject to an externally applied electric field. The formulation is capable to describe the bending deformation of the hydrogel, the distributions of diffusive ionic concentrations, and electric potential in both the interior membrane and exterior solution. One-dimensional numerical simulations are carried out for a hydrogel strip. The numerically simulated results are in good agreements with experimental data and published FEM solutions, which validates the presently developed models. | |
| References | |
|
|
Tables and Figures at a glance
| Table 1 |
Figures at a glance
 |
 |
 |
 |
 |
||||
| Figure 1 | Figure 2 | Figure 3 | Figure 4 | Figure 5 | ||||
 |
 |
 |
 |
 |
||||
| Figure 6 | Figure 7 | Figure 8 | Figure 9 | Figure 10 |
 |
 |
 |
||
| Figure 11 | Figure 12 | Figure 13 |
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 14391
- [From(publication date):
January-2013 - Dec 07, 2025] - Breakdown by view type
- HTML page views : 9714
- PDF downloads : 4677
