Estimating Risk of Mortality from Cardiovascular Diseases using Negative Binomial Regression
Received: 13-Apr-2013 / Accepted Date: 03-Jul-2013 / Published Date: 06-Jul-2013 DOI: 10.4172/2161-1165.1000127
Abstract
Studies have demonstrated that exposure to moderate-to-high levels of ionizing radiations can cause most forms of cancer, leukemia, cardiovascular diseases, stroke, etc., especially at young ages. Hence, study of exposure to radiation has been the subject of intense epidemiological investigation. For experimentation purpose, we have used Hiroshima and Nagasaki atomic bomb survivor data, 1950-2003, Br Med J. 2010, 340:193. We have found this count cohort data to be over dispersed, which has led us to experiment negative binomial regression modelling on it, as it is over-dispersed in itself. We have estimated risk of cardiovascular data w.r.t. dose-category of radiation. As per our model, we have found that doses above 1.25 Gy are associated with an elevated risk of cardiovascular diseases, but the degree of risk at lower doses is unclear.
Keywords: AIC (Akaike Information Criterion); Cohort data; Epidemiology; Over-dispersion; Regression; Relative risk
160254Introduction
Radiation is energy in the form of high speed particles and electromagnetic waves. Everyone is exposed to radiation, in either artificial or natural form [1]. Radiation is classified as ionizing and non-ionizing radiation. Ionizing radiation is radiation with enough energy so that during an interaction with an atom it can remove bound electrons, i.e., it can ionize atoms. e.g. X-Rays and electrons. Nonionizing radiation is radiation without enough energy to remove bound electrons from their orbits around atoms e.g. Microwaves and Visible light. The ionizing radiation interacts with the cells and damages them, resulting in malignant growth in the body, which later, in most of the cases, turns into cancer. Studying impact of radiation on subjects, to check whether it is causing cancer, cardiovascular diseases or stroke to exposed subjects or not, falls under general epidemiological study [2]. Epidemiology is the study of the distribution and determinants of disease prevalence in man. Epidemiologists seek to describe the populations at risk and to discover the causes of diseases. This entails quantification of the risk of disease and its relationship to known or suspected causal factors. In radiation epidemiology, exposure to radiation is the factor of primary interest, and epidemiologists seek to relate risk of disease to different levels and patterns of radiation exposure. Epidemiological studies have been of particular importance in assessing the potential human health risks associated with radiation exposure. If the disease rate is higher among those exposed to radiation, there is a positive association. If the disease rate is higher among the unexposed group, there is a negative (inverse) association between radiation exposure and disease. This is further defined in more precise way by calculating risk of disease w.r.t particular causal factor.
Data Set Used
For experimentation purpose, we have used Hiroshima and Nagasaki atomic bomb survivor data, 1950-2003, Br Med J. 2010, 340:193. The data set is a detailed tabulation of person-years, casecounts, and summary data constructed from data on individual survivors [3]. The cohort for analysis includes 86,661 survivors. Data on individual survivors are stratified by city, sex, age at exposure, attained age, calendar time, and dose. The first six variables, namely, city, sex, agex cat, age cat, ctime and dosecat index the cross-classification used to define the table. The next five variables, i.e. subjects, pyr, agex, age and colon10, include the cell-specific numbers of subjects entering the study, numbers of person-years, and mean values for age at exposure, attained age, and radiation dose (colon). The next eight variables are circulatory disease (cvd), stroke, heartd, othcvd, Circulatory Disease (conCVD), constroke, conheartd and conothcvd, and gives disease death counts. Among these different independent causal factors, we are defining risk of cardiovascular disease, stroke and heart diseases mainly w.r.t. Dosecat (DS02 weighted colon dose categories (i.e. gamma+10*neutron).
Risk Estimation Models
Statistical procedures aim at the following:
i. To estimate the effects of risk factor(s) on rates by condensing the information present in the large set of incidence or mortality rates into a few summary measures.
ii. Evaluating the statistical significance of the effect estimates at different levels of exposure so as to rule out the possibility that the observed differences in rates were due to play of chance.
iii. Estimation of risk factor effects.
iv. Test of Hypotheses. To estimate risk we have used multiplicative model of risk estimation.
Multiplicative risk model
The basic data consists of the counts of deaths djk and the personyears denominators njk in each cell, together with p-dimensional row vectors xjk = (x1jk,.......,xpjk) of regression variables [4].
A general form of the multiplicative model is
log λjk=αj+xjkβ (1)
where the λjk are unknown true disease rates, the αj are nuisance parameters specifying the effects of age and other stratification variables, and β = (β1, …, βk)T is a p-dimensional column vector of regression coefficients that describe the effects of primary interest. An important feature of this model is that disease rates depend on the exposures only through the quantity αj+xjkβ, which is known as the linear predictor. If the regression variables xjk depend only on the exposure category k and not on j, then the above equation specifies a purely multiplicative relationship such that the ratio of disease rates λjk/λjk’, for two exposure levels k and k’, namely exp(xk-xk’) β, is a constant over the strata. A total of K-1 such indicator variables are needed to express the relative risks associated with the different exposure categories, the first level (k = 1) typically being used as a reference or baseline category.
Regression
To quantify significant causal factors and their effect on dependent variable, we have studied different curve fitting models and we have chosen regression models as part of our study because of the following reasons:
1. In statistics, Regression analysis is a statistical tool for the investigation of relationships between variables [5].
2. Regression models are used to predict one variable from one or more other variables. Regression models provide a powerful tool, allowing predictions about past, present, or future events to be made with information about past or present events [6].
3. Regression models are statistical models which describe the variation in one (or more) variable(s) when one or more other variable(s) vary. Inference based on such models is known as regression analysis [7]. A general regression model consists of a function describing how one variable (the response variable) is related to one or more other variables (explanatory variables), and a term which models the random variation in the response variable [8].
Types of Regression Analyses are:
1. Simple Linear Regression
2. Multiple Regression
3. General Linear Models
For Count Data we use
1. Poisson Regression
2. Negative Binomial Regression
Poisson and negative binomial regression
The Poisson (log-linear) regression model is the most basic model that explicitly takes into account the nonnegative integer-valued aspect of the dependent count variable [9]. In this model, the probability of an event count yi, given the vector of covariates xi, is given by the Poisson distribution:
P(Yi = yi|Xi) =e-μi μi yi/yi ! Yi=0,1,2,.......
The mean parameter μi (the conditional mean number of events in period i) is a function of the vector of covariates in period i:
E(yi|Xi) = μi = exp(xi’β)
where β is a (k+1) x1 parameter vector.
(The intercept is β0, and the coefficients for the k covariates are β1… βk)
Taking the exponential of xi’β ensures that the mean parameter μi is nonnegative. The name log-linear model is also used for the Poisson regression model because the logarithm of the conditional mean is linear in the parameters
ln[E(yi|Xi)] = ln(μi) = xi’β
The Poisson regression model assumes that the data are equally dispersed, that is, the conditional variance equals the conditional mean. Real-life data are often characterized by over-dispersion, that is, the variance exceeds the mean. The negative binomial regression model is a generalization of the Poisson regression model that allows for over-dispersion by introducing an unobserved heterogeneity term for observation i. Observations are assumed to differ randomly in a manner that is not fully accounted for by the observed covariates.
In the negative binomial model,
E(yi|Xiτi) = μiτi = exi’βτi
where τi follows a gamma(O, O) distribution with E(τi) = 1 and V(τi) = 1/O
Existing Model
Radiation effects Research Foundation has done very important work in the context of radiation exposure and circulatory disease and has published in 2010 [10]. The main outcome of the disease has been attributed to higher levels of radiation exposure. According to [10], for stroke the estimated excess relative risk per gray was 9% (95% confidence interval 1% to 17%, p=0.02). Similarly for heart diseases, the estimated relative risk was 14% (6% to 23%, p<0.001) [10]. The results of the work indicated that linear dose-response model provided the best fit over dose values of 0.5 Gy. Moreover prospective data on smoking, alcohol intake, education, occupation, obesity and diabetes had almost no impact on the radiation risk estimates for either stroke or heart disease and misdiagnosis of cancers as circulatory diseases could not account for the associations seen. In [10], the analysis was done using Poisson Regression methods for grouped survival data to describe the dependence of risk on radiation dose and to evaluate the variation of the dose-response effects with respect to city, sex, age at exposure, time since exposure, attained age, which is essentially identical to the methods used to examine mortality from cancer in this cohort. The modelling was done using EPICURE software which was developed, that allows for modelling of both relative and absolute risks, including fitting the linear RR models. The primary models used here are the Excess Relative Risk (ERR) models of the form
λ0(c,s,a, b)[1 + ERR(d, e, s, a)]
where λ0() is the baseline, or background death rate(that is the death rate for people with zero dose), which depended on the city(c), sex(s), attained age(a) and birth year (b). The function ERR(d,e,s,a) describes the relative changes in rates associated with dose(d), allowing for effects of sex, age at exposure (e), and attained age (a).The effect modifiers were examined too in [10]. The dose and dose squared terms were examined to evaluate the degree of linearity or curvature in the dose-response forms. In addition to these models, linear threshold model was evaluated for a wide range of possible values of threshold dose (d0), modeling the risk function ERR on doses d as β(d - d0) for d > d0 or d = 0 for d < d0. In radiation epidemiology [11,12], Linear Relative Risk Model plays a prominent part, in which the RR is a linear function of dose. In its simplest form
RR(D) = 1 + β(D)
where D is the dose, RR(D) is the relative risk at dose D, and β is the ERR per unit of dose, which is usually expressed in grays or sieverts. The linear model has been used extensively in A-bomb studies, person exposed for medical reasons, and nuclear workers. The model has served as the basis of cancer risk estimation by three BEIR committees and by the National Institute of Health (NIH 2003). The linear model has been chosen because it fits the data from most studies (although in many studies, statistical power is inadequate to distinguish among different dose-response functions).
Negative Binomial Regression Over Poisson Regression
It is often observed that count data is over-dispersed. The data is said to be over-dispersed when the variance of the data is greater than its mean [13]. So, in our case, we have checked for the over-dispersion of count data, i.e. for cvd, stroke and heartd. In case of cvd, variance is about ten times greater than the mean. For stroke and heartd, variance is about five times greater than its mean. This implies that the provided count data is over-dispersed.
Assumptions in Poisson regression model - In our case, we can assume that we can specify variance as follows [11]
Var (Y) = ɸ E(Y) = ɸμ
In case of Poisson it is assumed that ɸ=1. Hence, even if we have situation where ɸ >1, Poisson’s estimations will be consistent. Thus, Poisson standard errors tend to be conservative in the presence of overdispersion.
The negative binomial distribution is best known as the distribution of the number of failures before k successes in a series of Bernoulli trials, with common probability of success π. The resulting density can be obtained from the expression above setting α= k and π = β/ (μ + β).
The negative binomial distribution with α = β = 1/σ2 has mean
E(Y) = μ
And variance
Var (Y) = μ/ (1 + σ2μ)
If σ2 is zero we obtain the Poisson variance.
If σ2> 0, then the variance is larger than the mean. Thus, the negative binomial distribution is over-dispersed relative to the Poisson.
Thus we have chosen negative binomial regression with multiplicative model for estimating risk.
Experimental Results
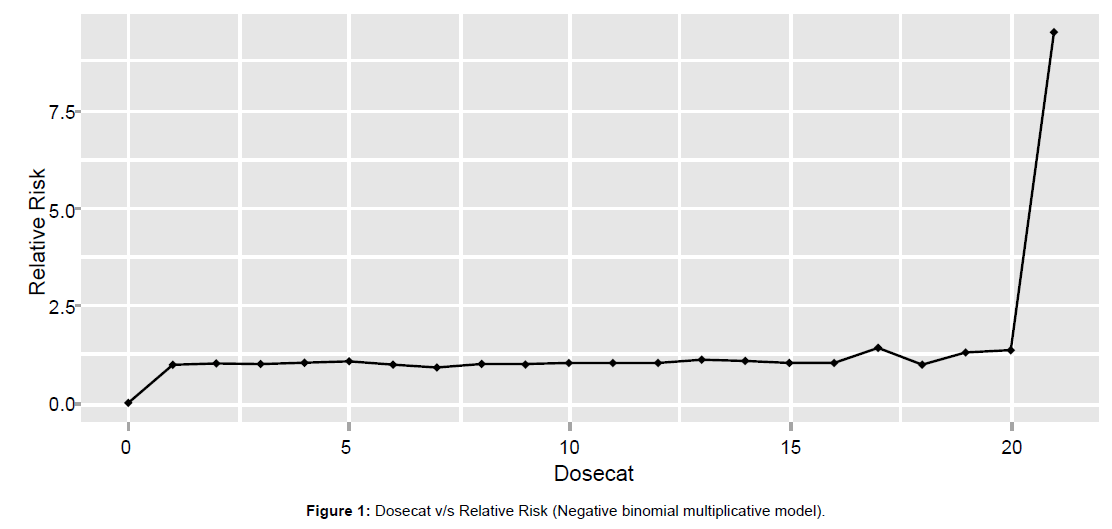
Using regression subset methods, we have found that age at exposure category, age, city, sex, dose category are the most significant causal factor, which elevates the risk of all the cardiovascular diseases together. Figure 1 shows graph of Relative Risk w.r.t. dose category. Graph shows that after dose category 17, there is rise in risk of cardiovascular disease.
Conclusion
We have built a model using negative binomial regression whose results are then compared with results of existing Poisson model using certain parameters. Summary of comparison is tabulated in Table 1. From the above Table, we can say that negative binomial regression fits the given data of atomic bomb blast survivor of Japan better than Poisson regression model.
| Parameters | Poisson Regression Model | Negative Binomial Regression Model |
|---|---|---|
| AIC | 29993.77 | 29219.63 |
| R2 Value | 0.8831995 | 0.8927297 |
Table 1: Comparison of models.
Future Work
We are seeking some other regression techniques to fit given data. Negative binomial regression model (additive), Zero inflated negative binomial regression model seems to be one possible way. Our count data has over-dispersion and excess zeros [14]. Zero inflated count models provide a parsimonious yet powerful way to model this type of situation. Such models assume that the data are a mixture of two separate data generation processes: one generates only zeros, and the other is either a Poisson or a negative binomialdata-generating process. The result of a Bernoulli trial can be used to determine which of the two processes generates an observation.
Acknowledgements
We would like to express our sincere gratitude to our project guide Dr. Vahida Attar (Assistant Professor), Dr Dutta (BRNS), Mrs. A.B. Patil (Assistant Professor) and Ms. Gauri Dani for giving us the opportunity to work on this topic and for providing their timely guidance and help. It would have never been possible for us to take this project to this level without your innovative ideas and your relentless support and encouragement.
References
- Steven L Simon (2011) Radiation Epidemiology Branch, Division of Cancer Epidemiology and Genetics, National Cancer Institute, Introduction to Radiation Physics and Dosimetry.
- Health Risks from Exposure to Low Levels of Ionizing Radiation: Background for Epidemiological Methods, BEIR VII Phase2, Board on Radiation Effects Research (BRER) (2006) NATIONAL RESEARCH COUNCIL of the NATIONAL Academies, THE NATIONAL ACADEMIC PRESS Washington, D.C.
- lsscvd10.dat (2010) Life Span Study Circulatory Disease Mortality Data, 1950-2003.
- NE Breslow, NE Day Methods in Cancer Research Volume II - The Analysis of Cohort Studies.
- Alan O Sykes (1992) The Inaugural Coase Lecture: An Introduction to Regression Analysis.
- David W Stockburger (1996) Introductory Statistics: Concepts, Models, and Applications.
- Erdman D, Jackson L, Sinko A, SAS Institute Inc. (2008) Zero-Inflated Poisson and Zero-Inflated Negative Binomial Models Using the COUNTREG Procedure. SAS Global Forum 2008.
- Shimizu Y, Kodama K, Nishi N, Kasagi F, Suyama A, et al. (2010) Radiation exposure and circulatory disease risk: Hiroshima and Nagasaki atomic bomb survivor data, 1950-2003. BMJ 340: b5349.
- Piza EL (2012) Using Poisson and Negative Binomial Regression Models to Measure the Influence of Risk on Crime Incident Counts. Rutgers Center on Public Security.
Citation: Charkha N, Ghatge A, Sharma P, Attar VZ, Patil AB (2013) Estimating Risk of Mortality from Cardiovascular Diseases using Negative Binomial Regression. Epidemiol 3:127. DOI: 10.4172/2161-1165.1000127
Copyright: © 2013 Charkha N, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided theoriginal author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 16839
- [From(publication date): 6-2013 - Nov 29, 2025]
- Breakdown by view type
- HTML page views: 11862
- PDF downloads: 4977