Research Article Open Access
GC/MS Determination of N-butyl-N-(3-carboxypropyl) Nitrosamine (BCPN) in Bladder Cancers - The Skewed Molecular Interaction CausedRetention Time Shift
Chiu-Lani Hsieh1, Huir-Er Wang2, Yaw-Bee Ker2, Chiung-Chi Peng3,4,5, Kuan-Chou Chen6,7* and Robert Y. Peng8,9*
1Graduate Institute of Biotechnology, Changhua University of Education, Jin-De Campus, 1 Jin-De Rd., Changhua 50007, Taiwan
2Institute of Food Science and Technology, Hungkuang University, 34 Chung-Chie Rd., Shalu County, Taichung Hsien, 43302 Taiwan
3Department of Physical Therapy, Hungkuang University, 34 Chung-Chie Rd., Shalu County, Taichung Hsien, 43302 Taiwan
4Graduate Institute of Rehabilitation Science, Hungkuang University, 34 Chung-Chie Rd., Shalu County, Taichung Hsien, 43302 Taiwan
5Department of Nutrition, College of Health Care, China Medical University and Hospital, 91 Hsueh-Shih Rd., Taichung, Taiwan 40202
6Department of Urology, Taipei Medical University-Shuang Ho Hospital, Taiwan
7Taipei Medical University, 250, Wu-Xin St., Xin-Yi District, Taipei, Taiwan
8Research Institute of Biotechnology, Hungkuang University, 34 Chung-Chie Rd., Shalu County, Taichung Hsien, Taiwan 43302
9Research Institute of Medical Sciences, Taipei Medical University, 250 Wu-Xin St., Xin-Yi District, Taipei 110
- *Corresponding Author:
- Dr. Kuan Chou Chen
Department of Urology,Taipei Medical University-Shuang Ho Hospital
Tel: +886-2-27299723
E-mail: kc.chen416@msa.hinet.net
Dr. Robert Y. Peng
Research Institute of Biotechnology, Hungkuang University
34 Chung-Chie Rd., Shalu County
Taichung Hsien Taiwan 43302
Tel: +886-2-27585767, +886-952-002-092
E-mail: ypeng@seed.net.tw
Received date: December 26, 2010; Accepted date: February 11, 2011; Published date: February 16, 2011
Citation: Hsieh CL, Wang HE, Ker YB, Peng CC, Chen KC, et al.(2011) GC/ MS Determination of N-butyl-N-(3-carboxypropyl) Nitrosamine (BCPN) in Bladder Cancers - The Skewed Molecular Interaction Caused Retention Time Shift. J Anal Bioanal Tech 1:115. doi: 10.4172/2155-9872.1000115
Copyright: © 2011 Hsieh CL, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Analytical & Bioanalytical Techniques
Abstract
N-butyl-N-(4-hydroxybutyl) nitrosamine (BBN) has been widely used in rodents as an invaluable experimental tool for investigation of bladder cancer (BCA). The urinary level of its metabolite, N-butyl-N-(3-carboxypropyl) nitrosamine (BCPN) was reported to be a very reliable predicative parameter of BCA. However, in determination of the urinary BCPN we found the retention time (tR) of BCPN was randomly damping. The tR values of the authentic BCPN at 5, 10, 20, 50, and 100 ppm were 28.48, 27.59, 27.43, 28.00, and 28.32 min comparing with 28.23 min of the urinary BCPN in HPLC analysis, similarly, 17.30 min for the urinary and the 18.00 min for the authentic BCPN in GC/MS analysis. To interpret such a damping, we theoretically proposed that a certain transient skewed molecular interaction could occur during the chromatographic separation, which would cause a certain degree of fluctuation on the tR of target molecules. Conclusively, the retention time of a chemical is not a definite value as often considered in HPLC and GC/MS analyses. In reality it fluctuates depending mainly upon the interaction among a cluster of coexisting molecules, in particular, when operated at higher concentrations.
Keywords
N-butyl-N-(4-hydroxybutyl) nitrosamine; N-butyl-N- (3-carboxypropyl) nitrosamine; bladder cancer; HPLC; GC/MS
Introduction
As N-butyl-N-(4-hydroxybutyl) nitrosamine (BBN) can induce bladder cancer very similar to transitional cell carcinoma in patients in both kinetics and histologic features, hence has been widely used in animal modeling [1–3].
Currently, cigarette smoking has been considered to be an epidemiological major risk factor of developing bladder cancer in industrialized countries. While N-nitroso compounds (NOCs) have been proposed as etiologic agents of bladder cancer associated with Schistosomiasis [1-3], N-nitrosodibutylamine (NDBA) is the first chemical identified as a rat bladder carcinogen that has been detected in tobacco smoke. Although at low concentrations, it is considered practically carcinogenic to humans [4]. NDBA is metabolized mainly in liver. Its tumor inducing capability in rat bladders seems to depend on the formation of two ω-oxidized metabolites, N-nitrosobutyl (4-hydroxybutyl) amine (BBN) and its proximate carcinogen N-nitrosobutyl (3-carboxypropyl) amine (BCPN) [5]. Physiopathologically, BBN-induced urinary bladder carcinogenesis in rodents is an excellent model system to understand the carcinogenic mechanisms by NOCs [6].
Several lines of epidemiologic and experimental evidence suggest that a decreased expression in carcinogen-detoxifying enzymes, such as N-acetyl transferase 2 [7,8], glutathione S-transferase (GST) M1 [7,9], NAD (P) H quinone oxidoreductase [10], and UDPglucuronosyltransferase (UGT) 1A [11], is associated with urinary bladder cancer. BCPN, the major urinary metabolite of BBN, has been shown to have carcinogenic effects on urothelial cells [12,13]. Following α-hydroxylation, BCPN and BBN are chemically cleaved to their corresponding alkylcarbonium ion that binds covalently to DNA and enhances carcinogenesis [14] (see Appendix Figure A1 [15]).
Theoreticals
To discuss the molecular interaction in a binary component system, we have first to introduce the solubility parameter, δ which is defined as
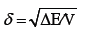 (1)
(1)
where ΔE is the energy of vaporization to gas at zero pressure (i.e. infinite separation of the molecules); V is the molar volume; while the ratio ΔE/V is always defined as the cohesive energy density (CED).
Alternatively, the Flory-Huggins equation (Eq. 2) [16] is the very popularly cited equation to discus the interaction between (or among) the molecules by considering the difference of solubility parameters.
X1,2=([ΔHm/kTN1v2]= β12 + (v1/RT) (δ1-δ2)2 (2)
Here the symbol X 1,2 on the left hand side denotes the Flory- Huggins molecular interaction parameter of a solvent with the polymer; ΔHm means the enthalpy change of mixing; k is the Boltzmann constant; T is the absolute temperature in Kelvin scale at which the experimental data are developed; N1 is the number of molecules of species 1; v2 is the molar volume of molecular species 2; v1 is the molar volume of molecular species 1; R is the gas constant; δ1 and δ2 denote the solubility parameters of molecular species 1 and 2, respectively. And the parameter β12 is the interaction parameter under conditions completely soluble or miscible, i.e. under condition δ1= δ2 (Eq. 2). The best condition for solute-polymer interacting pair is β12=0.35 [16]. Thus the smaller the difference between the solubility parameters, the more likely one chemical could be dissolved in or miscible with the counterpart solute.
Assuming the Eq. 2 is applicable to all situations dealing with the molecular interaction, we have for a cluster of molecular event the relationship
ΣXi,j=Σ([ΔHm/kTNivj] = Σ[βI,j + (vi/RT) (δi-δj)2] (3)
Which denotes that the centered target molecule i act with its j surrounding molecules (j = 1, 2, 3,…..j). Obviously, here the vector effect has been omitted for simplification. Consequently, by considering the vector factor, the overall interaction parameter is arbitrarily modified as Σxi,j´ that actually has involved the concept of vector sum.
ΣXi,j´=Σ([ΔHm/kTNivj] = Σ[βi + (vi/RT) (δi-δj)2] (4)
However, in chromatographic analysis, the true situation is more complicate. Using the inverse gas chromatography (IGC) measurement, King obtained the solubility parameter of the solutes [17]. Such a deduction requires the computation of intermediate parameters, namely the solute-solvent interaction parameter, X i,j, which is directly derivable from the specific retention volumes measured in the IGC experiment [17]. Specific retention volumes, VR, for the chosen solutes in the stationary phase can be calculated from the retention time data as previously described by King et al. [18]. These retention volumes are then utilized to compute the interaction parameter, X i,j, between the solute i and solute j according to Eq. 5 [19]. Details of the computation of the specific retention volumes are given in standard texts [20] and will not be repeated here.
Xi,j =[ln273.16 R/VR MiP - Poi (Bii – Vi)/RT]- [ln υi/ υ2] –[1+ Vi/Mjυj] (5)
where R =6.236 × l04 mL-mm Hg/mole-“K
VR = specific retention volumes
Mi =molecular weight of the solute i
Po i =vapor pressure of solute i at column temperature, T
Bii =second pure virial coefficient of the solute i at T
Vi =molar volume of the solute i at T
T = column temperature
υi =specific volume of the solute i at T
υj =specific volume of the solvent j at T
Mj =molecular weight of the solute j
It should be noted when IGC is used to determine X parameters for polymer(i)/solute(j) interaction, that the last two terms in Equation 5 are often omitted, since they contribute negligibly to X for the case of an infinitely high molecular weight polymer [17]. This is not the case, however, for a solute having a low molecular weight such as BBN and BCPN, these terms should be computed and used in the calculation of X. To compute the second virial coefficient of the solute, the wellknown relationship developed by McGlashan and Potter [21] as given in Eq. 6 can be applied.
BiiVc= = 0.430 - 0.866(Tc/T) - 0.694(Tc/T)2 - 0.0375 (n -1) (Tc/T)4.5 (6)
where Tc =critical temperature of the solute
Vc =critical volume of the solute
n = hypothetical number of carbon atoms for a given solute that yields a Po 1 equivalent to that of a corresponding n-alkane solute.
The parameter n can be calculated according to the procedure of Guggenheim and wormald [22] and King et al. [18].
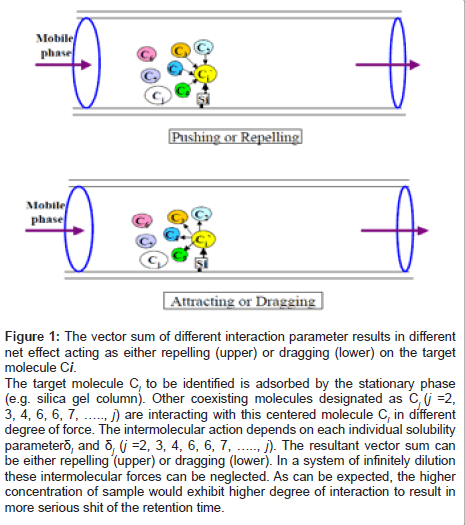
Substitution of the values of Bii obtained from Eq. 6 into Eq. 5 yields e the interaction parameters X i,j for each pair of solutes (Eq. 6). Substitution of the value of X i,j into Eq. 3 in turn leads to the solubility parameter by comparing with the solubility of a reference compound. Obviously, when operated at very low concentration, each molecule would acts freely without any interacting interference from the surrounding molecules. However, as the HPLC or GC operation concentration is increased, the interaction of the surrounding molecules would be also steadily increased. Thus the resultant molecular interaction parameters ΣXi,j could appear as either repelling or dragging (Figure 1), where Ci is the centered target molecule, Cj (j =2, 3,…., j) are the surrounding molecules.
Figure 1: The vector sum of different interaction parameter results in different net effect acting as either repelling (upper) or dragging (lower) on the target molecule Ci.
The target molecule Ci to be identified is adsorbed by the stationary phase (e.g. silica gel column). Other coexisting molecules designated as Cj (j =2, 3, 4, 6, 6, 7, ….., j) are interacting with this centered molecule Ci in different degree of force. The intermolecular action depends on each individual solubility parameter δi and δj (j =2, 3, 4, 6, 6, 7, ….., j). The resultant vector sum can be either repelling (upper) or dragging (lower). In a system of infinitely dilution these intermolecular forces can be neglected. As can be expected, the higher concentration of sample would exhibit higher degree of interaction to result in more serious shit of the retention time.
As similarly treated in Eq. 4, on consideration of the vector factor we have from Eq. 5 the overall effective interaction parameter, Σ?i,j´, along the separation column resulting from a cluster of molecular interactions.
ΣXi,j´ = ΣXi,j cosθij= cosθij {Σ[ln273.16 R/Vg MiP - Po i (Bii – Vi)/RT]- [ln υi/ υ2] –[1 + Vi/Mjυj]} (7)
where θij is the angle of the vector interaction parameter intersecting with the direction of longitudinal axis.
Thus, we predict that the transient molecular cluster surrounding the centered target molecule could induce skewed molecular interactions leading to transient fluctuations on the retention time in an HPLC or GC/MS analysis.
Experimental
Chemicals and materials
Ethyl acetate was manufactured by E. Merck Co. (Germany). N-butyl-N-(4-hydroxybutyl) nitrosamine (BBN) and N-butyl-N-(3- carboxypropyl) nitrosamine (BCPN, 96% in purity) were provided by Kasei Industrial Co. (Tokyo, Japan). Methanol was purchased from Sigma (Mo., USA). Hydrochloric acid was product of Wako Pure Chemicals Inc. (Tokyo, Japan). Micropore (0.2 µm) was a product of Pall Co. (USA).
HPLC analysis of N-butyl-N-(3-carboxypropyl) nitrosamine (BCPN)
The HPLC analysis of BCPN was carried out according to Wada et al. [24]. The HPLC used was the Hitachi HPLC (installed with an L-2130 pump and an L-2480 FL Detector (Hitachi HiTech, Tokyo, Japan). The high speed centrifuge, Mode-3740, was provided by Kubota Co. (Japan). The analytical column used was RP18, Supelco (USA). The ultrasonicator DC200H was purchased from Delta Chemical Sejahtea (Jakata-Indonesia).
Preparation of BCPN standard solution
0.01g of authentic N-butyl-N-(3-carboxypropyl) nitrosamine (BCPN) was accurately measured and dissolved in ddw to make a total volume of 10 mL. This standard solution containing 1000 ppm of BCPN was used as the stock solution of BCPN and kept at 4°C in the dark for further use. The stock solution was successively diluted with ddw to concentrations of 10, 20, 30, 50, and 100 ppm, respectively.
Preparation of fluorescence derivative of BCPN with anthryl diazomethane (ADAM)
Standard solution of BCPN (0.5 mL) was accurately measured and transferred into a 5 mL tube. To which 100 µL of HCl (2 N) and 0.5 mL of ethyl acetate were added and agitated vigorously for 1 min. The solution was centrifuged at 3000xg for 15 min. The upper supernatant layer was separated. The supernatant (0.5 mL) was measured and dried under nitrogen blow. To the residue 0.5 mL of ADAM solution (800 µg/mL in ethyl acetate) was added. The mixture was left for 1 h to facilitate the reaction. HPLC analysis was carried out. The amount of sample injected was 0.3 µL each time. The column type was Hitachi RPC18 (l=150 mm, id=2.0 mm). The mobile phase was a mixture of methanol: water (80:20 v/v/) operated at a flow rate of 0.6 mL/min. The fluorescence was monitored with a fluorescence detector (FL type L-2480) at λEc = 365 nm; and λEm=430 nm.
Determination of urinary BCPN
The urinary level of BCPN was determined according to Ozaki et al. [23] with slight modification. For mass treatment, a precolumn was suggested to be used for purification. Briefly, the separation was performed with a mobile phase consisting of a mixture of acetonitrile and sodium acetate buffer (20 mmol/L, pH 4.5) (3:7 v/v). The flow rate was set at 1 mL/min. The fraction that appeared with a retention time of 7.8 min (BCPN) was collected. The recovery yield of BCPN from the urine was about 60% under our assay conditions. The product BCPN obtained was assayed similarly as mentioned in the above. Alternatively, for simplicity 0.1 mL of urine sample was diluted to 0.5 mL with distilled water. A 3.3-µL aliquot of 12 mol/L HCl was added. The sample was repeatedly extracted with 0.5 mL of ethyl acetate for three times. The organic layers were collected after centrifugation for 5 minutes at 10,000xg and dried in a high speed vacuum concentrator with a cooling trap maintained at 30°C. The residue was dissolved in ethyl acetate and spotted onto a silica gel 70 F254 precoated plate (Wako Pure Chemical Co., Osaka, Japan). The plates were developed with chloroform/methanol/acetic acid (18:1:1, v/v) in the dark. The bands corresponding to BBN or BCPN (The Rf values reported to be 0.68 to 0.72) were scraped off and extracted out off the silica gel with 4 mL of acetone. The extract was concentrated in a high speed vacuum concentrator. The residual viscous portion was redissolved in acetonitrile to a final volume of 0.2 mL and filtered through a MiniSart RC4 filter (0.2-µm pore size; Sartorius, Göttingen, Germany). The filtrate was subjected to HPLC analysis at 239 nm for determination of the urinary BCPN level using Shimazu LC9A HPLC (Shimazu, Kyoto, Japan) installed with a Finepak SIL C18 column (Jasco, Tokyo, Japan; l=250 mm, id = 4.6 mm).
Gas Chromatographic analysis of N-butyl-N-(3-carboxypropyl) nitrosamine (BCPN)
The determination of BCPN with gas chromatography was conducted according to Ozaki et al. [23] and Wada et al. [24] with a slight modification. Briefly, the urine sample was treated with a primary separation column to exclude all possible contaminants. The purified product was dried under a nitrogen flow. 10 mg of the residue was methylated with a mixture of 10% of sulfuric acid and 6 mL of methanol. The reaction mixture was frequently agitated at ambient temperature for 5-6 h to facilitate the reaction. 5 mL of water was added to terminate the reaction. To the mixture 6 mL of chloroform and anhydrous sodium sulfate was added. After agitated vigorously for 2 min, the mixture was left to stand to facilitate the separation. The supernatant was measured and subjected to GC.MS analysis.
Condition of GC/MS operation
The GC/MS GC HP 6890 attached with HP5973MSD detector and a capillary column DB-5 (l= 60 cm, i.d= 0.25 mm, membrane thickness, 0.25 µm) was used. The injection port and the detector were maintained at 270 and 280°C, respectively. The volume of supernatant applied was 1 µL. The ionization potential used was 70 eV where the temperature of ion source was held at 230°C. The temperature of column was programmed as: initially at 40°C for 10 min, then programmed at an elevation rate of 2°C/min until up to 280°C and maintained at which for 30 min. The mobile phase was his gas operated at a flow rate of 1 mL/min.
Results and Discussion
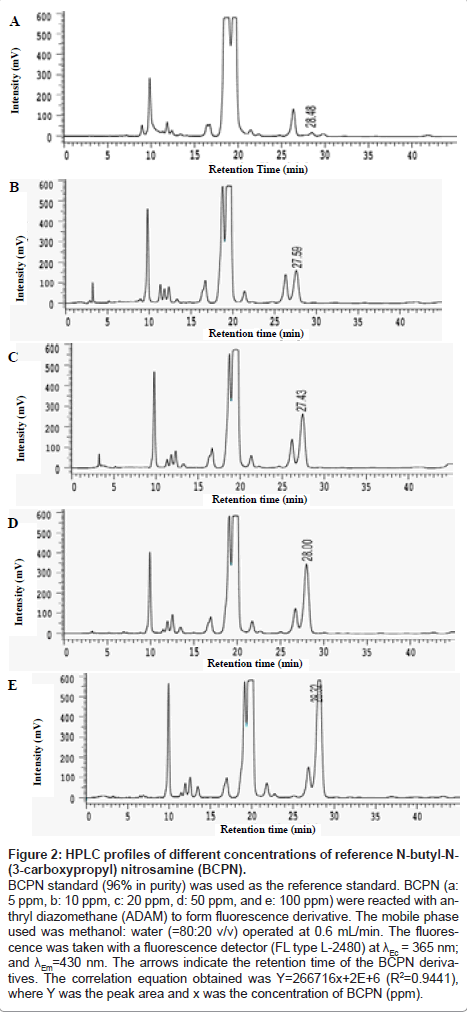
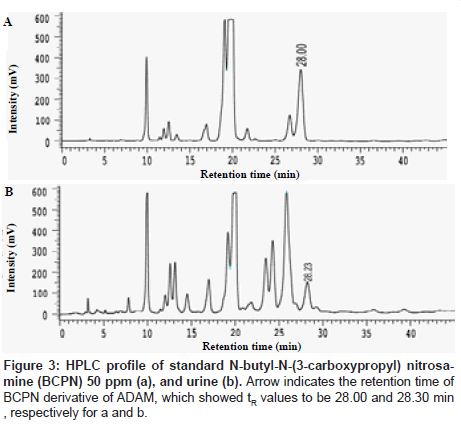
Figure 2 indicate the retention time (tR) of reference BCPN at different concentration. As seen, the tR values of reference BCPN fluctuated randomly at 28.48, 27.59, 27.43, 28.00, 28.33 min, respectively, for 5, 10, 20, 50 and 100 ppm of BCPN. From which a correlation was achieved as Y= 266716 X+2.0×106 (R2=0.9441), where Y is the peak area and X is the concentration of BCPN (ppm) (not shown), whence the content of BCPN in urine specimen having a tR = 28.23 min was calculated to be 12.8 ppm. Moreover, taking the median concentration 50 ppm as a reference point, the tR was also found to have shifted from 28.00 min for reference BCPN (50 ppm) (Figure 3a) to 28.23 min of urinary BCPN (Figure 3b).
Figure 2: HPLC profiles of different concentrations of reference N-butyl-N- (3-carboxypropyl) nitrosamine (BCPN).
BCPN standard (96% in purity) was used as the reference standard. BCPN (a: 5 ppm, b: 10 ppm, c: 20 ppm, d: 50 ppm, and e: 100 ppm) were reacted with anthryl diazomethane (ADAM) to form fluorescence derivative. The mobile phase used was methanol: water (=80:20 v/v) operated at 0.6 mL/min. The fluorescence was taken with a fluorescence detector (FL type L-2480) at λEc = 365 nm; and λEm=430 nm. The arrows indicate the retention time of the BCPN derivatives. The correlation equation obtained was Y=266716x+2E+6 (R2=0.9441), where Y was the peak area and x was the concentration of BCPN (ppm).
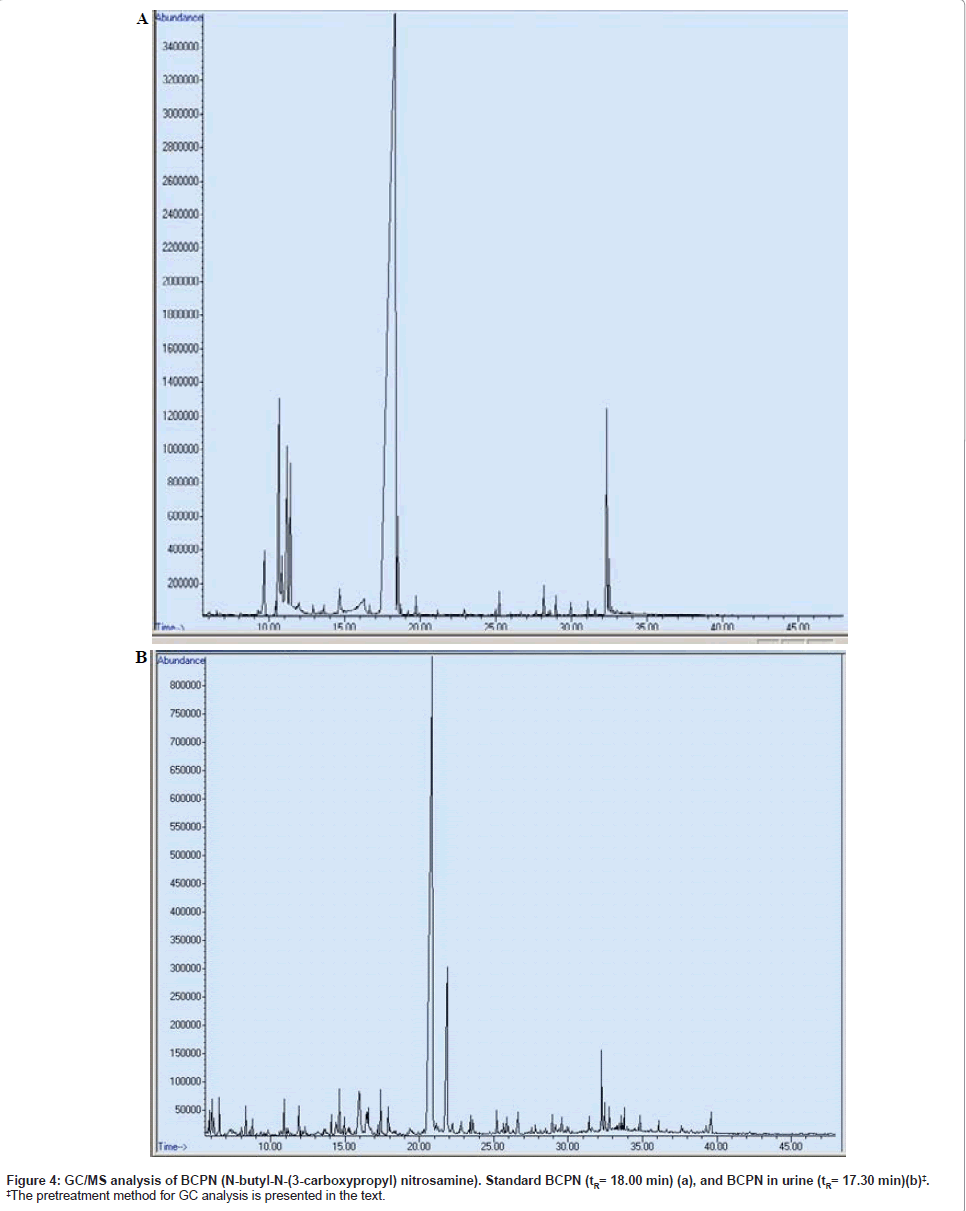
Similar phenomenon was also noted in GC/MS analysis. The tR value was 18.00 min for the reference BCPN, while the urinary sample BCPN shifted to 17.30 min, respectively in duplicate samples (Figure 4). A summarized data of these tR values are listed in Table 1.
| HPLC Analysis | ||
| Sample | Area | Retention timeb (min) |
| Authentic BCPN, ppm 5 10 20 50 100 |
- 176026±185 6605644±1239 10790905±985 14311427±198 28009844±251 |
- 28.48±0.15D 27.59±0.08A 27.43±0.11A 28.00±0.09B 28.32±0.15C |
| Urinary BCPN | 5253622±1023 | 28.23±0.11C |
| GC/MS Analysis | ||
| Authentic BCPN | - | 18.00±0.11B |
| Urinary BCPN | - | 17.30±0.09A |
aTreated as described in section “Materials and methods” of the text.
bDetermination was performed in five replicates.
Different upper case superscripts indicate significant deviation (p<0.05) in either HPLC or GC/MS analysis.
Table 1: Comparison of the retention times between the standard BCPN and the urinary BCPN analyzed by HPLC and GC/MSa.
Thus, the shifts in tR of urinary BCPN were found damping significantly in all samples. There seemed no definite correlation of the tR values of BCPN with its concentration. To avoid such an uncertain effect on the retention time shifts, we suggest the following postulates: i) to avoid a high concentration operation; ii) to install an even and compact packing of the separation column; iii) to operate the mobile phase at a higher and more stable operation pressure, iv) to increase the mobile phase flow at a flow rate as high as possible to abolish the skewed molecular transportation, and v) to avoid a high temperature operation to minimize the unwanted diffusion. The authors who are interested in the theoretical column diffusion and transport during a chromatographic separation are referred to Aldaeus et al. [25]. A more advanced and detail theoretical article had been presented by Balke [26].
Conclusion
Conclusively, the retention time is not absolutely a definite value as often considered in the HPLC or a GC/MS analysis. In reality it may fluctuate depending mainly upon the coexisting molecular interaction, in particular at a high concentration operation, underlying several causes of shifting which can be minimized but not abolished by careful manipulation of the postulates as mentioned.
Acknowledgements
The authors are grateful to the financial support from NSC-96-2320-B-241- 006-MY3 and NSC97-2320-B-469-001-MY3.
References
- Okajima E, Hiramatsu T, Iriya K, Ijuin M, Matsushima S (1975) Effects of sex hormones on development of urinary bladder tumours in rats induced by N-butyl-N-(4-hydroxybutyl) nitrosamine. Urol Res 3: 73-79.
- Okada M, Suzuki E, Hashimoto Y (1976) Carcinogenicity of N-nitrosamines related to N-butyl-N-(4- hydroxybutyl) nitrosamine and N, N-dibutylnitrosamine in ACI/N rats. Gann 67: 825-834.
- Fukushima S, Hirose M, Tsuda H, Shirai T, Hirao K (1976) Histological classification of urinary bladder cancers in rats induced by N-butyl-n-(4- hydroxybutyl)nitrosamine. Gann 67: 81-90.
- lARC (1978) The International Agency for Research on Cancer, Some N-nitroso compounds, IARC Monogr Eval. Carcinog. Risk Chem Hum 17: 51-75.
- Okada M, Ishidate M (1977) Metabolic fate of N-n-butyl-N-(4-hydroxybutyl)- nitrosamine and its analogues, Selective induction of urinary bladder tumours in the rat. Xenobiotica 7: 11-24.
- Ito N, Hiasa Y, Tamai A, Okajima E, Kitamura H (1969) Histogenesis of urinary bladder tumors induced by N-butyl-N-(4-hydroxybutyl) nitrosamine in rats. Gann 60: 401-410.
- Brockmoller J, Cascorbi I, Kerb R, Roots I (1996) Combined analysis of inherited polymorphisms in arylamine N-acetyltransferase 2, glutathione S-transferases M1 and T1, microsomal epoxide hydrolase, and cytochrome P450 enzymes as modulators of bladder cancer risk. Cancer Res 56: 3915-3925.
- Johns LE, Houlston RS (2000) N-acetyl transferase-2 and bladder cancer risk: a meta-analysis.Environ. Mol. Mutagen 36: 221-227.
- Johns LE, Houlston RS (2000) Glutathione S-transferase mu1 (GSTM1) status and bladder cancer risk: a meta-analysis. Mutagenesis 15: 399-404.
- Park SJ, Zhao H, Spitz MR, Grossman HB, Wu X (2003) An association between NQO1 genetic polymorphism and risk of bladder cancer. Mutat Res 536:131-137.
- Giuliani L, Gazzaniga P, Caporuscio F, Ciotti M, Frati L, et al. (2001) Can down-regulation of UDP-glucuronosyltransferases in the urinary bladder tissue impact the risk of chemical carcinogenesis? Int J Cancer 91: 141-143.
- Hashimoto Y, Kitagawa HS (1974) In vitro neoplastic transformation of epithelial cells of rat urinary bladder by nitrosamines. Nature 252: 497-499.
- Airoldi L, Magagnotti C, Bonfanti M, Fanelli R (1990) Alpha-oxidative metabolism of the bladder carcinogensN-nitrosobutyl(4-hydroxybutyl)amine and N-nitrosobutyl(3-carboxypropyl)amine within the rat isolated bladder. Carcinogenesis 11: 1437-1440.
- Airoldi L, Magagnotti C, Bonfanti M, Chiappetta L, Lolli M, et al. (1994) Detection of O6-butyl- and O6-(4-hydroxybutyl)guanine in urothelial and hepatic DNA of rats given the bladder carcinogen N-nitrosobutyl (4-hydroxybutyl)amine. Carcinogenesis 15: 2297-2301.
- Iida K, Itoh K, Kumagai Y, Oyasu R, Hattori K, et al. (2004) Nrf2 is essential for the chemopreventive efficacy of oltipraz against urinary bladder carcinogenesis. Cancer Res 64: 6424-6431.
- Flory PJ (1942) Thermodynamics of high polymer solutions. J Chem Phys 10: 51-61.
- King JW (1995) Determination of the solubility parameter of soybean oil by inverse gas chromatography. Lebensm-Wiss u.-Technol 28: 190-195.
- King JW, List GR (1990) A solution thermodynamic study of soybean oil/solvent systems by inverse gas chromatography. J Am Oil Chem Soc 67: 424-430.
- Gray DG (977) Chromatographic measurements of polymer structure and interactions. Prog Polym Sci 5: 1-60.
- Laub RJ, Pecsok LR (1978) Physicochemical Applications of Gas Chromatography. New York: Wiley-Interscience.
- Mc Glasham ML, Potter DJB (1962) An apparatus for the measurement of the second virial coefficients of vapours; the second viral coefficients of some n-alkanes and of some mixtures of n-alkanes. Proc R Soc Lond A Math Phys Sci 267: 478-500.
- Guggenheim EA, Wormald CJ (1965) Systematic deviations from the principle of corresponding states. J Chem Phys 42: 3775-3780.
- Ozaki K, Sukata T, Yamamoto S, Uwagawa S, Seki T, et al. (1998) High susceptibility of p53 (+/-) knockout mice in N-butyl-N-(4-hydroxybutyl) nitrosamine urinary bladder carcinogenesis and lack of frequent mutation in residual allele. Cancer Res 58: 3806-3811.
- Wada S, Funae Y, Imaoka S, Kawamura M, Kinoshita Y (1985) Rapid assay of N-butyl-N-(3-carboxypropyl)nitrosamine in rat organs and urine by highperformance liquid chromatography after derivatization. Jpn J Cancer Res 76: 192-196.
- Aldaeus F, Thewalim Y, Colmsjo A (2009) Prediction of retention times and peak widths in temperature-programmed gas chromatography using the finite element method. J Chromatogr A 1216: 134-139.
- Balke ST (1984) Quantitative Column Liquid Chromatography - a Survey of Chromatometric Methods. J Chromatography Library vol. 29 (Xerox Research Centre of Canada, Mississauga, Ontario L5K2L1, Canada Elsevier, Amsterdam Oxford-New York-Tokyo).
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 15171
- [From(publication date):
January-2011 - Jan 05, 2025] - Breakdown by view type
- HTML page views : 10720
- PDF downloads : 4451